- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика волновых явлений презентация
Содержание
- 1. Физика волновых явлений
- 2. Волны - процесс распространения колебаний в пространстве.
- 3. Бегущая волна Предположим поперечное сечение стержня не
- 4. Остальные сечения кол. вынужд. колеб. А всех колебаний одинакова. Потери не учитываются
- 5. Длина волны Расстояние, на которое
- 6. 1
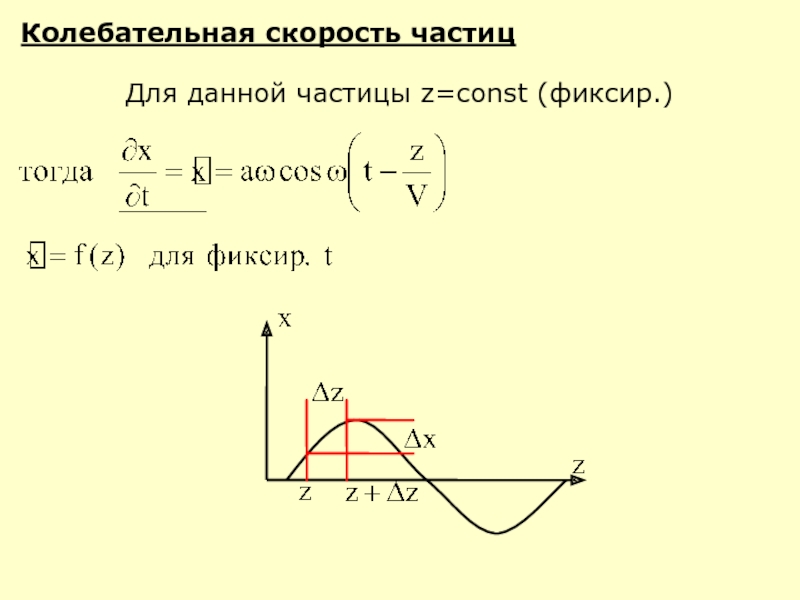
- 7. Колебательная скорость частиц Для данной частицы z=const (фиксир.)
- 8. Относительная деформация и напряжение в среде при
- 9. Закон Гука - механическая мера внутренних
- 10. Уравнение Даламбера
- 11. Надо найти равнодействующую
- 12. Выражаем через
- 13. Резюме: Единственное предположение Уравнение Даламбера справедливо
- 14. Уравнение (3.1) удобно для расчета V при
- 15. Скорость распространения упругой волны в газе Теплообмен
- 16. Энергия, переносимая волной
- 17. Потенциальная энергия Упругий образец длиной l растягивается
- 18. Кинетическая энергия волны Рассматривается плоская волна,
- 19. Pпот=Pкин Для любой точки бегущей волны мгновенные
- 20. Явная зависимость мгновенного значения плотности энергии от
- 21. Плотность потока энергии (вектор Умова) Энергия через
- 22. Волновое (акустическое сопротивление среды) Уравнение
- 23. Из (4) следует, что отношение совершающих гармоническое
- 24. Уравнение сферической волны
- 25. В изотропной среде на расстоянии r от
- 26. 3. Лучи (направления распространения колебательной энергии) в
- 27. Зависимость амплитуды колебаний от расстояния Если в
- 28. примем уcловие: наименьшее расстояние от источника колебаний,
- 29. При распространении сферической волны между колебаниями
- 30. Среднее значение J:
- 31. Стоячие волны
- 32. Рассмотрим волновой режим в системе, линейные размеры
- 33. Волна распространяется в направлении оси z Суперпозиция
- 34. Рассмотрим графики зависимости x=x(z)
- 35. В отличие от бегущей волны, в которой
- 36. Характерные особенности стоячих волн 1. Амплитуда колебаний
- 37. 3. Колебания точек, заключённых между двумя узлами,
- 38. 5. Стоячая волна напряжений:
- 39. 6.Стоячая волна не переносит энергии. Действительно, мгновенное
- 40. Акустика
- 41. 1. Звуковые колебания и их распространение Звук
- 42. Звуковые впечатления: - высота – зависит
- 43. Порог болевого ощущения: интенс Субъективная характеристика –
- 44. 2. Скорость распространения упругих волн в газе.
- 45. Подст в (3) Из ур-я Клапейрона-Менделеева И окончательно:
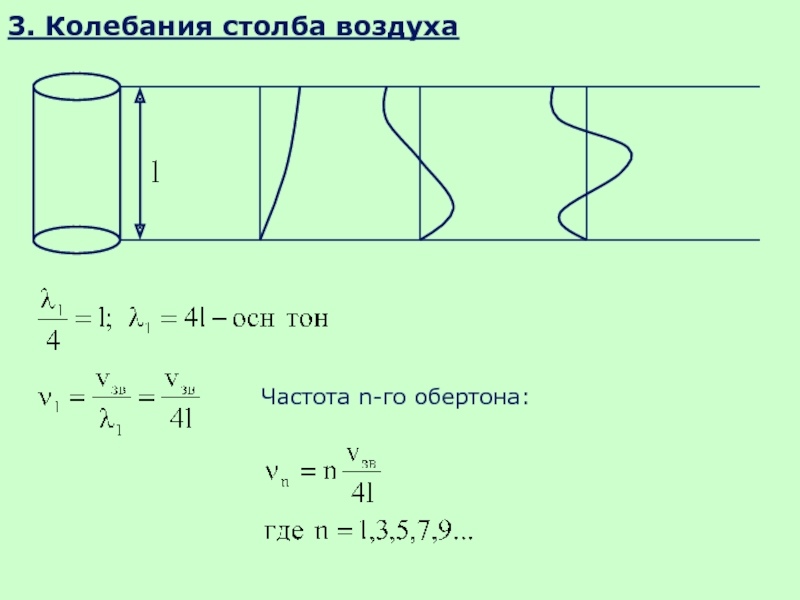
- 46. 3. Колебания столба воздуха Частота n-го обертона:
- 47. Эффект Доплера
- 48. (австриец Христиан Доплер (1803-1853)) Эффект Доплера –
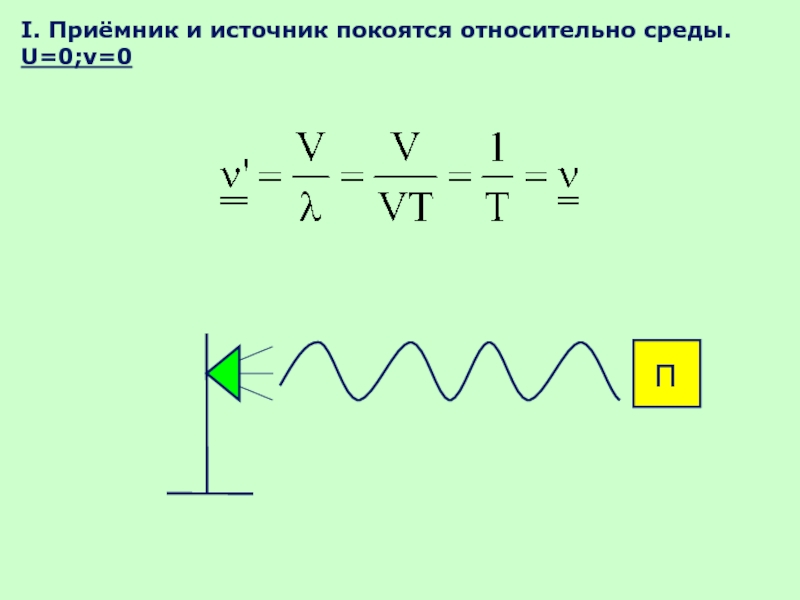
- 49. I. Приёмник и источник покоятся относительно среды. U=0;v=0 П
- 50. II. Приёмник движется относительно среды со скоростью
- 51. III. Источник движется, приёмник покоится (U=U;v=0)
- 52. IV. Источник и приёмник перемещаются одновременно (U=0;
- 53. Интерференция волн Если от источника колебаний волны
- 54. Приёмник под воздействием одной первой волны совершал
- 55. Аналогично, для интерференционного ослабления необходимо: Таким образом:
- 56. Отражение волн Проникновение волн через границу Условие:
- 57. Так как площадь, на которую падает волна,
- 58. Следует обратить внимание на появление дополнительных (по
- 59. Примем на границе z=0, тогда: Потому,
- 60. Используя введённые обозначения, уравнения (12) – (15)
- 61. 1. определение Вычитая (19) из (17) получаем:
- 62. 1. определение Вычитая (18) из (16) получаем:
- 63. 1. Определение R Выразив
- 64. Принцип Гюйгенса Каждая точка поверхности волны должна
- 65. Примеры применения принципа Гюйгенса 1. Отражение плоской
- 66. 1. Преломление плоской волны через плоскую границу
- 67. В случае упругих волн: В случае электромагнитных
- 68. Электромагнитные волны
- 69. Максвелл, Джеймс Клерк В 1860—1865 Максвелл создал
- 71. Уравнения Максвелла (собираем) I
- 72. Приложение к ур-ниям Максвелла в дифференциальной форме
- 73. Шкала ЭМВ ЧастотаГц Длина волны, см Электромагнитные волны
- 74. Видимый свет Электромагнитные волны
- 75. I. Е колеблется H; ЭМВ –
- 76. Электромагнитные волны
- 77. Поперечность ЭМВ Согл (1) Т.е. вдоль z не меняется и по t Электромагнитные волны
- 78. Волновое уравнение ЭМВ (Даламбера) Уравнения Максвелла
- 79. Электромагнитные волны Скорость ЭМВ Ранее для упругих
- 80. Электромагнитные волны Для ЭМВ обозначим
- 81. Электромагнитные волны В случае плоско-поляризованой монохроматической
- 82. Электромагнитные волны С учётом (13) из
- 83. Электромагнитные волны Итак ?В распространяющейся
Слайд 2Волны - процесс распространения колебаний в пространстве. Обусловлен наличием связей
Механизм –
Упругие (механ.) волны ?
? Между частицами среды действуют действуют силы упругой связи
Перпендикулярно направлению распространения волны – поперечные волны.
2. Вдоль направления распространения волны – продольные.
Поперечные когда упругая деформация сдвига.
Продольные – упругая деформация сжатия и растяжения.
Слайд 3Бегущая волна
Предположим поперечное сечение стержня не деформируется. Оно колеблется перпендикулярно (сдвиг)
Геометрическое место точек, колеблющихся в одинаковой фазе, называется поверхностью волны
(Затухание не учитывается)
Z=0
Z
Z
Слайд 5Длина волны
Расстояние, на которое распространяется волна за один период колебаний
Подставим (5) в (4)=>
Уравнение бегущей волны ?
Из (1) и (6) отставание по фазе точки с координатой z
Разность фаз
- это кратчайшее расстояние между точками, колеблющимися в одинаковых фазах
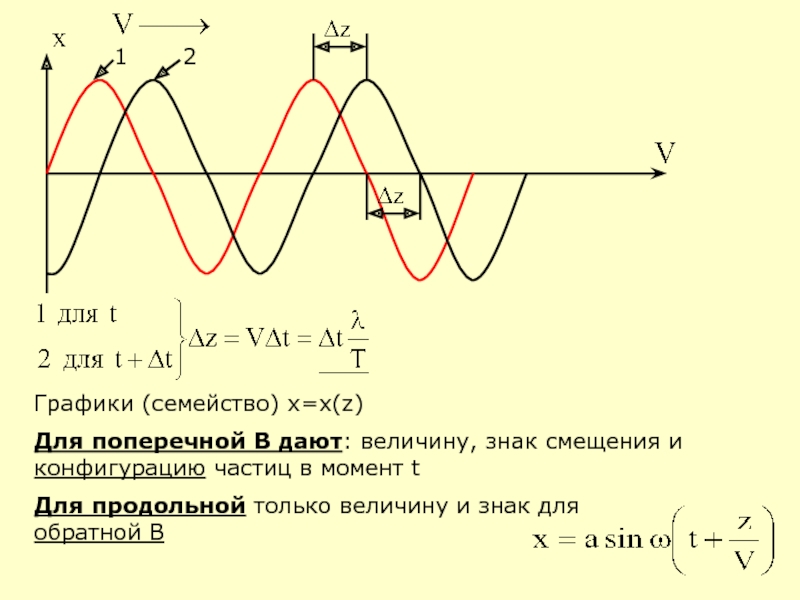
Слайд 6
1 2
Графики (семейство) x=x(z)
Для поперечной B дают: величину,
Для продольной только величину и знак для обратной B
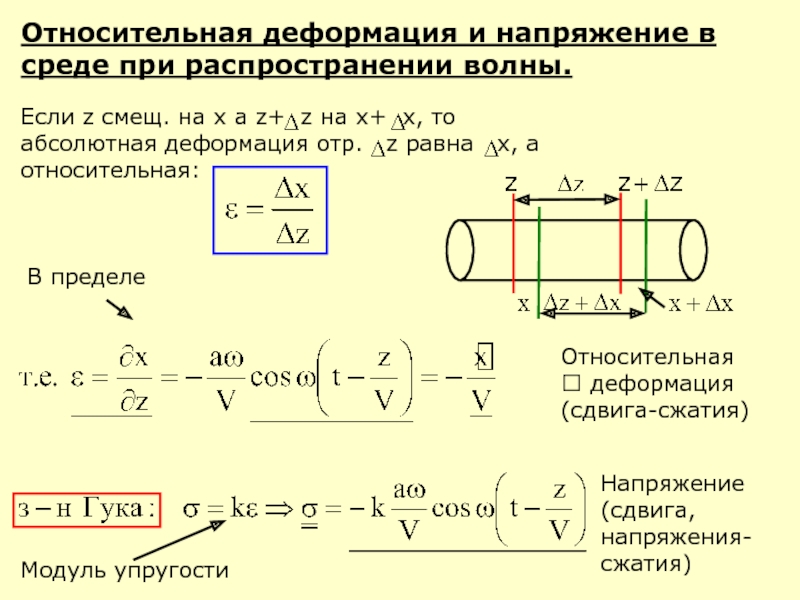
Слайд 8Относительная деформация и напряжение в среде при распространении волны.
Если z смещ.
В пределе
Относительная ? деформация (сдвига-сжатия)
Модуль упругости
Напряжение (сдвига, напряжения-сжатия)
Слайд 9
Закон Гука
- механическая мера внутренних сил при деформации материала.
-модуль упругости
k
Модуль сдвига
Модуль Юнга Е (прод.)
Составляющие деформации в данной точке являются линейными и однородными функциями составляющих напряжения.
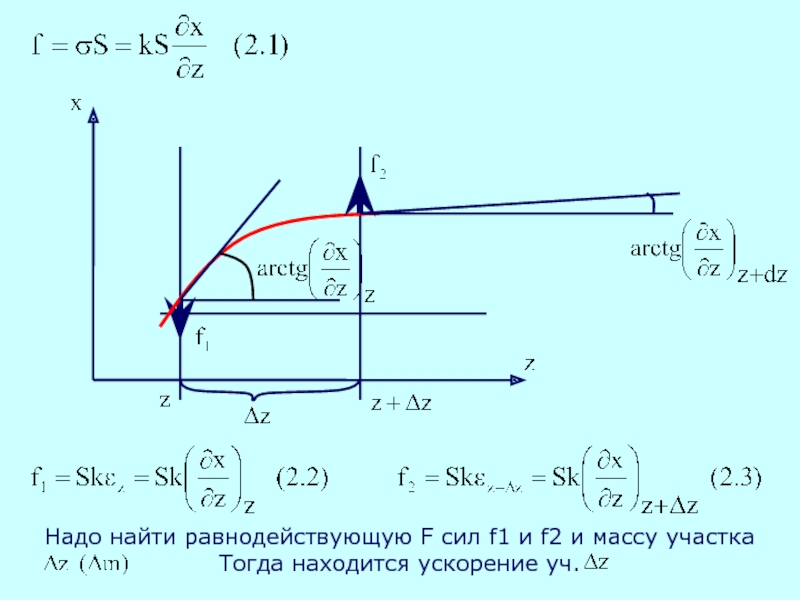
Слайд 12
Выражаем через и приращение деформации
Ускорение, приобретаемое стержнем
Уравнение Даламбера
Слайд 13
Резюме:
Единственное предположение
Уравнение Даламбера справедливо для распространения движения любого характера в среде
Волновому уравнению удовлетворяют бегущие волны
а также вообще периодический сигнал, смещение в котором есть
Скорость распространения упругих волн
Слайд 14Уравнение (3.1) удобно для расчета V при известных и
Скорость
Где: Е – модуль Юнга
G – модуль сдвига.
Скорость распространения упругой волны в жидкости
В жидкости волны продольные
Коэф. Сжимаемости жидкости
Слайд 15Скорость распространения упругой волны в газе
Теплообмен между сгущ и разряж не
Для расчёта V надо найти E исходя из 3.10 и уравнения адиабаты
Из уравнения Клапейрона-Менделеева:
Похоже на среднеквадр скорость молекул в газе
Слайд 17Потенциальная энергия
Упругий образец длиной l растягивается силой f. Во всём образце
S – поперечное сечение. Под действием силы f образуется удлинение
Работа растяжения упругого тела=полной потенциальной энергии упругой деформации, накопленной в теле
Удельная энергия, запасённая в единице объёма – плотность энергии
(4.2) полученное при однородном напряжённом состоянии пригодно и для неоднородного (бегущие волны), когда V настолько мало, что напряжённое состояние в различных его точках можно считать одинаковым. (4.2) даёт мгновенные значения
Слайд 18
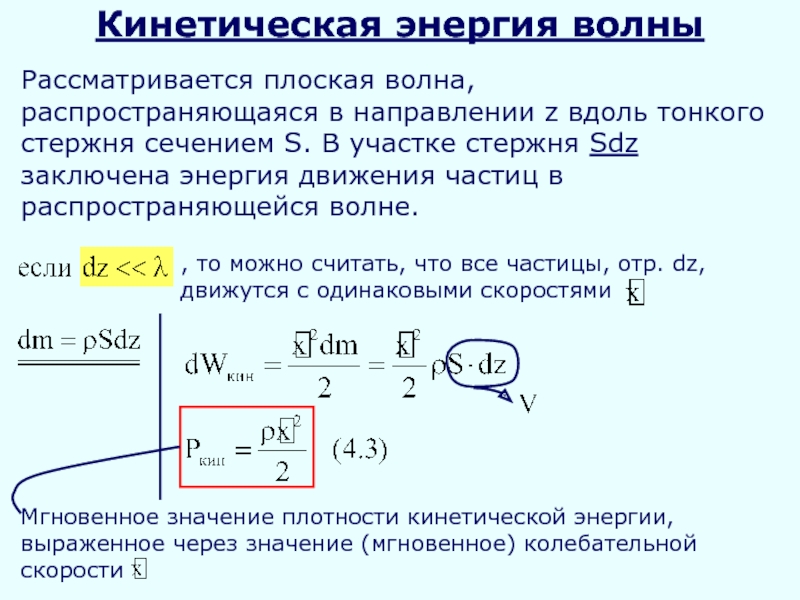
Кинетическая энергия волны
Рассматривается плоская волна, распространяющаяся в направлении z вдоль тонкого
, то можно считать, что все частицы, отр. dz, движутся с одинаковыми скоростями
Мгновенное значение плотности кинетической энергии, выраженное через значение (мгновенное) колебательной скорости
Слайд 19Pпот=Pкин
Для любой точки бегущей волны мгновенные значения плотности потенциальной и кинетической
Докажем:
Мгновенное значение плотности полной энергии
Слайд 20Явная зависимость мгновенного значения плотности энергии от координат и времени
См (4.5)
Согласно (4.6) при распространении В происходит перенос энергии. Скорость переноса энергии зависит от скорости передачи смещения, колебательной скор. частиц и деформации в среде, вследствие некоторой связи энергии с этими величинами.
Частота колебания Р= удвоенной частоте колебаний
Слайд 21Плотность потока энергии (вектор Умова)
Энергия через данное сечение за единицу времени
Плотность
Слайд 22Волновое (акустическое сопротивление среды)
Уравнение
среде при прохождении волны, со скоростью колеблющейся частицы.
Коэффициент пропорциональности , связывающий значение напряжения в данной точке среды с мгновенным значением скорости этой точки, называется волновым (звуковым или акустическим) сопротивлением среды
Волновое сопротивление – весьма важная характеристика среды: при переходе волны из одной среды в другую или при отражении волны от границы двух сред, значение коэффициентов отражения и проникновения целиком определяются отношением волновых сопротивлений граничащих сред.
Слайд 23Из (4) следует, что отношение совершающих гармоническое колебание напряжения
Неизменность отношения мгновенных значений и имеет место только в плоской волне. Здесь всегда справедливы следующие отношения для амплитудных и действующих значений этих величин:
Слайд 25В изотропной среде на расстоянии r от источника
- обратить внимание на
1. Колебания каждой точки отстают по фазе от колебаний предыдущей точки.
Тогда разность фаз между ними:
2. Поверхность волны (Г.М.Т., колеблющихся в одинаковых фазах) определяется (2) и является сферической поверхностью.
Такие волны называются сферическими.
Слайд 263. Лучи (направления распространения колебательной энергии) в изотропной среде перпендикулярны поверхности
поверхности волны и лучи образуют два ортогональных семейства
луч
поверхностьволны
4. Длина сферической волны – кратчайшее расстояние (по лучу) между двумя точками, колеблющимися в одинаковых фазах.
5. Амплитуда колебаний точек среды – убывающая функция r, т.к
колебание, по мере удаления от источника, распространяется на всё большее количество точек ?
интенсивность волны (плотность потока энергии) уменьшается с удалением от источника.
Слайд 27Зависимость амплитуды колебаний от расстояния
Если в среде нет поглощения:
из (3) следует
тогда
Слайд 28примем уcловие: наименьшее расстояние от источника колебаний, на котором источник можно
амплитуда на этом расстоянии
тогда:
Слайд 29
При распространении сферической волны между колебаниями напряжения в
Колебание напряжения может быть представлено как сумма двух колебаний:
Одного в той же фазе, что и скорость и другого, сдвинутого по фазе на 900
Слайд 32Рассмотрим волновой режим в системе, линейные размеры которой равны небольшому числу
Стоячая волна –
результат суперпозиции падающей и отражённой волн
Среда - струна, воздух - резонатор
Слайд 33Волна распространяется в направлении оси z
Суперпозиция этих двух волн даёт:
Полученное уравнение
Примем условие: имеет место полное отражение, т.е. колебательная энергия не передаётся в соседнюю среду.
При этом амплитуда отражённой волны = амплитуде падающей
Sin α+ Sin β = 2sin((α+β)/2)cos((α-β)/2)
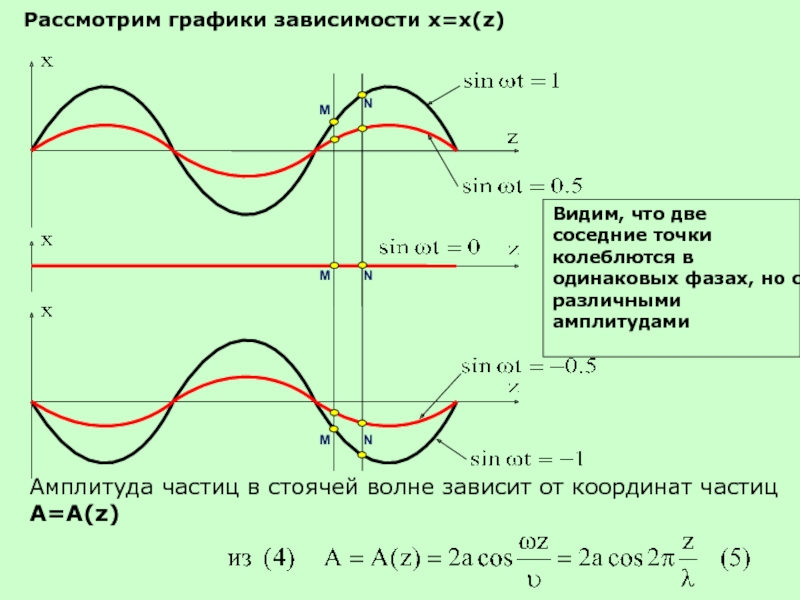
Слайд 34Рассмотрим графики зависимости x=x(z)
Видим, что две соседние точки колеблются в одинаковых
Амплитуда частиц в стоячей волне зависит от координат частиц A=A(z)
M
M
M
N
N
N
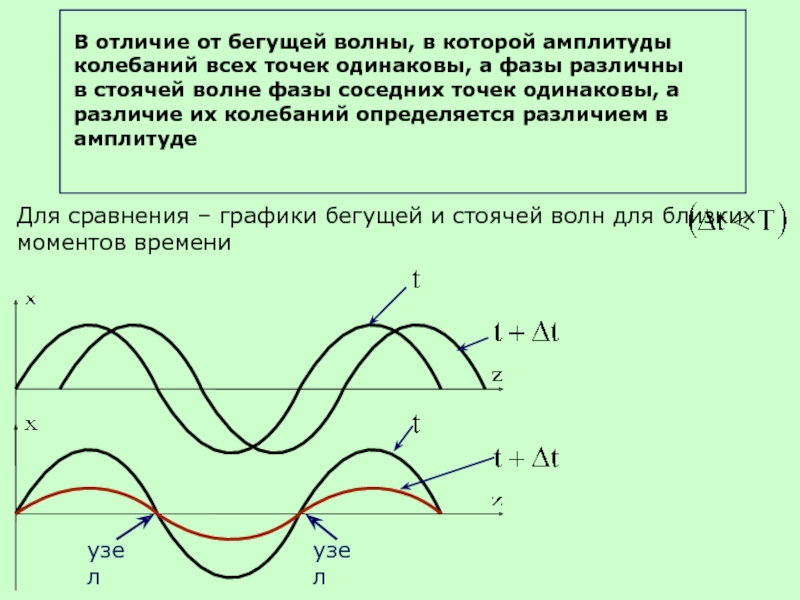
Слайд 35В отличие от бегущей волны, в которой амплитуды колебаний всех точек
в стоячей волне фазы соседних точек одинаковы, а различие их колебаний определяется различием в амплитуде
Для сравнения – графики бегущей и стоячей волн для близких моментов времени
узел
узел
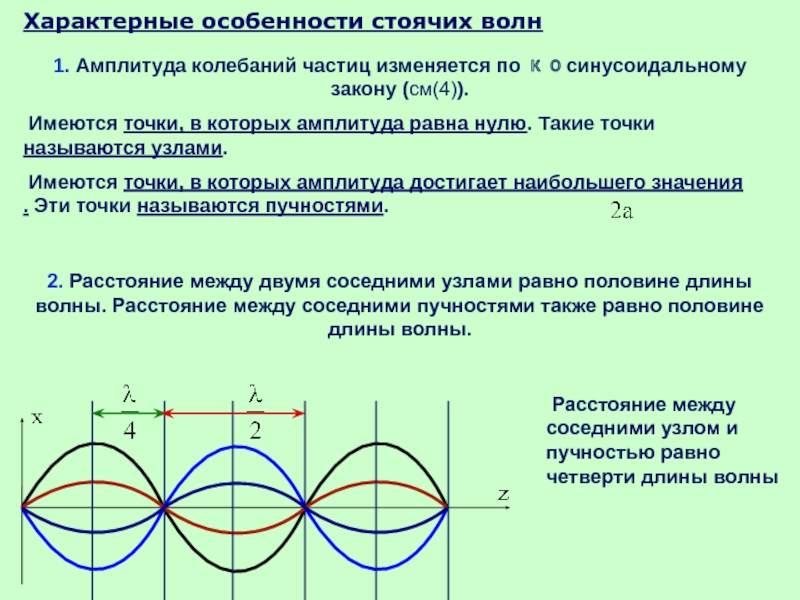
Слайд 36Характерные особенности стоячих волн
1. Амплитуда колебаний частиц изменяется по косинусоидальному закону
Имеются точки, в которых амплитуда равна нулю. Такие точки называются узлами.
Имеются точки, в которых амплитуда достигает наибольшего значения . Эти точки называются пучностями.
2. Расстояние между двумя соседними узлами равно половине длины волны. Расстояние между соседними пучностями также равно половине длины волны.
Расстояние между соседними узлом и пучностью равно четверти длины волны
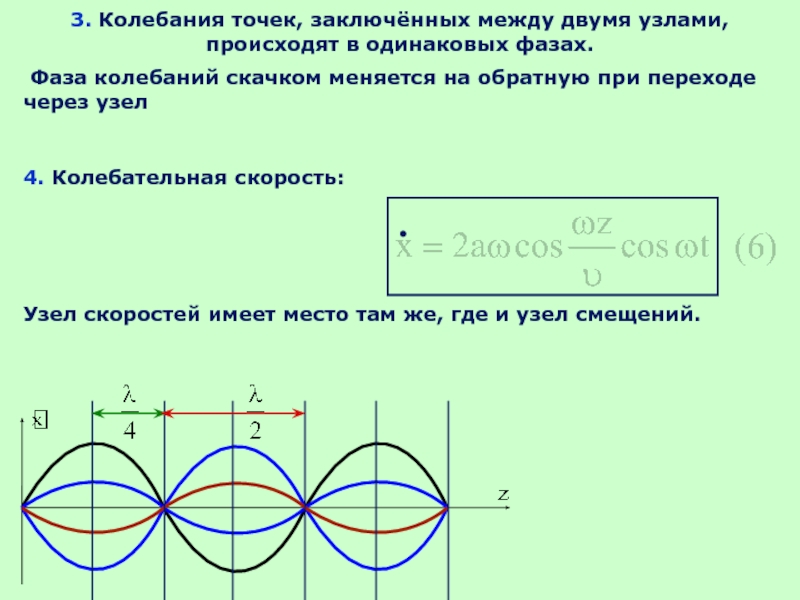
Слайд 373. Колебания точек, заключённых между двумя узлами, происходят в одинаковых фазах.
4. Колебательная скорость:
Узел скоростей имеет место там же, где и узел смещений.
Слайд 38
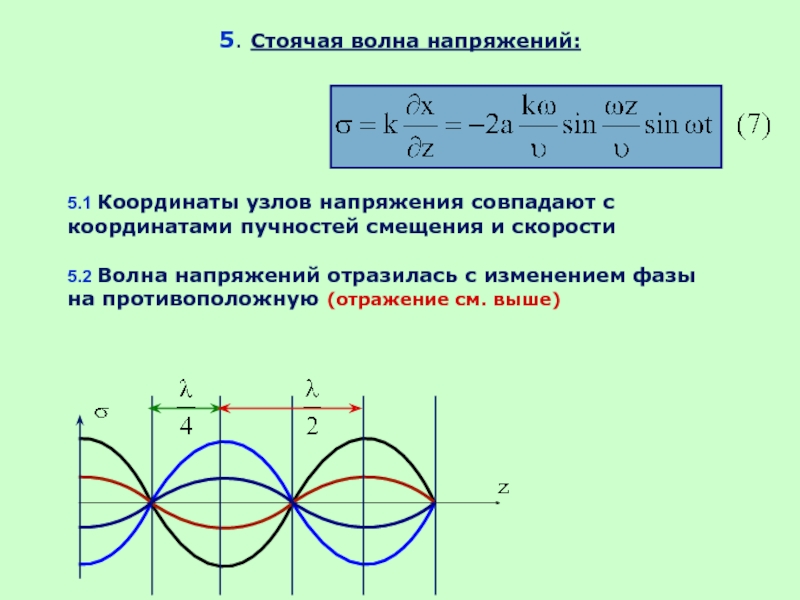
5. Стоячая волна напряжений:
5.1 Координаты узлов напряжения совпадают с координатами пучностей
5.2 Волна напряжений отразилась с изменением фазы на противоположную (отражение см. выше)
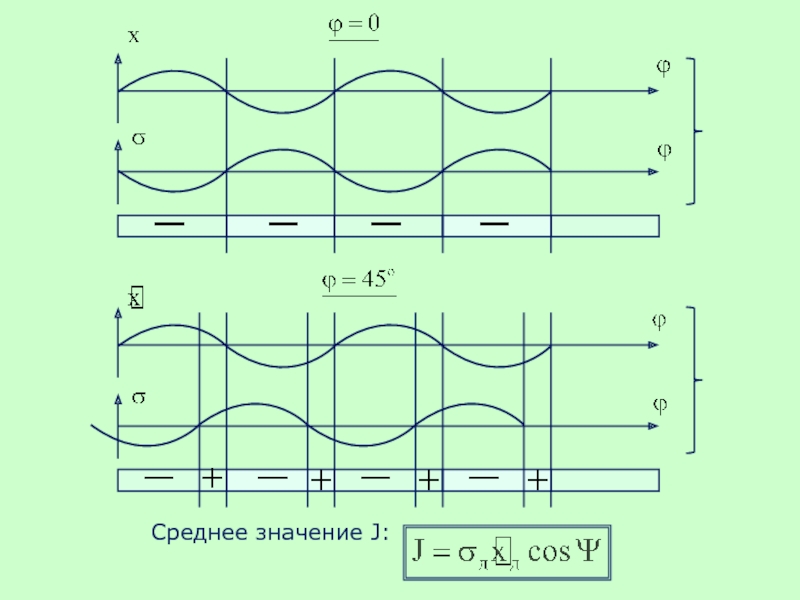
Слайд 396.Стоячая волна не переносит энергии. Действительно, мгновенное значение плотности потока энергии
Среднее значение потока энергии J равно нулю
При выводе (4) амплитуды падающей и отражённой волн были одинаковыми (при полном отражении)
При частичном переходе энергии максимальная амплитуда
а не , как в (5)
Такая волна переносит энергию, передаваемую в соседнюю среду.
ψ
В стоячей волне ψ = 90о и J = 0
.
Слайд 411. Звуковые колебания и их распространение
Звук – это продольные упругие колебания
Воспринимается от 16 Гц до 20000 Гц. ? связано с физиологией человека.
f>20000 Гц – ультразвук; f<16 Гц – инфразвук.
В физике (независимо от f) звуковые колеб – упр колебан распр в среде.
Объект. характеристики: - интенсивность колебаний - плотность потока энергии - скорость распространения колебаний
В обиходе: - сила звука - скорость звука
Слайд 42
Звуковые впечатления: - высота – зависит от частоты - тембр – обертоны -
1я 2я 3я
Ля: 440 880 1760 Гц.
Порог слышимости – min интенсивность волны, вызывающая звуковое ощущение
Наиболее слышимы 1000-4000 Гц ? порог слыш-ти
При других f он лежит выше
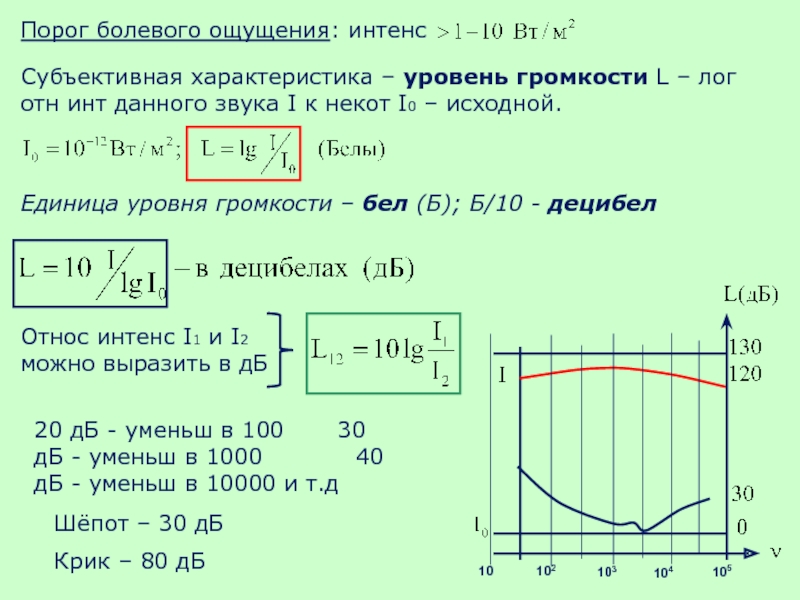
Слайд 43Порог болевого ощущения: интенс
Субъективная характеристика – уровень громкости L – лог
Единица уровня громкости – бел (Б); Б/10 - децибел
Относ интенс I1 и I2 можно выразить в дБ
20 дБ - уменьш в 100 30 дБ - уменьш в 1000 40 дБ - уменьш в 10000 и т.д
Шёпот – 30 дБ
Крик – 80 дБ
10
102
103
104
105
Слайд 442. Скорость распространения упругих волн в газе.
Скорость распространения упр волн в
Модуль Юнга
Плотность среды
По определению для упругого стержня
Для объёма объёмн деформ
Полаг беск. малые dP и dV. Увел dP ? уменьш dV (отриц)
Перепишем (2) ?
Звук колеб происх так быстро, что теплов обмен между сгущ и разреж произ не успевает – т.е.происх адиабатически
Слайд 48(австриец Христиан Доплер (1803-1853))
Эффект Доплера – изменение частоты распространяющихся в среде
V – скорость распространяющихся колебаний в среде
U – скорость источника относительно среды
v – скорость приёмника относительно среды
сближение п и (+) (V,U)
удаление п и (-) (V,U)
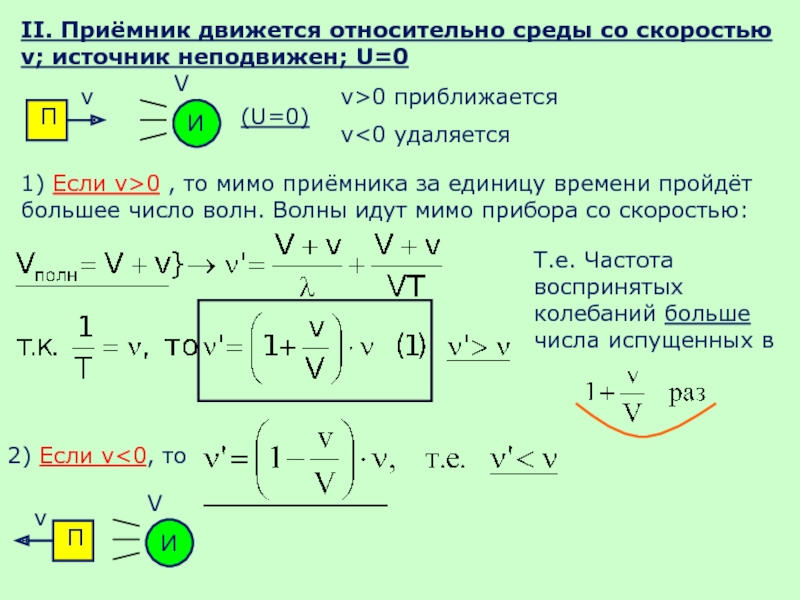
Слайд 50II. Приёмник движется относительно среды со скоростью v; источник неподвижен; U=0
П
И
v
V
(U=0)
v>0
v<0 удаляется
1) Если v>0 , то мимо приёмника за единицу времени пройдёт большее число волн. Волны идут мимо прибора со скоростью:
Т.е. Частота воспринятых колебаний больше числа испущенных в
2) Если v<0, то
П
И
v
V
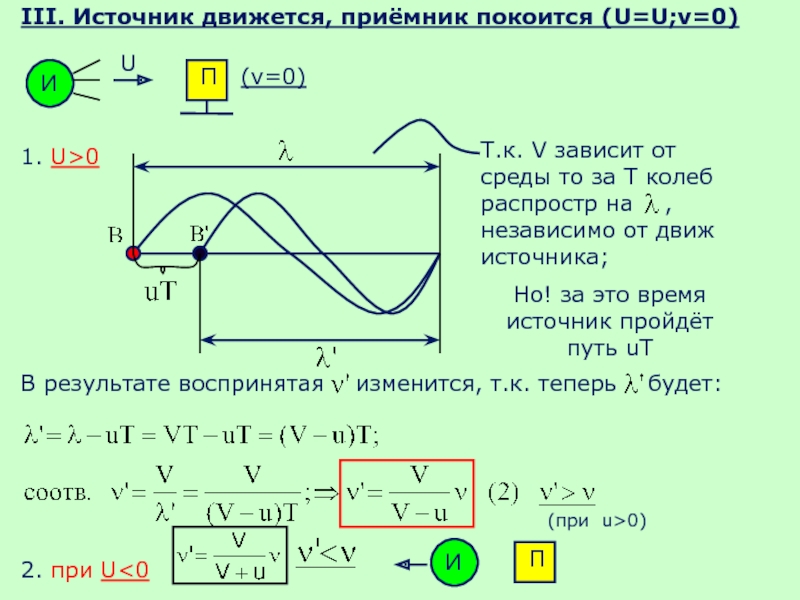
Слайд 51III. Источник движется, приёмник покоится (U=U;v=0)
П
И
(v=0)
U
1. U>0
Т.к. V зависит от среды
Но! за это время источник пройдёт путь uT
В результате воспринятая изменится, т.к. теперь будет:
2. при U<0
(при u>0)
П
И
Слайд 52IV. Источник и приёмник перемещаются одновременно (U=0; v=0)
Вследствие движ источника
Вследствие движ
Вследствие обеих причин:
Если v и U направить под углом, то следует брать их составляющие на прямую, соединяющую источник и приёмник.
Слайд 53Интерференция волн
Если от источника колебаний волны доходят до приёмника двумя различными
При одинаковых направлениях слагаемых колебаний амплитуда и энергия результирующего колебания:
При сложении одинаково направленных колебаний равных частот энергия результирующего колебания не равна сумме энергий слагаемых колебаний, совершающихся порознь
Интерференция волн – усиление или ослабление энергии результирующего колебания в зависимости от разности фаз слагаемых колебаний
При сложении взаимно перпендикулярных колебаний интерференции нет, т.к. при любых энергия
Слайд 54Приёмник под воздействием одной первой волны совершал бы колебания, следующие уравнению:
a
Разность фаз колебаний приёмника под воздействием одного и другого колебаний:
Разность расстояний , которые проходят волны от источников до приёмника, называется разностью хода волн
Интерференционное усиление, согласно (1), имеет место при условии
отсюда
Слайд 55Аналогично, для интерференционного ослабления необходимо:
Таким образом:
Интерференционное усиление имеет место, если разность
Интерференционное ослабление имеет место, если разность хода лучей равна нечётному числу длин полуволн
Слайд 56Отражение волн
Проникновение волн через границу
Условие: волна распространяется вдоль оси z, перпендикулярной
Волновое сопротивление первой среды (в ней распространяются подающая и отражённая волны)
Волновое сопротивление второй среды (в ней распространяется проникшая через границу раздела волна)
Отношение волновых сопротивлений сред
Амплитуды колебаний частиц падающей, отражённой и преломлённой волн соответственно
Амплитуды колебательной скорости частиц
Амплитуды напряжений среды, вызванных падающей, отражённой и прошедшей через границу волн соответственно
Коэффициент отражения
Коэффициент проникновения
Слайд 57Так как площадь, на которую падает волна, равна площади, от которой
Так как падающая и отражённая волны распространяются в одной и той же среде, то:
Падающая и проникшая через границу волны распространяются в разных средах, поэтому:
Слайд 58Следует обратить внимание на появление дополнительных (по сравнению с падающей волной)
На границе раздела двух сред выполняется
условие непрерывности: в природе не бывает бесконечно больших перепадов смещений, колебательных скоростей частиц и напряжений
Слайд 59Примем на границе z=0, тогда:
Потому, что волна напряжений должна отразиться от
Если в (10) подставить знак +, то оно окажется несовместимым с (9)
Из (10) после подстановки следует:
По (9) скобки в л.ч. и п.ч. уравнения (11) равны, поэтому , что не соответствует условию
Из (9) и (10), справедливых в любой момент времени, можно получить:
Слайд 60Используя введённые обозначения, уравнения (12) – (15) можно представить в виде:
Система
Слайд 611. определение
Вычитая (19) из (17) получаем:
Для определения знака
Волна проникает во вторую среду без изменения фазы, т.е. в отношении фазы преломления волна является продолжением предыдущей.
Слайд 621. определение
Вычитая (18) из (16) получаем:
1. При отражении от среды с
2. При отражении от среды с большим акустическим сопротивлением волна смещений и волна колебательных скоростей частиц изменяют фазу на ; волна напряжений не изменяет фазу
Слайд 631. Определение R
Выразив из (16) и подставив его
Коэффициенты отражения от границы данных двух сред одинаковы как для волны, падающей на границу из первой среды, так и для волны , падающей на границу из второй среды
1. Определение T
Выразив из (16) и подставив его в (18), получим:
По закону сохранения энергии поток энергии падающей волны равен сумме потоков энергии отражённой и проникшей во вторую среду волн. Поэтому должно иметь место равенство:
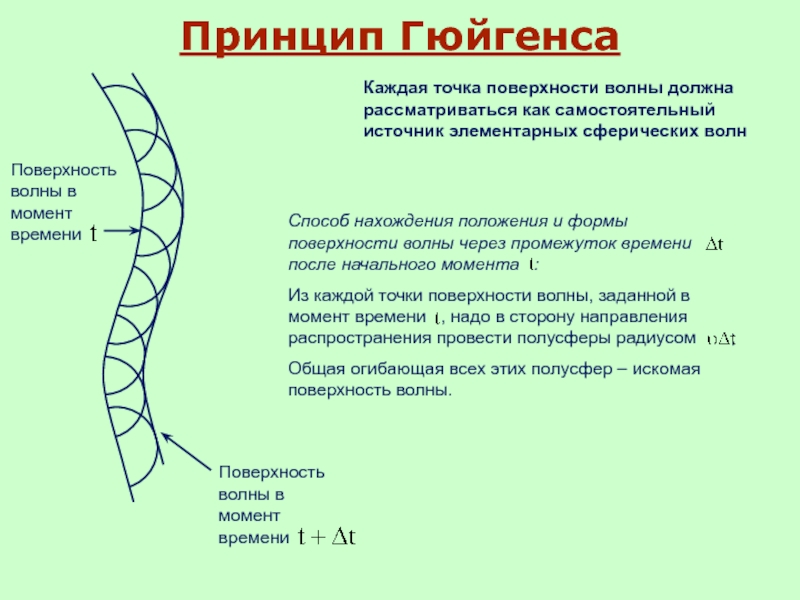
Слайд 64Принцип Гюйгенса
Каждая точка поверхности волны должна рассматриваться как самостоятельный источник элементарных
Поверхность волны в момент времени
Поверхность волны в момент времени
Способ нахождения положения и формы поверхности волны через промежуток времени после начального момента :
Из каждой точки поверхности волны, заданной в момент времени , надо в сторону направления распространения провести полусферы радиусом ;
Общая огибающая всех этих полусфер – искомая поверхность волны.
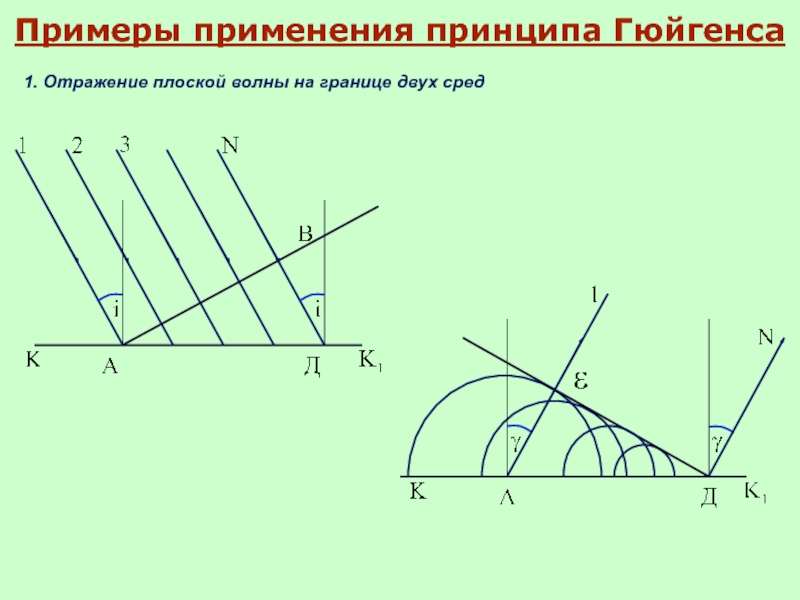
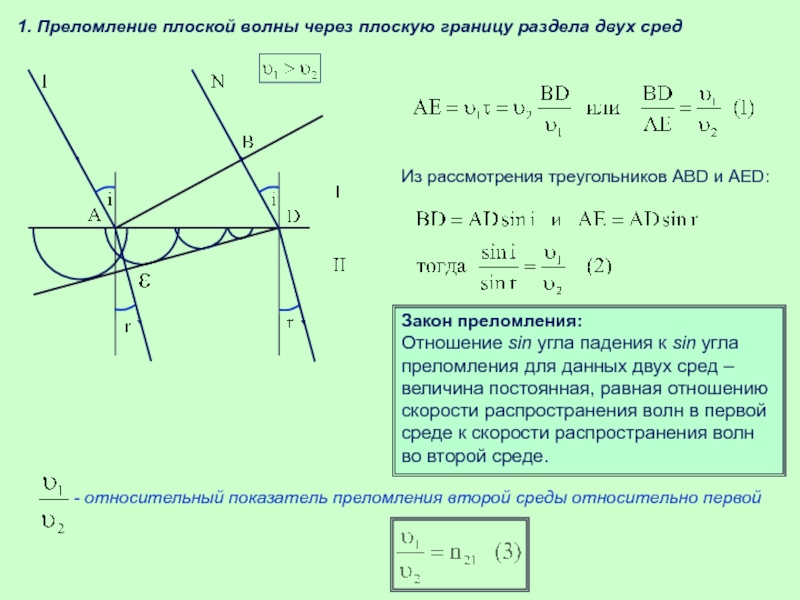
Слайд 661. Преломление плоской волны через плоскую границу раздела двух сред
Из рассмотрения
Закон преломления:
Отношение sin угла падения к sin угла преломления для данных двух сред – величина постоянная, равная отношению скорости распространения волн в первой среде к скорости распространения волн во второй среде.
- относительный показатель преломления второй среды относительно первой
Слайд 67В случае упругих волн:
В случае электромагнитных волн:
Для всех не ферромагнитных сред
Показатель преломления среды относительно вакуума, где принимает вид:
При переходе волны из одной среды в другую, частота колебаний не изменяется.
Так как скорости распространения в различных средах различны, то длина волны при переходе из одной среды в другую изменяется.
Слайд 69Максвелл, Джеймс Клерк
В 1860—1865 Максвелл создал теорию электромагнитного поля, которую сформулировал
В 1861г. он обнаружил, что свет — это разновидность электромагнитных волн.
Д.К.Максвелл (1831-1879) - великий английский учёный, создатель теории электромагнетизма.
Максвелл также создал Создал кинетическую теорию газов (1859г.) и вывел соотношение для распределения цастиц газов по скоростям, получившего название распределения Максвелла.
Слайд 70
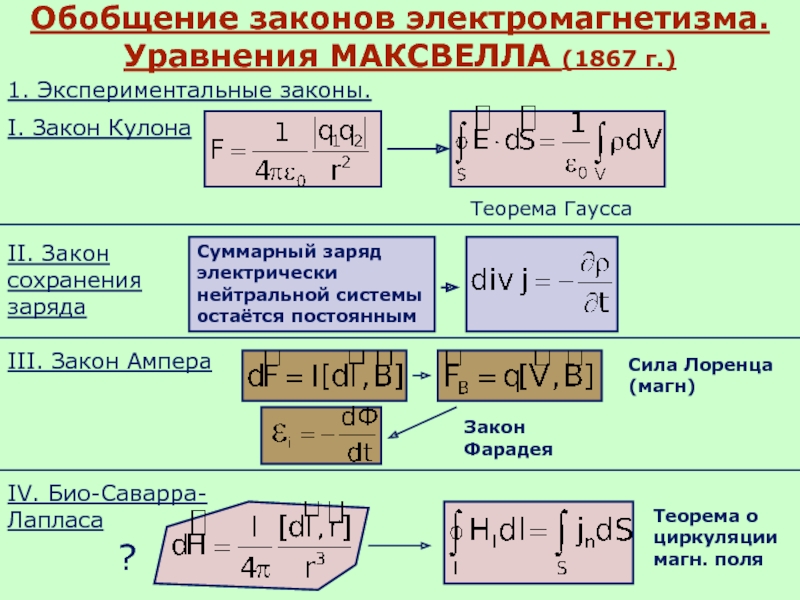
Обобщение законов электромагнетизма. Уравнения МАКСВЕЛЛА (1867 г.)
1. Экспериментальные законы.
I. Закон Кулона
Теорема
II. Закон сохранения заряда
Суммарный заряд электрически нейтральной системы остаётся постоянным
III. Закон Ампера
Сила Лоренца (магн)
Закон Фарадея
IV. Био-Саварра-Лапласа
?
Теорема о циркуляции магн. поля
Слайд 71
Уравнения Максвелла (собираем)
I
II
Интегральная форма Дифференциальная форма
Материальные уравнения
Слайд 72Приложение к ур-ниям Максвелла в дифференциальной форме
Теоремы Стокса и Остроградского-Гаусса
Т. Стокса
Т.
где
Слайд 75I. Е колеблется H; ЭМВ – поперечная волна
Модель: E(z,t) т.е.
Ур-я Максвелла
Электромагнитные волны
Слайд 78
Волновое уравнение ЭМВ (Даламбера)
Уравнения Максвелла для плоско – поляризованной волны сводятся:
Уравнение
ЭМВ
Электромагнитные волны
Слайд 79Электромагнитные волны
Скорость ЭМВ
Ранее для упругих колебаний было показано:
Для бегущей волны v
Сравнивая (7) и (5), (6) видим:
Слайд 80
Электромагнитные волны
Для ЭМВ обозначим vсреды=Сср; vвак=C – скорость света (ЭМВ) в
В Си
Слайд 81
Электромагнитные волны
В случае плоско-поляризованой монохроматической волны ур-ям (5), (6) соотв решение:
Задача:
Сгласно (4)
синфазность
Тождеств. вып. (12) (т.е. при любых коорд и в любой момент)
Возможно только при
В бегущей ЭМВ Е и Н колеблются в одинаковых фазах
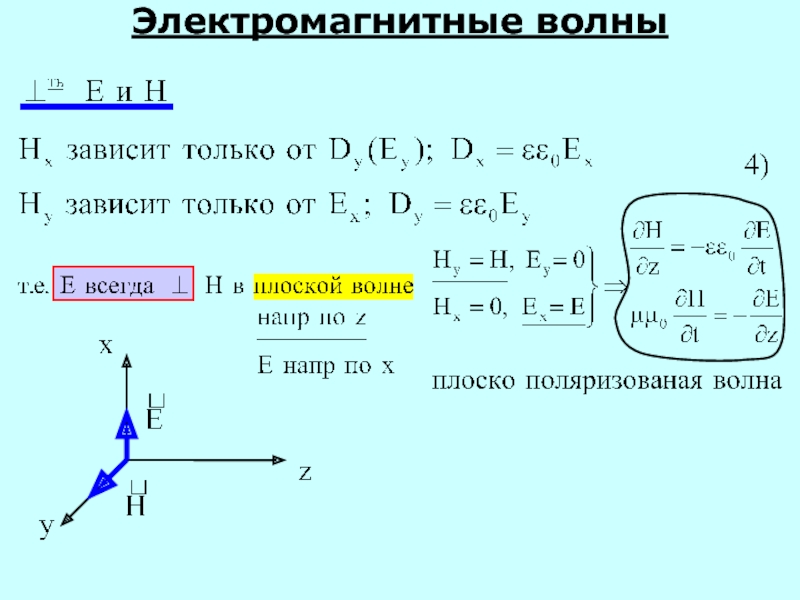
Слайд 82
Электромагнитные волны
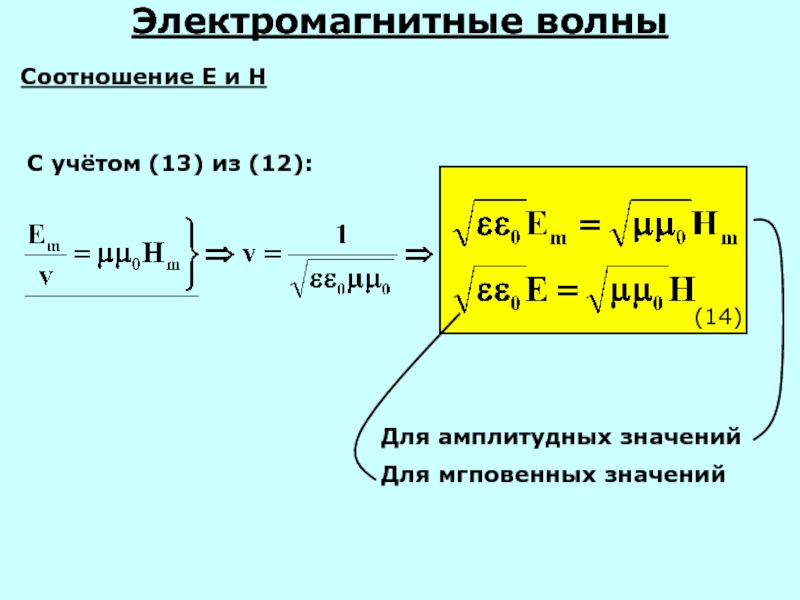
С учётом (13) из (12):
Соотношение Е и Н
(14)
Для амплитудных значений
Для
Слайд 83
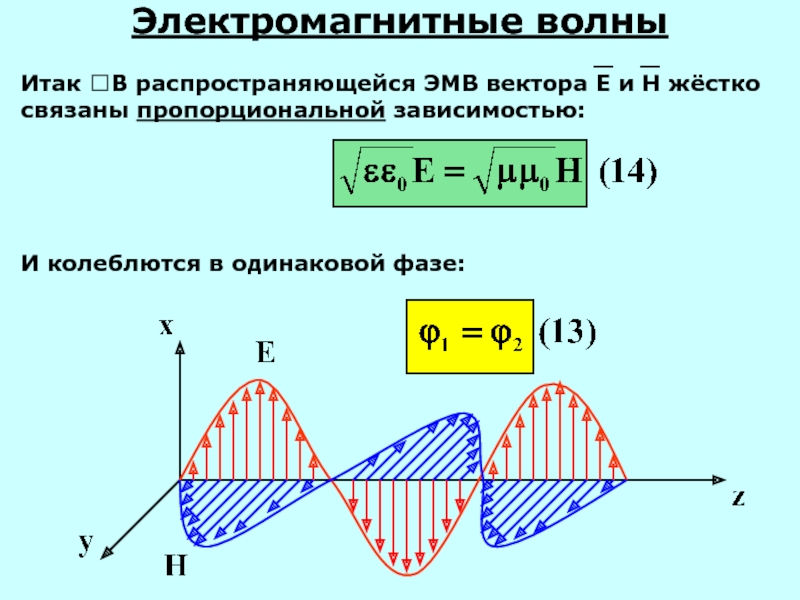
Электромагнитные волны
Итак ?В распространяющейся ЭМВ вектора Е и Н жёстко связаны
И колеблются в одинаковой фазе: