- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физические задачи,приводящие к дифференциальным уравнениям презентация
Содержание
- 1. Физические задачи,приводящие к дифференциальным уравнениям
- 2. Основные определения Дифференциальным называется уравнение,
- 3. Примеры дифференциальных уравнений дифференциальное уравнение 1
- 4. Задачи, приводящие к дифференциальным уравнениям Задача о
- 5. Движение материальной точки под действием силы тяжести
- 6. Решение задачи о движении материальной точки
- 7. Решение задачи о движении материальной точки
- 8. Решение задачи о движении материальной точки F=m
- 9. Решение задачи о движении материальной точки
- 10. Решение дифференциального уравнения (5) (4) (3) (2) (1)
- 11. Нахождение постоянных интегрирования В начальный момент (t=0)
- 12. Материальная точка массой m свободно падает под
- 13. Многовариантная задача Материальная точка находится
- 14. Комментарии для учителя В приложении
- 15. Радиоактивный распад Радиоактивным распадом
- 16. Радиоактивный распад Установлено, что количество
- 17. Радиоактивный распад Время Т,
- 18. Радиоактивный распад Между периодом полураспада
- 19. Радиоактивный распад (основная задача)
- 20. Решение задачи о радиоактивном распаде
- 21. Решение дифференциального уравнения dN=-
- 22. Нахождение константы интегрирования из
- 23. Радиоактивный распад (основная задача) Установить для радиоактивных
- 24. Многовариантная задача Определить какая часть
- 25. Комментарии для учителя
- 26. Задача №1 об истечении жидкости
- 27. Решение задачи №1 об истечении жидкости
- 28. Решение задачи №1 об истечении жидкости
- 29. Решение задачи №1 об истечении жидкости
- 30. Решение задачи №1 об истечении жидкости
- 31. Решение дифференциального уравнения Разделяем переменные:
- 32. В условии говорится, что за
- 33. Теперь мы можем ответить на
- 34. Задача №2 на истечение жидкостей
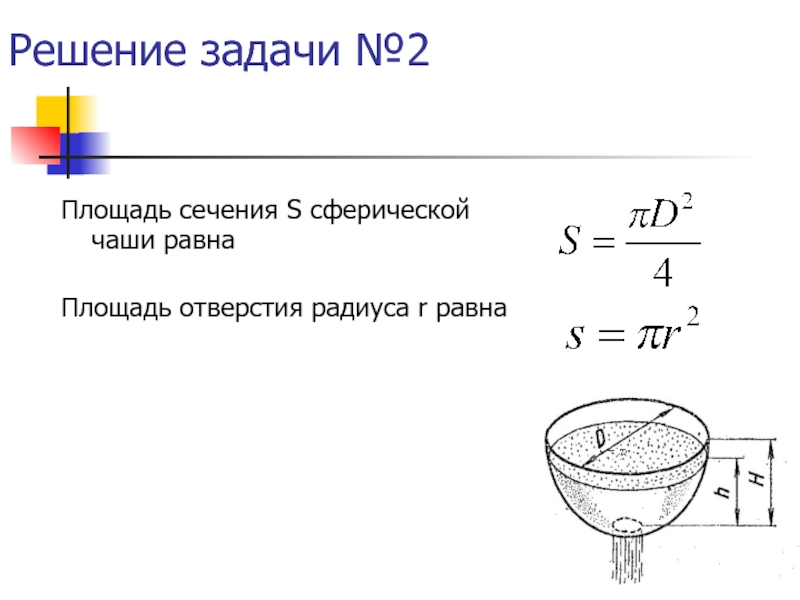
- 35. Решение задачи №2 Площадь сечения S сферической
- 36. Решение задачи №2(начало) - зависимость площади поверхности от высоты столба жидкости в чаше
- 37. Решение задачи №2(продолжение) С другой стороны, этот
- 38. Решение задачи № 2(продолжение)
- 39. Решение задачи № 2(продолжение) Сравним полученные выражения
- 40. Решение дифференциального уравнения Разделяем переменные: Интегрируем:
- 41. Решение задачи №2 (окончание) Теперь мы можем
- 42. Работу выполнили: Ученики 11
Основные определения Дифференциальным называется уравнение, содержащее аргумент, функцию этого аргумента, производные этой функции. Порядком дифференциального уравнения называется наивысший порядок
Слайд 2Основные определения
Дифференциальным называется уравнение, содержащее
аргумент,
функцию этого аргумента,
производные этой функции.
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в данное уравнение
Примеры дифференциальных уравнений
производные этой функции.
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в данное уравнение
Примеры дифференциальных уравнений
Слайд 3Примеры дифференциальных уравнений
дифференциальное уравнение 1 порядка
дифференциальное уравнение 1 порядка
дифференциальное уравнение 2
порядка
Слайд 4Задачи, приводящие к дифференциальным уравнениям
Задача о движении материальной точки под действием
силы тяжести
Задача о радиоактивном распаде
Задачи об истечении жидкости из сосуда
Задача о радиоактивном распаде
Задачи об истечении жидкости из сосуда
Слайд 5Движение материальной точки под действием силы тяжести ( основная задача)
Материальная точка массой m свободно падает под действием силы тяжести. Найти закон движения точки
(без учёта сопротивления воздуха).
Условие.
решение
Многовариантная задача
Слайд 6Решение задачи о движении материальной точки
Возьмём вертикальную ось
с началом отсчёта на поверхности Земли и направим ее вверх.
Положение материальной точки М определяется ее координатой S, которая зависит от времени t.
Пусть в начальный момент времени точка находится на высоте S0.
Положение материальной точки М определяется ее координатой S, которая зависит от времени t.
Пусть в начальный момент времени точка находится на высоте S0.
О
S0
S
M
Слайд 7Решение задачи о движении материальной точки
На точку действует сила,
которая по второму закону Ньютона равна
F=ma (*)
где m - масса точки, a – ускорение
Ускорение является второй производной от функции движения. Формула (*) примет вид:
F=m S//(t)
F=ma (*)
где m - масса точки, a – ускорение
Ускорение является второй производной от функции движения. Формула (*) примет вид:
F=m S//(t)
О
M
Слайд 8Решение задачи о движении материальной точки
F=m S//(t)
По условию задачи
на материальную точку действует только сила тяжести
F=P=-mg,
где g=9,81(м/с2)-ускорение силы тяжести.
Знак «-» показывает, что сила тяжести направлена против направления выбранной оси.
F=P=-mg,
где g=9,81(м/с2)-ускорение силы тяжести.
Знак «-» показывает, что сила тяжести направлена против направления выбранной оси.
О
M
Слайд 9Решение задачи о движении материальной точки
Сравним полученные формулы.
F=m S//(t)
и F=P=-mg
Искомое дифференциальное уравнение имеет вид:
m S//(t) = -mg,
или
S//(t) = -g.
Искомое дифференциальное уравнение имеет вид:
m S//(t) = -mg,
или
S//(t) = -g.
Решение дифференциального уравнения
Слайд 11Нахождение постоянных интегрирования
В начальный момент (t=0)
скорость точки равна vo,
расстояние от начала отсчета
до данной точки равно s0.
расстояние от начала отсчета
до данной точки равно s0.
Слайд 12Материальная точка массой m свободно падает под действием силы тяжести. Найти
закон движения точки
(без учёта сопротивления воздуха).
Ответ.
Многовариантная задача
Слайд 13Многовариантная задача
Материальная точка находится на высоте …… (число в
метрах) над уровнем земли, ее начальная скорость равна ……. (м/с) и направлена …. (вверх, вниз).
Определить
на какой высоте будет находиться материальная точка через … секунд;
через сколько секунд после начала движения точка достигнет наибольшей высоты и какова эта высота;
через сколько секунд после начала движения точка коснется земли?
Определить
на какой высоте будет находиться материальная точка через … секунд;
через сколько секунд после начала движения точка достигнет наибольшей высоты и какова эта высота;
через сколько секунд после начала движения точка коснется земли?
Дополнительные
сведения для учителя
Слайд 14Комментарии для учителя
В приложении 1 к данной работе предложена
расчетная таблица, которая по произвольно выбранным параметрам предлагает ответ.
Таблица выполнена в программе Microsoft Office Excel 2003
Таблица выполнена в программе Microsoft Office Excel 2003
Слайд 15Радиоактивный распад
Радиоактивным распадом называются самопроизвольные превращения ядер атомов
некоторых элементов в ядра других элементов, сопровождающиеся альфа-, бета- и гамма-излучением.
Радиоактивный распад носит статистический характер: ядра атомов распадаются не одновременно все сразу, а в течение всего времени существования данного изотопа.
Радиоактивный распад носит статистический характер: ядра атомов распадаются не одновременно все сразу, а в течение всего времени существования данного изотопа.
Слайд 16Радиоактивный распад
Установлено, что количество атомов, распадающихся в единицу времени,
составляет определённую, постоянную для каждого изотопа часть количества его нераспавшихся атомов.
Эта часть называется постоянной распада
и обозначается буквой λ.
Эта часть называется постоянной распада
и обозначается буквой λ.
Слайд 17Радиоактивный распад
Время Т, в течение которого распадается половина
количества атомов изотопа, называется периодом полураспада этого изотопа.
Периоды полураспада для различных изотопов различны.
Например, для радия Т=1590 лет,
для урана Т=4,6 млрд. лет,
для радиоактивного кобальта Т=5,3 года,
для радона Т=3,82 суток.
Периоды полураспада для различных изотопов различны.
Например, для радия Т=1590 лет,
для урана Т=4,6 млрд. лет,
для радиоактивного кобальта Т=5,3 года,
для радона Т=3,82 суток.
Слайд 19Радиоактивный распад
(основная задача)
Установить для радиоактивных изотопов зависимость количества
нераспавшихся атомов от времени распада
Решение задачи
Условие.
Многовариантная задача
Слайд 20Решение задачи
о радиоактивном распаде
Условие того, что количество атомов N,
распадающихся в единицу времени, составляет определённую, постоянную для каждого изотопа часть количества его нераспавшихся атомов,
выражается формулой
dN=- λNdt,
где λ- постоянная распада
Знак «-» показывает, что число N нераспавшихся атомов с течением времени уменьшается.
выражается формулой
dN=- λNdt,
где λ- постоянная распада
Знак «-» показывает, что число N нераспавшихся атомов с течением времени уменьшается.
Слайд 21Решение дифференциального уравнения
dN=- λNdt
Разделяем переменные:
Интегрируем:
Получаем решение
дифференциального
уравнения:
или
или
Слайд 23Радиоактивный распад
(основная задача)
Установить для радиоактивных изотопов зависимость количества нераспавшихся атомов от
времени распада t и от количества нераспавшихся атомов N0 в начальный момент/
Ответ.
Ответ.
Многовариантная задача
Слайд 24Многовариантная задача
Определить какая часть атомов ….. (указать радиоактивный изотоп)
распадется за ……. (количество) лет
Комментарии для учителя
Слайд 25Комментарии для учителя
В приложении 2 к данной
работе предложена расчетная таблица, которая по произвольно выбранным параметрам предлагает ответ.
Таблица выполнена в программе Microsoft Office Excel 2003
Таблица выполнена в программе Microsoft Office Excel 2003
Слайд 26Задача №1
об истечении жидкости
Резервуар, наполненный водой, имеет форму
цилиндра с высотой Н и площадью основания S.
В дне резервуара сделано отверстие площади s, через которое за 1 час вылилось m/p всей воды.
Через какое временя вся вода вытечет из резервуара?
Решение
В дне резервуара сделано отверстие площади s, через которое за 1 час вылилось m/p всей воды.
Через какое временя вся вода вытечет из резервуара?
Решение
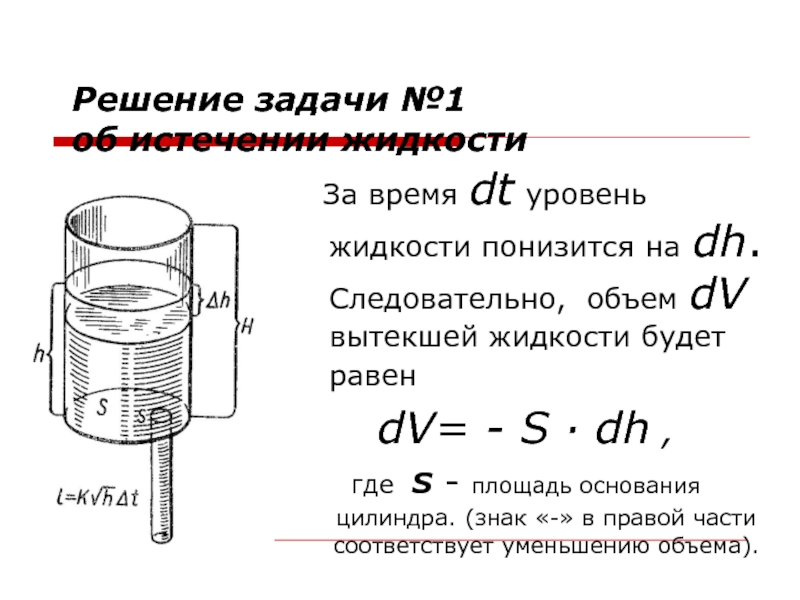
Слайд 27Решение задачи №1
об истечении жидкости
За время dt
уровень жидкости понизится на dh. Следовательно, объем dV вытекшей жидкости будет равен
dV= - S · dh ,
где S - площадь основания цилиндра. (знак «-» в правой части соответствует уменьшению объема).
dV= - S · dh ,
где S - площадь основания цилиндра. (знак «-» в правой части соответствует уменьшению объема).
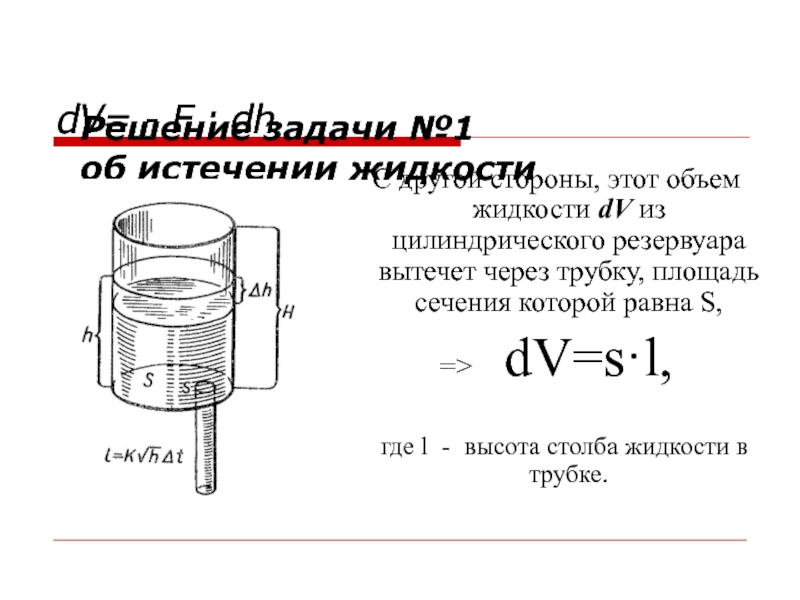
Слайд 28Решение задачи №1
об истечении жидкости
С другой стороны, этот
объем жидкости dV из цилиндрического резервуара вытечет через трубку, площадь сечения которой равна S,
=> dV=s·l,
где l - высота столба жидкости в трубке.
=> dV=s·l,
где l - высота столба жидкости в трубке.
dV= - F · dh
Слайд 29Решение задачи №1
об истечении жидкости
Высота столба жидкости
l в трубке соответствует пути, который капля жидкости прошла со скоростью v за время dt
=> l=v·dt
и
=> l=v·dt
и
dV= - S · dh
dV=s·l
Слайд 30Решение задачи №1
об истечении жидкости
На основе полученных формул
(1)
dV= - S · dh
(2) dV=s·l
(3) l=v·dt
(4)
составим дифференциальное уравнение
(2) dV=s·l
(3) l=v·dt
(4)
составим дифференциальное уравнение
Решение дифференциального уравнения
назад
Слайд 31Решение дифференциального уравнения
Разделяем переменные:
Интегрируем:
Из начальных условий (t=0 и h=H) получаем:
Таким образом
решение принимает вид
Слайд 32 В условии говорится, что за 1 час уровень воды
стал равным m/p от первоначального.
Рассмотрим функцию при условии t=1 и h=m/p∙H, получим:
Данное уравнение примет вид:
или
Рассмотрим функцию при условии t=1 и h=m/p∙H, получим:
Данное уравнение примет вид:
или
Слайд 33 Теперь мы можем ответить на основной вопрос задачи:
через сколько времени вода вытечет из резервуара.
h=0 при
h=0 при
Слайд 34Задача №2 на истечение жидкостей
За какое время вода
вытечет из полусферической чаши диаметром D через круглое отверстие радиусом r, вырезанное на дне чаши?
Решение задачи №2
Решение задачи №2
Слайд 37Решение задачи №2(продолжение)
С другой стороны, этот объем жидкости dV вытекает из
отверстия радиусом r
=>
где l - высота столба жидкости, вытекшей из отверстия.
=>
где l - высота столба жидкости, вытекшей из отверстия.
За время dt уровень жидкости понизится на dh. Следовательно, объем dV вытекшей жидкости будет равен
dV= - S · dh , где
Слайд 38Решение задачи № 2(продолжение)
Высота столба жидкости l в
трубке соответствует пути, который капля жидкости прошла
со скоростью v за время dt
=> l=v·dt
и
Таким образом,
со скоростью v за время dt
=> l=v·dt
и
Таким образом,
Слайд 39Решение задачи № 2(продолжение)
Сравним полученные выражения
и составим дифференциальное уравнение
Решение дифференциального
уравнения
Слайд 40Решение дифференциального уравнения
Разделяем переменные:
Интегрируем:
Из начальных условий (t=0 и h=R) получаем:
Таким образом
решение принимает вид
Слайд 41Решение задачи №2 (окончание)
Теперь мы можем ответить на основной вопрос задачи:
через сколько времени вода вытечет из резервуара.
h=0 при
или
h=0 при
или
Слайд 42Работу выполнили:
Ученики 11 «а» класса
ГОУ СОШ
№420 г.Москвы
Галкин Николай
Киселев Дмитрий
2007 год
Галкин Николай
Киселев Дмитрий
2007 год
