- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Феномен динамического хаоса презентация
Содержание
- 1. Феномен динамического хаоса
- 2. Определения Хаос означает состояние беспорядка и нерегулярности
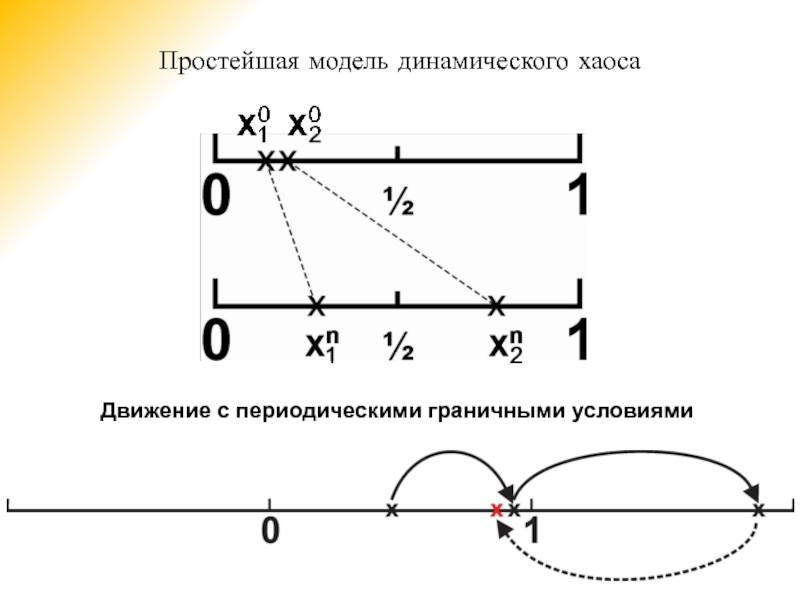
- 3. Простейшая модель динамического хаоса
- 4. Простейшая модель динамического хаоса Движение с периодическими граничными условиями
- 5. Jules Henri Poincaré 1854 – 1912 Edward
- 6. Наука одна – названия разные: теория
- 10. Переход к хаосу путем удвоения периода Неподвижные
- 11. Переход к хаосу путем удвоения периода В
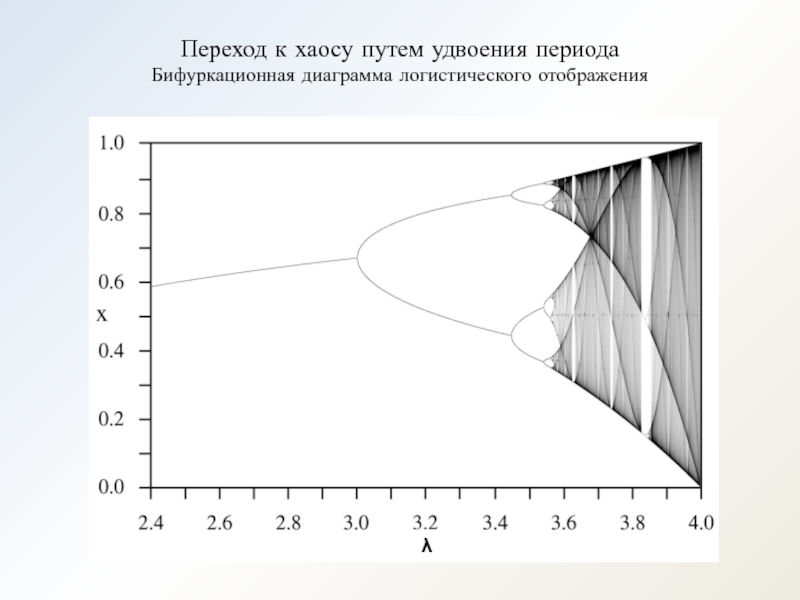
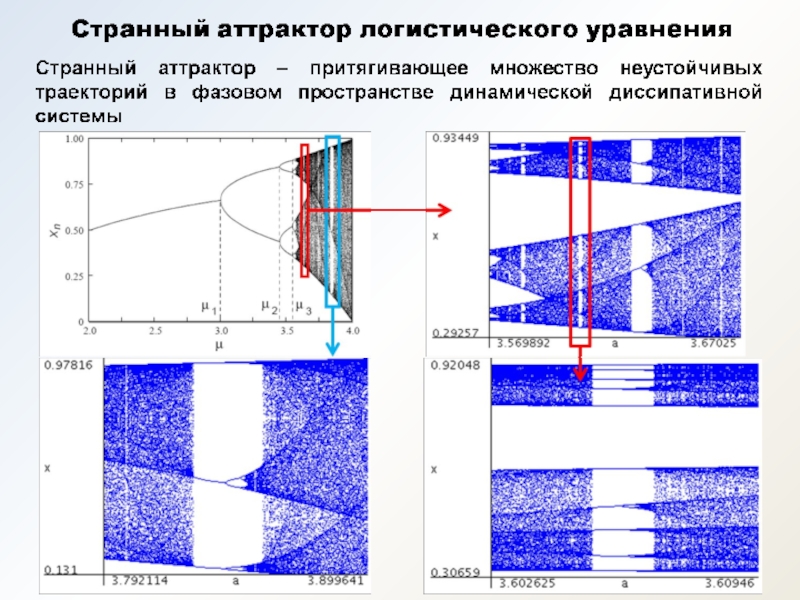
- 12. Переход к хаосу путем удвоения периода Бифуркационная диаграмма логистического отображения
- 14. Развитие нелинейных колебаний конического маятника через последовательность
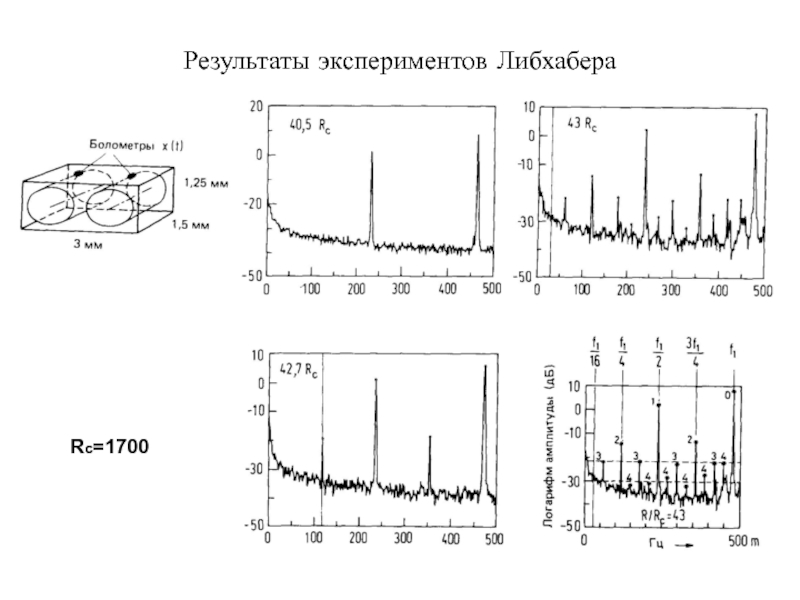
- 16. Результаты экспериментов Либхабера Rc=1700
- 19. Решения уравнений лоренца σ=10, b=8/3 r=0.3 r=16
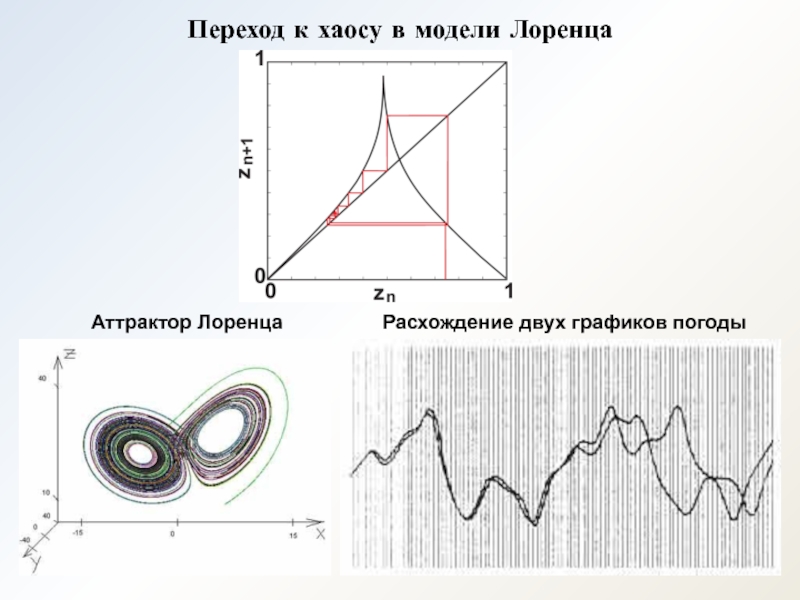
- 20. Переход к хаосу в модели Лоренца Аттрактор Лоренца Расхождение двух графиков погоды
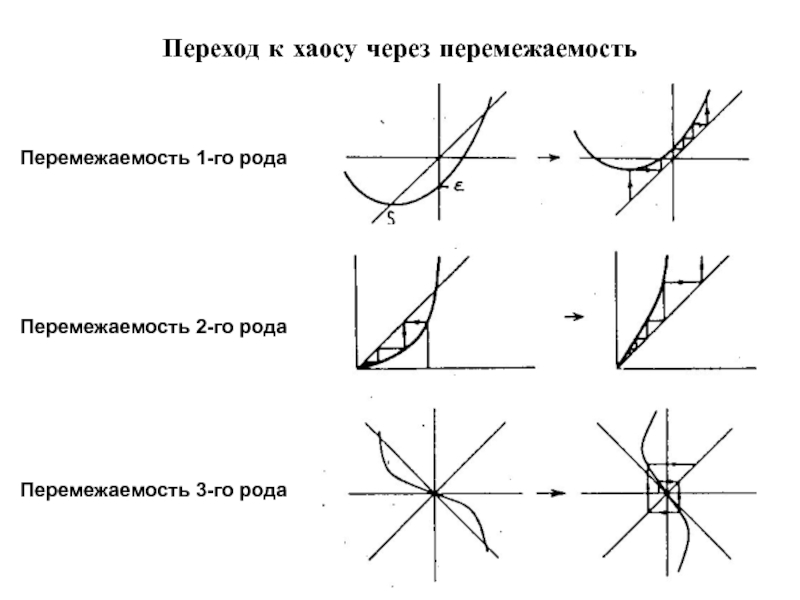
- 21. Переход к хаосу через перемежаемость Перемежаемость 1-го рода Перемежаемость 2-го рода Перемежаемость 3-го рода
- 22. Переход к хаосу через перемежаемость В модели
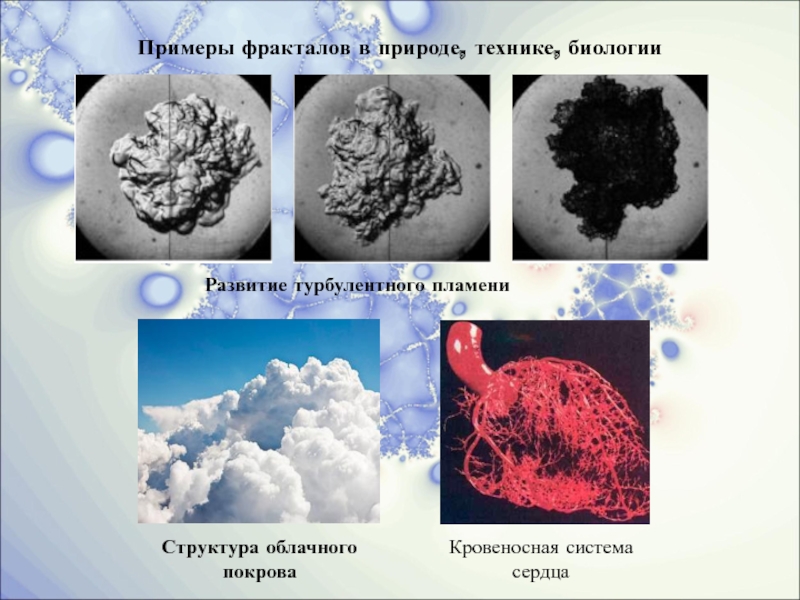
- 24. Примеры фракталов в природе, технике, биологии Развитие турбулентного пламени Структура облачного покрова Кровеносная система сердца
- 26. Странный аттрактор Странный аттрактор имеет фрактальную структуру
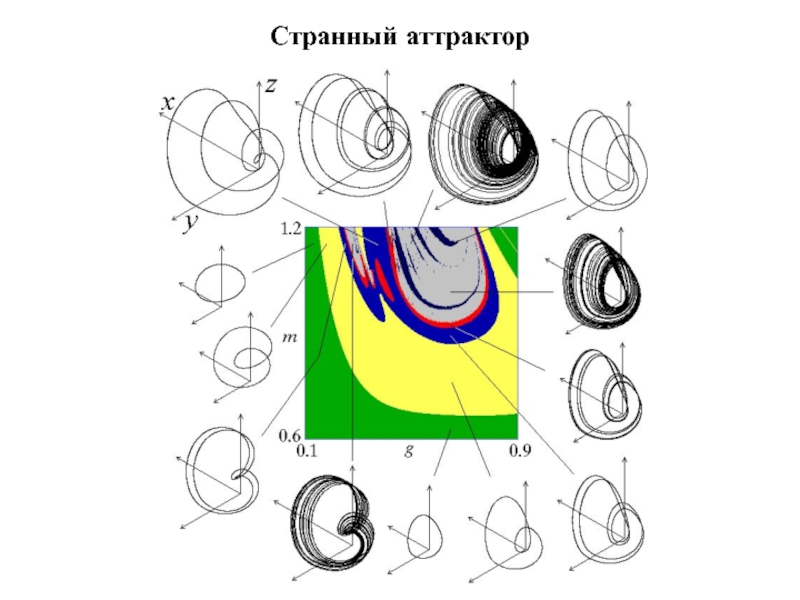
- 27. Странный аттрактор
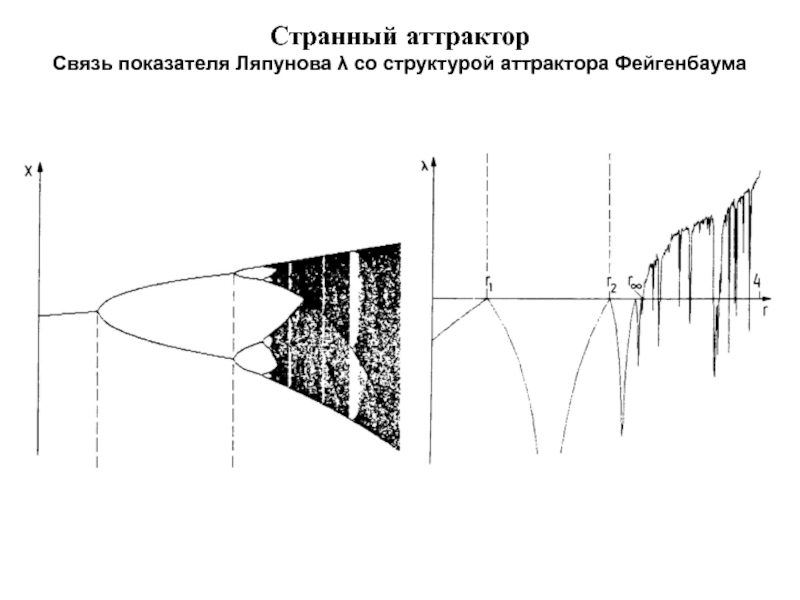
- 28. Странный аттрактор Связь показателя Ляпунова λ со структурой аттрактора Фейгенбаума
- 30. Пример возникновения турбулентности, не описываемый известными моделями
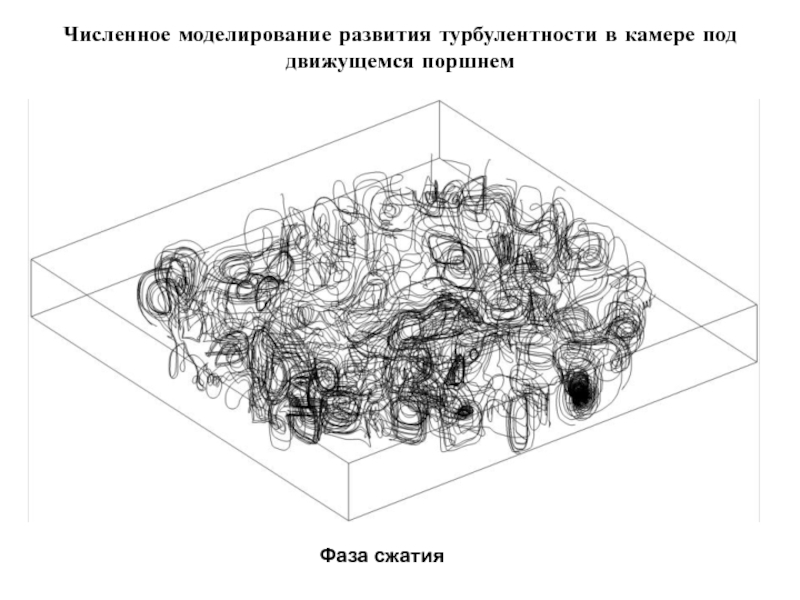
- 31. Численное моделирование развития турбулентности в камере под движущемся поршнем Фаза сжатия
- 32. Численное моделирование развития турбулентности в камере под движущемся поршнем Фаза расширения
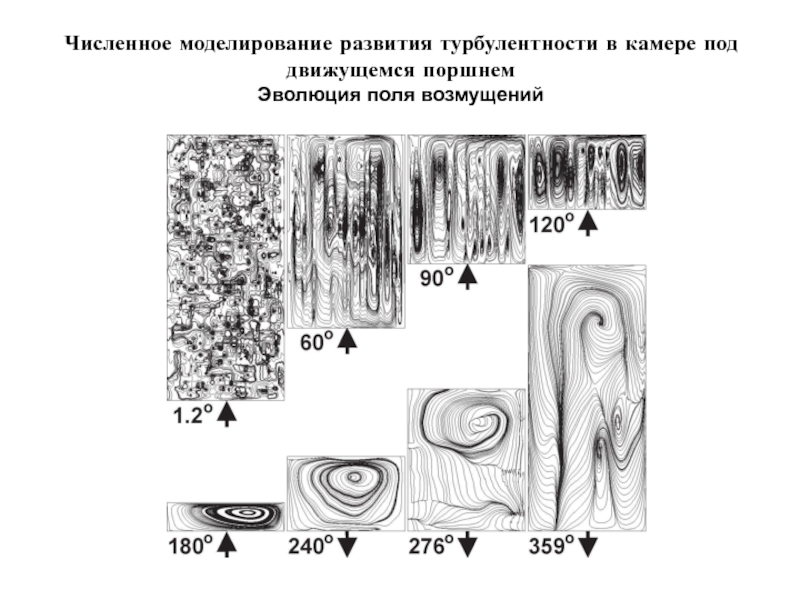
- 33. Численное моделирование развития турбулентности в камере под движущемся поршнем Эволюция поля возмущений
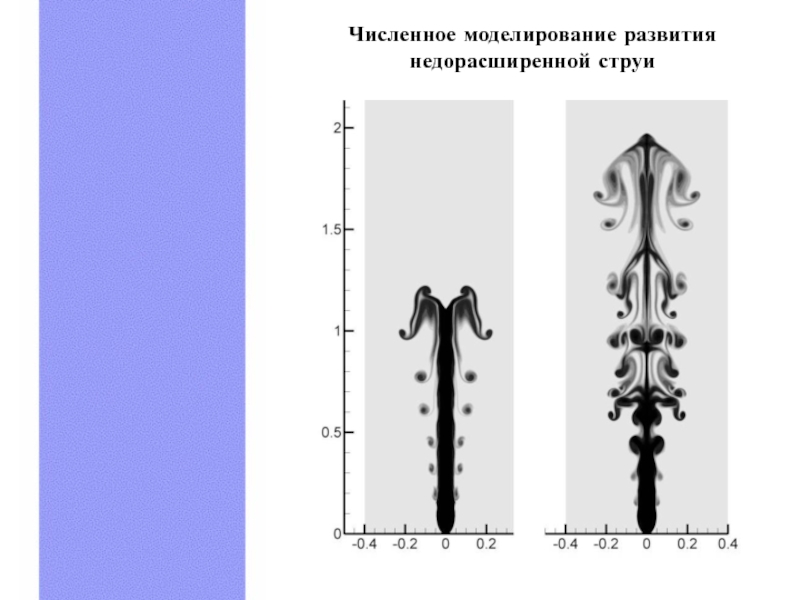
- 34. Численное моделирование развития недорасширенной струи
- 35. Пути перехода к хаосу через каскад бифуркаций
- 36. Примеры самоорганизации и образования структур Рисунок шлифа
- 38. СПАСИБО ЗА ВНИМАНИЕ!
Определения Хаос означает состояние беспорядка и нерегулярности Случайные процессы Хаотические процессы Физическая энциклопедия “Хаос динамический (хаос детерминированный) – нерегулярное апериодическое изменение состояния динамической системы, обладающее основными свойствами случайного процесса”
Слайд 2Определения
Хаос означает состояние беспорядка и нерегулярности
Случайные процессы
Хаотические процессы
Физическая энциклопедия
“Хаос динамический (хаос
детерминированный) – нерегулярное апериодическое изменение состояния динамической системы, обладающее основными свойствами случайного процесса”
Слайд 5Jules Henri Poincaré
1854 – 1912
Edward Norton Lorenz
1917 – 2008
Benoît B.
Mandelbrot
1924 – 2010
1924 – 2010
Mitchell Jay Feigenbaum
1944
Hermann Haken
1928
Илья Пригожин
1917 - 2003
Авторы теории динамического хаоса
Слайд 6Наука одна – названия разные:
теория диссипативных структур (И. Пригожин)
теория
динамического хаоса (М. Фейгенбаум)
синергетика (Г. Хакен)
нелинейная динамика (С.П. Курдюмов)
синергетика (Г. Хакен)
нелинейная динамика (С.П. Курдюмов)
Сергей Павлович
Курдюмов
1928 – 2004
Создатель советской и российской школы синергетики
Александр Александрович
Андронов
1901 – 1952
Советский физик, академик, создатель совместно с Л.И. Мандельштамом научной школы нелинейной динамики
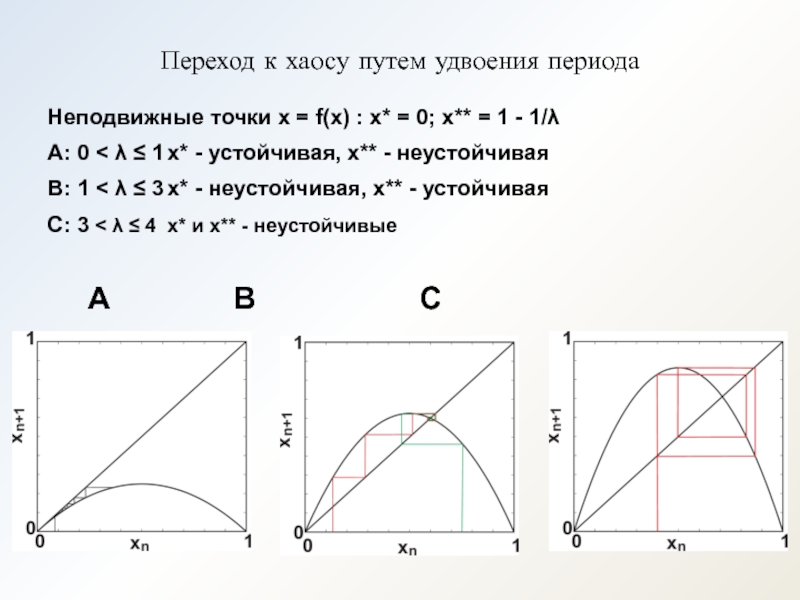
Слайд 10Переход к хаосу путем удвоения периода
Неподвижные точки x = f(x) :
x* = 0; x** = 1 - 1/λ
A: 0 < λ ≤ 1 x* - устойчивая, х** - неустойчивая
B: 1 < λ ≤ 3 х* - неустойчивая, х** - устойчивая
C: 3 < λ ≤ 4 х* и х** - неустойчивые
А В С
A: 0 < λ ≤ 1 x* - устойчивая, х** - неустойчивая
B: 1 < λ ≤ 3 х* - неустойчивая, х** - устойчивая
C: 3 < λ ≤ 4 х* и х** - неустойчивые
А В С
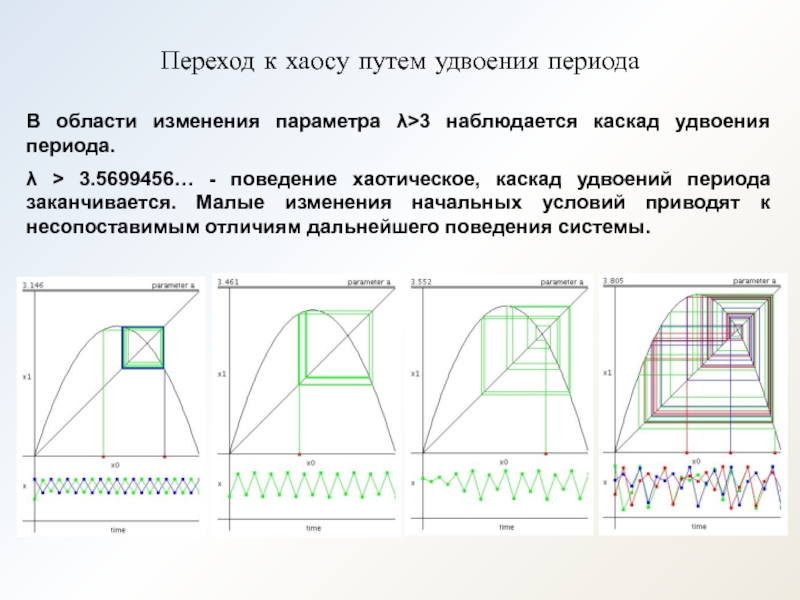
Слайд 11Переход к хаосу путем удвоения периода
В области изменения параметра λ>3 наблюдается
каскад удвоения периода.
λ > 3.5699456… - поведение хаотическое, каскад удвоений периода заканчивается. Малые изменения начальных условий приводят к несопоставимым отличиям дальнейшего поведения системы.
λ > 3.5699456… - поведение хаотическое, каскад удвоений периода заканчивается. Малые изменения начальных условий приводят к несопоставимым отличиям дальнейшего поведения системы.
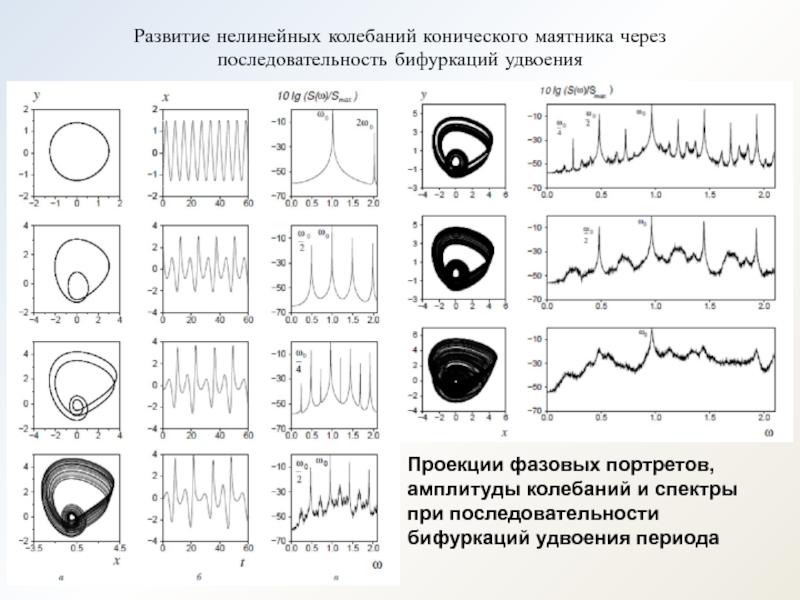
Слайд 14Развитие нелинейных колебаний конического маятника через последовательность бифуркаций удвоения
Проекции фазовых портретов,
амплитуды колебаний и спектры при последовательности бифуркаций удвоения периода
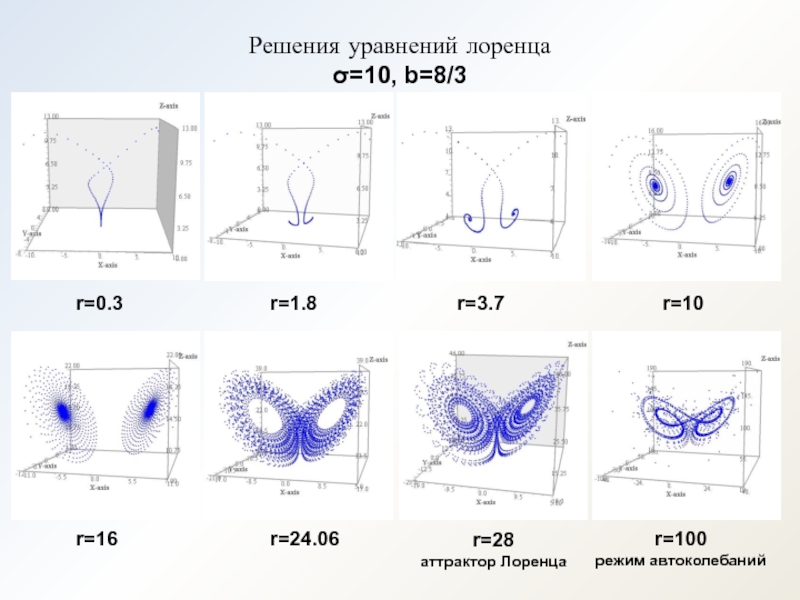
Слайд 19Решения уравнений лоренца
σ=10, b=8/3
r=0.3
r=16
r=1.8
r=24.06
r=3.7
r=28
аттрактор Лоренца
r=10
r=100
режим автоколебаний
Слайд 21Переход к хаосу через перемежаемость
Перемежаемость 1-го рода
Перемежаемость 2-го рода
Перемежаемость 3-го рода
Слайд 22Переход к хаосу через перемежаемость
В модели Лоренца число осцилляций до установления
стационарного режима (время распада) ведет себя как:
Слайд 24Примеры фракталов в природе, технике, биологии
Развитие турбулентного пламени
Структура облачного
покрова
Кровеносная система
сердца
Слайд 26Странный аттрактор
Странный аттрактор имеет фрактальную структуру и размерность.
Аттрактор Фейгенбаума: D=0.543
Аттрактор Лоренца:
D=2.06
Свойства странного аттрактора:
занимает ограниченную область в фазовом пространстве, к которой притягиваются все траектории из области притяжения;
несмотря на сжатие в объеме, не происходит сокращения длин во всех направлениях;
разводит сколь угодно близкие траектории на конечное расстояние (отличие уже в первом знаке);
сохраняет статистические свойства случайных последовательностей;
порождает эргодичность;
порождает стохастичность в поведении показателя Ляпунова
Свойства странного аттрактора:
занимает ограниченную область в фазовом пространстве, к которой притягиваются все траектории из области притяжения;
несмотря на сжатие в объеме, не происходит сокращения длин во всех направлениях;
разводит сколь угодно близкие траектории на конечное расстояние (отличие уже в первом знаке);
сохраняет статистические свойства случайных последовательностей;
порождает эргодичность;
порождает стохастичность в поведении показателя Ляпунова
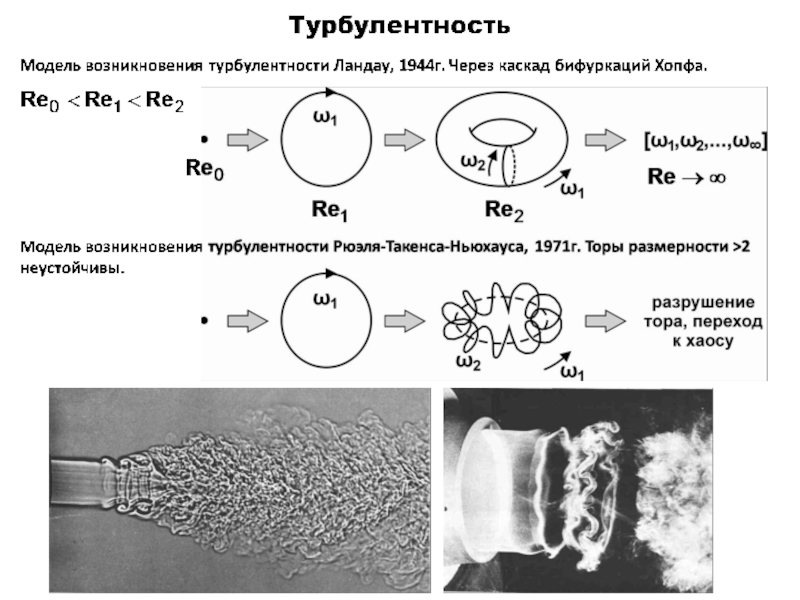
Слайд 30Пример возникновения турбулентности, не описываемый известными моделями перехода к хаосу
Гидродинамическое течение
при различных значениях числа Рейнольдса Re. При малых Re течение ламинарное (а); с ростом Re течение сначала становится волнообразным (периодическим) (в) и, наконец, турбулентным (д). На рисунке для каждого значения числа Рейнольдса изображено изменение со временем одной компоненты скорости, измеренной в некоторой фиксированной точке потока. Показана также спектральная функция P(ω), соответствующая представленной зависимости скорости от времени.
Слайд 32Численное моделирование развития турбулентности в камере под движущемся поршнем
Фаза расширения
Слайд 33Численное моделирование развития турбулентности в камере под движущемся поршнем
Эволюция поля возмущений
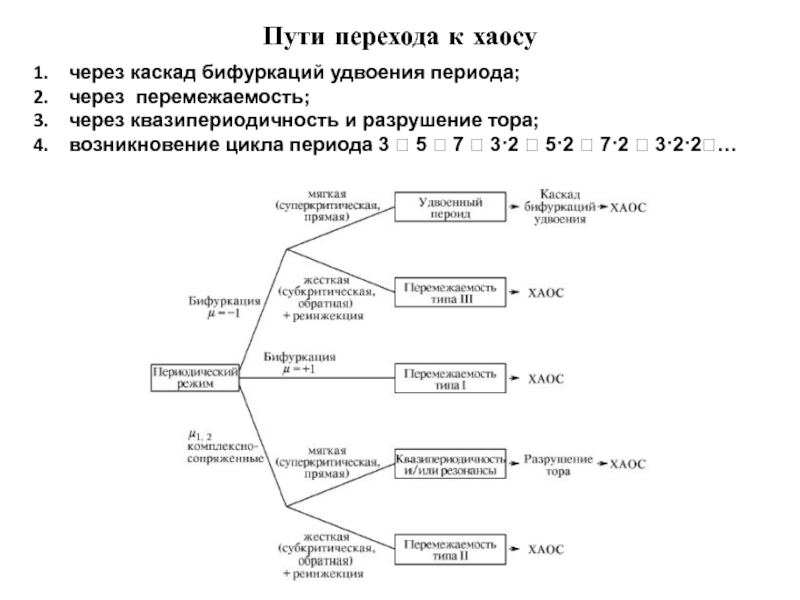
Слайд 35Пути перехода к хаосу
через каскад бифуркаций удвоения периода;
через перемежаемость;
через квазипериодичность и
разрушение тора;
возникновение цикла периода 3 ? 5 ? 7 ? 3·2 ? 5·2 ? 7·2 ? 3·2·2?…
возникновение цикла периода 3 ? 5 ? 7 ? 3·2 ? 5·2 ? 7·2 ? 3·2·2?…
Слайд 36Примеры самоорганизации
и образования структур
Рисунок шлифа дальневосточного скарна
Ячейки Бенара
Последовательность структурирования популяции амеб
Dictyostelium
