- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Естественный способ задания движения презентация
Содержание
Слайд 2▼
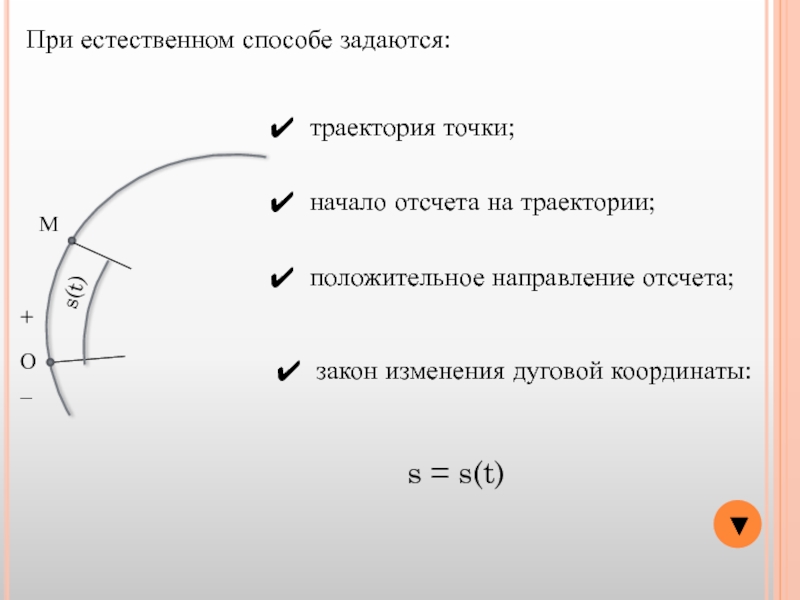
При естественном способе задаются:
траектория точки;
начало отсчета на траектории;
положительное
закон изменения дуговой координаты:
s = s(t)
О
−
+
М
s(t)
Слайд 3▼
О
−
+
М
s
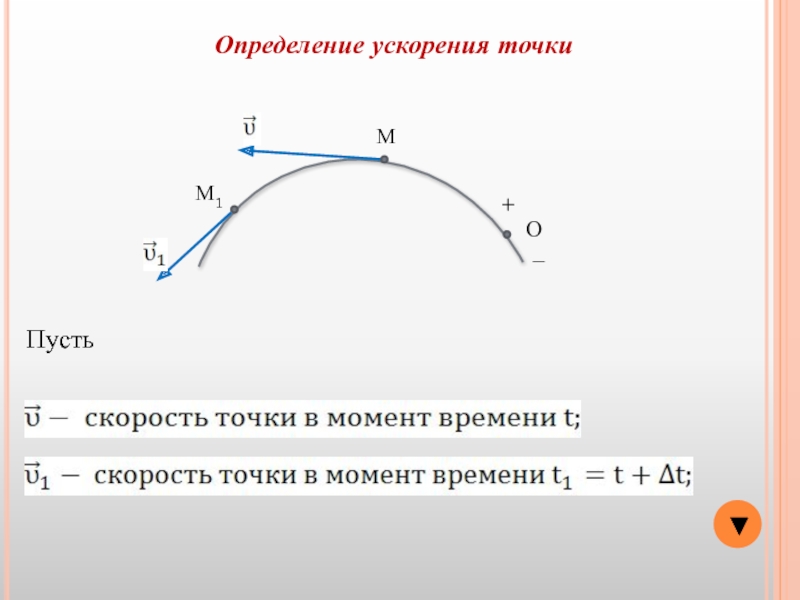
Определение скорости точки
М1
s1
Δs
Пусть за время t точка прошла путь ОМ =
За время t1 = t + Δt точка прошла путь ОМ1 = s1.
Δ s – путь, пройденный точкой за время Δt.
Слайд 4Отношении пройденного пути Δs к промежутку времени Δt называется средней скоростью
Скорость точки в данный момент времени находится как предел средней скорости при стремлении промежутка времени к нулю, то есть
▼
Слайд 5
М
▼
Следовательно,
Алгебраическое значение скорости в данный момент времени равно производной от дуговой
Вектор скорости направлен по касательной к траектории точки в сторону движения.
Слайд 7▼
О
−
+
М
М1
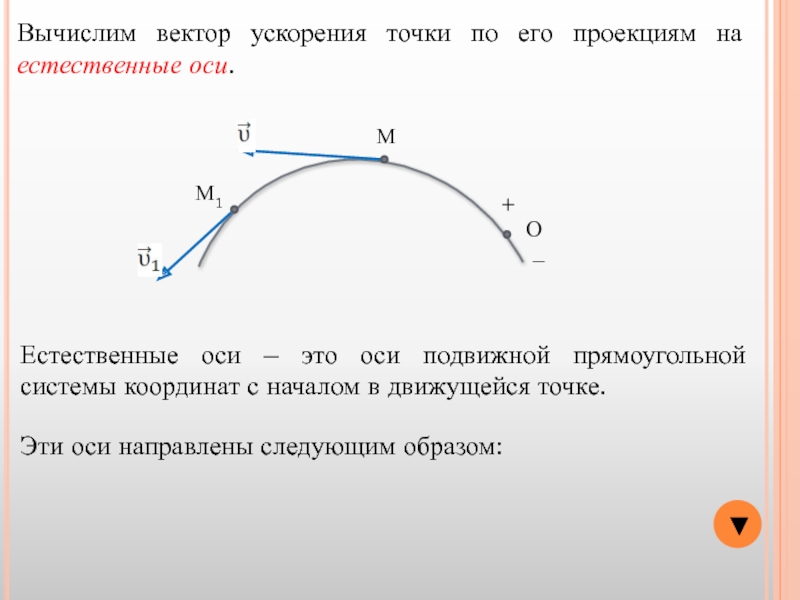
Вычислим вектор ускорения точки по его проекциям на естественные оси.
Естественные
Эти оси направлены следующим образом:
Слайд 8▼
О
−
+
М
М1
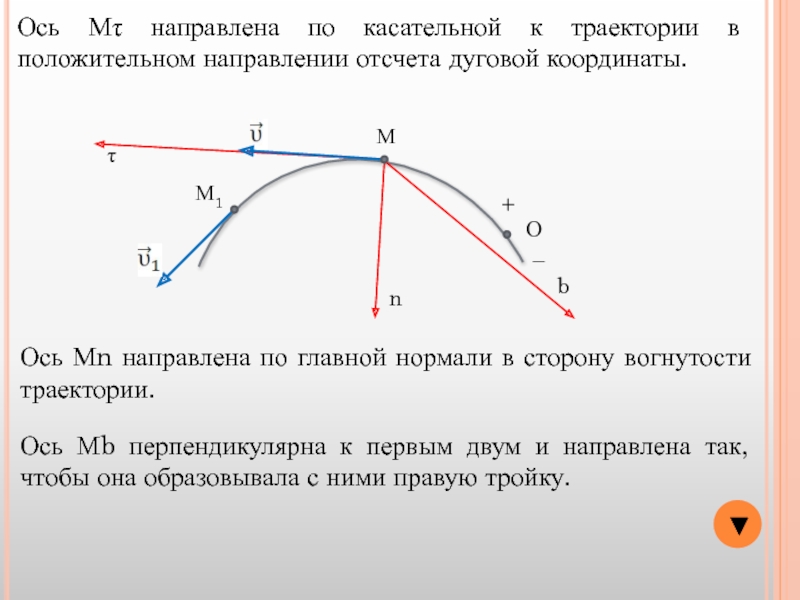
Ось Мτ направлена по касательной к траектории в положительном направлении отсчета
τ
Ось Мn направлена по главной нормали в сторону вогнутости траектории.
n
Ось Мb перпендикулярна к первым двум и направлена так, чтобы она образовывала с ними правую тройку.
b
Слайд 9▼
О
−
+
М
М1
Так как ускорение лежит в соприкасающейся плоскости, то проекция вектора ускорения
τ
n
b
Таким образом
Слайд 10▼
О
−
+
М
τ
n
b
где
Проекция ускорения точки на касательную равна первой производной от численной величины
Эта составляющая характеризует изменение скорости по модулю.
Слайд 11▼
О
−
+
М
τ
n
b
Проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус
Эта составляющая характеризует изменение скорости по направлению.
Слайд 12▼
О
−
+
М
τ
n
b
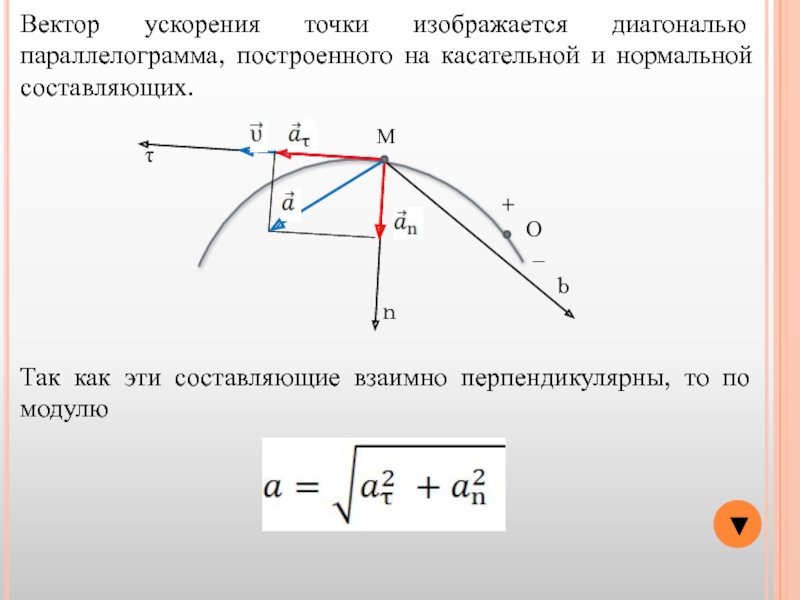
Вектор ускорения точки изображается диагональю параллелограмма, построенного на касательной и нормальной
Так как эти составляющие взаимно перпендикулярны, то по модулю