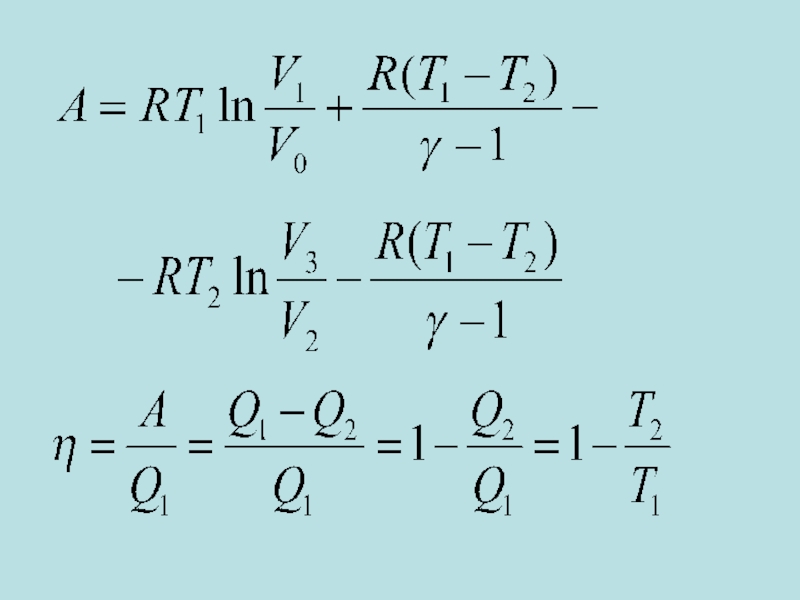- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Энтропия. Изменение энтропии в изопроцессах презентация
Содержание
- 2. Энтропия Адиабатические процессы в термодинамических системах могут
- 5. Следовательно, S = const, адиабатный процесс по
- 6. Изопроцессы могут быть изображены графически в координатных
- 7. Удобство координатной системы р, V В
- 8. Круговые (замкнутые) процессы Совокупность термодинамических процессов, в
- 9. Тепловая машина Циклически действующее устройство, превращающее
- 12. Для того чтобы поршень совершил полезную работу, необходимо выполнить условие: А2
- 13. Сложим два уравнения и
- 14. Процесс возвращения
- 15. Цикл Карно Никола Леонард Сади Карно –французский
- 16. из всех периодически действующих тепловых машин, имеющих
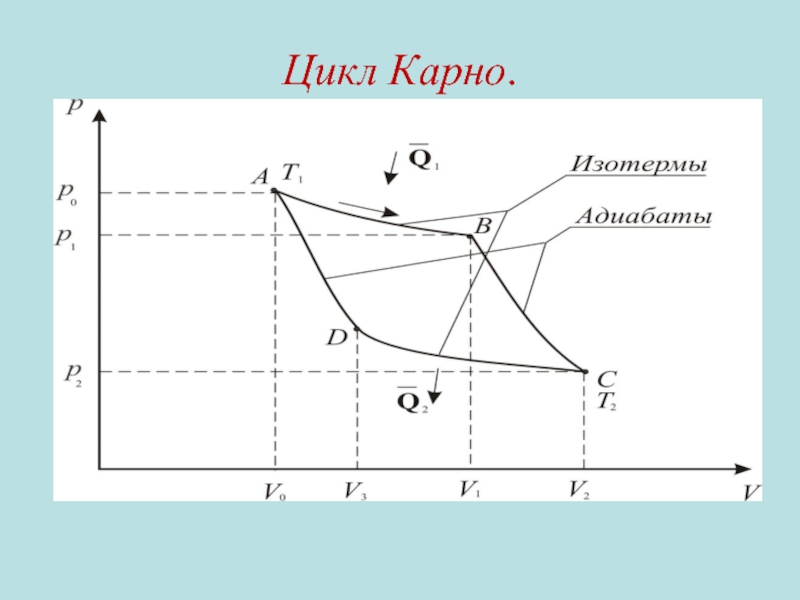
- 17. Цикл Карно.
- 18. Процесс А-В – изотермическое расширение Процесс
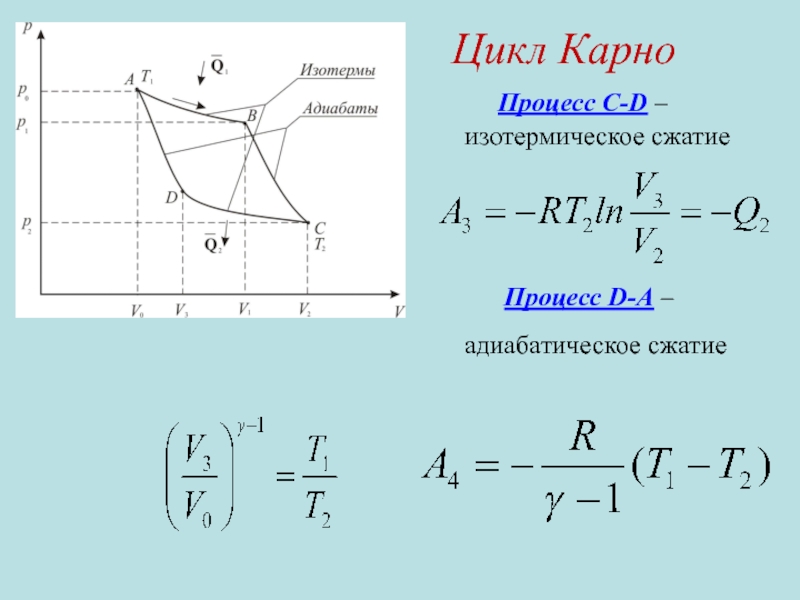
- 19. Процесс С-D – изотермическое сжатие Процесс D-A – адиабатическое сжатие Цикл Карно
- 21. КПД цикла Карно η < 1 и
- 22. Цикл Карно в координатах S-T Изотермы:
- 23. Теоремы Карно. К.п.д. η обратимой идеальной тепловой
- 24. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 25. Функция состояния, дифференциал которой
- 26. При любом необратимом процессе в замкнутой системе
- 27. Так как для каждого из подвергнутых исследованию
- 28. 1. круговые процессы, в течение которых система
- 29. 2. круговые процессы, в течение которых система
- 30. осуществить такой круговой процесс, в результате которого
- 31. Пусть получение теплоты извне и отдача ее
- 32. В результате круговых процессов, идущих в обратном
- 33. Второе начало термодинамики 1) невозможны круговые процессы,
- 34. Совершение над газом работы на элементарном участке
- 35. U2-U1=Q - A Применяя это соотношение к
- 36. Первый и второй законы термодинамики
- 37. Q =Q Второй закон термодинамики ограничивает
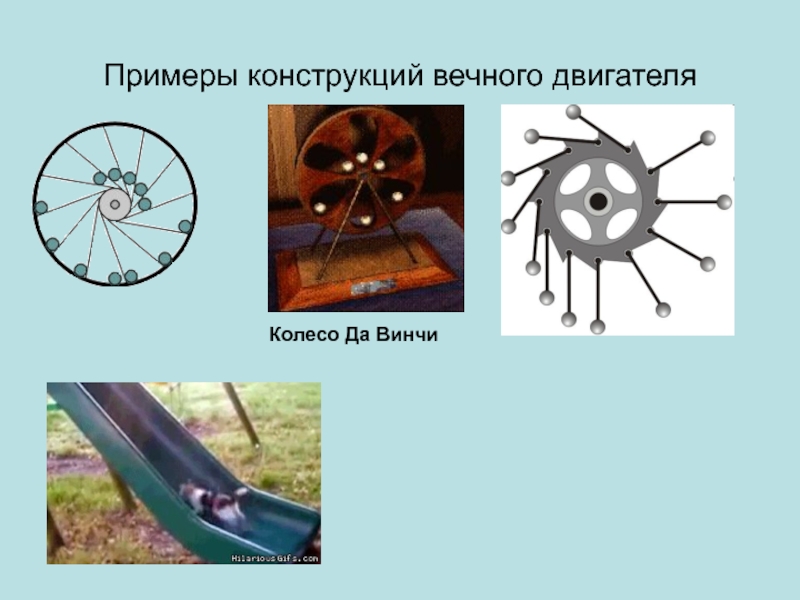
- 38. Примеры конструкций вечного двигателя Колесо Да Винчи
- 39. Q1 =Q1-Q2 Q2 нагреватель холодильник
- 40. Можно показать, что при заданных температурах источника
- 41. Идеальный газ
- 42. Идеальным газом называется газ, который удовлетворяет
- 43. Выведем «основное уравнение кинетической теории газов», связывающее
- 44. Согласно второму закону Ньютона, это изменение должно
- 45. Мы предполагали, что скорости молекул одинаковы; если
- 46. Функцию f(v) = ΔNI(N ·Δv), показывающую относительное
- 48. Уравнение состояния идеального газа Пусть в объеме
- 49. при данном р и Т V
- 50. Сравним уравнение с основным уравнением кинетической теории
Слайд 2Энтропия
Адиабатические процессы в термодинамических системах могут быть равновесными и неравновесными. Для
Энтропия есть такая функция состояния системы, элементарное изменение которой при равновесном переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс
для бесконечно малого изменения состояния системы
Слайд 5Следовательно, S = const, адиабатный процесс по другому называют – изоэнтропийным
Энтропия системы пропорциональна массе (или числу частиц) этой системы Q=c m ΔT
Масса системы представляется в виде суммы масс ее составных частей, поэтому энтропия всей системы будет равна сумме энтропии ее составных частей, т. е. энтропия есть аддитивная величина.
Во всех случаях, когда система получает извне теплоту, то Q — положительно, следовательно, S2 > S1 и энтропия системы увеличивается.
Если же система отдаст теплоту, то Q имеет отрицательный знак и, следовательно, S2 < S1; энтропия системы уменьшается.
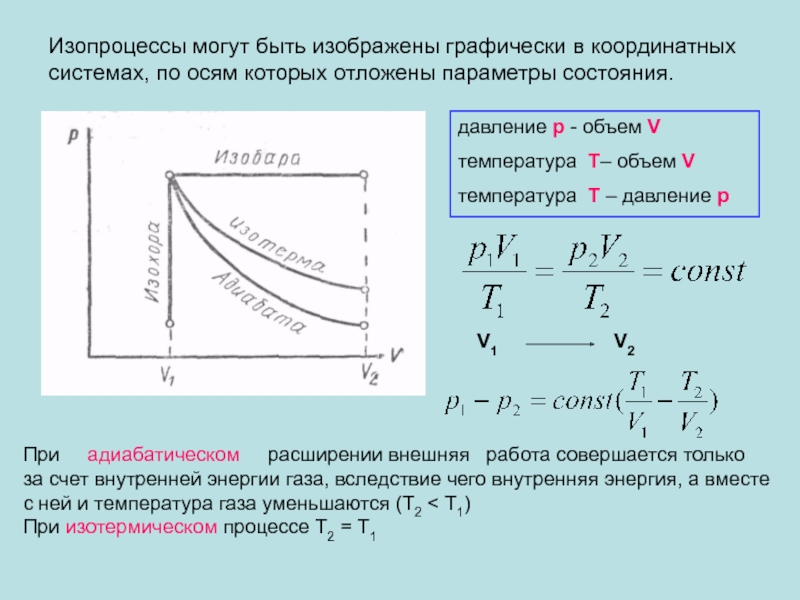
Слайд 6Изопроцессы могут быть изображены графически в координатных системах, по осям которых
давление p - объем V
температура Т– объем V
температура Т – давление p
V1 V2
При адиабатическом расширении внешняя работа совершается только
за счет внутренней энергии газа, вследствие чего внутренняя энергия, а вместе с ней и температура газа уменьшаются (Т2 < T1)
При изотермическом процессе Т2 = T1
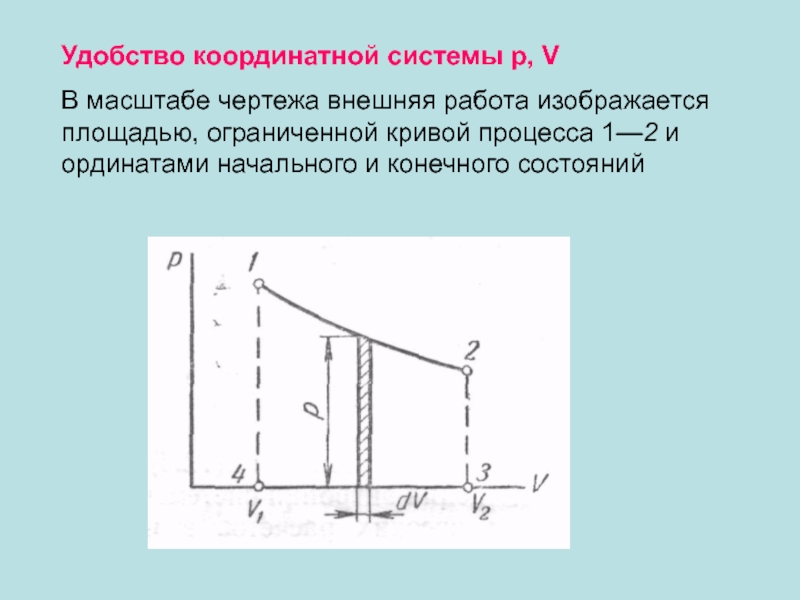
Слайд 7Удобство координатной системы р, V
В масштабе чертежа внешняя работа изображается
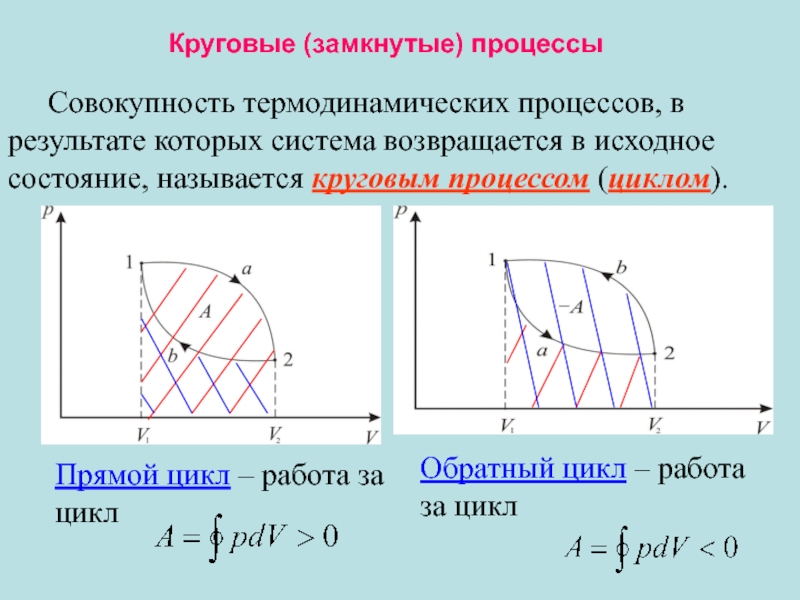
Слайд 8Круговые (замкнутые) процессы
Совокупность термодинамических процессов, в результате которых система возвращается в
Прямой цикл – работа за цикл
Обратный цикл – работа за цикл
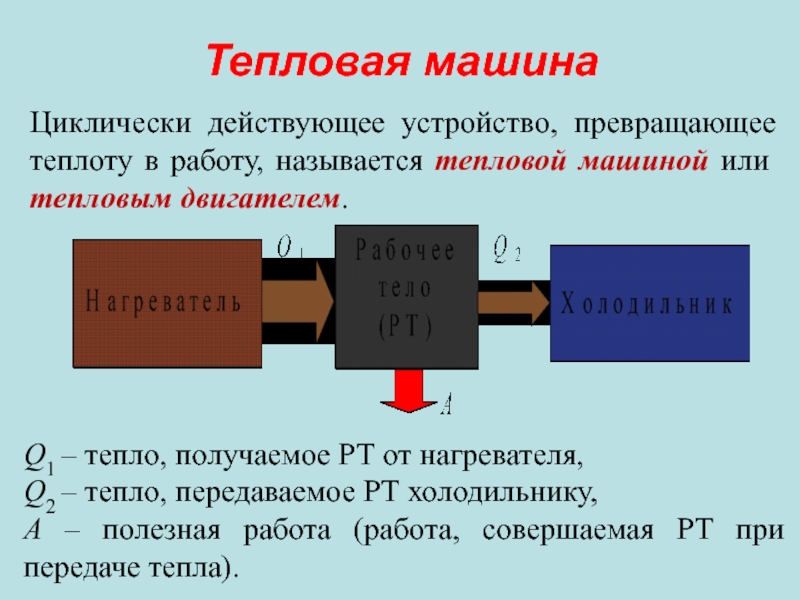
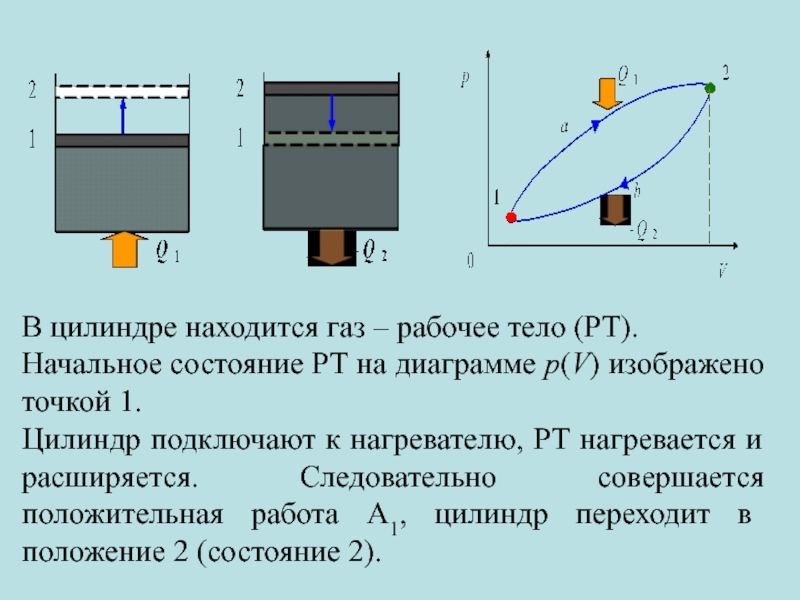
Слайд 9Тепловая машина
Циклически действующее устройство, превращающее теплоту в работу, называется тепловой машиной
Q1 – тепло, получаемое РТ от нагревателя,
Q2 – тепло, передаваемое РТ холодильнику,
А – полезная работа (работа, совершаемая РТ при передаче тепла).
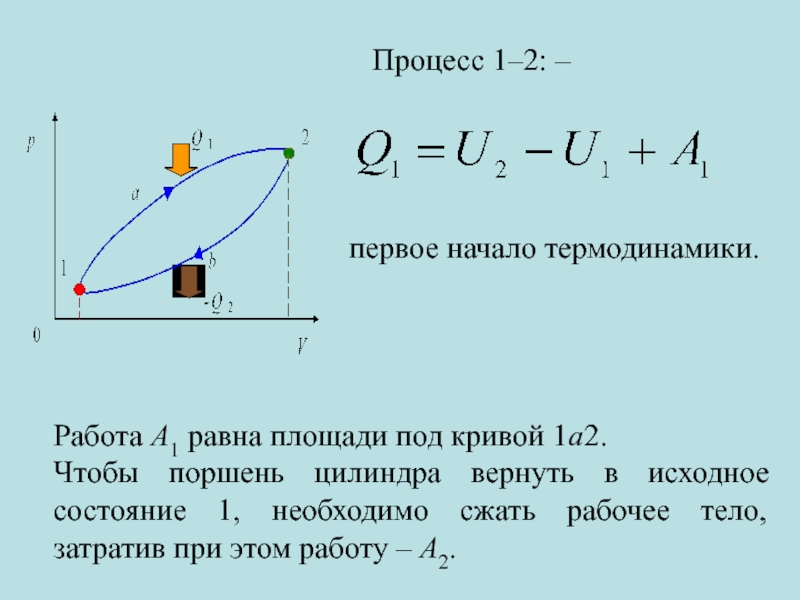
Слайд 12
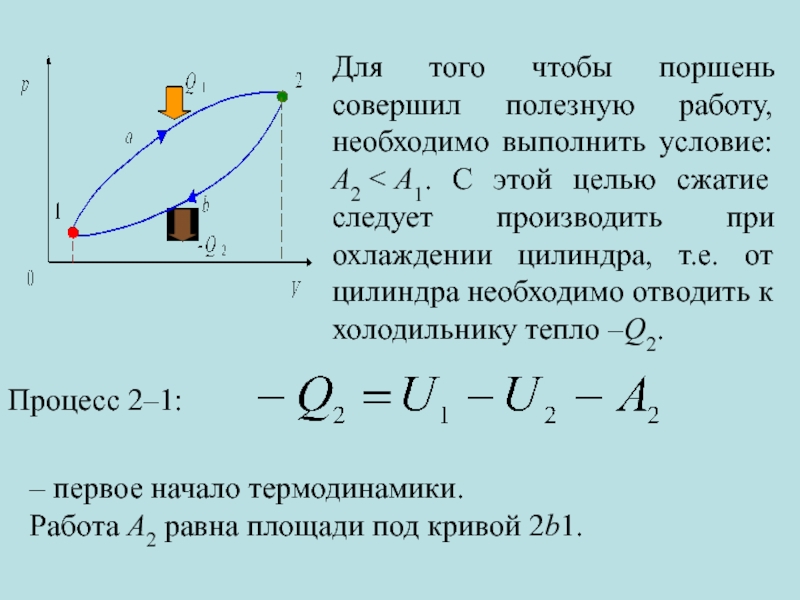
Для того чтобы поршень совершил полезную работу, необходимо выполнить условие: А2
Процесс 2–1:
– первое начало термодинамики.
Работа А2 равна площади под кривой 2b1.
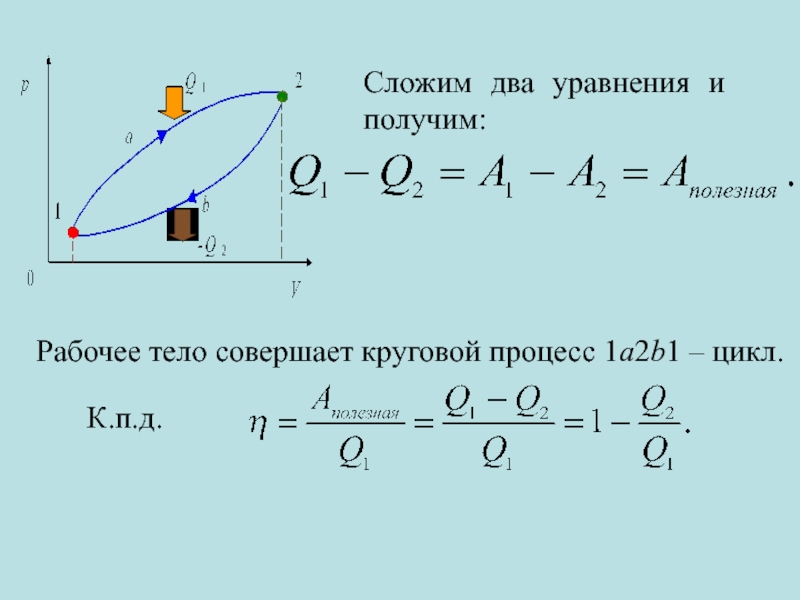
Слайд 14
Процесс возвращения рабочего тела в исходное состояние происходит при более низкой
Слайд 15Цикл Карно
Никола Леонард Сади Карно –французский офицер инженерных войск, в 1824
Ввел понятие кругового и обратимого процессов, идеального цикла тепловых машин, заложил тем самым основы их теории. Пришел к понятию механического эквивалента теплоты.
Слайд 16 из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей и
Карно вывел теорему, носящую теперь его имя:
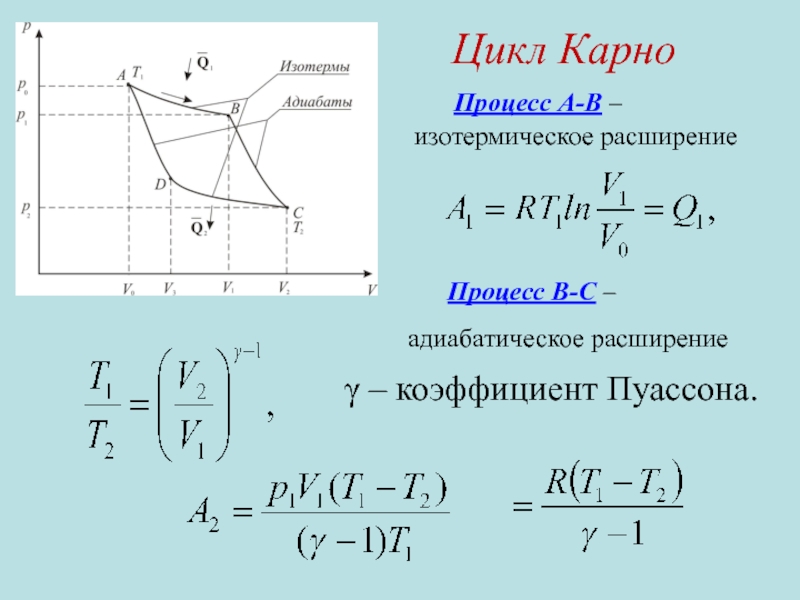
Слайд 18 Процесс А-В –
изотермическое расширение
Процесс В-С –
адиабатическое расширение
γ – коэффициент
Цикл Карно
Слайд 21 КПД цикла Карно η < 1 и зависит от разности температур
Если Т2 = 0, то η = 1, что невозможно, т.к. абсолютный нуль температуры не существует.
Если Т1 = ∞, то η = 1, что невозможно, т.к. бесконечная температура не достижима.
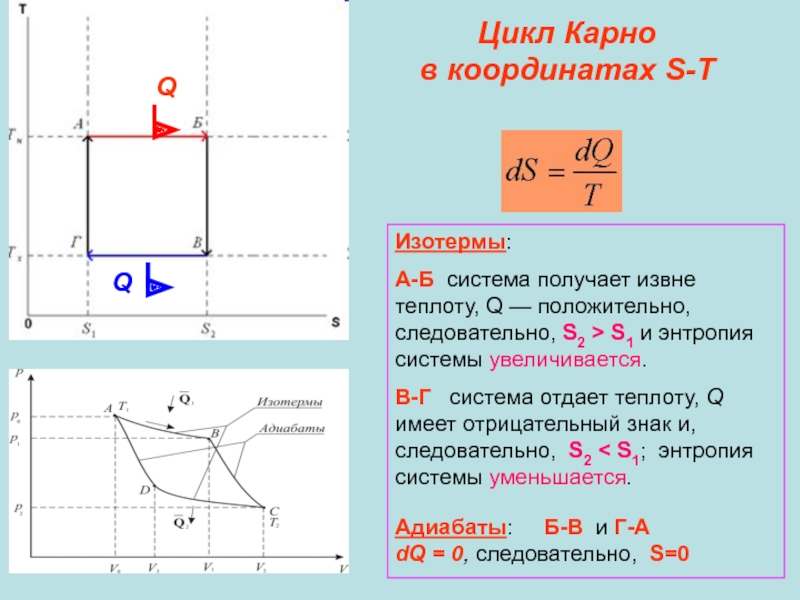
Слайд 22Цикл Карно
в координатах S-T
Изотермы:
А-Б система получает извне теплоту, Q —
В-Г система отдает теплоту, Q имеет отрицательный знак и, следовательно, S2 < S1; энтропия системы уменьшается.
Адиабаты: Б-В и Г-А
dQ = 0, следовательно, S=0
Q
Q
Слайд 23Теоремы Карно.
К.п.д. η обратимой идеальной тепловой машины Карно не зависит от
2. К.п.д. необратимой машины Карно не может быть больше к.п.д. обратимой машины Карно.
Слайд 25Функция состояния, дифференциал которой ,
Энтропия обозначается S – это отношение полученной или отданной теплоты к температуре при которой произошла эта отдача.
Изучение всевозможных равновесных круговых процессов показало, что сумма отношений ΔQl/T1, подсчитанных для участков процесса, при которых система получает теплоту, всегда равна сумме отношений ΔQ2/T2, вычисленных для участков процесса, при которых система отдает теплоту
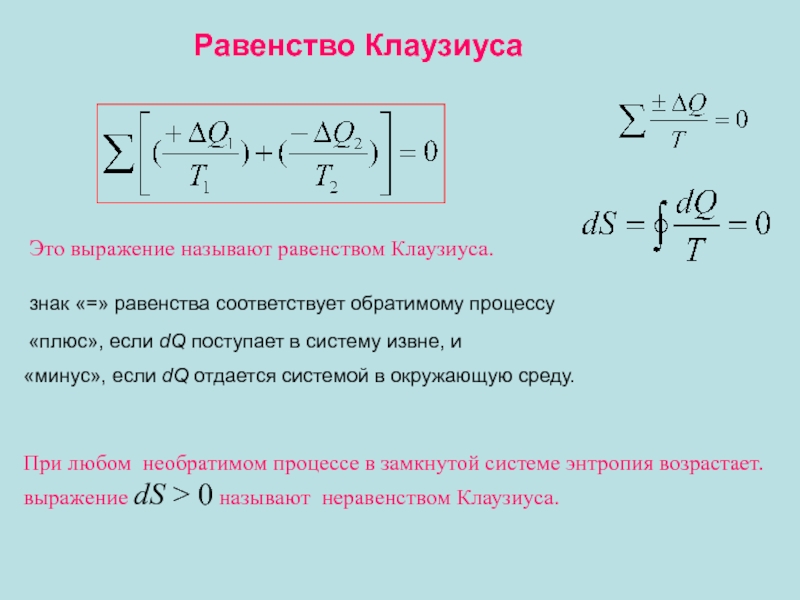
Слайд 26При любом необратимом процессе в замкнутой системе энтропия возрастает.
выражение dS
Это выражение называют равенством Клаузиуса.
знак «=» равенства соответствует обратимому процессу
«плюс», если dQ поступает в систему извне, и
«минус», если dQ отдается системой в окружающую среду.
Равенство Клаузиуса
Слайд 27Так как для каждого из подвергнутых исследованию круговых процессов сумма
Для того чтобы найти формулировку единого закона, произведем исследование равенства Клаузиуса и вытекающих из него следствий.
Следствия из равенства Клаузиуса :
Слайд 281. круговые процессы, в течение которых система только получает, но не
В этом случае все элементарные количества теплоты были бы со знаком «плюс», сумма была бы отлична от нуля. Т.е. отсутствовали бы
отрицательные члены этой суммы , соответствующие отдаче тепла от системы в окружающую среду.
такие процессы не противоречили бы первому закону термодинамики, т. е. закону сохранения энергии, так как система, получив извне теплоту Q1 могла бы совершить эквивалентное количество положительной внешней работы А = Q1 и вернуться в исходное состояние с тем же значением внутренней энергии.
Слайд 292. круговые процессы, в течение которых система только отдает теплоту, но
Тогда все элементарные количества теплоты были бы со знаком «минус», сумма была бы отлична от нуля. Т.е. отсутствовали бы
положительные члены этой суммы , соответствующие
получению тепла системой от окружающей среды отсутствовали бы.
Такие процессы также не противоречили бы закону сохранения энергии, так как работой внешних сил можно было бы полностью компенсировать убыль энергии системы от отдачи теплоты в окружающую среду (— А = — Q2), и система могла бы вернуться в исходное состояние с общим балансом энергии, равным нулю.
Слайд 30осуществить такой круговой процесс, в результате которого система полностью превращала бы
Пользуясь понятием коэффициента использования теплоты при круговых процессах
можно утверждать, что этот коэффициент никогда не может быть равен единице.
Слайд 31Пусть получение теплоты извне и отдача ее окружающим телам происходит изотермически.
или
т.
Для осуществления кругового процесса необходимо существование
разности температур между окружающими систему телами.
В результате прямого кругового процесса не только происходит превращение некоторого количества теплоты Q = Q1—Q2 в механическую работу, но обязательно имеет место «непроизводительный» переход теплоты Q2 от горячих тел к холодным.
Чем больше разность между температурой Т1, при которой система получает теплоту Q1 и температурой Т2, при которой отдается неиспользуемая теплота Q2, тем выше коэффициент полезного действия кругового процесса η= (Q1 — Q2)/Q1 = (Т1— T2)/T1 и, следовательно, тем меньше Q2.
Слайд 32В результате круговых процессов, идущих в обратном направлении, система получает теплоту
3. при круговом процессе увеличение энтропии системы от притока теплоты полностью компенсируется уменьшением энтропии от отдачи теплоты, и суммарное изменение энтропии равно нулю.
в каждом определенном равновесном состоянии система имеет вполне определенное значение энтропии.
Слайд 33Второе начало термодинамики
1) невозможны круговые процессы, в результате которых система только
2) круговые процессы, совершаемые любыми термодинамическими системами, сопровождаются получением некоторого количества теплоты Q1 от тел, имеющих высокие температуры, обязательной отдачей части этой теплоты Q2 телам, имеющим низкие температуры, и превращением разности Q1 — Q2 в механическую работу.
теплота связана с беспорядочным движением частиц системы, а механическая работа обусловлена упорядоченным движением этих частиц. Можно утверждать, что превращение теплоты в механическую работу есть переход энергии беспорядочного движения молекул системы в энергию упорядоченного движения. В связи с этим второй закон термодинамики можно понимать иначе:
3) при помощи круговых процессов, совершаемых какой-нибудь термодинамической системой, невозможно полностью превратить энергию беспорядочного теплового движения частиц окружающих тел в энергию упорядоченного движения самих этих тел
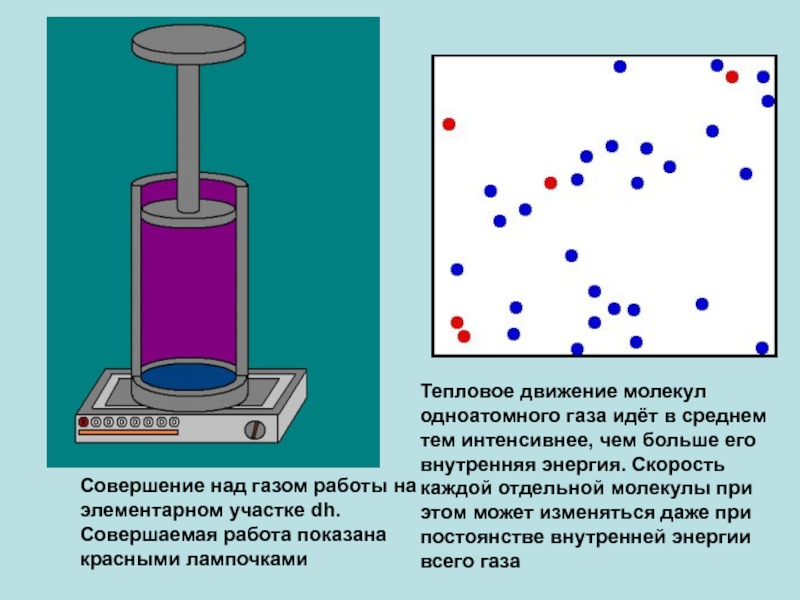
Слайд 34Совершение над газом работы на элементарном участке dh. Совершаемая работа показана
Тепловое движение молекул одноатомного газа идёт в среднем тем интенсивнее, чем больше его внутренняя энергия. Скорость каждой отдельной молекулы при этом может изменяться даже при постоянстве внутренней энергии всего газа
Слайд 35U2-U1=Q - A
Применяя это соотношение к круговым процессам, полагали U1= U2,
внутренняя энергия термодинамических систем есть однозначная функция состояния этих систем.
I начало термодинамики
при равновесном круговом процессе суммарное изменение энтропии термодинамических систем равно нулю, т. е., возвращаясь в исходное состояние, система приобретает в точности то же самое значение своей энтропии, которую она имела вначале.
4) энтропия термодинамической системы, находящейся в равновесном состоянии, есть однозначная функция этого состояния.
II начало термодинамики
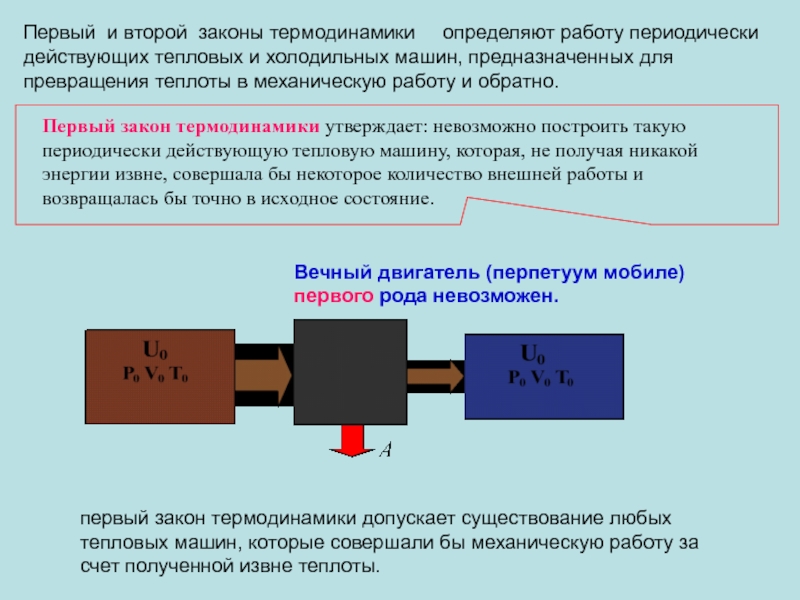
Слайд 36Первый и второй законы термодинамики определяют работу периодически действующих
Первый закон термодинамики утверждает: невозможно построить такую периодически действующую тепловую машину, которая, не получая никакой энергии извне, совершала бы некоторое количество внешней работы и возвращалась бы точно в исходное состояние.
Вечный двигатель (перпетуум мобиле) первого рода невозможен.
первый закон термодинамики допускает существование любых тепловых машин, которые совершали бы механическую работу за счет полученной извне теплоты.
Слайд 37
Q
=Q
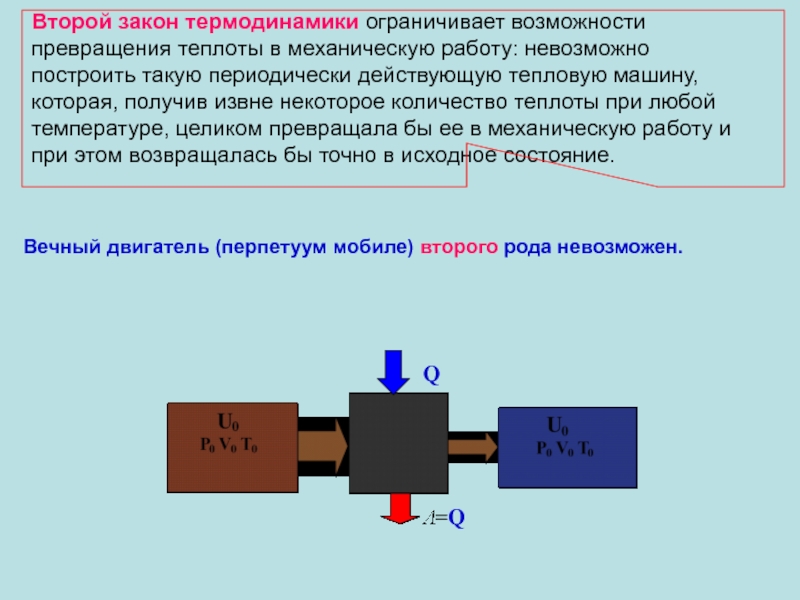
Второй закон термодинамики ограничивает возможности превращения теплоты в механическую работу: невозможно
Вечный двигатель (перпетуум мобиле) второго рода невозможен.
Слайд 39
Q1
=Q1-Q2
Q2
нагреватель
холодильник
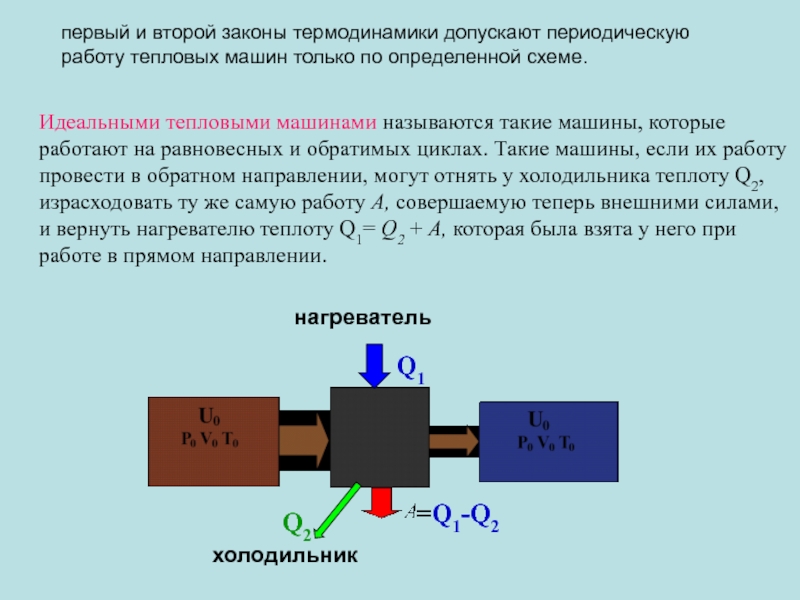
Идеальными тепловыми машинами называются такие машины, которые работают на равновесных и
первый и второй законы термодинамики допускают периодическую работу тепловых машин только по определенной схеме.
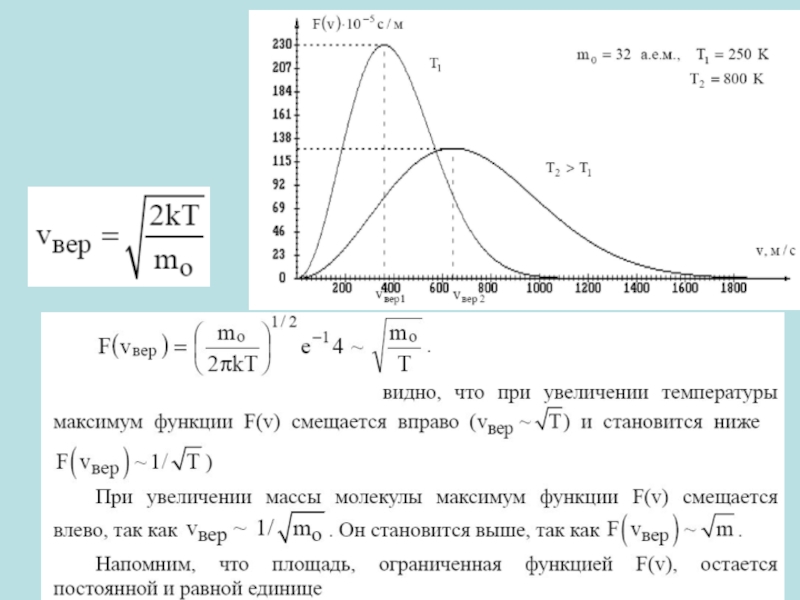
Слайд 40Можно показать, что при заданных температурах источника теплоты Т1 и холодильника
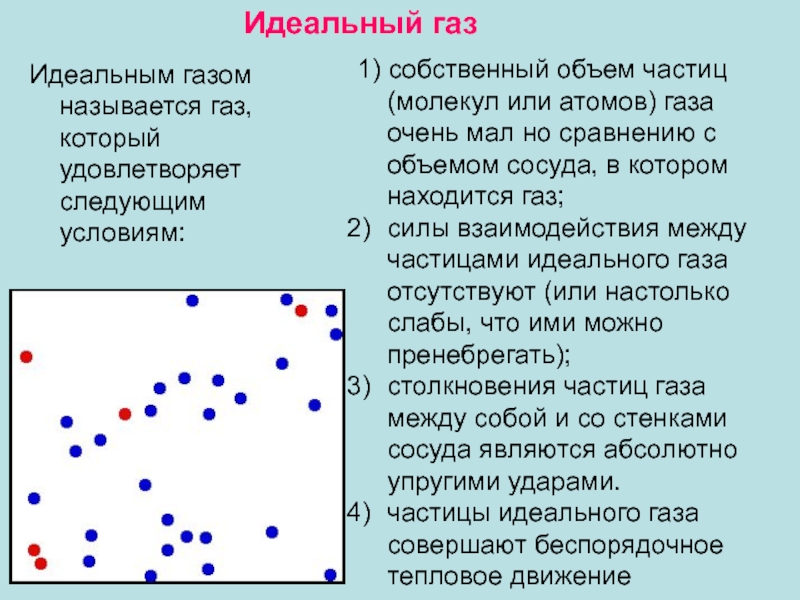
Слайд 42Идеальным газом называется газ, который удовлетворяет
Идеальный газ
1) собственный объем частиц (молекул или атомов) газа очень мал но сравнению с объемом сосуда, в котором находится газ;
силы взаимодействия между частицами идеального газа отсутствуют (или настолько слабы, что ими можно пренебрегать);
столкновения частиц газа между собой и со стенками сосуда являются абсолютно упругими ударами.
частицы идеального газа совершают беспорядочное тепловое движение
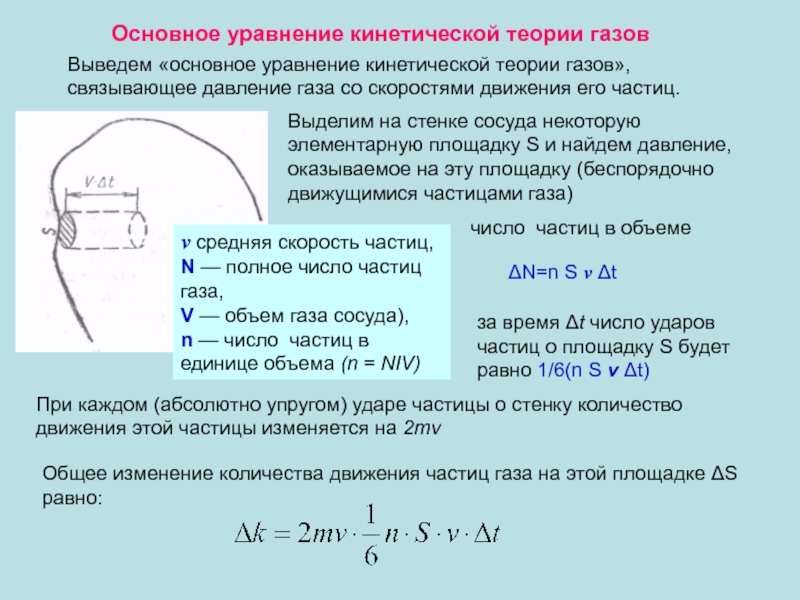
Слайд 43Выведем «основное уравнение кинетической теории газов», связывающее давление газа со скоростями
Основное уравнение кинетической теории газов
Выделим на стенке сосуда некоторую элементарную площадку S и найдем давление, оказываемое на эту площадку (беспорядочно движущимися частицами газа)
v средняя скорость частиц,
N — полное число частиц газа,
V — объем газа сосуда),
n — число частиц в единице объема (n = NIV)
ΔN=n S v Δt
за время Δt число ударов частиц о площадку S будет равно 1/6(n S v Δt)
число частиц в объеме
При каждом (абсолютно упругом) ударе частицы о стенку количество движения этой частицы изменяется на 2mv
Общее изменение количества движения частиц газа на этой площадке ΔS равно:
Слайд 44Согласно второму закону Ньютона, это изменение должно быть вызвано силой, приложенной
Тогда давление на газ, т. е. внешняя сила, действующая на газ со стороны единичной площадки, равна р = F/S
основное уравнение кинетической теории газов
n = N / V
Слайд 45Мы предполагали, что скорости молекул одинаковы; если же в газе имеются
vкв называется средней квадратичной скоростью молекул газа; она отличается от средней арифметической скорости
Теоретическое вычисление скоростей молекул основано на двух предположениях:
в газе не существует даже двух молекул, имеющих в точности одинаковые скорости;
число молекул ΔN, скорости которых лежат в узких пределах между v и v + Δv (например, от 100 до 101 м/с или от 500 до 501 м/с), прямо пропорционально общему числу молекул N, ширине интервала Δv и зависит от величины скорости и.
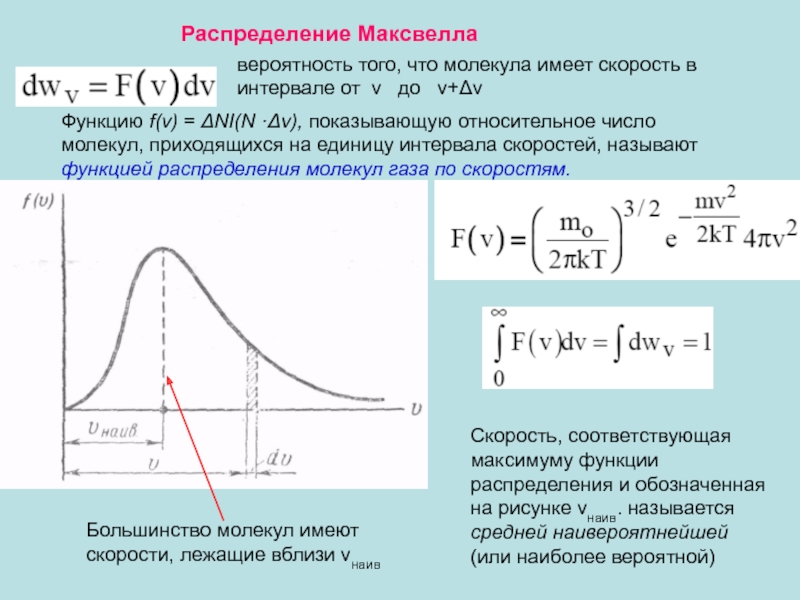
Слайд 46Функцию f(v) = ΔNI(N ·Δv), показывающую относительное число молекул, приходящихся на
Скорость, соответствующая максимуму функции распределения и обозначенная на рисунке vнаив. называется средней наивероятнейшей (или наиболее вероятной)
Большинство молекул имеют скорости, лежащие вблизи vнаив
вероятность того, что молекула имеет скорость в интервале от v до v+Δv
Распределение Максвелла
Слайд 48Уравнение состояния идеального газа
Пусть в объеме V при давлении р и
М = Nm
Количество газа
Число молекул в газе
Объем газа V (м2), давление p (Н/м2), температура T— по абсолютной шкале Кельвина
Измерения показали, что у газов при равновесных переходах из одного состояния в другое изменения параметров р, V и Т с некоторым приближением удовлетворяют объединенному закону Бойля—Мариотта и Гей-Люссака: для данной массы газа отношение произведения объема газа на его давление к абсолютной температуре сохраняется постоянным при переходе газа из одного равновесного состояния в другое:
идеальный газ определяется как такой газ, который в точности подчиняется законам Бойля—Мариотта и Гей-Люссака, а следовательно, объединенному закону
Слайд 49при данном р и Т V ~ М ~ N
k – коффициент пропорциональности
p V = N k T
p V = N k T=
уравнение состояния идеального газа (Клапейрона—Менделеева)
p V = N k T
разделим обе части на объем
давление газа прямо пропорционально числу молекул в единице объема и температуре газа.
Слайд 50Сравним уравнение
с основным уравнением кинетической теории газов
выражение для средней квадратичной
для 1 молекулы