- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Энергия движения твёрдого тела презентация
Содержание
- 1. Энергия движения твёрдого тела
- 2. 6.2.4. Энергия движения твёрдого тела.
- 3. Кинетическая энергия поступательного движения т.т.
- 4. Второе слагаемое.
- 5. Для центра масс…
- 6. Третье слагаемое.
- 7. Схема расчёта.
- 8. Полная энергия т.т.
- 9. Закон изменения полной энергии т.т.
- 10. 6.3.Столкновение (удар) тел. Определение. Удар называется неупругим,
- 11. Скорость тел после удара.
- 12. Выделение тепла.
- 13. Кинетическая энергия относительного движения тел.
- 14. Упругий удар.
- 15. Закон сохранения импульса и кинетической энергии.
- 16. Преобразование системы уравнений.
- 17. Преобразование системы уравнений.
- 18. Преобразование системы уравнений.
- 19. Решение системы уравнений.
- 20. Решение системы уравнений.
- 21. Анализ решения.
- 22. 7. Механика жидкостей и газов. 7.1. Кинематика
- 23. Определение газов. Определение. Газом называется система материальных
- 24. Давление.
- 25. Следствия из определения давления.
- 26. Поле давлений. Определение. Говорят, что в некотором
- 27. Поле скоростей.
- 28. Состояние жидкости. Если поле скоростей не зависит
- 29. Линия тока. В процессе течения частицы жидкости
- 30. Трубка тока. Выберем в пространстве некоторый контур
- 31. Свойство стенки трубки тока. Стенка трубки характерна
- 32. Закон сохранения числа частиц в потоке. Отсюда
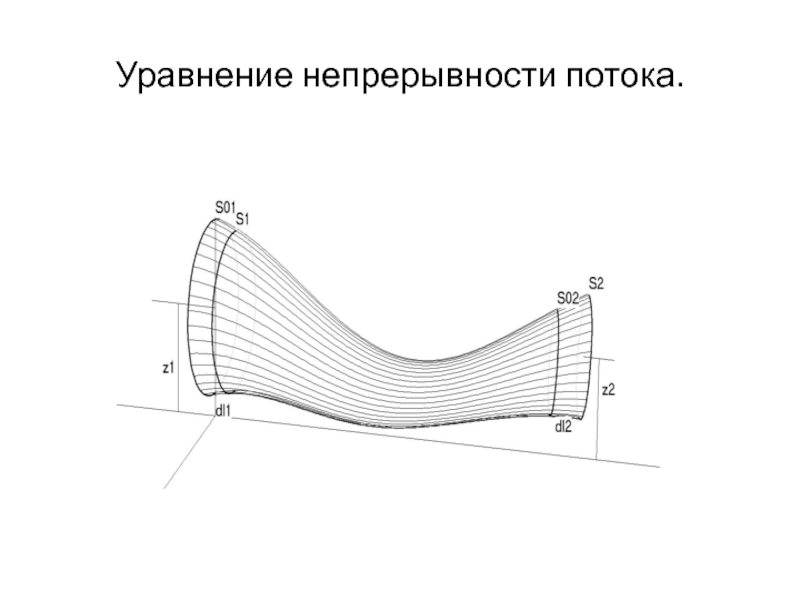
- 33. Уравнение непрерывности потока.
- 34. Перемещение сечений трубки тока.
- 35. Число вошедших и вышедших частиц.
- 36. Сохранение числа частиц.
- 37. Уравнение непрерывности.
- 38. Закон сохранения массы.
- 39. Уравнение непрерывности потока несжимаемой жидкости.
- 40. Демонстрация. Progr D: Progr E: Progr F: Progr G:
- 41. Расход жидкости. Определение. Объём жидкости, протекающий через
- 42. 7.2. Динамика жидкости. Закон Бернулли.
- 43. Энергия, приобретённая жидкостью.
- 44. Работа внешних сил.
- 45. Знак работы сил давления.
- 46. Закон изменения полной энергии для жидкости.
- 47. Применимость равенства. Здесь необходимо отметить, что в
- 48. Закон Бернулли.
- 49. Формулировка закона Бернулли. Прежде, чем сформулировать это
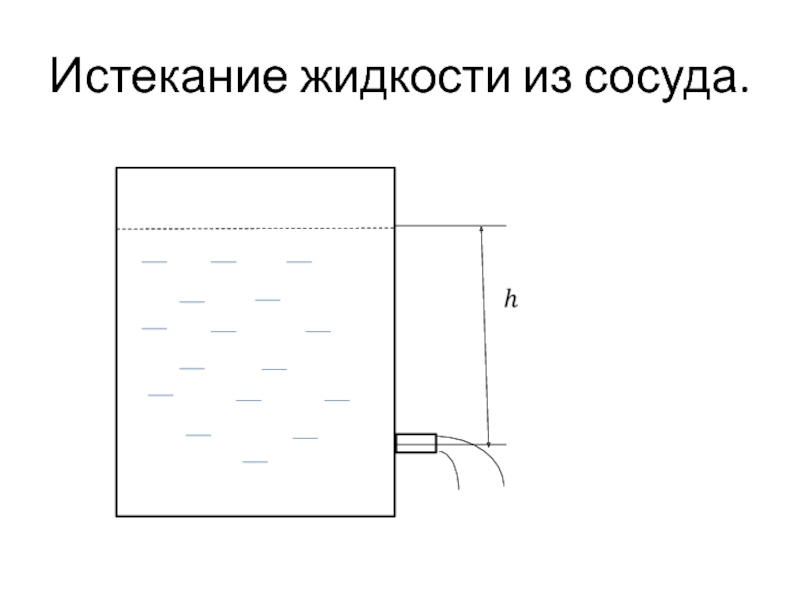
- 50. Истекание жидкости из сосуда.
- 51. Истекание воды из отверстия.
- 52. Скоростью уровня жидкости пренебрегаем.
- 53. Уравнение Бернулли для истекания жидкости.
- 54. Формула Торричелли.
- 55. 7.3. Гидростатическое давление. Закон Архимеда. Условие плавания тел.
- 56. Разность давлений на разных глубинах.
- 57. Гидростатическое давление.
- 58. Силы, действующие на боковые грани куба в жидкости.
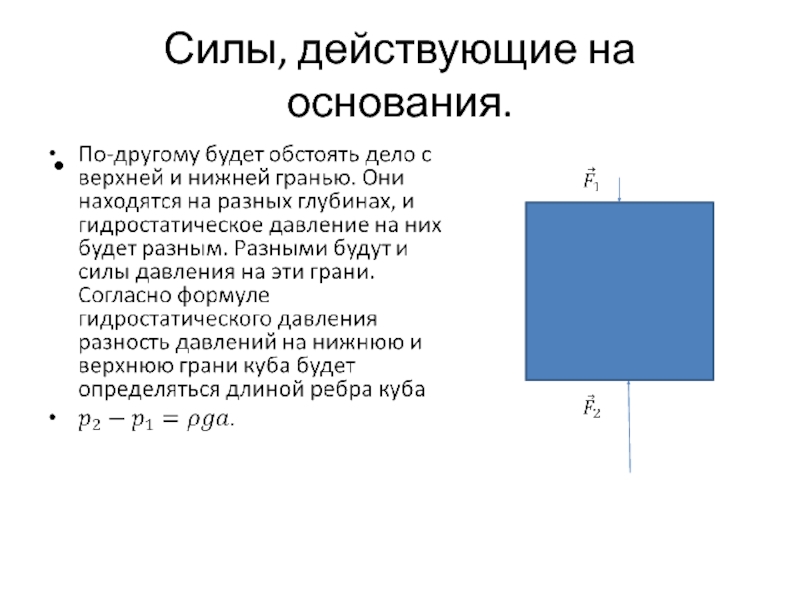
- 59. Силы, действующие на основания.
- 60. Выталкивающая сила.
- 61. Сила Архимеда.
- 62. Закон Архимеда. Это выражение и называется законом
- 63. Результирующая сила на тело в жидкости.
- 64. Условия плавания тел.
- 65. Объём части тела под поверхностью жидкости.
- 66. Безразличное равновесие.
- 67. 7.4. Внутреннее трение. Проведём мысленный эксперимент. По
- 68. Трение внутри жидкости.
- 69. Коэффициент внутреннего трения.
- 70. Внутреннее трение между бесконечно близкими слоями.
- 71. Схема расчёта
- 72. Сила трения
- 73. Баланс сил
- 74. Начальные условия
- 75. Поле скоростей
- 76. Схема расчёта расхода
- 77. Формула Пуазейля.
- 78. Сила вязкого трения.
- 79. Сила трения жидкости о трубу.
- 80. Формула Стокса.
Слайд 106.3.Столкновение (удар) тел.
Определение.
Удар называется неупругим, если после удара тела движутся вместе.
Расчёт
неупругого удара основан на законе сохранения импульса: импульс тел до удара равен импульсу тел после удара.
Слайд 227. Механика жидкостей и газов.
7.1. Кинематика жидкостей и газов. Уравнение непрерывности.
Определение.
Жидкостью называется система материальных точек, взаимодействие которых таково, что частицы могут перемещаться друг относительно друга, но число частиц в единице объёма жидкости остаётся неизменным.
Т.о. жидкость сохраняет свой объём, но не сохраняет своей формы. Она принимает форму сосуда, в который налита.
Т.о. жидкость сохраняет свой объём, но не сохраняет своей формы. Она принимает форму сосуда, в который налита.
Слайд 23Определение газов.
Определение. Газом называется система материальных точек, взаимодействие между которыми не
накладывает ограничений на взаимное перемещение частиц. Газы не сохраняют ни форму, ни объём.
Слайд 26Поле давлений.
Определение. Говорят, что в некотором пространстве задано поле давлений, если
каждой точке этой области поставлено в соответствие число, равное давлению в этой точке.
Слайд 28Состояние жидкости.
Если поле скоростей не зависит от времени, оно называется стационарным.
Течение в этом случае тоже называется стационарным.
Если скорость течения жидкости во всех точках пространства равна нулю, состояние называется статическим.
Если скорость течения жидкости во всех точках пространства равна нулю, состояние называется статическим.
Слайд 29Линия тока.
В процессе течения частицы жидкости или газа описывают некоторую кривую.
Определение.
Кривая, касательная в каждой точке к которой совпадает по направлению со скоростью течения жидкости или газа в этой точке, называется линией тока жидкости или газа.
Для стационарного течения линия тока совпадают с траекториями движения частиц в данной точке.
Для стационарного течения линия тока совпадают с траекториями движения частиц в данной точке.
Слайд 30Трубка тока.
Выберем в пространстве некоторый контур и через одну из его
точек проведём линию тока. Заставим точку обежать весь контур. Пространство, заключённое внутри поверхности, описанной этой линией тока, называется трубкой тока, а сама поверхность называется стенкой трубки тока.
Progr D: Progr E: Progr F: Progr G:
Progr D: Progr E: Progr F: Progr G:
Слайд 31Свойство стенки трубки тока.
Стенка трубки характерна тем, что частицы, находящиеся на
ней движутся по касательной к стенке и поэтому не могут её пересечь. Это значит, что зайти внутрь трубки тока или выйти из неё частицы могут только через основание трубки, но не через её стенки.
Слайд 32Закон сохранения числа частиц в потоке.
Отсюда следует, что в стационарном потоке
количество частиц, заключённых внутри трубки тока между неподвижными её основаниями, будет оставаться с течением времени величиной постоянной. Иначе говоря, сколько частиц внутрь трубки тока войдёт, столько за это же время из неё выйдет через другое основание. Это утверждение выражает закон сохранения числа частиц в потоке.
Слайд 41Расход жидкости.
Определение.
Объём жидкости, протекающий через поперечное сечение трубки тока за единицу
времени, называется расходом жидкости.
Поэтому уравнение непрерывности для несжимаемой жидкости можно ещё прочитать так: «Расход несжимаемой жидкости вдоль трубки тока во всех её сечениях одинаков».
Поэтому уравнение непрерывности для несжимаемой жидкости можно ещё прочитать так: «Расход несжимаемой жидкости вдоль трубки тока во всех её сечениях одинаков».
Слайд 47Применимость равенства.
Здесь необходимо отметить, что в балансе энергии не учитывалась тепловая
энергия, связанная с изменением плотности жидкости. Поэтому данное уравнение справедливо только для несжимаемой жидкости и не справедливо для газа.
Слайд 49Формулировка закона Бернулли.
Прежде, чем сформулировать это утверждение, заметим, что первое слагаемое
справа есть плотность кинетической энергии жидкости, второе – плотность потенциальной энергии, а последнее есть давление внутри жидкости. И так, уравнение Бернулли гласит: «Сумма плотности кинетической, потенциальной энергии жидкости и давления внутри жидкости есть величина неизменная вдоль линии тока».
Слайд 62Закон Архимеда.
Это выражение и называется законом Архимеда. Он гласит: «Выталкивающая сила,
действующая на тело со стороны жидкости, равна произведению плотности жидкости, ускорения свободного падения и объёма части тела, погружённой в жидкость и направлена в сторону противоположную ускорению свободного падения».
Слайд 677.4. Внутреннее трение.
Проведём мысленный эксперимент. По трубе течёт вода. Труба горизонтальна
и одинакового сечения.
Progr D: Progr E: Progr F: Progr G: Progr H:
Согласно закону Бернулли давление во всех точках трубки должно быть одинаковым, а манометрические трубки показывают падение давления в сторону течения жидкости.
Progr D: Progr E: Progr F: Progr G: Progr H:
Согласно закону Бернулли давление во всех точках трубки должно быть одинаковым, а манометрические трубки показывают падение давления в сторону течения жидкости.