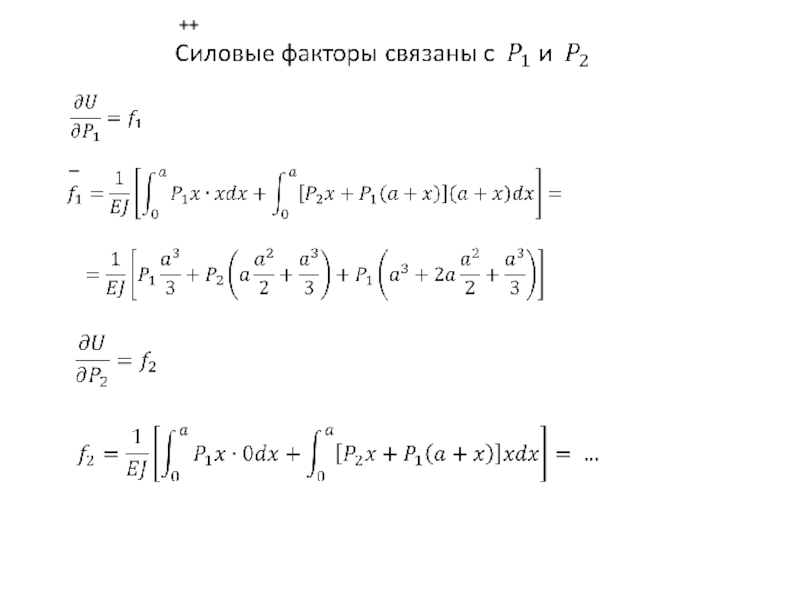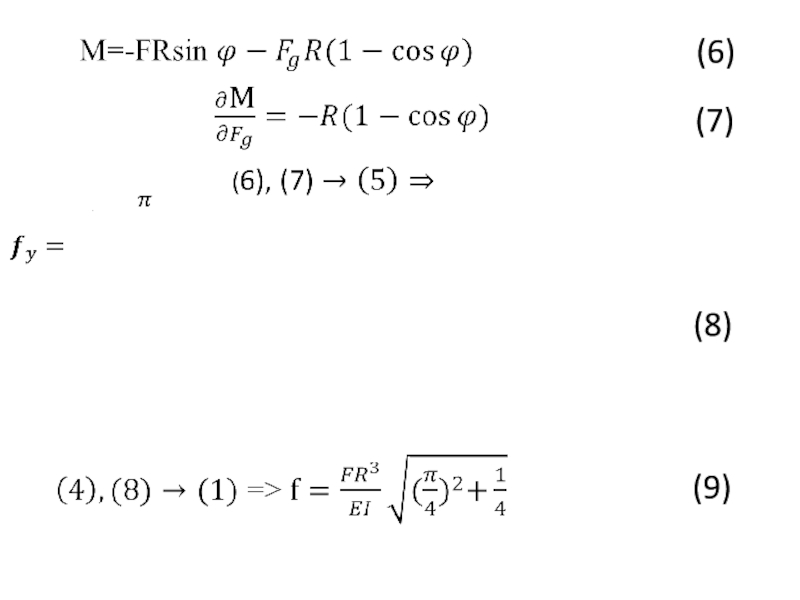- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Энергетические методы расчёта упругих систем презентация
Содержание
- 1. Энергетические методы расчёта упругих систем
- 2.
- 3. 1.ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ
- 6. 2. ЛИНЕЙНО УПРУГИЕ СИСТЕМЫ. ЗАКОН
- 7. Приложен момент М0 затем – сила
- 8. Коэффициенты
- 9. Работа внешних сил не зависит от порядка
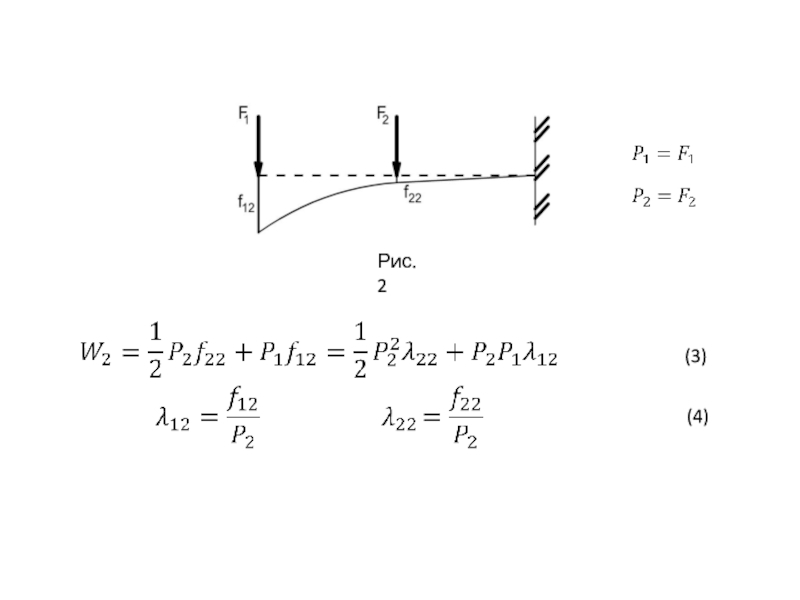
- 10. (3) (4) Рис.2
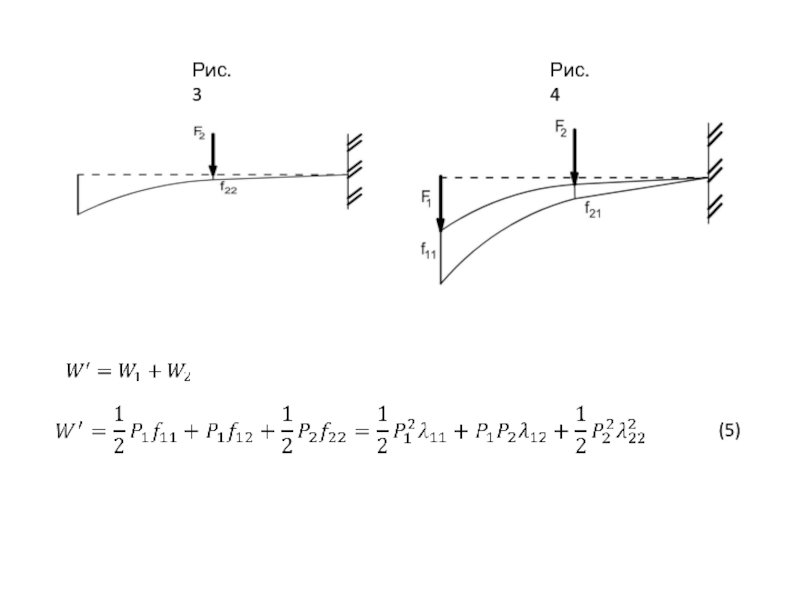
- 11. (5) Рис.3 Рис.4
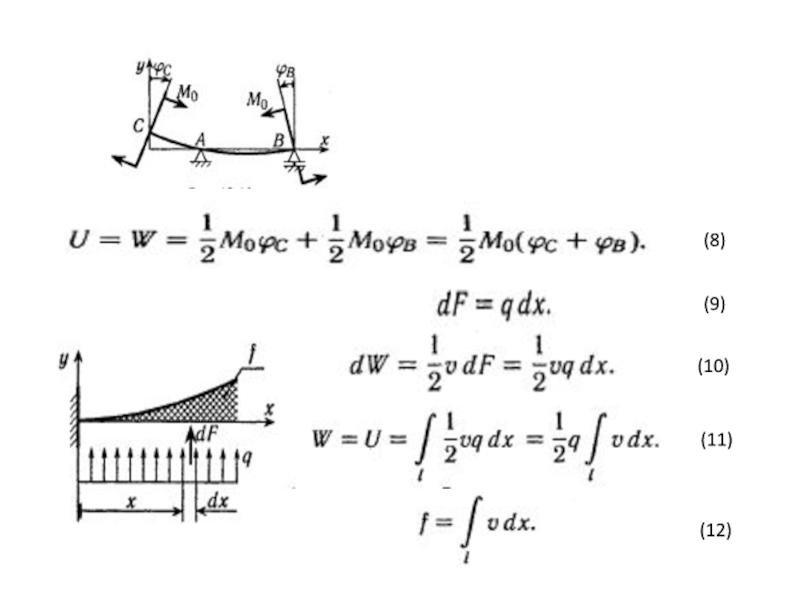
- 12. (8) (9) (10) (11) (7) (6)
- 13. (12) Теорема Клайперона (13) Потенциальная энергия
- 14. (1) (2) (3) (4) (5) y
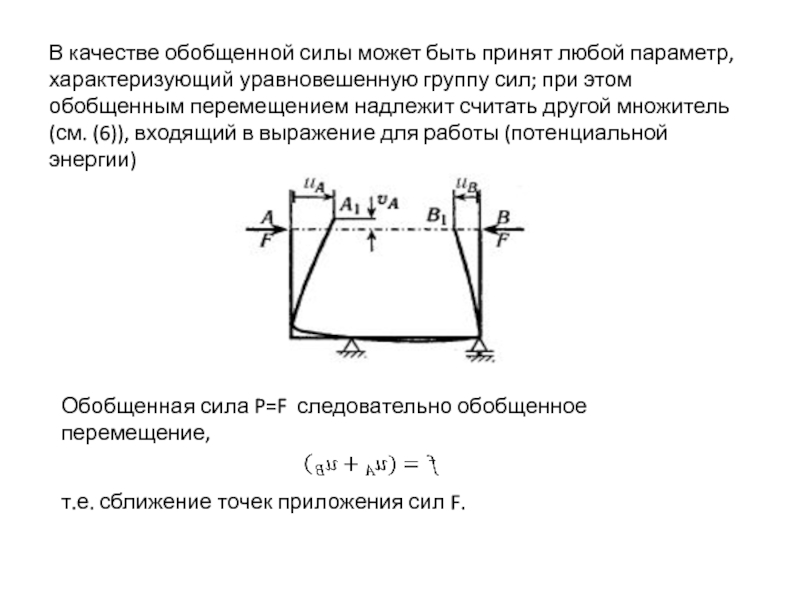
- 15. В качестве обобщенной силы может быть принят
- 16. (8) (9) (10) (11) (12)
- 17. Если
- 18. (7) (8) (9) Теорема Л. Лагранжа:
- 19. ТЕОРЕМА КАСТИЛЬЯНО .
- 20. Вводится понятие приращения дополнительной работы (дополнительной энергии)
- 21. Если на упругую систему действуют n
- 22. Для линейных систем .
- 23. В случае плоского изгиба Величины
- 24. Дифференцирование сложной функции Для
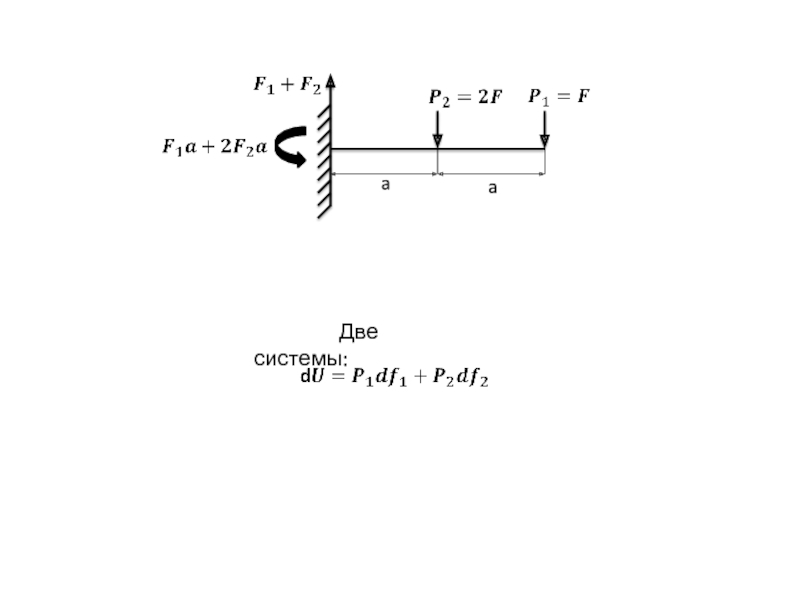
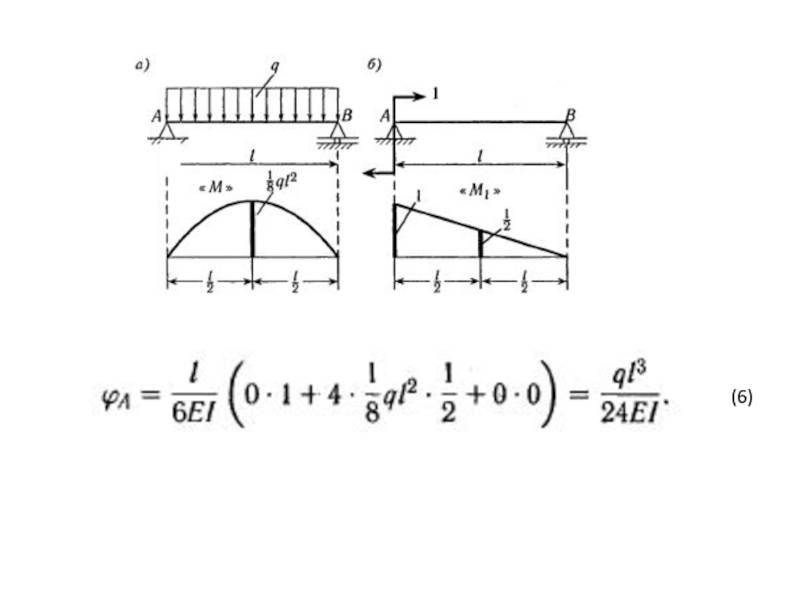
- 25. a) Рис. а. Определить вертикальное перемещение yB
- 26. a a
- 27. a a
- 28. ++ _
- 29. б) Рис. б. Определить угол поворота φВ
- 30. Реакции, эпюра изгибающего момента, примерный вид
- 31. По теореме Кастильяно:
- 32. По теореме Кастильяно: (24) (25) (26)
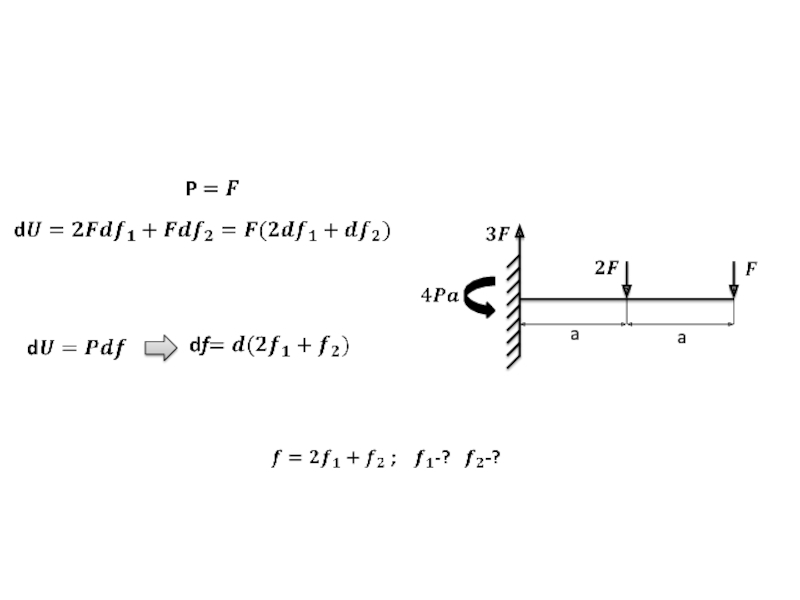
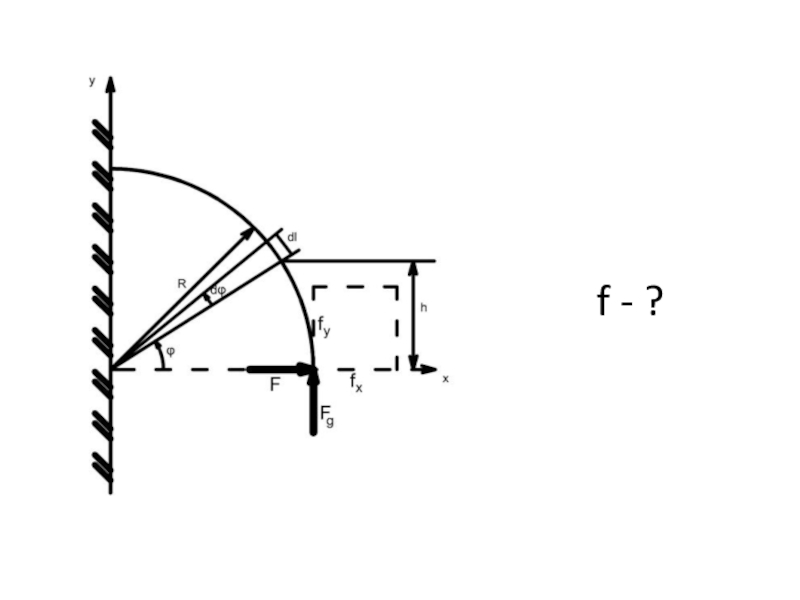
- 33. f - ?
- 34. (1) (2) Правило знаков для изгибающих
- 35. (3) Для вычисления вертикальных перемещений
- 36. (8) (9) (6) (7)
- 37. Эквивалентно (1) 7.Формула Максвелла-Мора (15')
- 38. (2) Дж. Максвелл и О. Мор (3) (4)
- 39. 3 (4) (3) (4) (3) (3)
- 41. (5)
- 42. (6)
- 43. СПАСИБО ЗА ВНИМАНИЕ!
- 44.
- 46. Обобщенные силы и обобщенные перемещения
Слайд 31.ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ
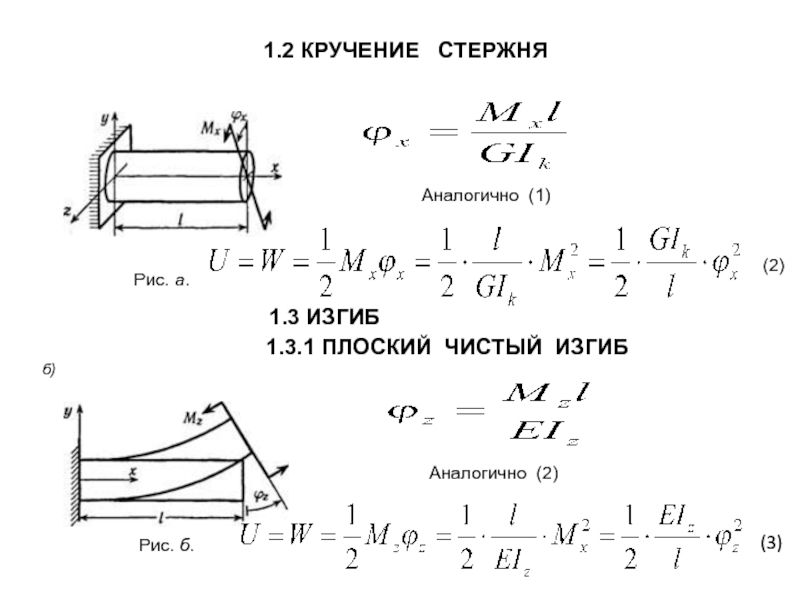
1.1 РАСТЯЖЕНИЕ ( СЖАТИЕ ) СТЕРЖНЯ
Рис.а
Рис. б.
Слайд 4
а)
Аналогично (1)
(2)
1.3 ИЗГИБ
б)
1.3.1 ПЛОСКИЙ ЧИСТЫЙ ИЗГИБ
Аналогично (2)
Рис. а.
Рис. б.
(3)
Слайд 5
Mz(x) ≠ const.
Соотношение (3) применимо к участку длинной dx
Вклад в потенциальную энергию упругой деформации вносит поперечная сила Qy
где ky – коэффициент формы поперечного сечения балки.
В случае сложного изгиба с кручением и растяжением-сжатием
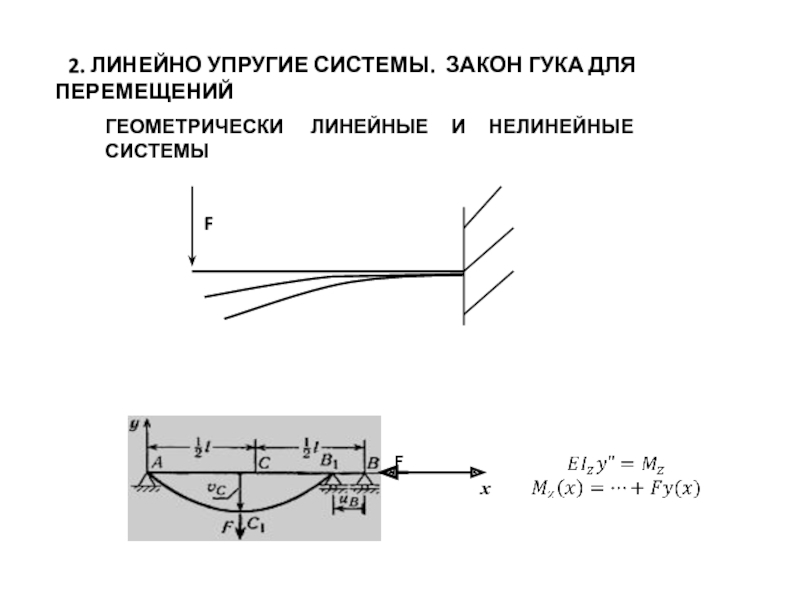
Слайд 6 2. ЛИНЕЙНО УПРУГИЕ СИСТЕМЫ. ЗАКОН ГУКА ДЛЯ ПЕРЕМЕЩЕНИЙ
ГЕОМЕТРИЧЕСКИ
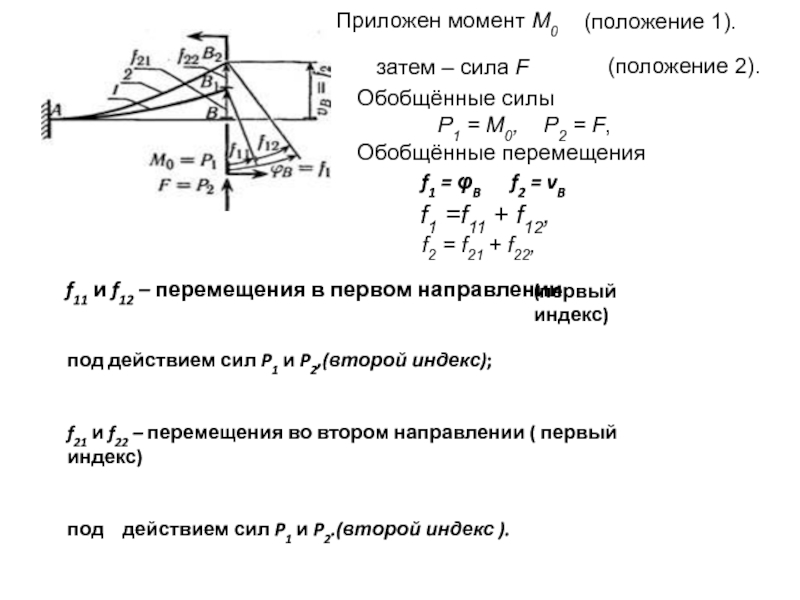
Слайд 7Приложен момент М0
затем – сила F
(положение 2).
Обобщённые силы
P1 = M0, P2 = F,
Обобщённые перемещения
f1 = φB f2 = vB
f1 =f11 + f12,
f2 = f21 + f22,
f11 и f12 – перемещения в первом направлении
под действием сил P1 и P2,(второй индекс);
f21 и f22 – перемещения во втором направлении ( первый индекс)
под действием сил P1 и P2.(второй индекс ).
(первый индекс)
Слайд 8 Коэффициенты податливости
,
,
,
.
При действии n обобщённых
Далее будет доказано:
.
Слайд 13
(12)
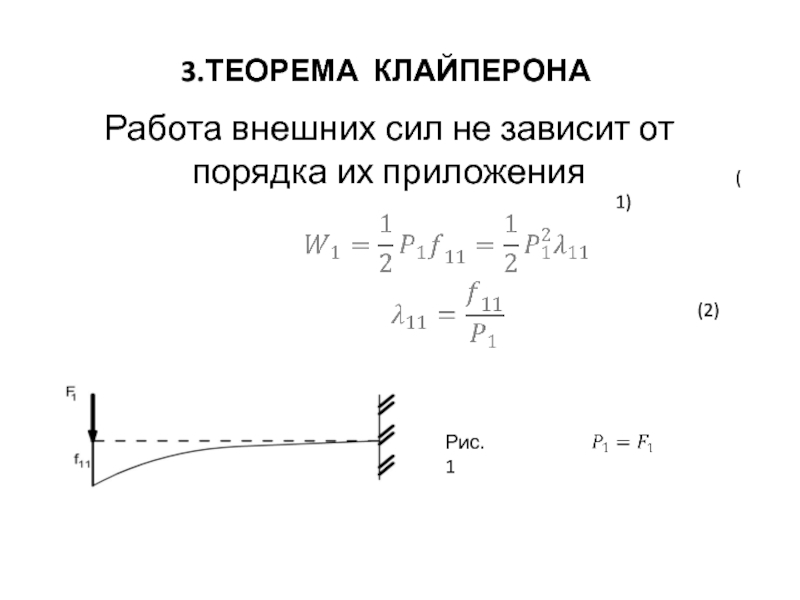
Теорема Клайперона
(13)
Потенциальная энергия линейной упруго-деформируемой системы равна половине суммы произведений обобщенных
Слайд 14(1)
(2)
(3)
(4)
(5)
y
(6)
Пример Р характеризует систему взаимно уравновешенных сил:
(7)
4.Обобщенные силы и обобщенные
y
Слайд 15В качестве обобщенной силы может быть принят любой параметр, характеризующий уравновешенную
Обобщенная сила P=F следовательно обобщенное перемещение,
т.е. сближение точек приложения сил F.
Слайд 18(7)
(8)
(9)
Теорема Л. Лагранжа:
Обобщенная сила равна частной производной от потенциальной энергии упругой
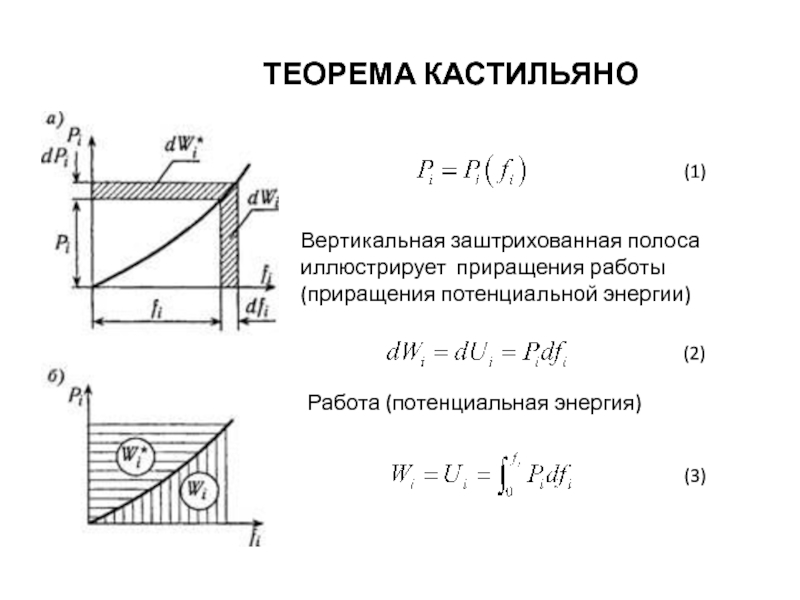
Слайд 19ТЕОРЕМА КАСТИЛЬЯНО
.
Вертикальная заштрихованная полоса иллюстрирует приращения работы (приращения потенциальной энергии)
Работа
(1)
(2)
(3)
Слайд 20Вводится понятие приращения дополнительной работы (дополнительной энергии)
горизонтальная заштрихованная полоса (
См. рисунок
(4)
(5)
(6)
Слайд 21 Если на упругую систему действуют n сил, то полный дифференциал
(4), (8) ⟹
частная производная от дополнительной энергии U* по обобщённой силе Pi равна обобщённому перемещению fi, соответствующему этой силе
(7)
(8)
(9)
Если dPi ≠ 0, а все остальные приращения сил равны нулю
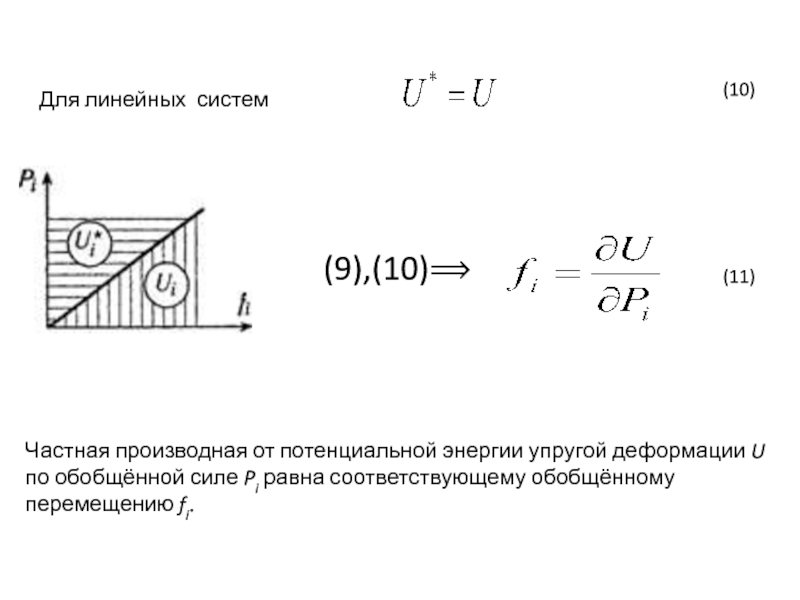
Слайд 22Для линейных систем
.
Частная производная от потенциальной энергии упругой деформации U
(9),(10)⟹
(10)
(11)
Слайд 23В случае плоского изгиба
Величины Pi и x взаимно независимы, операции
Множитель dx/2EIz не зависит от силы Pi
(12)
(13)
(14)
Слайд 24 Дифференцирование сложной функции
Для изгиба с кручением, растяжением-сжатием и сдвигом
(15)
(16)
(17)
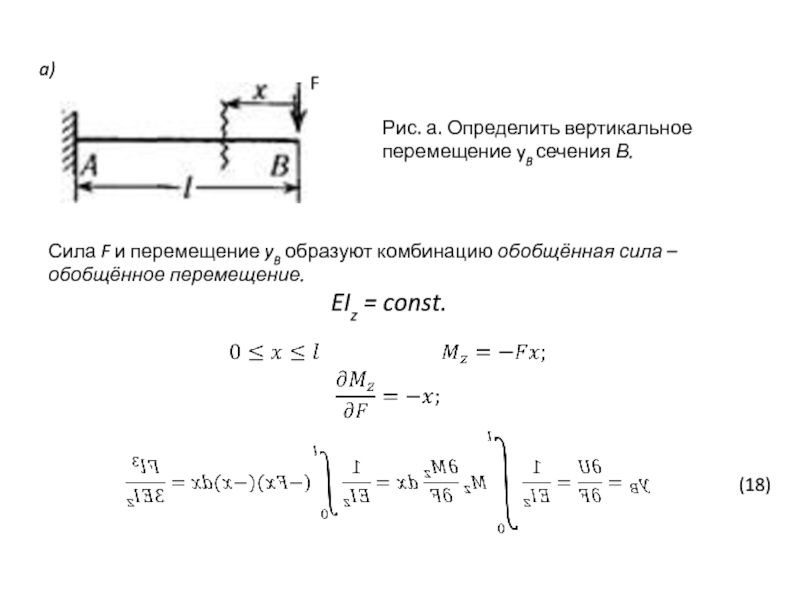
Слайд 25a)
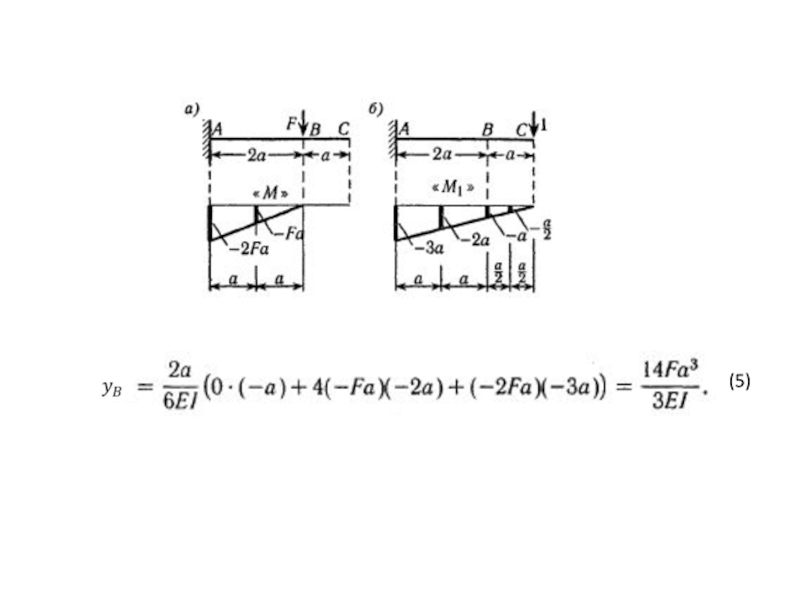
Рис. а. Определить вертикальное перемещение yB сечения В.
Сила F и перемещение
EIz = const.
(18)
F
Слайд 29б)
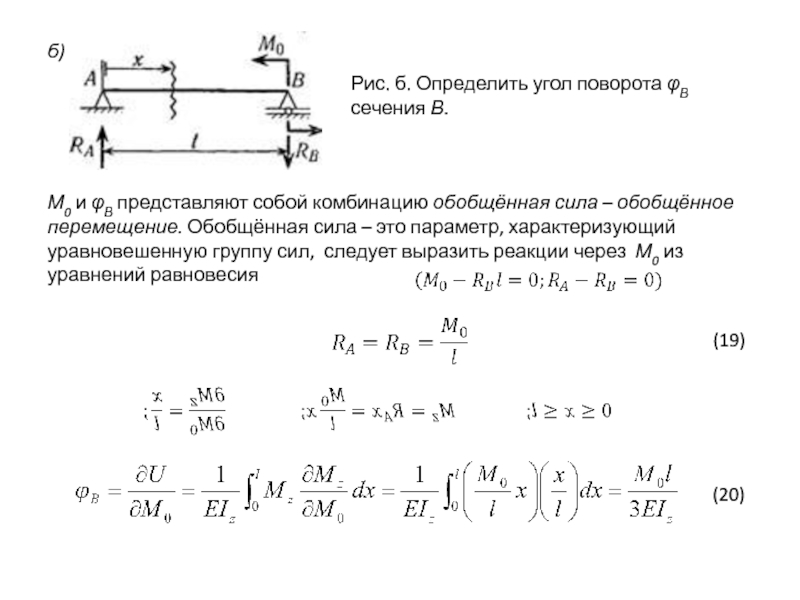
Рис. б. Определить угол поворота φВ сечения В.
М0 и φВ
(19)
(20)
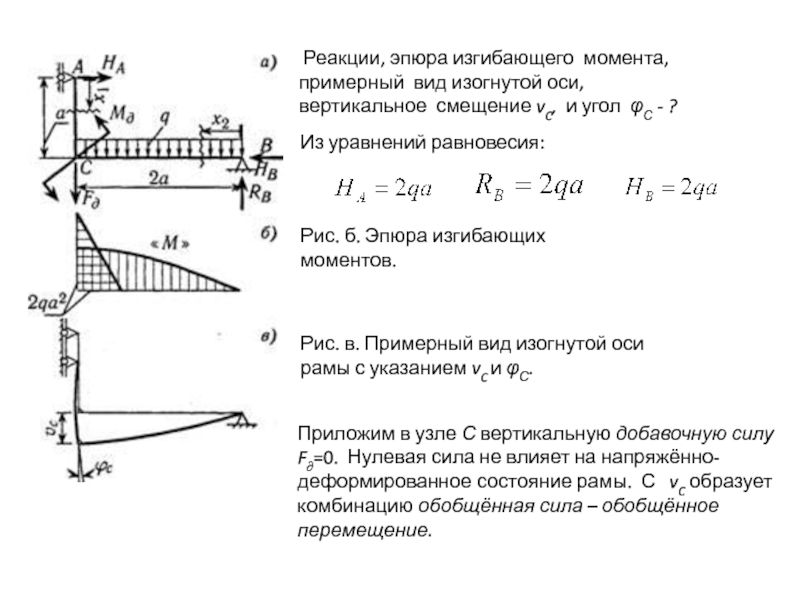
Слайд 30 Реакции, эпюра изгибающего момента, примерный вид изогнутой оси, вертикальное смещение
Из уравнений равновесия:
Рис. б. Эпюра изгибающих моментов.
Рис. в. Примерный вид изогнутой оси рамы с указанием vC и φС.
Приложим в узле С вертикальную добавочную силу F∂=0. Нулевая сила не влияет на напряжённо-деформированное состояние рамы. С vC образует комбинацию обобщённая сила – обобщённое перемещение.
Слайд 31
По теореме Кастильяно:
Приложим в узле С добавочный момент М∂ =
(21)
(22)
(23)
Слайд 34
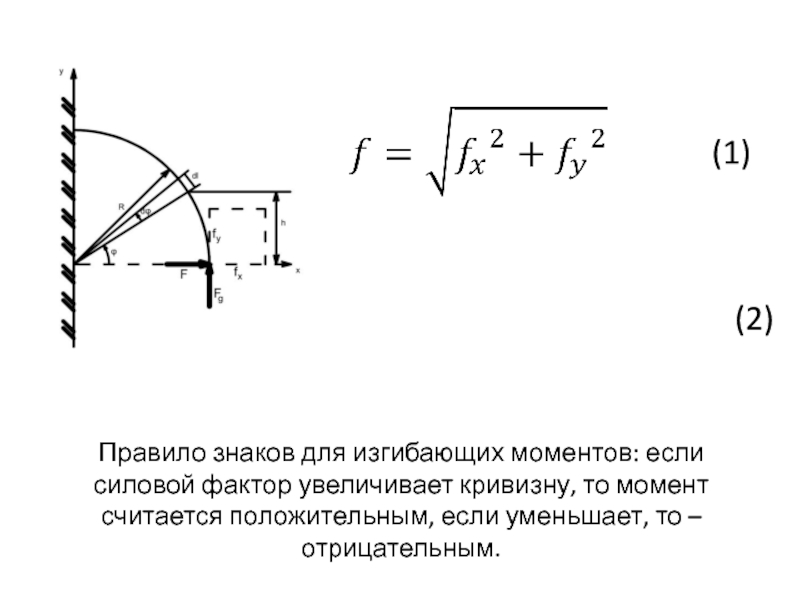
(1)
(2)
Правило знаков для изгибающих моментов: если силовой фактор увеличивает кривизну, то
Слайд 35
(3)
Для вычисления вертикальных перемещений приложим добавочную силу Fg , соответствующую fy
(4)
(5)
Слайд 45 2.ЛИНЕЙНО
ЗАКОН ГУКА ДЛЯ ПЕРЕМЕЩЕНИЙ
F
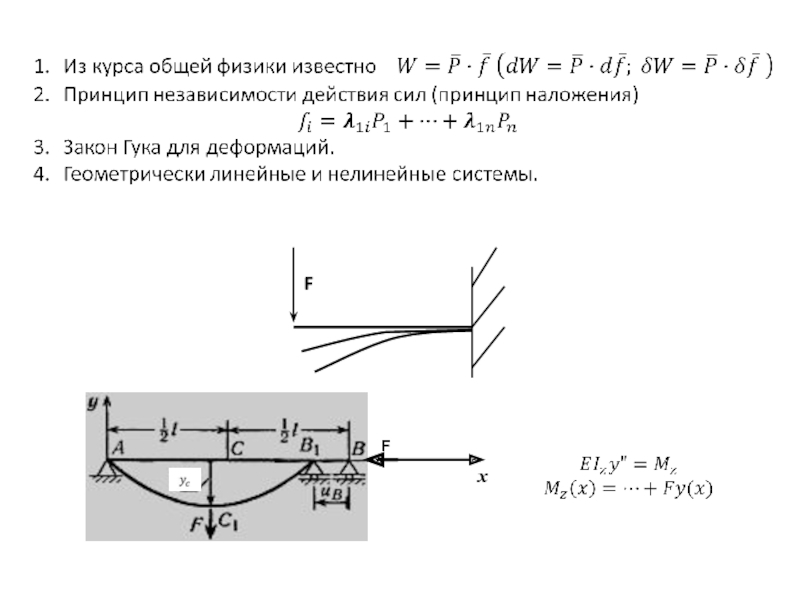
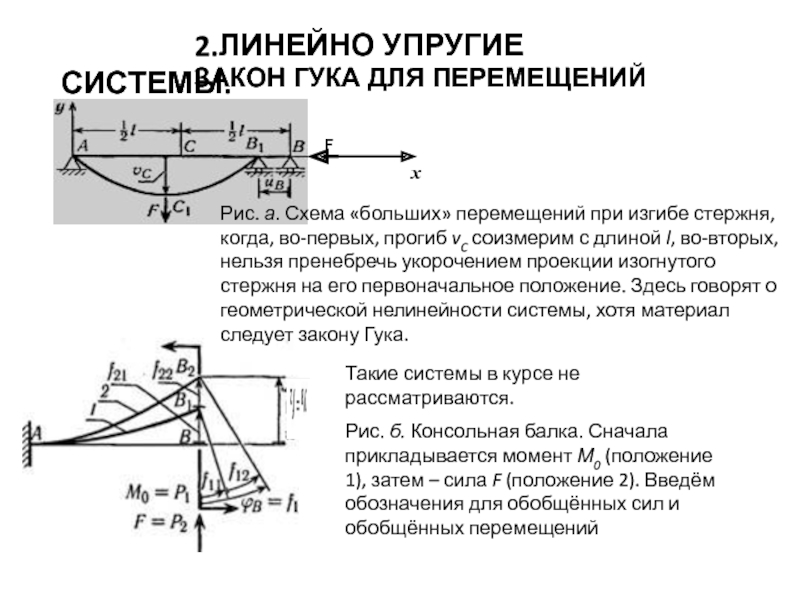
Рис. а. Схема «больших» перемещений при изгибе стержня, когда, во-первых, прогиб vC соизмерим с длиной l, во-вторых, нельзя пренебречь укорочением проекции изогнутого стержня на его первоначальное положение. Здесь говорят о геометрической нелинейности системы, хотя материал следует закону Гука.
Такие системы в курсе не рассматриваются.
Рис. б. Консольная балка. Сначала прикладывается момент М0 (положение 1), затем – сила F (положение 2). Введём обозначения для обобщённых сил и обобщённых перемещений
x