- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы специальной теории относительности презентация
Содержание
- 1. Элементы специальной теории относительности
- 2. Некоторые эксперименты с “драматическими” результатами a) Заряженная
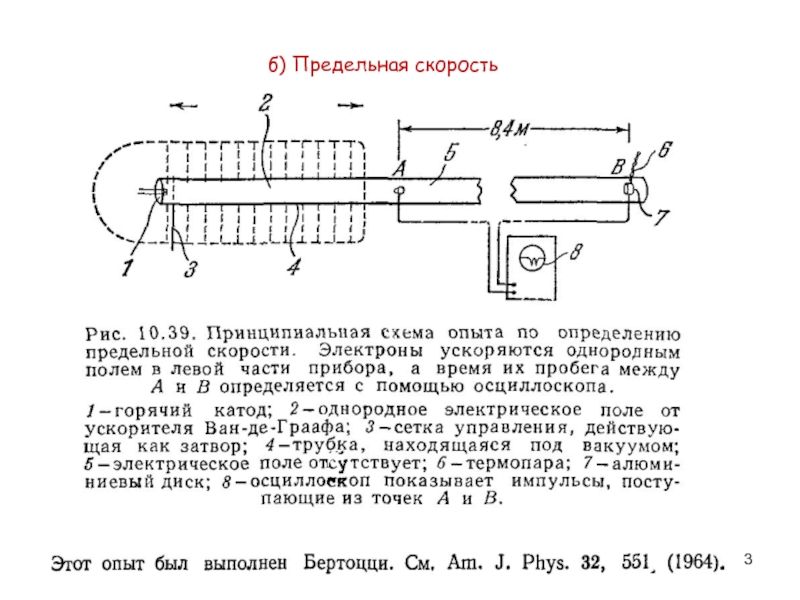
- 3. б) Предельная скорость
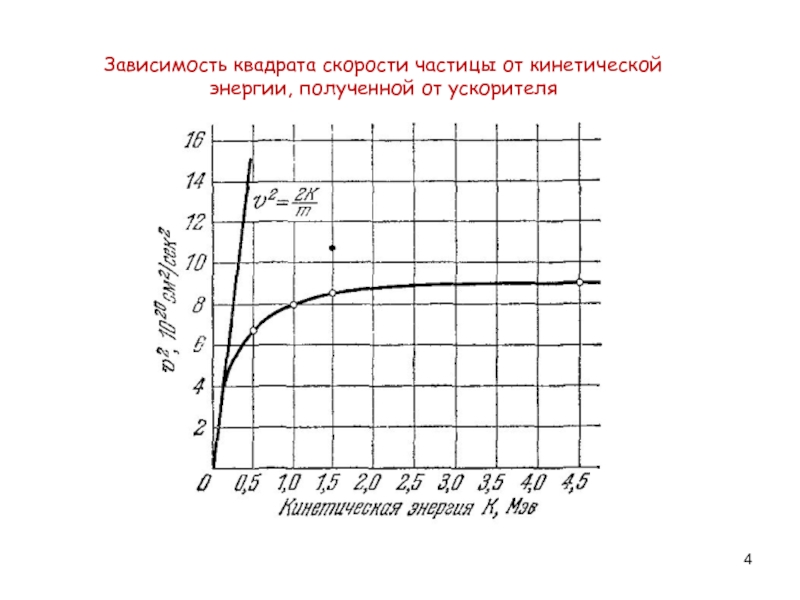
- 4. Зависимость квадрата скорости частицы от кинетической энергии, полученной от ускорителя
- 5. в) Опыт Майкельсона и Морли (1887 г).
- 6. II. Преобразования Лоренца Рассмотрим поверхность фронта световой
- 7. Сложение скоростей Частные случаи, ломающие мировоззрение:
- 8. Преобразование длин и временных интервалов
- 9. III. Что же там на самом деле
- 10. Будем последовательны и наложим руки на энергию!
- 11. Ну вот, мы и собрали “вершки” с
Слайд 1Элементы специальной теории относительности
(СТО)
Лекция 10
(Пространство и время в кинематике)
Слайд 2Некоторые эксперименты с “драматическими” результатами
a) Заряженная частица и провод с током
В
лабораторной системе провод не заряжен,
но в нем существует ток i, который создает
магнитное поле, в котором на частицу действует
сила Лоренца, заставляющая притягиваться
частицу к проводу.
НО! В системе, связанной с частицей этой
силы НЕТ! Так как частица покоится!
Как же так? Выходит, что факт притяжения
(или его отсутствия) зависит от точки зрения
наблюдателя. НЕ МОГУ С ЭТИМ СМИРИТЬСЯ!
но в нем существует ток i, который создает
магнитное поле, в котором на частицу действует
сила Лоренца, заставляющая притягиваться
частицу к проводу.
НО! В системе, связанной с частицей этой
силы НЕТ! Так как частица покоится!
Как же так? Выходит, что факт притяжения
(или его отсутствия) зависит от точки зрения
наблюдателя. НЕ МОГУ С ЭТИМ СМИРИТЬСЯ!
Слайд 6II. Преобразования Лоренца
Рассмотрим поверхность фронта световой волны от точечного
источника света,
находящегося в начале координат. Это сфера
и ее уравнение:
Но в другой системе (двигающейся со скоростью ) скорость света
такая же, следовательно и уравнение такое же:
Если преобразования Галилея верны, то какое-то из этих уравнений
точно не верно! Действительно, если подставить преобразования:
получим:
Но, если положить, что
То:
А вот это подойдет:
и ее уравнение:
Но в другой системе (двигающейся со скоростью ) скорость света
такая же, следовательно и уравнение такое же:
Если преобразования Галилея верны, то какое-то из этих уравнений
точно не верно! Действительно, если подставить преобразования:
получим:
Но, если положить, что
То:
А вот это подойдет:
Слайд 9III. Что же там на самом деле в динамике?
Если импульс по-прежнему
будем определять как
то при переходе в другую “быструю” инерциальную систему он
сохраняться не будет!!!
Выполнение закона сохранения количества движения можно
обеспечить лишь приняв, что:
Эх, не побоимся и признаем, что:
Тогда понятен результат
эксперимента Бертоцци!
то при переходе в другую “быструю” инерциальную систему он
сохраняться не будет!!!
Выполнение закона сохранения количества движения можно
обеспечить лишь приняв, что:
Эх, не побоимся и признаем, что:
Тогда понятен результат
эксперимента Бертоцци!
Слайд 10Будем последовательны и наложим руки на энергию!
Так как:
то:
После подстановки получим: или:
Здесь ПОЛНАЯ энергия:
Кроме кинематического есть и другой инвариант:
После подстановки получим: или:
Здесь ПОЛНАЯ энергия:
Кроме кинематического есть и другой инвариант:
Слайд 11Ну вот, мы и собрали “вершки” с механики.
Со следующего раза начнем
мучить молекулярную физику.