Элементы линейной алгебры в электротехнике (электронное учебное пособие) презентация

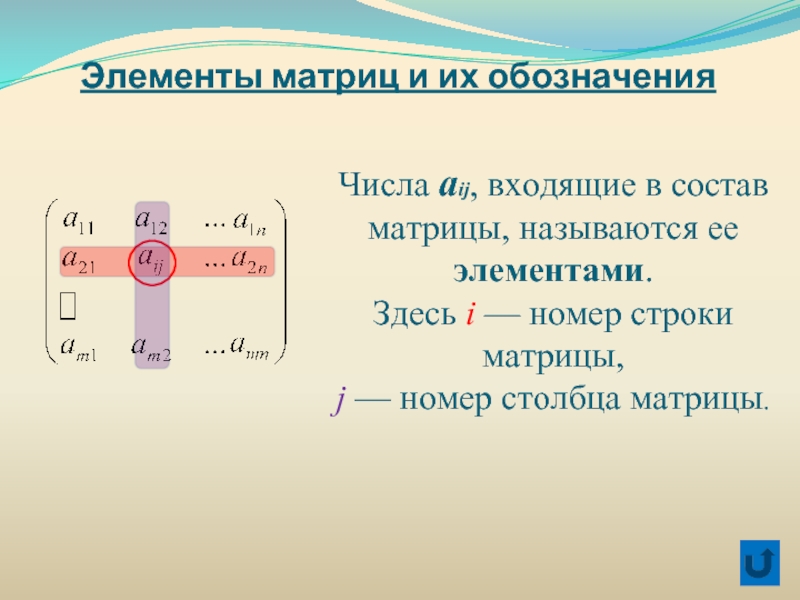
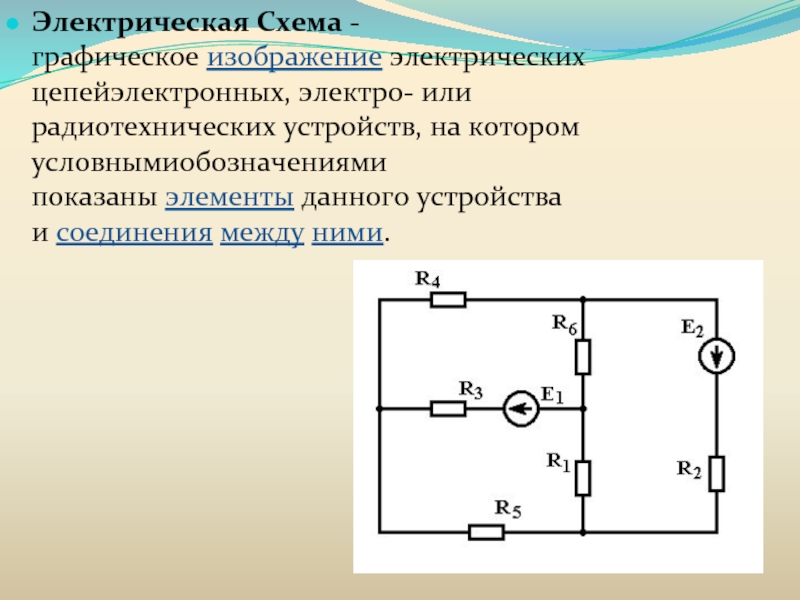
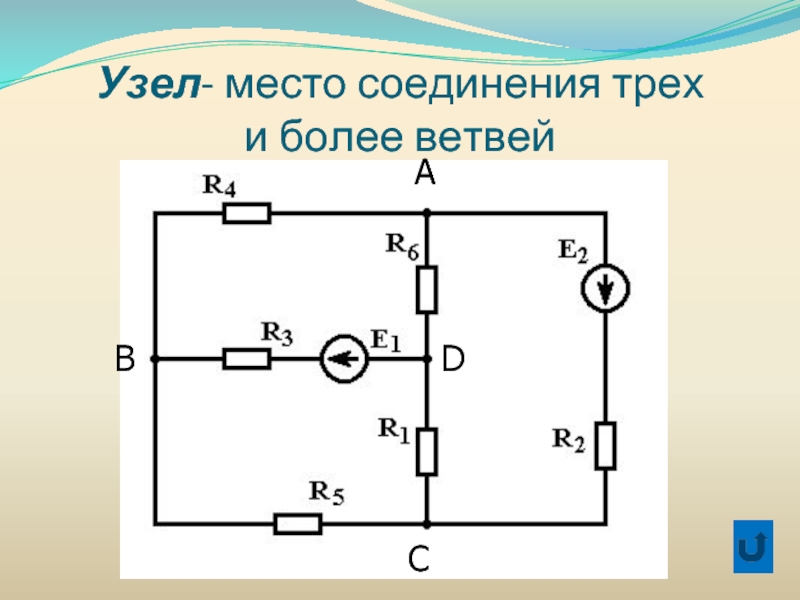
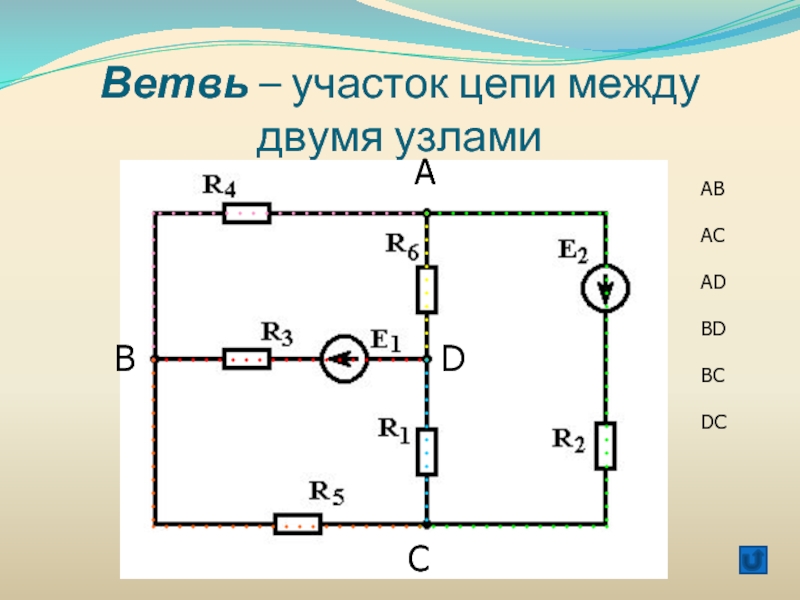
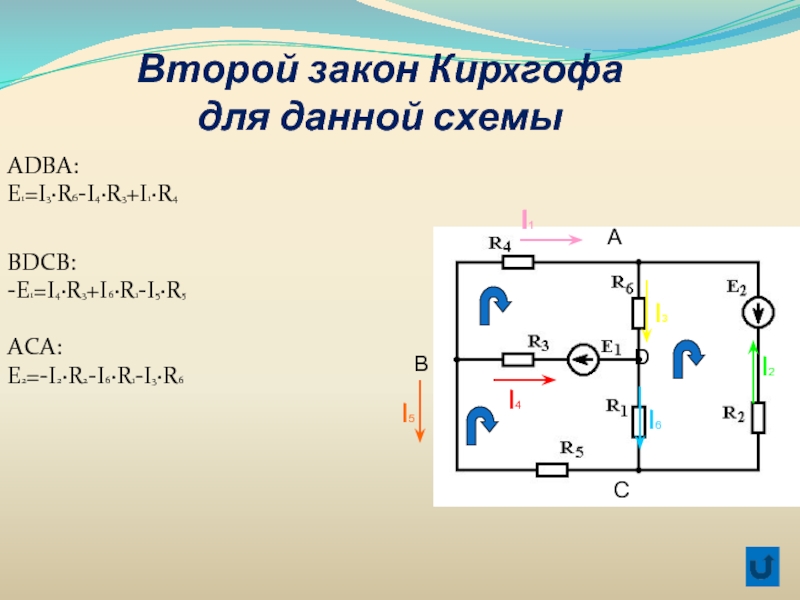
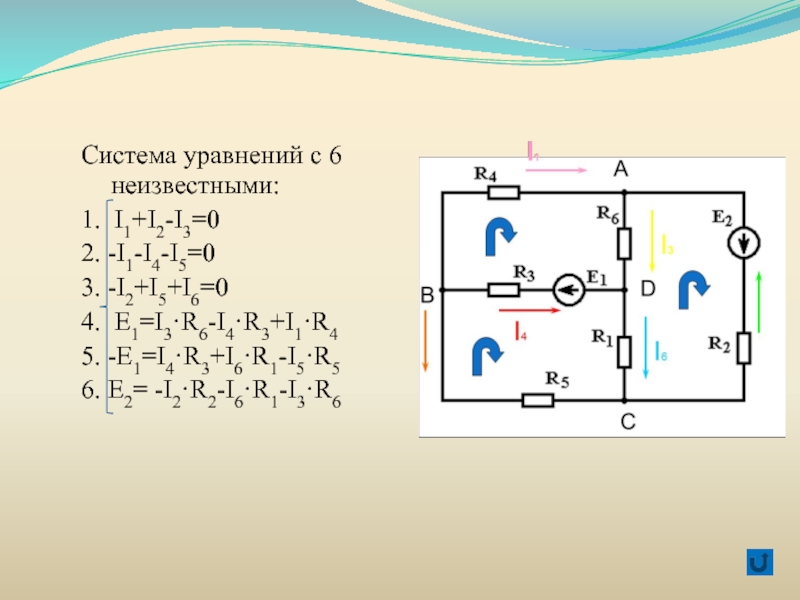
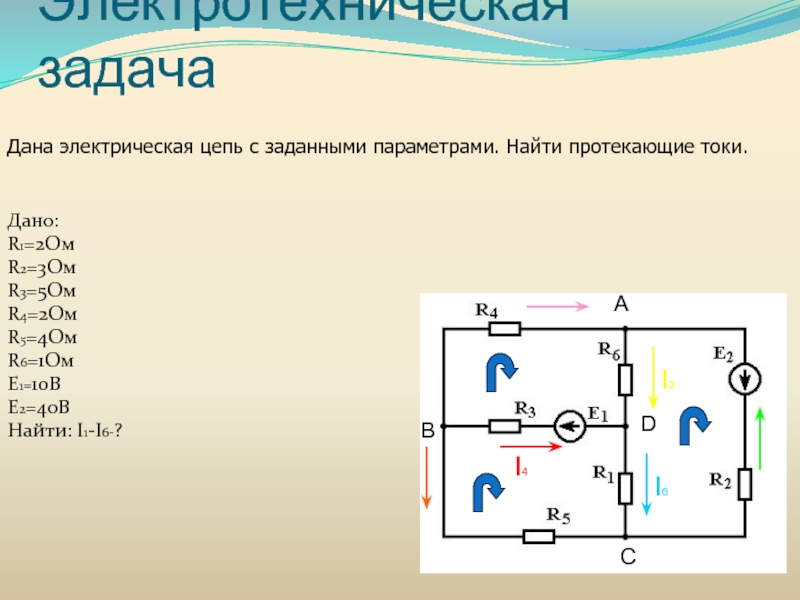
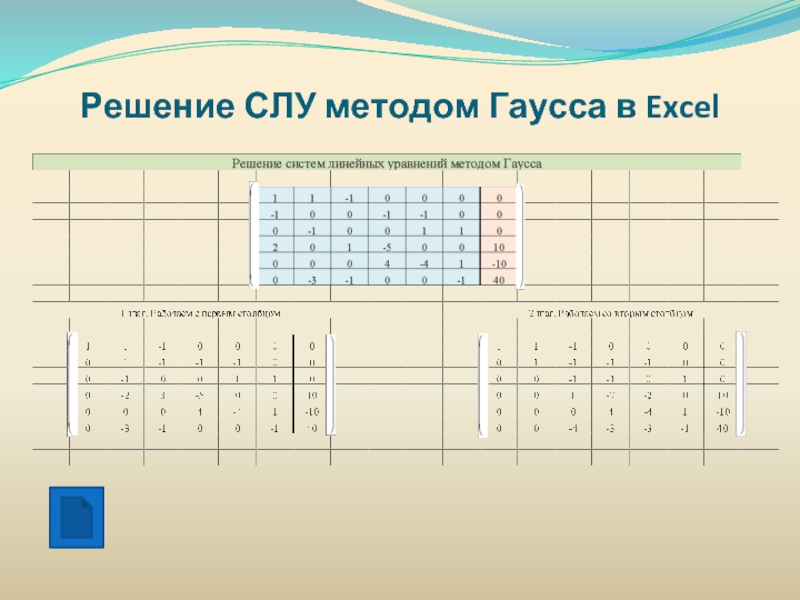
Элементы линейной алгебры в электротехнике
(электронное учебное пособие)

Руководители: Касаткина Инга Сергеевна, преподаватель математики
Никитина Наталья Васильевна, преподаватель спецдисциплин

БОУ СПО УР «Ижевский индустриальный техникум»

г. Ижевск, 2013

Для краткого обозначения матрицы используется большая латинская буква, например A или символ (aij) 

A= (aij) (i=1,2,…,m; j=1,2,…,n;)

Для квадратной матрицы определено понятие диагоналей

Частные случаи

Частные случаи

Например:

Например:

Например:

Например:

Свойства сложения

Например:

Например:

Например:

Умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В

Свойства умножения

Круг его интересов в точных науках:
• теория чисел (числа простые и периодические дроби), • геометрия (правильные многоугольники, теория поверхностей),
• алгебра (доказательство основной теоремы алгебры о числе корней алгебраического уравнения),
• астрономия (вычисление орбит планет),
• физика (электромагнетизм).
Труды К. Гаусса изданы в Германии в 12-ти томах.

Пример

А

B

C

D

I1

I2

I3

I4

I5

I6

6

3

3

3. от 1, 3, 4, и 6 строк отнимаем 2 строку, умноженную соответственно на 1; -1; -2; -3

Решим систему методом Гаусса

4. 3-ую строку делим на -1

6. 4-ую строку делим на -8

7. от 1, 3, 5 и 6 строк отнимаем 4 строку, умноженную соответственно на 1; 1; 4; 1

8. 5-ую строку делим на -5

10. 6-ую строку делим на -5,85

11. от 1, 2, 3, 4 и 5 строк отнимаем 6 строку, умноженную соответственно на 0,35; -1,3; -0,95; -0,05; -0,3

12. найдем приближенные значения

Ответ:

Решение СЛУ в Excel