Институт компьютерных систем и информационной безопасности
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электротехника. Резонанс в электрических цепях. (Лекция 9) презентация
Содержание
- 1. Электротехника. Резонанс в электрических цепях. (Лекция 9)
- 2. Учебные вопросы: 1. Резонанс напряжений. Параметры
- 3. Общие положения резонансных явлений в цепях переменного
- 4. 1. Резонанс напряжений. Параметры и частотные
- 5. Режим работы колебательного контура, содержащего последовательно соединенные
- 6. При резонансе ϕ = 0, если Х
- 7. Резонансные свойства (избирательность) контура характеризуются добротностью Пример:
- 8. Частотные характеристики последовательного контура Анализ характера уравнений
- 9. Рассмотрим частотные зависимости действующих значений тока в
- 10. На частотах ωL0 и ωС0 напряжения на
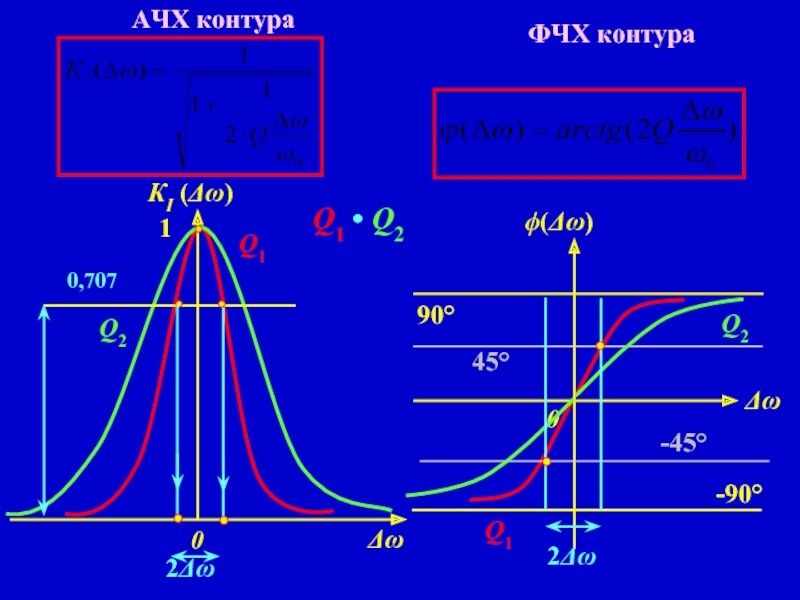
- 11. 0,707 АЧХ контура Q1 • Q2 Q1 Q1 Q2 Q2 ФЧХ контура
- 12. 2. Резонанс токов. Параметры и частотные
- 13. где резонансное сопротивление контура Аналитически АЧХ контура
- 14. Ток в неразветвленной части цепи R0 –
- 15. В реальном параллельном колебательном контуре резонансные избирательные
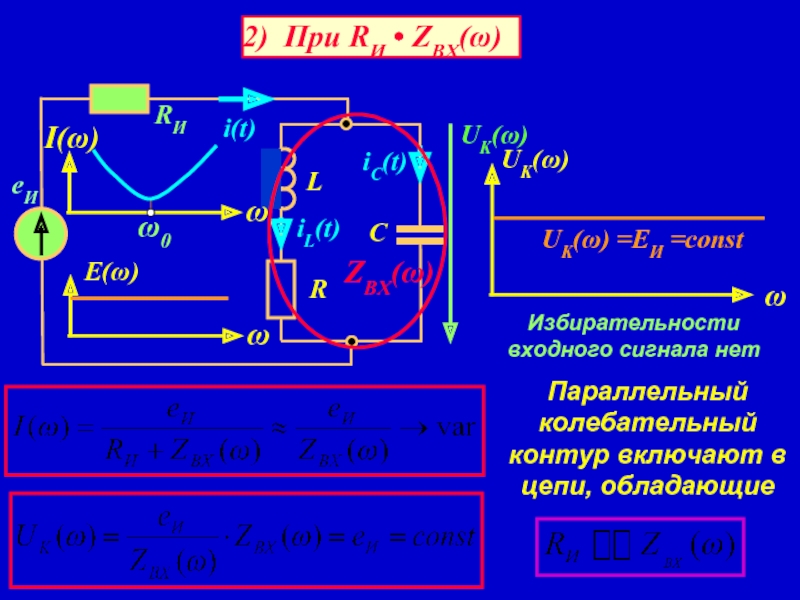
- 16. 2) При RИ • ZВХ(ω) UK(ω)
- 17. 3. Полоса пропускания колебательного контура Способность колебательного
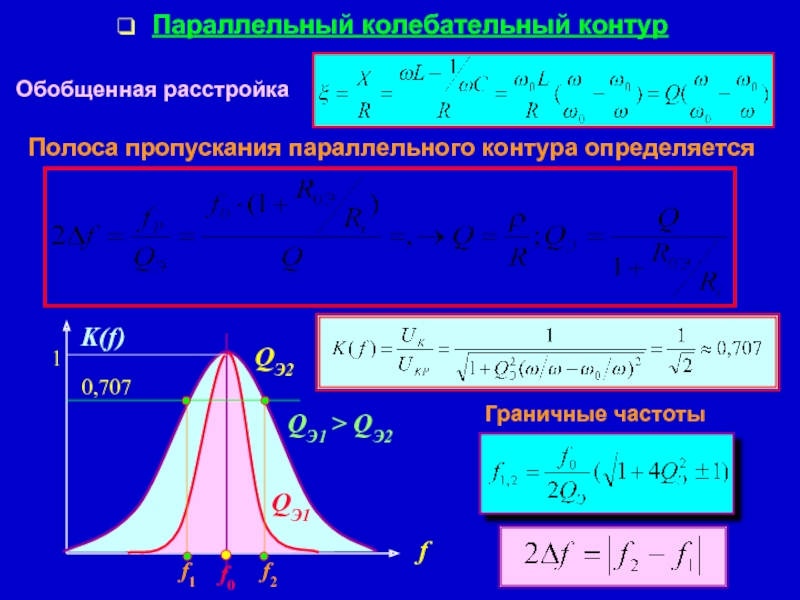
- 18. Параллельный колебательный контур Обобщенная расстройка
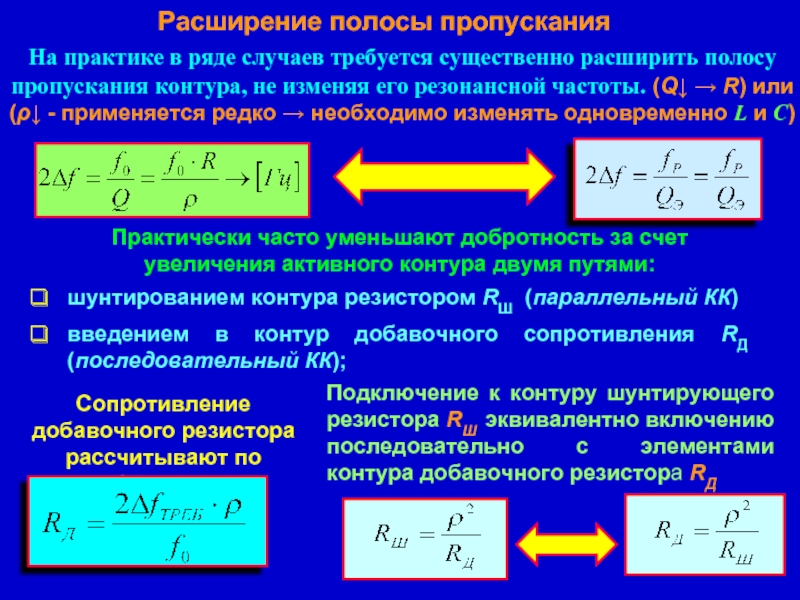
- 19. На практике в ряде случаев требуется существенно
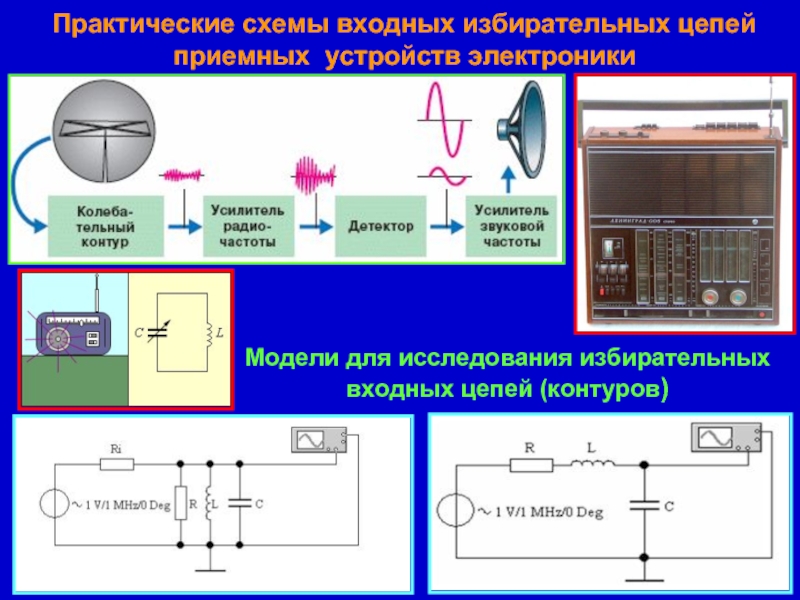
- 20. Практические схемы входных избирательных цепей приемных устройств электроники Модели для исследования избирательных входных цепей (контуров)
- 21. Однодиапазонный КВ приемник Входной контур приемника, может
- 22. Спектры входных сигналов радиостанций
- 23. Литература: Задание на самостоятельную работу 1. Нефедов
Слайд 1Учебная дисциплина
Электротехника
Лекция № 9
Резонанс в электрических цепях
Кубанский государственный технологический университет
Кафедра
Слайд 2Учебные вопросы:
1. Резонанс напряжений. Параметры и частотные характеристики колебательного контура.
2.
3. Полоса пропускания колебательного контура.
Литература:
1. Нефедов В.И.. Основы радиоэлектроники и связи: Учебник для вузов, - М.: Высшая школа, 2005 г, с. 219 – 226
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 54 – 66.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.: Высшая школа, 2003 г, с. 37 –83.
Слайд 3Общие положения резонансных явлений в цепях переменного тока
Амплитуды колебаний токов и
Резонанс является одним из самых распространенных в природе физических явлений.
Явление резонанса можно наблюдать в механических, электрических и даже тепловых системах.
Электрическая цепь в которой может возникнуть резонанс называется колебательным контуром
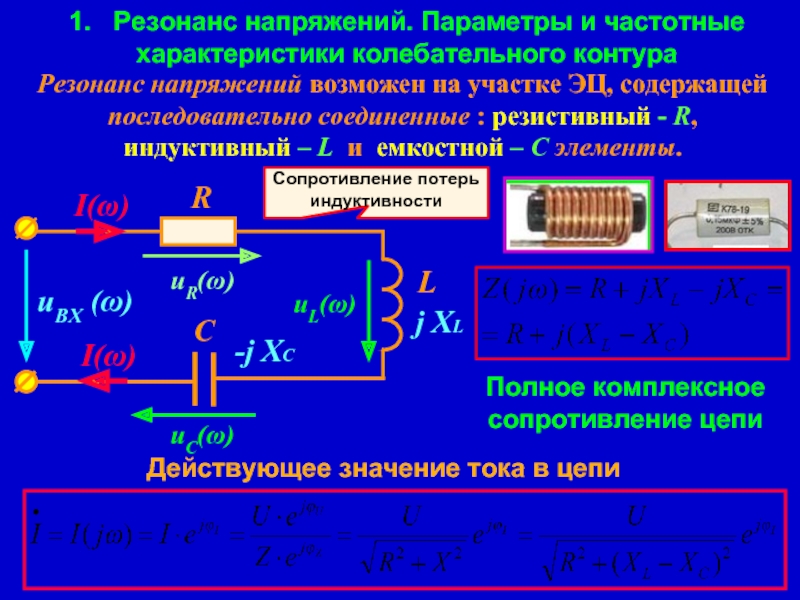
Слайд 41. Резонанс напряжений. Параметры и частотные характеристики колебательного контура
Резонанс напряжений
Действующее значение тока в цепи
Полное комплексное сопротивление цепи
Сопротивление потерь
индуктивности
Слайд 5Режим работы колебательного контура, содержащего последовательно соединенные резистивный - R, индуктивный
Аргумент Z характеризует сдвиг фаз между U и I
Модуль полного сопротивления цепи
Частота входного воздействия ω при которой реактивная составляющая входного сопротивления равна нулю называется резонансной частотой - ω0
Слайд 6При резонансе ϕ = 0, если Х = ХL – XC
Таким образом, в последовательном контуре из множества токов с различными частотами выделяется ток, только одной определенной частоты – ток резонансной частоты
Реактивные сопротивления контура на резонансной частоте ω0 равны друг другу.
Характеристическое (волновое) сопротивление контура
Слайд 7Резонансные свойства (избирательность) контура характеризуются добротностью
Пример: Пусть U= 12 В, XL(ω0)
Значение тока на резонансной частоте
Добротность показывает, во сколько раз резонансные напряжения на реактивных элементах превышают приложенное напряжение ⇒ отсюда и возник термин «резонанс напряжений»
Физический смысл добротности
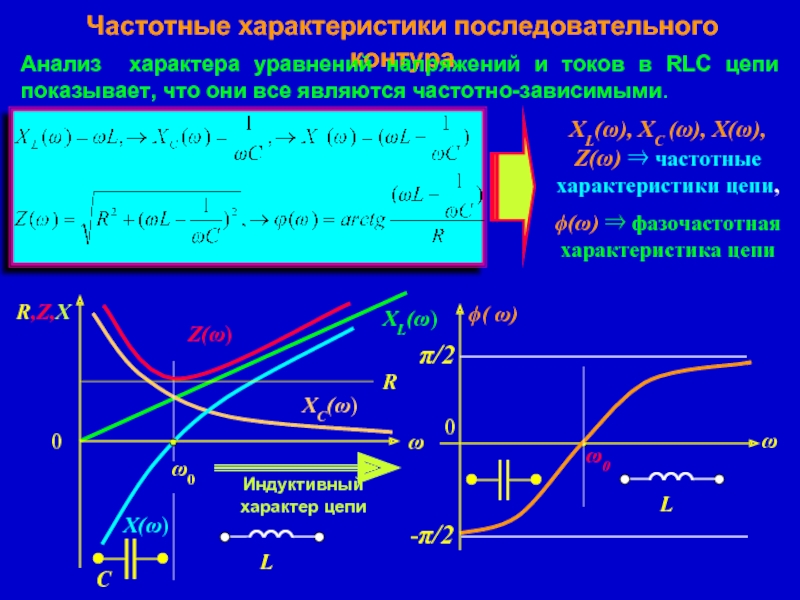
Слайд 8Частотные характеристики последовательного контура
Анализ характера уравнений напряжений и токов в RLC
XL(ω), XC (ω), X(ω), Z(ω) ⇒ частотные характеристики цепи,
ϕ(ω) ⇒ фазочастотная характеристика цепи
XL(ω)
ω0
С
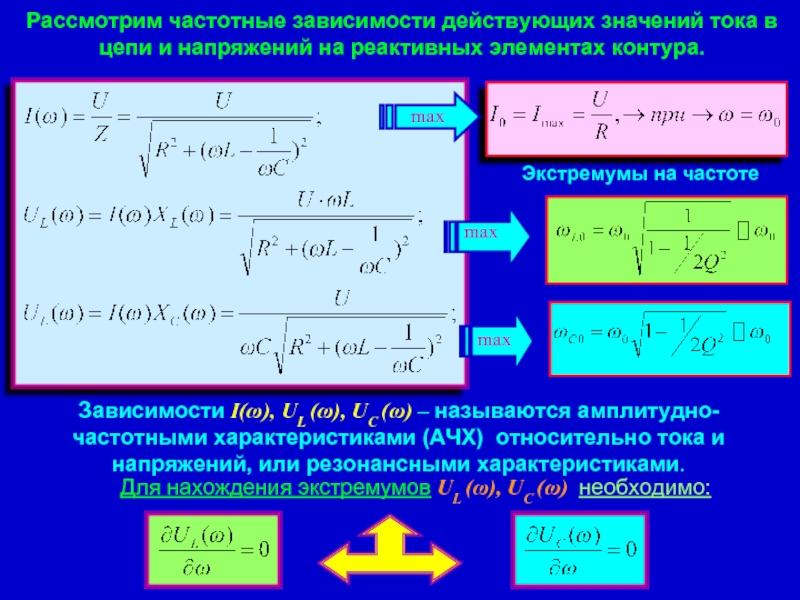
Слайд 9Рассмотрим частотные зависимости действующих значений тока в цепи и напряжений на
Зависимости I(ω), UL (ω), UC (ω) – называются амплитудно-частотными характеристиками (АЧХ) относительно тока и напряжений, или резонансными характеристиками.
Экстремумы на частоте
Для нахождения экстремумов UL (ω), UC (ω) необходимо:
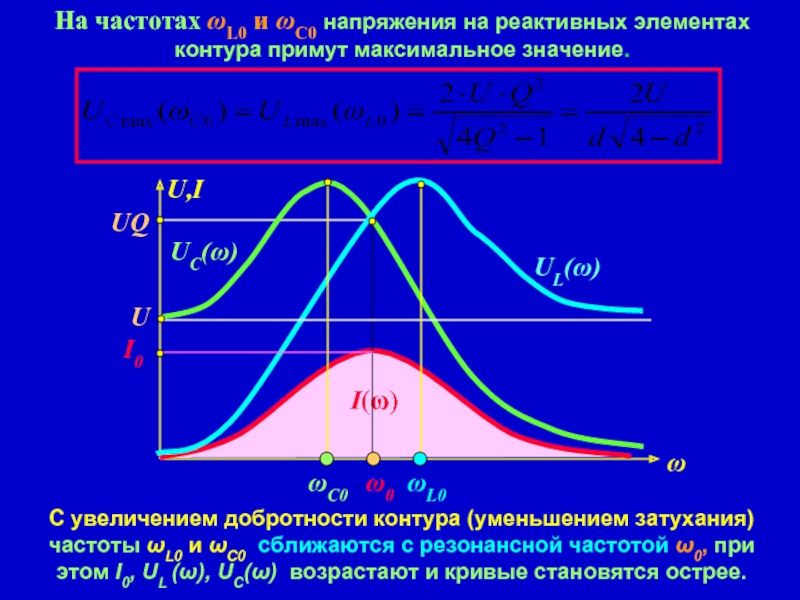
Слайд 10На частотах ωL0 и ωС0 напряжения на реактивных элементах контура примут
С увеличением добротности контура (уменьшением затухания) частоты ωL0 и ωС0 сближаются с резонансной частотой ω0, при этом I0, UL (ω), UC(ω) возрастают и кривые становятся острее.
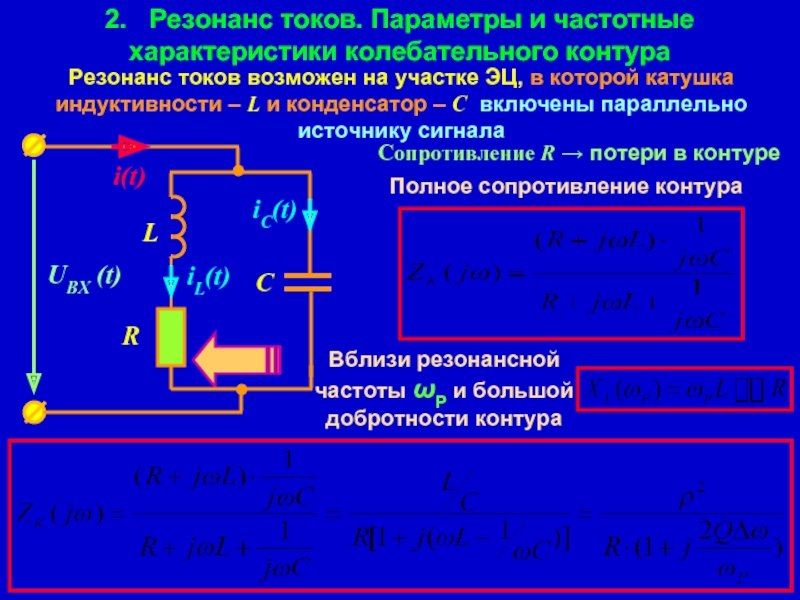
Слайд 122. Резонанс токов. Параметры и частотные характеристики колебательного контура
Резонанс токов
Сопротивление R → потери в контуре
Полное сопротивление контура
Вблизи резонансной частоты ωР и большой добротности контура
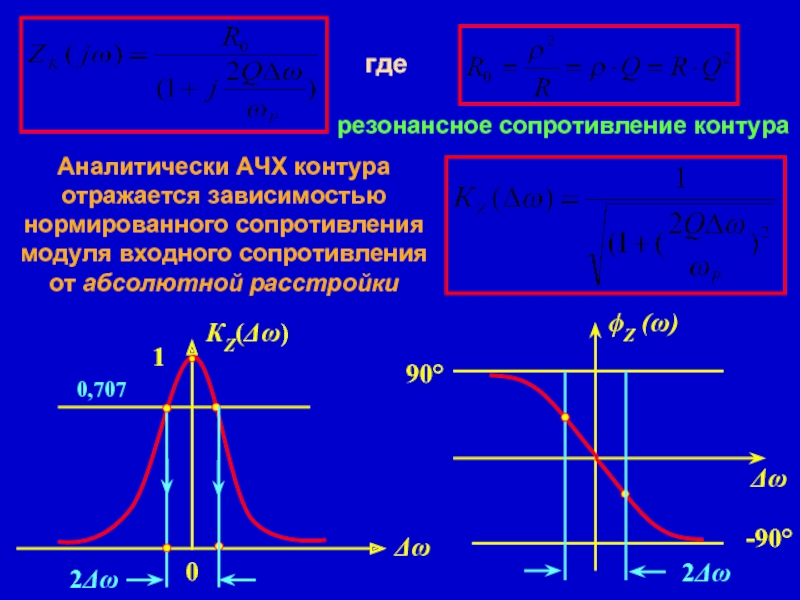
Слайд 13где
резонансное сопротивление контура
Аналитически АЧХ контура отражается зависимостью нормированного сопротивления модуля входного
0,707
Слайд 14Ток в неразветвленной части цепи
R0 – эквивалентное резонансное сопротивление контура
Режим работы
Токи в параллельных ветвях цепи при резонансе
Ток в индуктивной ветви
Ток в емкостной ветви
Отсюда возник термин «резонанс токов»
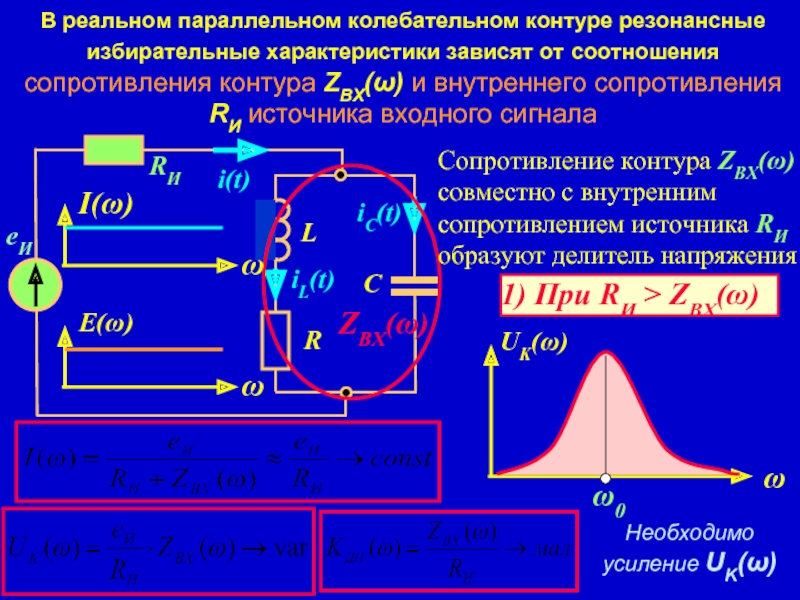
Слайд 15В реальном параллельном колебательном контуре резонансные избирательные характеристики зависят от соотношения
Сопротивление контура ZВХ(ω) совместно с внутренним сопротивлением источника RИ образуют делитель напряжения
1) При RИ > ZВХ(ω)
ω0
Необходимо усиление UK(ω)
Слайд 162) При RИ • ZВХ(ω)
UK(ω) =EИ =const
Избирательности входного сигнала нет
Параллельный колебательный
Слайд 173. Полоса пропускания колебательного контура
Способность колебательного контура выделять сигналы заданной частоты
Контур с лучшей избирательностью обладает большей добротностью
Избирательность характеризуется формой амплитудно-частотной характеристики (АЧХ) контура
Полосой пропускания называется область частот, вблизи резонансной частоты, в пределах которой н модуль коэффициента передачи уменьшается в заданное число раз (чаше всего в √2 раз).
Последовательный колебательный контур
Нормированная АЧХ (UВЫХ = UC)
0,707
1
Q1> Q2> Q3
Полоса пропускания
Слайд 18 Параллельный колебательный контур
Обобщенная расстройка
Полоса пропускания параллельного контура определяется
QЭ1 >
Граничные частоты
Слайд 19На практике в ряде случаев требуется существенно расширить полосу пропускания контура,
шунтированием контура резистором RШ (параллельный КК)
Сопротивление добавочного резистора рассчитывают по формуле
Подключение к контуру шунтирующего резистора RШ эквивалентно включению последовательно с элементами контура добавочного резистора RД
Практически часто уменьшают добротность за счет увеличения активного контура двумя путями:
введением в контур добавочного сопротивления RД (последовательный КК);
Расширение полосы пропускания
Слайд 20Практические схемы входных избирательных цепей приемных устройств электроники
Модели для исследования избирательных
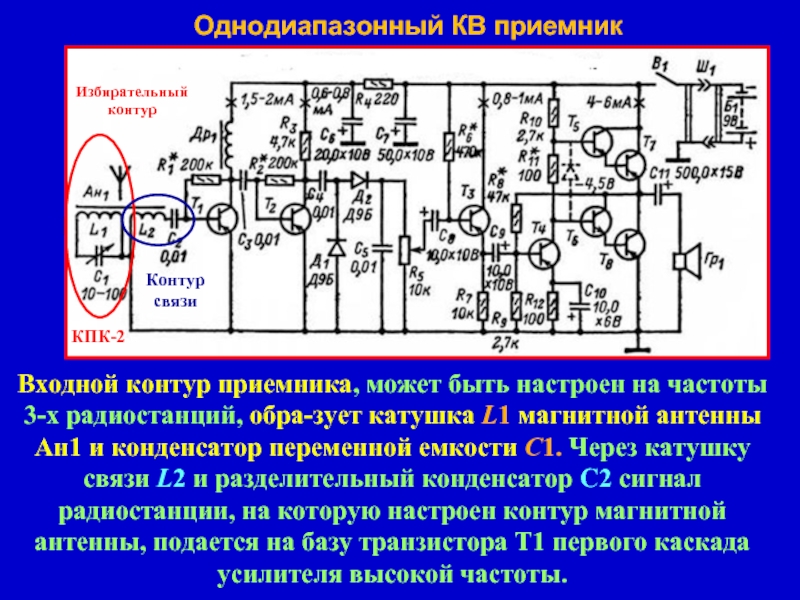
Слайд 21Однодиапазонный КВ приемник
Входной контур приемника, может быть настроен на частоты 3-х
Контур связи
КПК-2
Избирательный контур
Слайд 22
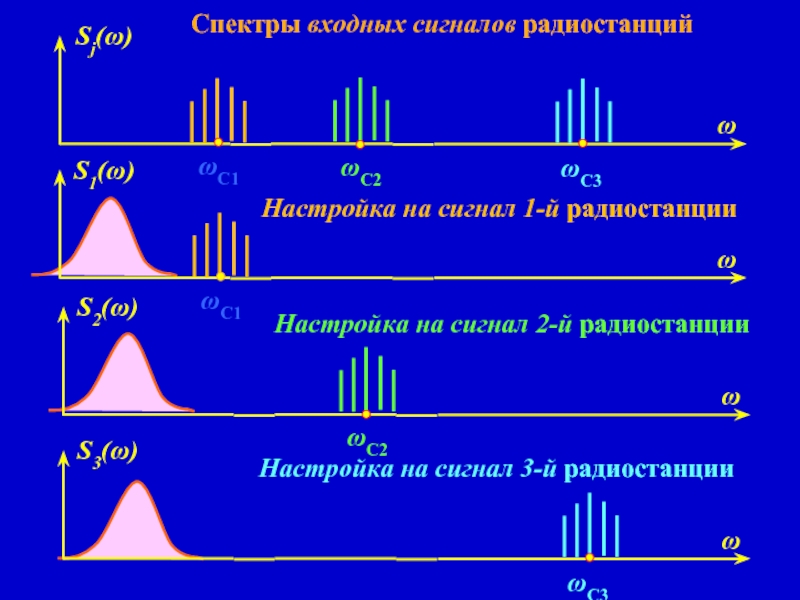
Спектры входных сигналов радиостанций
Настройка на сигнал 1-й радиостанции
Настройка на сигнал 2-й
Настройка на сигнал 3-й радиостанции
Слайд 23Литература:
Задание на самостоятельную работу
1. Нефедов В.И.. Основы радиоэлектроники и связи: Учебник
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 54 – 66.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.: Высшая школа, 2003 г, с. 37 –83.