- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электростатическое поле в диэлектрике. Лекция 3 презентация
Содержание
- 1. Электростатическое поле в диэлектрике. Лекция 3
- 2. Электрический диполь в э/ст поле Электрический
- 3. Потенциал поля диполя Так как r>>l (диполь точечный), то и (3.2)
- 7. Поле диполя обладает осевой симметрией.
- 8. Диполь в однородном электрическом поле
- 9. M = 0, если α = 0
- 10. Диполь в неоднородном электрическом поле С учетом малых размеров диполя
- 11. Проекция результирующей силы, действующей на диполь в
- 12. Потенциальная энергия диполя, помещенного в однородное электрическое поле
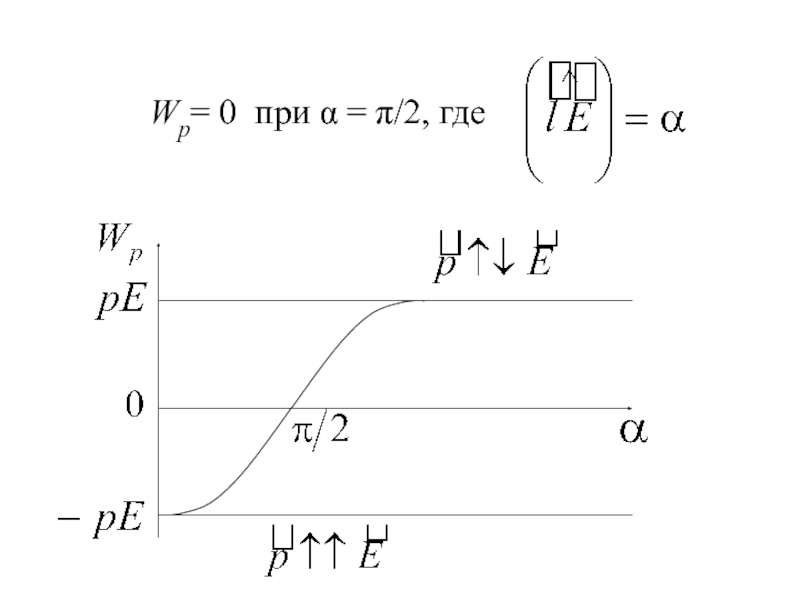
- 13. Wp= 0 при α = π/2, где
- 15. Выделим малый объем диэлектрика в виде наклонной
- 16. При неоднородной поляризации диэлектрика связанные заряды появляются
- 17. Вектор электрического смещения В СИ
- 18. Обобщение теоремы Гаусса где q и
- 19. Поток В дифференциальной форме или
- 20. Поле на границе раздела диэлектриков Выделим
- 21. Пусть h→0 а ΔS достаточно мало. Из теоремы Гаусса: Учитывая, что (3.19) (3.20)
- 22. Рассматривая диэлектрик с из (3.20)
- 23. или (3.22) тогда (3.23) При
- 24. Из рисунка С учетом (3.20) и (3.23): и получим (3.24)
Слайд 2Электрический диполь в э/ст поле
Электрический диполь – система двух разноименных
Электрический дипольный момент
(3.1)
Слайд 9 M = 0, если α = 0 или α = π
(3.4)
Под действием момента сил
диполь будет стремиться установиться по полю
С учетом направлений
Слайд 11 Проекция результирующей силы, действующей на диполь в направлении оси x
При 0
Слайд 15 Выделим малый объем диэлектрика в виде наклонной призмы. Ее дипольный момент
(3.8)
(3.9)
Приравниваем (3.8) и (3.9)
(3.10)
Слайд 16При неоднородной поляризации диэлектрика связанные заряды появляются не только на поверхности
(3.11)
Связанный поляризационный заряд
Тогда теорема Гаусса в интегральной форме
(3.12)
Отрицательные связанные заряды являются источником линий
Слайд 17Вектор электрического смещения
В СИ
В изотропных диэлектриках
Тогда
В случае
и
могут быть неколлинеарными.
(3.13)
(3.14)
(3.15)
[Кл/м2 ]
Слайд 18Обобщение теоремы Гаусса
где q и q′ – сторонние и связанные
Тогда
(3.17)
Теорема Гаусса для вектора электрического смещения в интегральной форме
(3.16)
Слайд 19 Поток
В дифференциальной форме
или
В диэлектриках обычно связанные заряды не заданы и
(3.18)
через замкнутую поверхность равен алгебраической сумме сторонних зарядов, заключенных внутри этой поверхности.
Слайд 20Поле на границе раздела диэлектриков
Выделим малый участок границы раздела 2-х
– электрические смещения полей в 2-х диэлектриках вблизи границы раздела.
Слайд 22Рассматривая диэлектрик с
из (3.20)
(3.21)
Выделим прямоугольный замкнутый контур; l достаточно мало, а
Из теоремы о циркуляции:




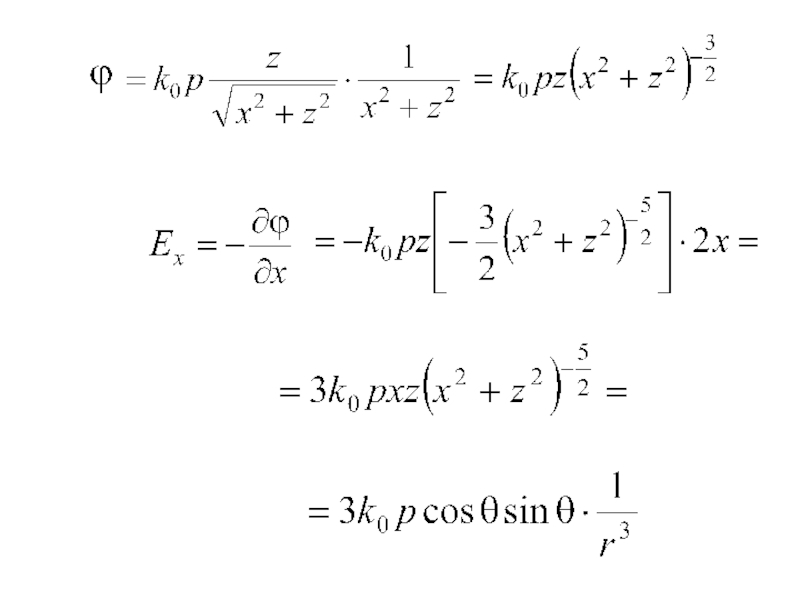
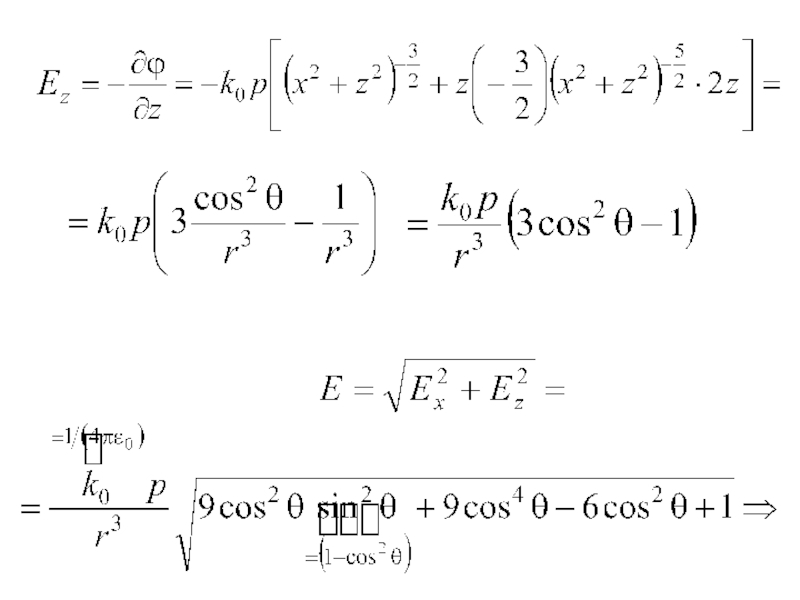









![Вектор электрического смещения В СИ В изотропных диэлектриках Тогда В случае анизотропных диэлектриковимогут быть неколлинеарными.(3.13)(3.14)(3.15)[Кл/м2 ]](/img/tmb/5/475732/9a19b900512e4fb6b480aa63dcefc812-800x.jpg)