- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Електропровідність халькогенідних склоподібних напівпровідників. (Лекція 6) презентация
Содержание
- 1. Електропровідність халькогенідних склоподібних напівпровідників. (Лекція 6)
- 2. Анізотропія електропровідності шаруватих кристалів Анізотропія
- 3. Рис. 2. Модель перенесення носіїв заряду поперек
- 4. По аналогії з аморфними напівпровідниками, феноменологічний опис
- 5. Рис. 6. Діаграма густини станів для аморфних
- 6. Температурна залежність електропровідності на постійному струмі
- 7. де Со =
- 8. Стрибковий механізм провідності Якщо теплової енергії носія
- 9. Якщо густина станів на рівні Фермі ЕF
- 10. де
- 11. Загальний вигляд залежності провідності у координатах lnσ
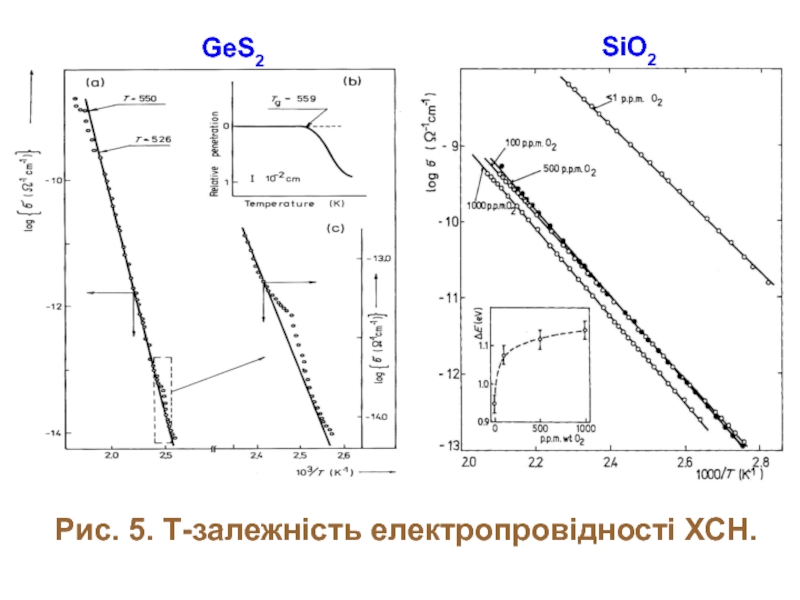
- 12. Рис. 5. Т-залежність електропровідності ХСН. GeS2 SiO2
- 13. Вплив домішок на електропровідність ХСН Рис. 7.
- 14. Вплив домішок на електропровідність ХСН Рис. 8.
- 15. Електропровідність суперіонних ХСН Таблиця. Основні параметри іонної
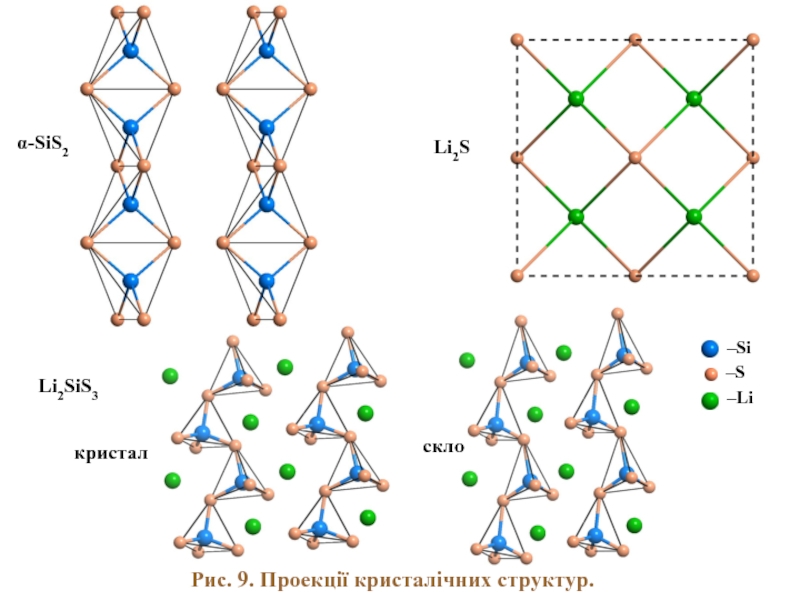
- 16. Li2S Li2SiS3 кристал скло Рис. 9. Проекції кристалічних структур. α-SiS2
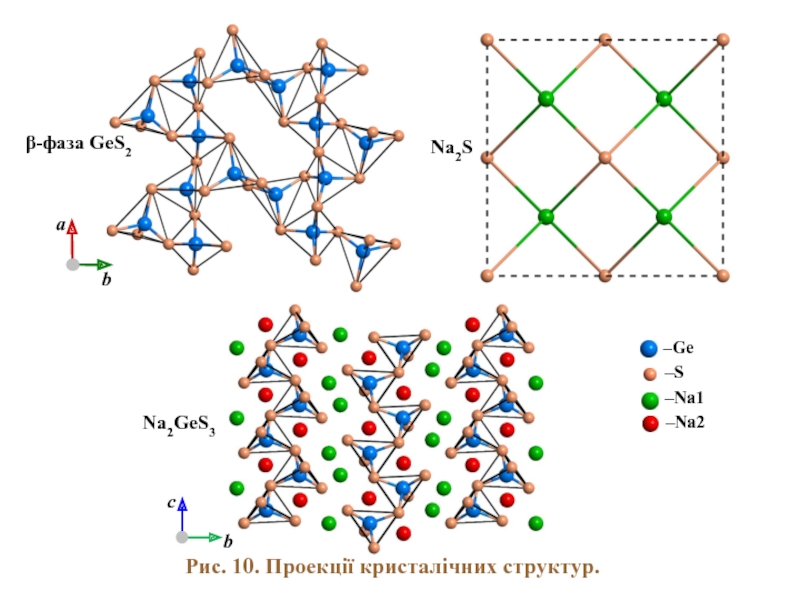
- 17. Рис. 10. Проекції кристалічних структур. Na2S Na2GeS3 –Na1 β-фаза GeS2 –Ge –S –Na2
- 18. в) г) д) Рис. 11. Розподіл валентної
- 19. Рис. 12. Температурні залежності провідності кристалічних фаз
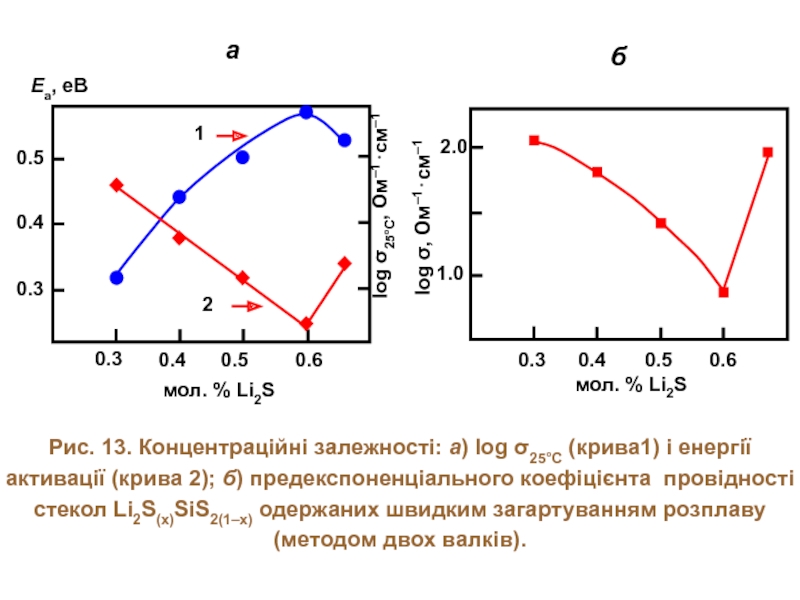
- 20. Рис. 13. Концентраційні залежності: а) log σ25°C
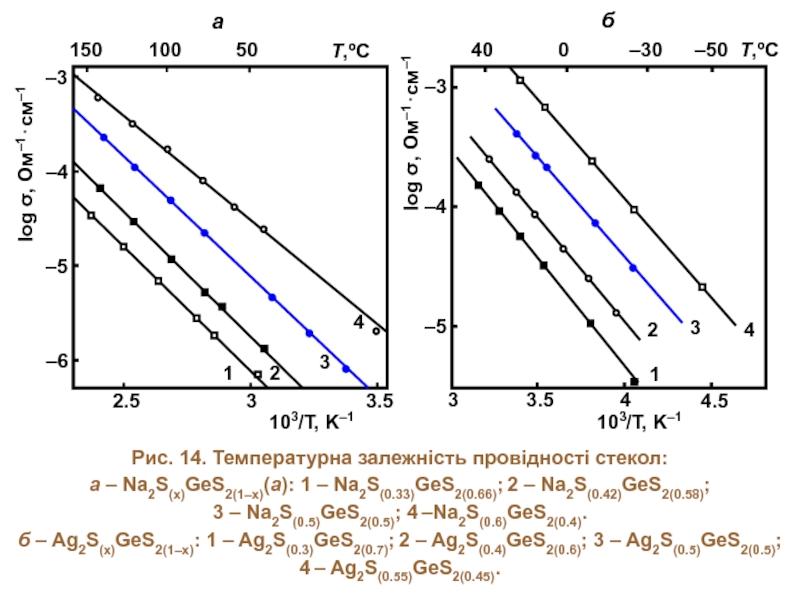
- 21. Рис. 14. Температурна залежність провідності стекол: а
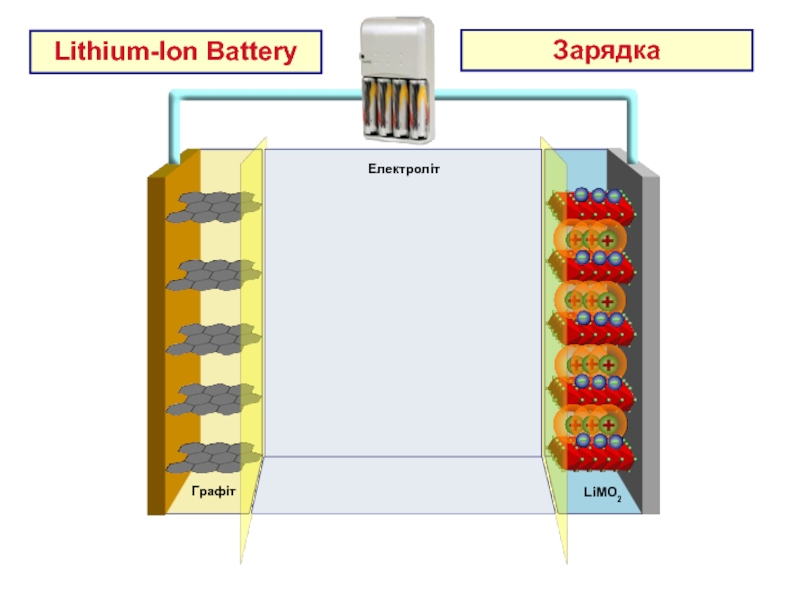
- 22. AL Current Collector Cu Current Collector Електроліт LiMO2 Графіт Lithium-Ion Battery Зарядка
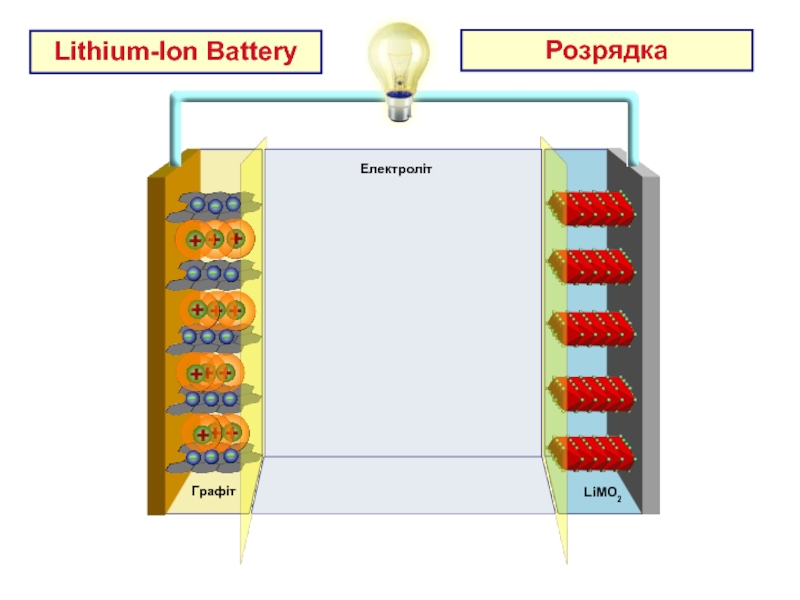
- 23. AL Current Collector Cu Current Collector Електроліт LiMO2 Графіт Lithium-Ion Battery Розрядка
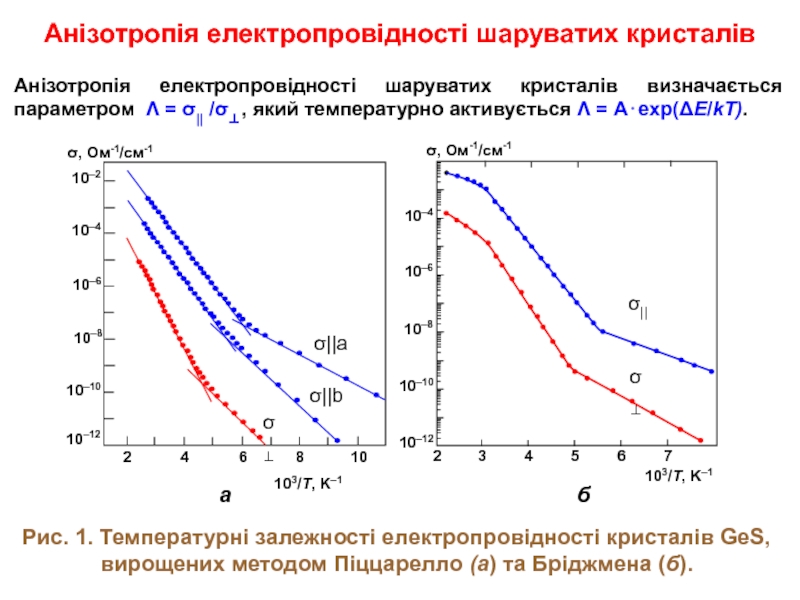
Слайд 2Анізотропія електропровідності шаруватих кристалів
Анізотропія електропровідності шаруватих кристалів визначається параметром Λ
Рис. 1. Температурні залежності електропровідності кристалів GeS, вирощених методом Піццарелло (а) та Бріджмена (б).
σ, Ом-1/см-1
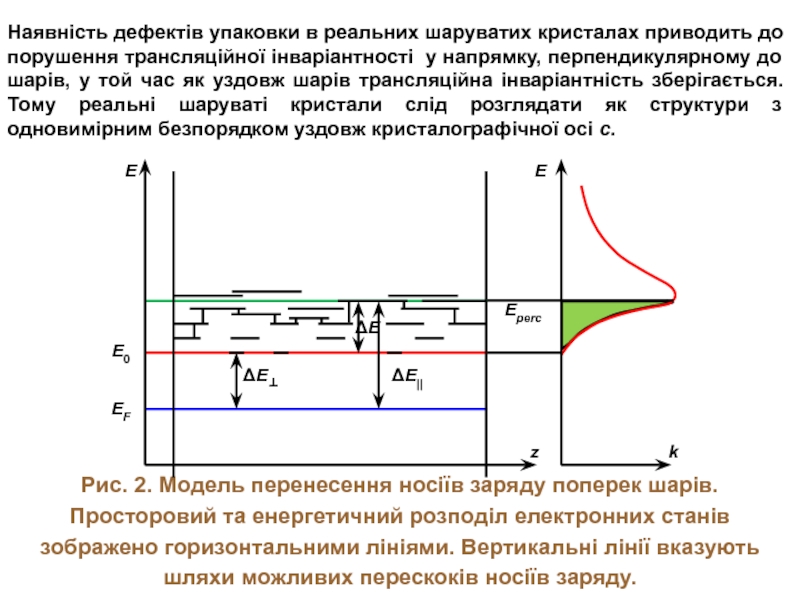
Слайд 3Рис. 2. Модель перенесення носіїв заряду поперек шарів. Просторовий та енергетичний
EF
E0
ΔE||
ΔE⊥
ΔE
E
E
Eperc
z
k
Наявність дефектів упаковки в реальних шаруватих кристалах приводить до порушення трансляційної інваріантності у напрямку, перпендикулярному до шарів, у той час як уздовж шарів трансляційна інваріантність зберігається. Тому реальні шаруваті кристали слід розглядати як структури з одновимірним безпорядком уздовж кристалографічної осі с.
Слайд 4По аналогії з аморфними напівпровідниками, феноменологічний опис властивостей переносу в шаруватих
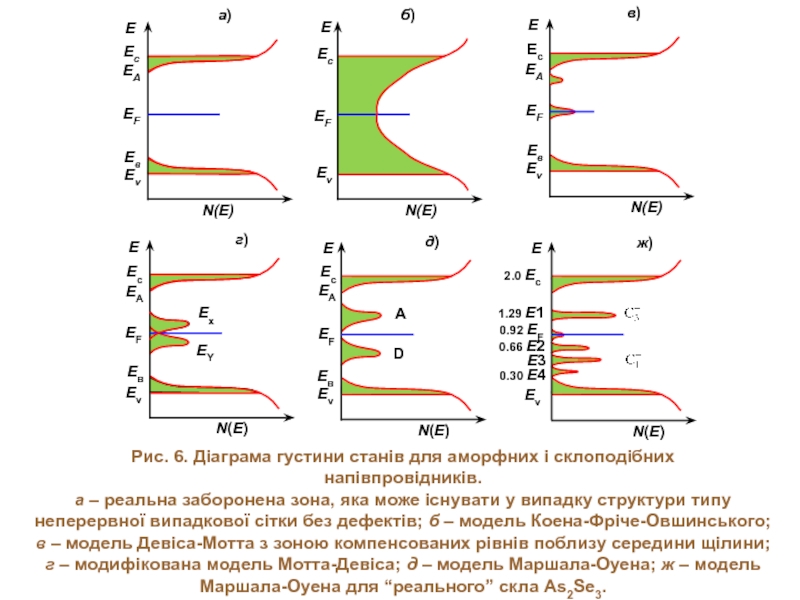
Слайд 5Рис. 6. Діаграма густини станів для аморфних і склоподібних
напівпровідників.
а – реальна
Слайд 6Температурна залежність електропровідності на постійному струмі
Халькогенідні стекла є напівпровідниками, однією з
Ec
EA
EF
EB
Ev
N
Еσ
3
1
2
Рис. 3. Схема густини станів в ХСН і можливих трьох механізмів
перенесення заряду. 1 – збудження в зонні стани; 2 – збудження в
локалізовані стани в області Елок; 3 – стрибки електронів поблизу
енергії Фермі.
а
б
Слайд 7де Со =
У випадку електронної провідності Еа являє собою різницю енергій нижнього краю зони провідності Ес і рівня Фермі ЕF, При наяв-ності діркової провідності відповідно де Еv – енергія верхньої границі валентної зони.
1. Переніс носіїв між делокалізованими станами у зоні провідності (Е > Ес) і у валентній зоні (Е < Еv); наявність таких станів обумовлено ближнім порядком. У цьому випадку носії термічним і оптичним шляхом збуджуються за край рухливості у нелокалізовані стани, тобто стани, розповсюджені по всьому об’єму тіла, з енергіями Ес і Еv (рис. 3, а). У цьому випадку електропровідність, яка відповідає переносу носіїв за краями рухливостей, описується рівнянням:
Якщо (Ес – ЕF) є лінійною функцією Т в усьому досліджуваному інтервалі температур, то графік залежностей lnσ від 1/Т є пряма лінія. У цьому випадку можна записати:
де Е(0) – величина (Ес – ЕF) при Т = 0 К, а γ − її температурний коефіцієнт.
Підставляючи (2) у (1), одержимо вираз для провідності по розпростертим станам:
(1)
(2)
(3)
Слайд 8Стрибковий механізм провідності
Якщо теплової енергії носія заряду недостатньо, щоб піднятися із
Провідність, зв’язана з носіями, які збуджуються у локалізовані стани на краях зон, тобто поблизу ЕА і ЕВ (рис. 3), здійснюється шляхом стрибків і описується виразом:
де W1 – енергія активації стрибків, яка повинна зменшуватися зі зменшенням температури, оскільки по своїй природі провідність має перескоковий характер зі змінною довжиною стрибка. Провідність по локалізованим станам у хвостах дозволених зон характеризуються активаційною залежністю рухливості:
де ΔЕ – різниця енергій рівнів, між якими здійснюється перехід.
(4)
(5)
Слайд 9Якщо густина станів на рівні Фермі ЕF скінчена, то провідність одержує
і виразу D = 1/6 p a2) рівняння типу:
де N(EF) – густина дефектних станів поблизу рівня Фермі, а N(EF)kT – число електронів, які приймають участь у провідності. W2 – енергія активації стрибка, величина якого порядку половини ширини зони локалізованих станів при умові, що густина станів N(E) має вигляд, наведений на рис. 3. Відмітимо, що залежність lnσ від 1/Т буде мати вигляд прямої тільки якщо стрибки відбуваються між найближчими сусідами.
(6)
Слайд 10де
При ще більш низьких температурах носії старатимуться стрибнути за межі своїх просторово самих близьких сусідніх станів у стани з мінімально можливою різницею енергії. Таким чином, при дуже низьких температурах можна очікувати, що відбувається провідність зі змінною довжиною стрибка по локалізованим станам поблизу рівня Фермі. При такому механізмі переносу заряду справджується закон Мотта:
Врахування усіх трьох механізмів переносу дає наступний вираз для електропровідності склоподібних напівпровідників:
(7)
(8)
(9)
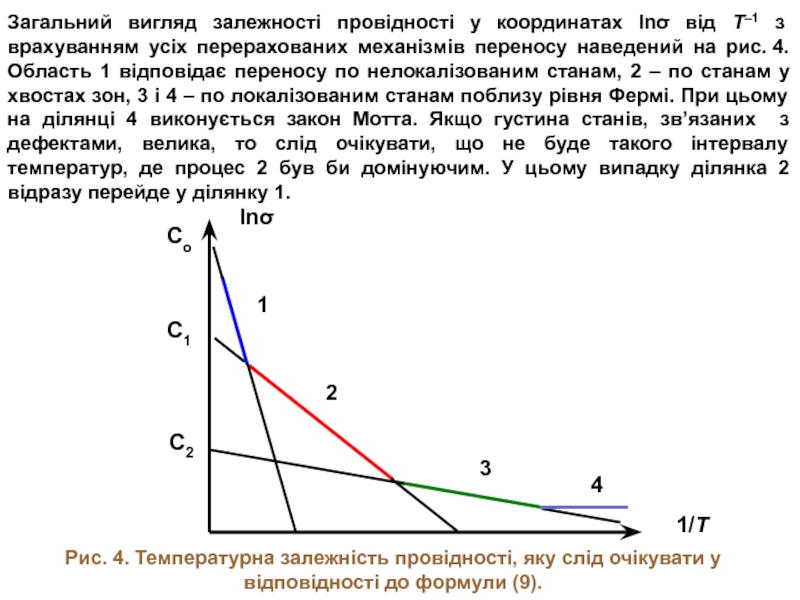
Слайд 11Загальний вигляд залежності провідності у координатах lnσ від Т–1 з врахуванням
Рис. 4. Температурна залежність провідності, яку слід очікувати у
відповідності до формули (9).
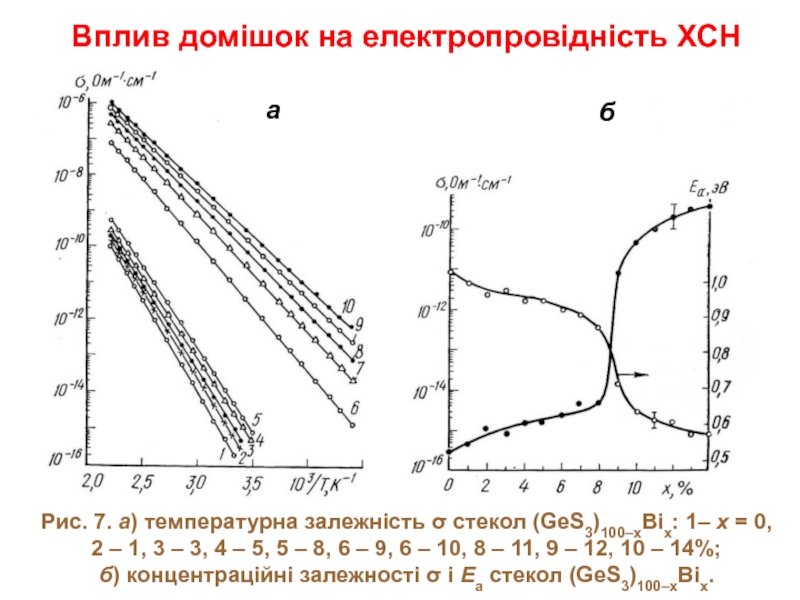
Слайд 13Вплив домішок на електропровідність ХСН
Рис. 7. а) температурна залежність σ стекол
б) концентраційні залежності σ і Еа стекол (GeS3)100–xBix.
а
б
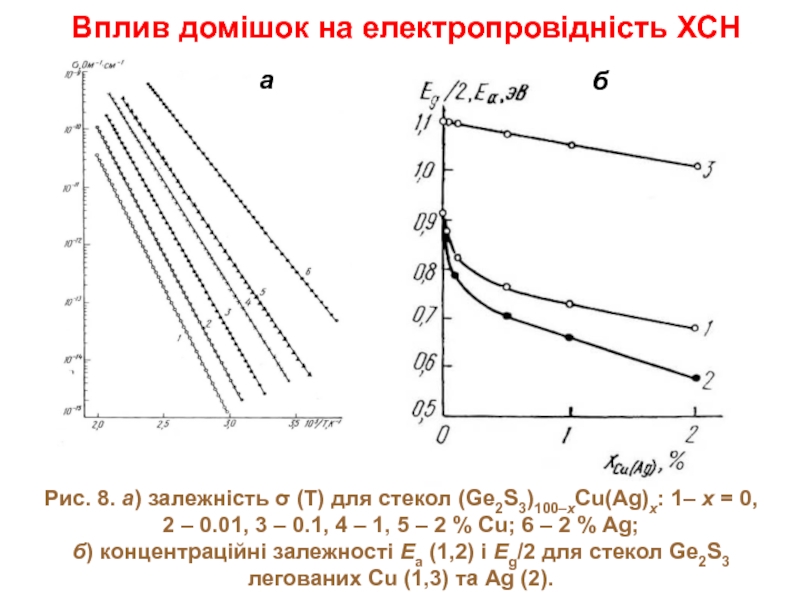
Слайд 14Вплив домішок на електропровідність ХСН
Рис. 8. а) залежність σ (Т) для
б) концентраційні залежності Еа (1,2) і Eg/2 для стекол Ge2S3 легованих Cu (1,3) та Ag (2).
а
б
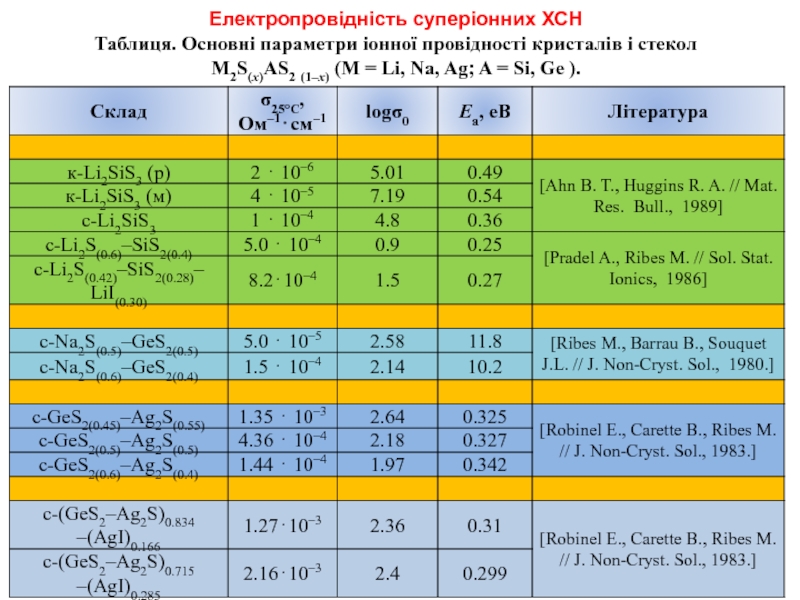
Слайд 15Електропровідність суперіонних ХСН
Таблиця. Основні параметри іонної провідності кристалів і стекол
M2S(x)AS2
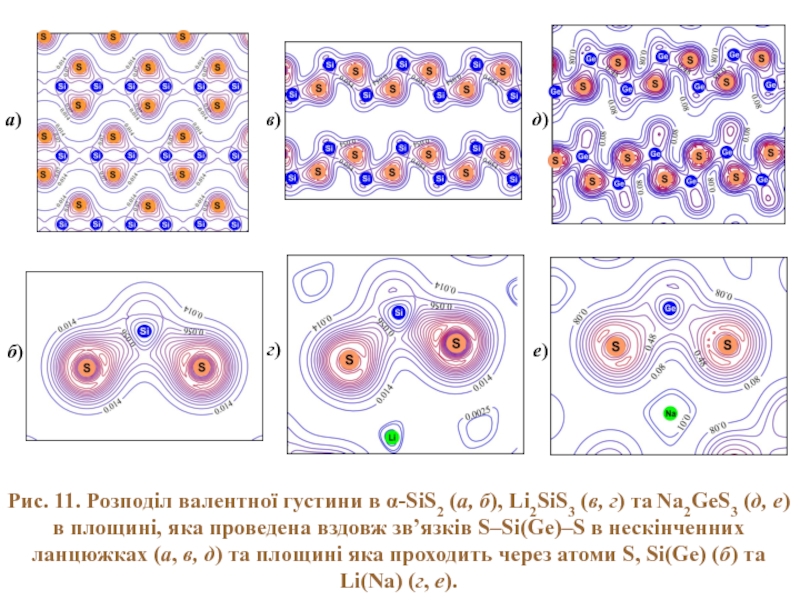
Слайд 18в)
г)
д)
Рис. 11. Розподіл валентної густини в α-SiS2 (а, б), Li2SiS3 (в,
е)
а)
б)
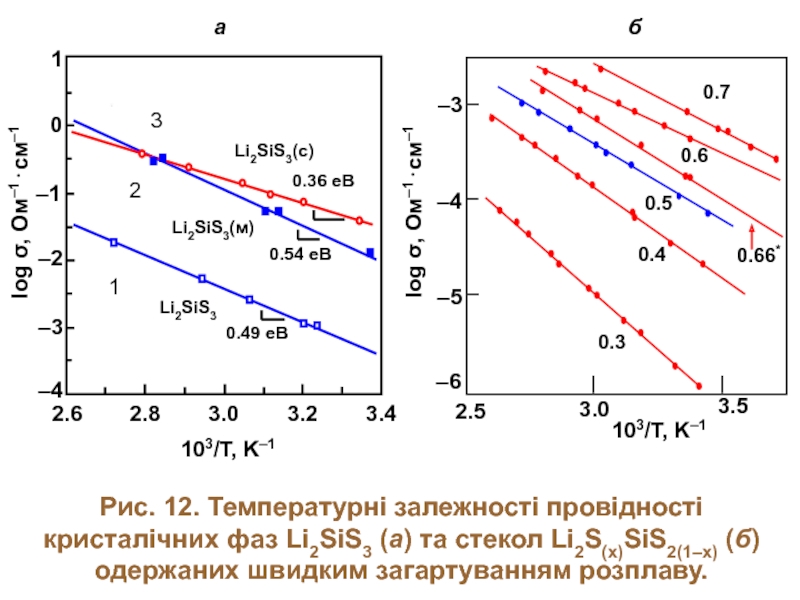
Слайд 19Рис. 12. Температурні залежності провідності кристалічних фаз Li2SiS3 (а) та стекол
б
а
Слайд 20Рис. 13. Концентраційні залежності: а) log σ25°C (крива1) і енергії активації
а
б
Слайд 21Рис. 14. Температурна залежність провідності стекол:
а – Na2S(x)GeS2(1–x)(а): 1 – Na2S(0.33)GeS2(0.66);
б – Ag2S(x)GeS2(1–x): 1 – Ag2S(0.3)GeS2(0.7); 2 – Ag2S(0.4)GeS2(0.6); 3 – Ag2S(0.5)GeS2(0.5); 4 – Ag2S(0.55)GeS2(0.45).
103/T, K–1
3
3.5
4
4.5
–5
–4
–3
log σ, Ом–1⋅cм–1
40
0
–30
–50
T,ºC
1
2
3
4
а
б