- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электромагнитные волны презентация
Содержание
- 1. Электромагнитные волны
- 2. ЛИТЕРАТУРА: Иродов И.Е. Основные законы. Волновые процессы;
- 3. Уравнения Максвелла Электростатика Электродинамика – закон Кулона
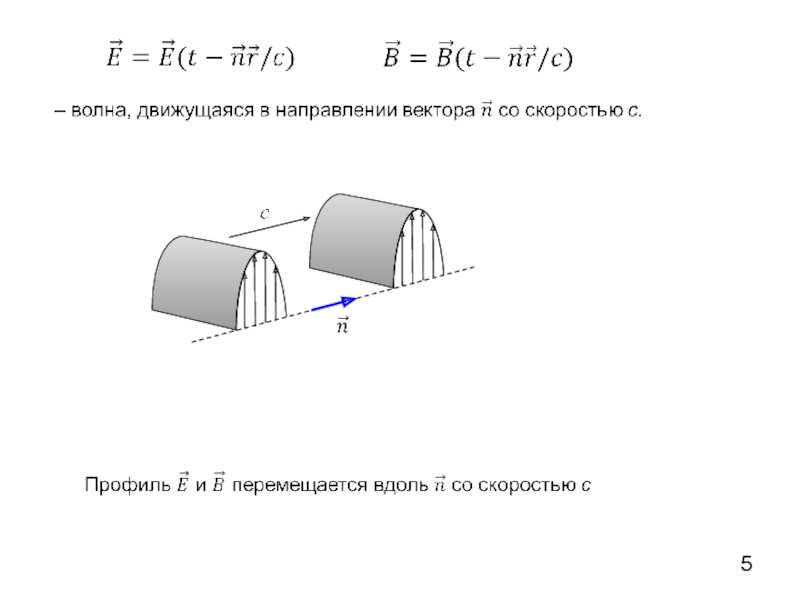
- 4. Частное решение –
- 5.
- 6. Существование электромагнитных волн было предсказано Фарадеем, а
- 7. Гармоническая (монохроматическая) волна с
- 8. Свойства гармонических волн
- 9. Поток энергии – объемная плотность
- 10. Электромагнитные волны в диэлектриках –
- 11. Среда ε = const, μ = const,
- 12. Давление и импульс электромагнитных волн Внутри проводника
- 13. электромагнитная волна обладает импульсом
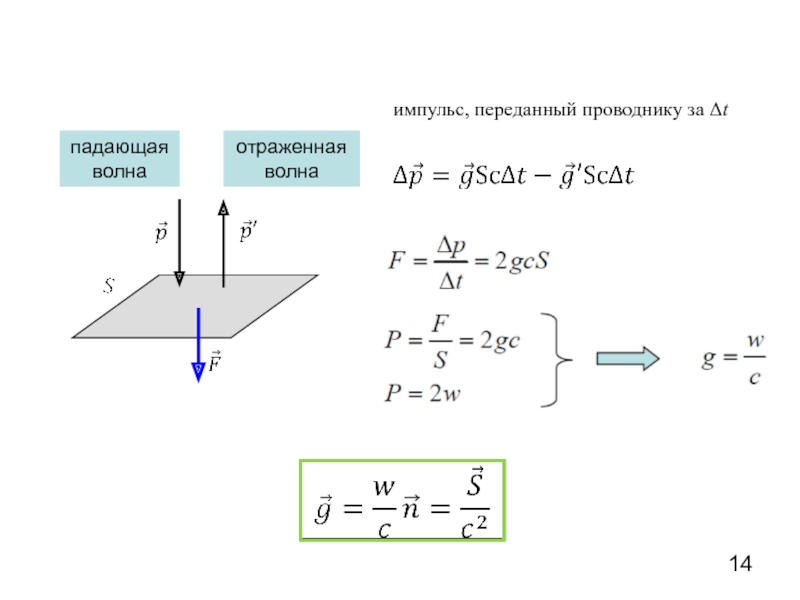
- 14. импульс, переданный проводнику за Δt падающая волна отраженная волна
- 15. Излучение электромагнитных волн. Вибратор Герца –
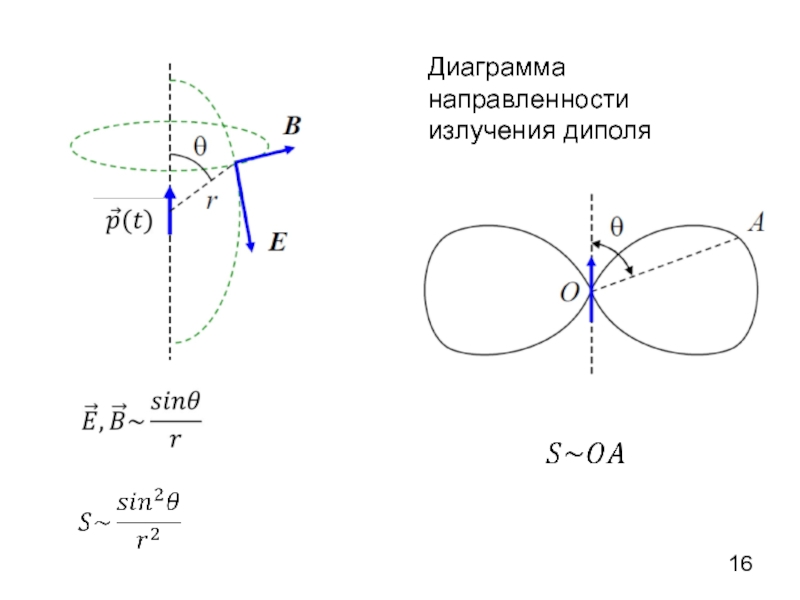
- 16. Диаграмма направленности излучения диполя
ЛИТЕРАТУРА: Иродов И.Е. Основные законы. Волновые процессы; Основные законы. Квантовая физика Орир Дж. Физика. Полный курс. Джанколи Д. Физика. Том 2. Матвеев А.Н. Курс общей физики. Том 4,5. Савельев И.А. Курс
Слайд 2ЛИТЕРАТУРА:
Иродов И.Е. Основные законы. Волновые процессы; Основные законы. Квантовая физика
Орир Дж.
Физика. Полный курс.
Джанколи Д. Физика. Том 2.
Матвеев А.Н. Курс общей физики. Том 4,5.
Савельев И.А. Курс общей физики. Том 3.
Трофимова Т.И. Курс физики.
Сивухин Д.В. Общий курс физики. Том 4, 5.
Джанколи Д. Физика. Том 2.
Матвеев А.Н. Курс общей физики. Том 4,5.
Савельев И.А. Курс общей физики. Том 3.
Трофимова Т.И. Курс физики.
Сивухин Д.В. Общий курс физики. Том 4, 5.
Слайд 3Уравнения Максвелла
Электростатика
Электродинамика
– закон Кулона
– сила Лоренца
– уравнения Максвелла
(в вакууме)
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Слайд 4
Частное решение – плоские бегущие волны
Одномерное волновое уравнение:
волновое уравнение
- волновое
уравнение плоской электромагнитной волны, распространяющейся вдоль оси X
Слайд 6Существование электромагнитных волн было предсказано Фарадеем, а затем Максвелл обосновал их
существование. Герц экспериментально подтвердил справедливость теории Максвелла.
Если возбудить с помощью колеблющейся системы переменное электромагнитное поле, то в окружающем пространстве возникнет последовательность взаимно превращающихся друг в друга переменных электрических и магнитных полей, распространяющихся от точки к точке в виде электромагнитных волн.
51
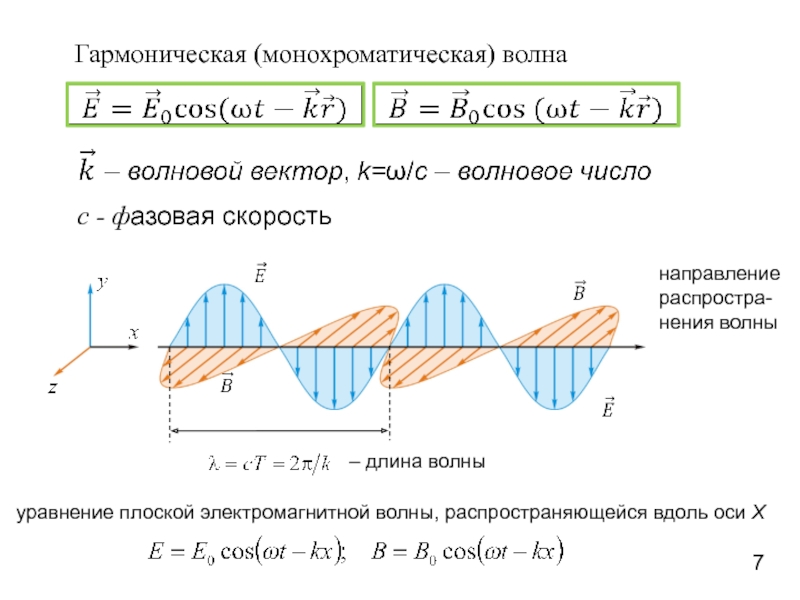
Слайд 7Гармоническая (монохроматическая) волна
с - фазовая скорость
уравнение плоской электромагнитной волны, распространяющейся вдоль
оси X
– длина волны
направление распростра-нения волны
Слайд 9Поток энергии
– объемная плотность электромагнитной энергии
скорость переноса энергии плоской гармонической волной
в вакууме равна скорости света
вектор Пойнтинга (вектор Умова — Пойнтинга)
Плотность потока энергии - энергия, переносимая волной в 1 с через единичную площадку, перпендикулярную скорости волны.
Слайд 10Электромагнитные волны в диэлектриках
– уравнения Максвелла в среде
– материальные уравнения
– граничные
условия
(в отсутствии сторонних зарядов и токов проводимости)
(в отсутствии сторонних зарядов и токов проводимости)
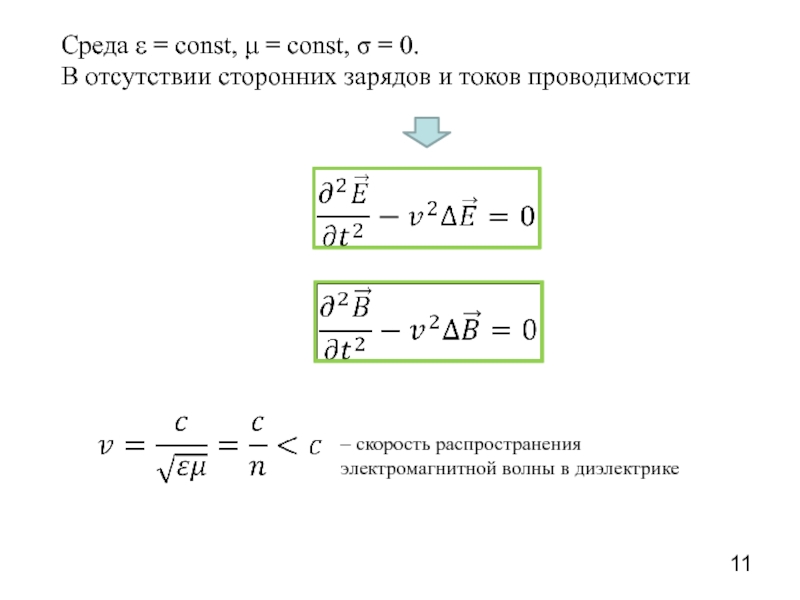
Слайд 11Среда ε = const, μ = const, σ = 0.
В отсутствии
сторонних зарядов и токов проводимости
– скорость распространения
электромагнитной волны в диэлектрике
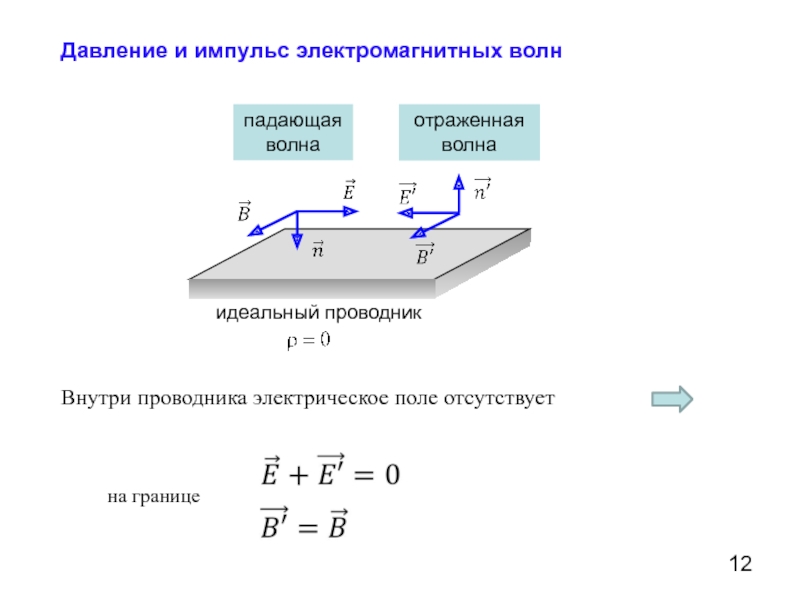
Слайд 12Давление и импульс электромагнитных волн
Внутри проводника электрическое поле отсутствует
на границе
падающая
волна
отраженная
волна
идеальный проводник
Слайд 13электромагнитная волна обладает импульсом
Давление оказывает магнитное поле
, w – объемная плотность
энергии падающей волны
Слайд 15Излучение электромагнитных волн. Вибратор Герца
– вибратор Герца (электрический диполь, момент которого
изменяется
со временем)
Слайд 17
Основные законы геометрической оптики
Закон прямолинейного распространения света
В однородной среде свет распространяется
по прямым линиям.
Закон теряет силу в явлениях дифракции света.
Закон теряет силу в явлениях дифракции света.
Закон независимости световых пучков
Действие световых пучков является независимым, т.е. суммарный эффект представляет собой сумму вкладов каждого светового пучка в отдельности.
Закон теряет силу в явлениях интерференции света.
Геометрическая оптика
Слайд 18
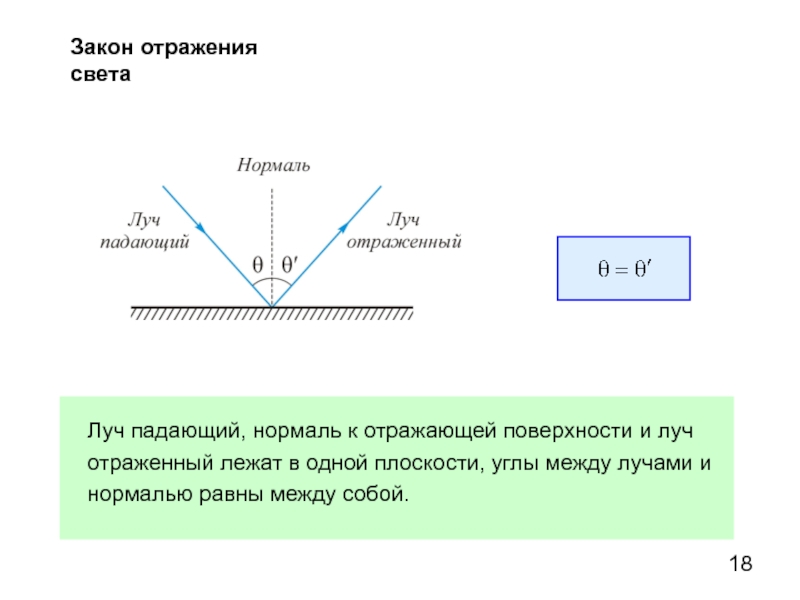
Закон отражения света
Луч падающий, нормаль к отражающей поверхности и луч
отраженный лежат в одной плоскости, углы между лучами и нормалью равны между собой.
Слайд 19
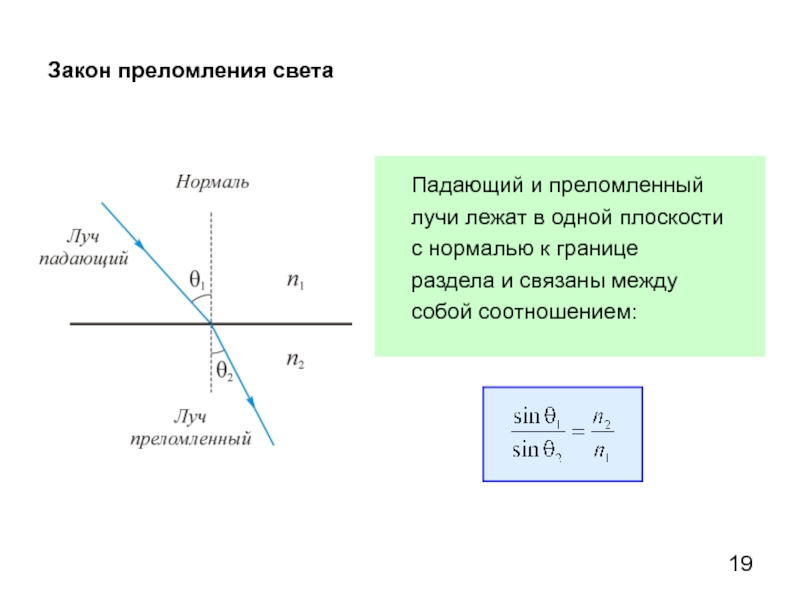
Закон преломления света
Падающий и преломленный лучи лежат в одной плоскости
с нормалью к границе раздела и связаны между собой соотношением:
Слайд 20
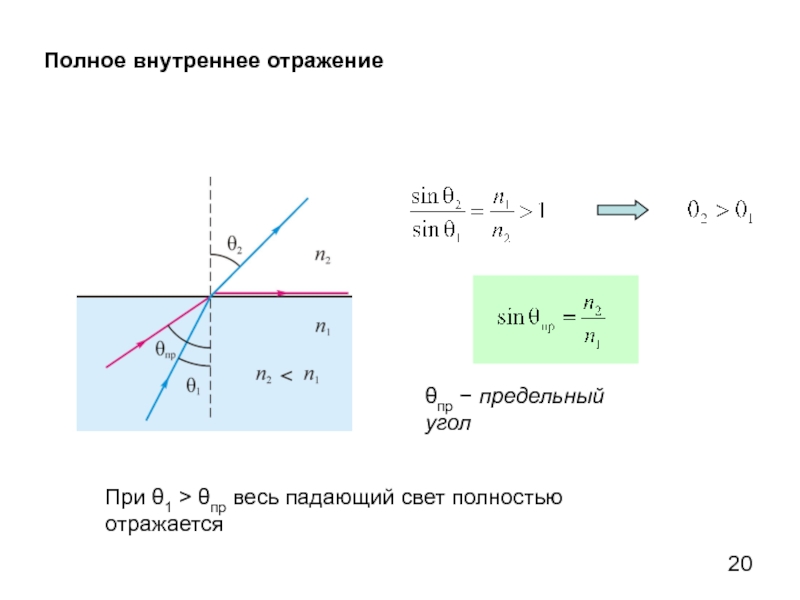
Полное внутреннее отражение
θпр − предельный угол
При θ1 > θпр весь
падающий свет полностью отражается
Слайд 21
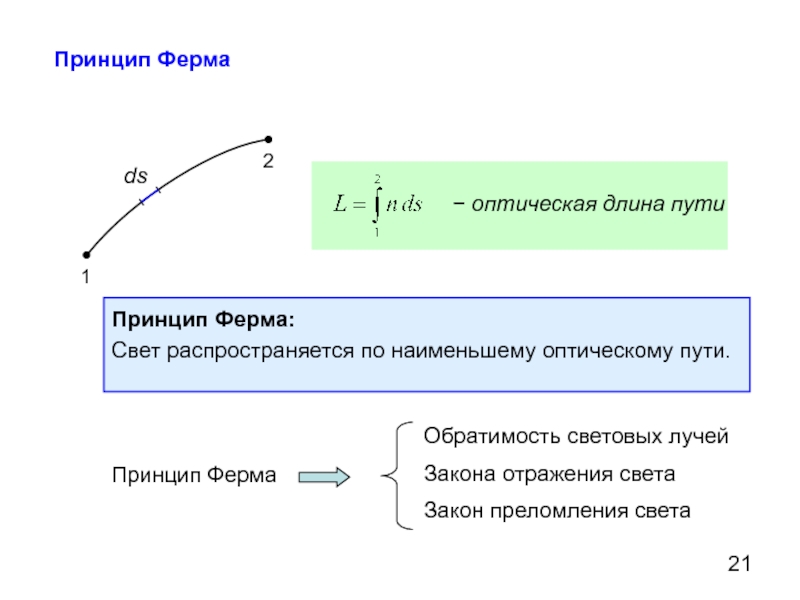
Принцип Ферма
1
2
ds
− оптическая длина пути
Принцип Ферма:
Свет распространяется по наименьшему оптическому
пути.
Принцип Ферма
Обратимость световых лучей
Закона отражения света
Закон преломления света
Слайд 22
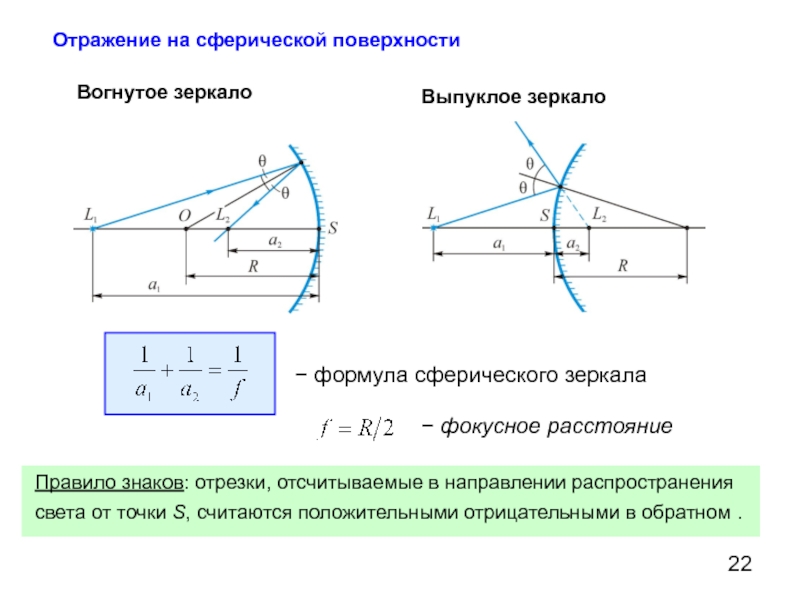
Отражение на сферической поверхности
Вогнутое зеркало
− формула сферического зеркала
− фокусное расстояние
Правило
знаков: отрезки, отсчитываемые в направлении распространения света от точки S, считаются положительными отрицательными в обратном .
Выпуклое зеркало
Слайд 24
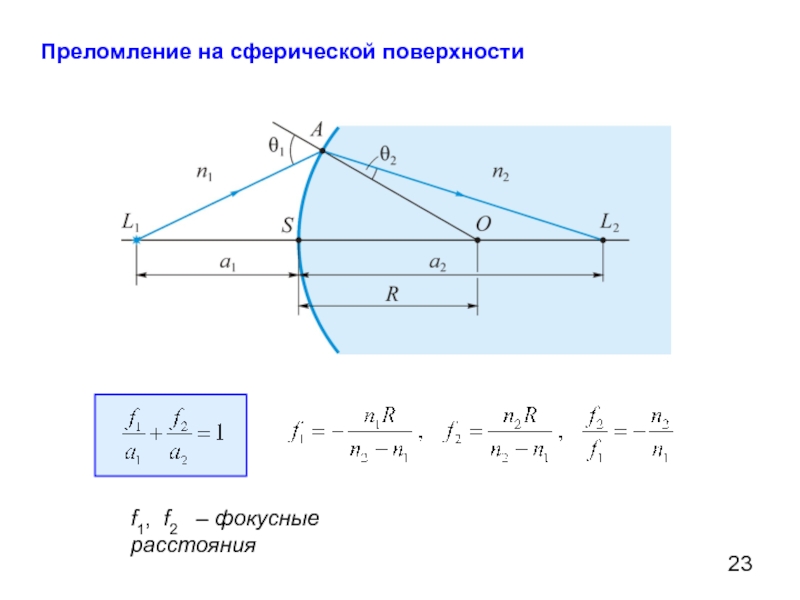
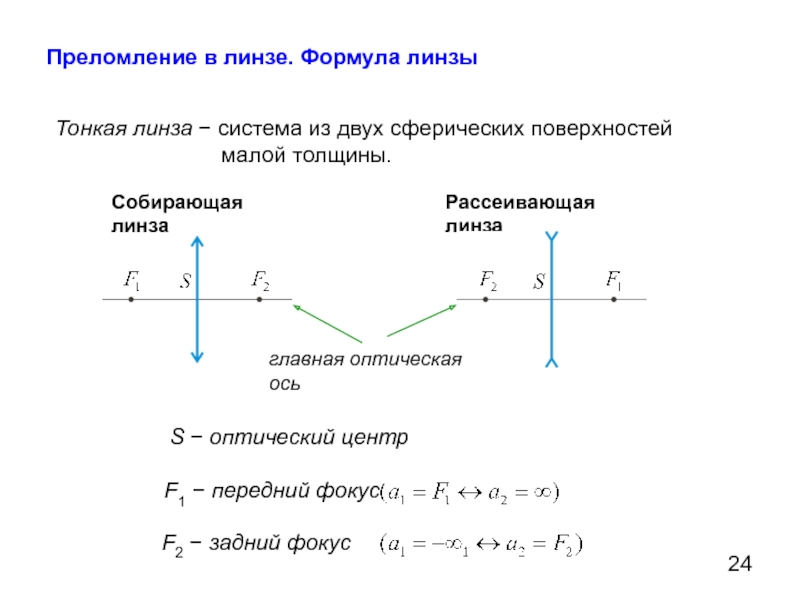
Преломление в линзе. Формула линзы
Тонкая линза − система из двух сферических
поверхностей
малой толщины.
Собирающая линза
Рассеивающая линза
главная оптическая ось
F1 − передний фокус
F2 − задний фокус
S − оптический центр
Слайд 25
a1 − расстояние до источника, a2 − расстояние до изображения
−
формула линзы
f > 0 − собирающая линза, f < 0 − рассеивающая линза
− фокусное расстояние линзы
Слайд 26
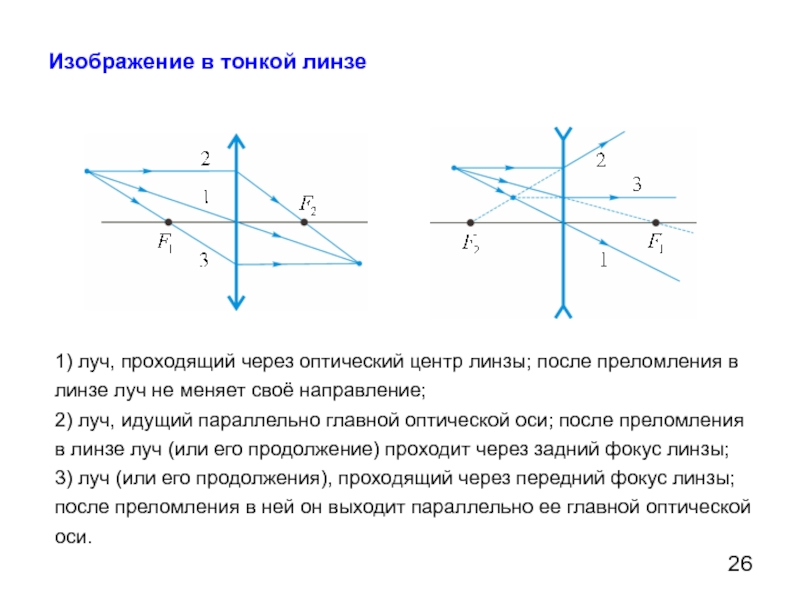
Изображение в тонкой линзе
1) луч, проходящий через оптический центр линзы; после преломления
в линзе луч не меняет своё направление;
2) луч, идущий параллельно главной оптической оси; после преломления в линзе луч (или его продолжение) проходит через задний фокус линзы;
3) луч (или его продолжения), проходящий через передний фокус линзы; после преломления в ней он выходит параллельно ее главной оптической оси.
2) луч, идущий параллельно главной оптической оси; после преломления в линзе луч (или его продолжение) проходит через задний фокус линзы;
3) луч (или его продолжения), проходящий через передний фокус линзы; после преломления в ней он выходит параллельно ее главной оптической оси.
