- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электрические цепи однофазного переменного тока. (Лекция 3) презентация
Содержание
- 1. Электрические цепи однофазного переменного тока. (Лекция 3)
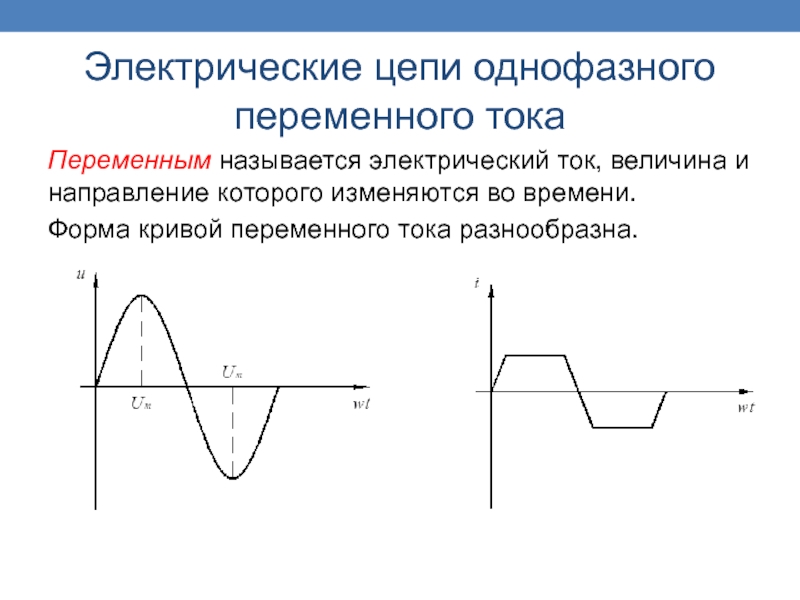
- 2. Переменным называется электрический ток, величина и направление
- 3. Значение переменного тока в рассматриваемый момент времени
- 4. Периодические токи, изменяющиеся по синусоидальному закону, называются
- 5. Частота – ток и напряжение меняют свое направление (в секунду)
- 6. Если у синусоидальных токов начальные фазы при
- 7. Действующим значением переменного тока называется среднеквадратичное значение
- 8. Законы Ома и Кирхгофа справедливы для мгновенных
- 9. При расчете электрических цепей часто приходится складывать
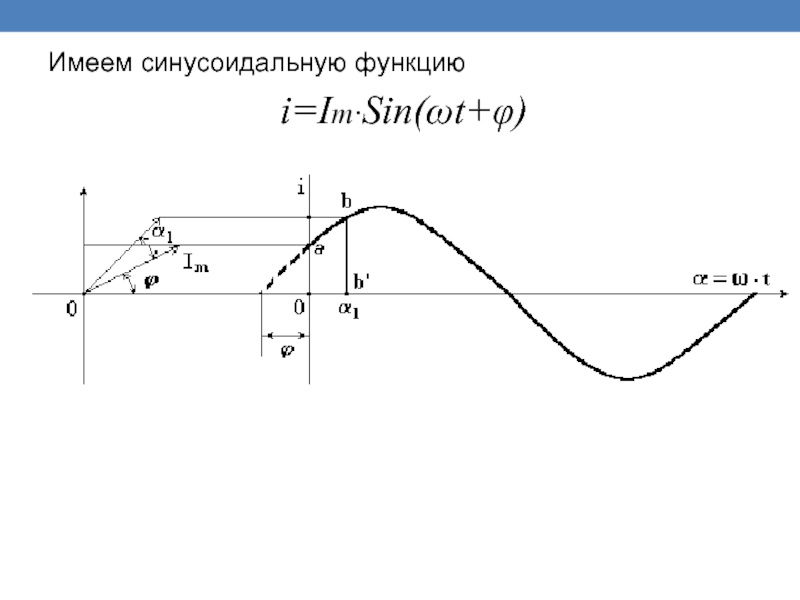
- 10. Имеем синусоидальную функцию i=Im·Sin(ωt+φ)
- 11. Пусть даны два синусоидальных тока:
- 12. Необходимо отметить, что напряжение, ток и ЭДС
- 13. При расчетах цепей синусоидального тока используют символический
- 14. Из курса математики известно, что комплексное число
- 15. С помощью формулы Эйлера можно перейти от
- 16. Комплексное число может быть представлено в виде
- 17.
- 18.
- 19.
- 20.
- 21. Замечание. В электротехнике над символами, изображающими комплексные
- 22. Спасибо за внимание!
Слайд 2Переменным называется электрический ток, величина и направление которого изменяются во времени.
Форма
Электрические цепи однофазного переменного тока
Слайд 3Значение переменного тока в рассматриваемый момент времени называют мгновенным значением и
Мгновенный ток называется периодическим, если значения его повторяются через одинаковые промежутки времени:
Наименьший промежуток времени, через который значения переменного тока повторяются, называется периодом.
Период T измеряется в секундах [с].
Слайд 4Периодические токи, изменяющиеся по синусоидальному закону, называются синусоидальными.
Мгновенное значение синусоидального тока
где Im - максимальное, или амплитудное, значение тока.
Амплитудное значение синусоидального тока или напряжения можно измерить с помощью осциллографа.
Аргумент синусоидальной функции
- называют фазой.
Слайд 6Если у синусоидальных токов начальные фазы при одинаковых частотах одинаковы, говорят,
Если неодинаковы по фазе, говорят, что токи сдвинуты по фазе.
Сдвиг фаз двух синусоидальных токов измеряется разностью начальных фаз:
Амперметры и вольтметры электромагнитной системы измеряют действующие значения переменного тока и напряжения.
Слайд 7Действующим значением переменного тока называется среднеквадратичное значение тока за период.
Действующее значение
можно определить, как:
Аналогично определяются действующие значения ЭДС и напряжений…
.
Слайд 8Законы Ома и Кирхгофа справедливы для мгновенных значений токов и напряжений.
.
Законы Кирхгофа для мгновенных значений:
,
.
Слайд 9При расчете электрических цепей часто приходится складывать или вычитать величины токов
Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими.
Задача упрощается, если представить наши синусоидальные функции в векторной форме.
Изображения синусоидальных функций времени
в векторной форме
Слайд 11Пусть даны два синусоидальных тока:
Нужно сложить эти токи и получить результирующий
Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.
Слайд 12Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а
Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус - векторов, вращающихся с одинаковой угловой скоростью.
Изображать на векторной диаграмме два вектора, вращающихся с различной угловой скоростью, бессмысленно.
Положительным считается направление вращения векторов против часовой стрелки.
Векторные диаграммы используются для качествен-ного анализа электрических цепей, а также при решении некоторых электротехнических задач.
Слайд 13При расчетах цепей синусоидального тока используют символический метод расчета или метод
В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам.
Изображение синусоидальных функций времени
в комплексной форме
Слайд 14Из курса математики известно, что комплексное число может быть записано в
где с - модуль комплексного числа; φ - аргумент;
a - вещественная часть комплексного числа;
b - мнимая часть;
j - мнимая единица, j = .
Слайд 15С помощью формулы Эйлера можно перейти от показательной формы записи к
От алгебраической формы записи переходят к показательной форме с помощью формул:
Слайд 16Комплексное число может быть представлено в виде радиус - вектора в
Вектор длиной, равной модулю с, расположен в начальный момент времени под углом φ относительно вещественной оси
Слайд 21Замечание. В электротехнике над символами, изображающими комплексные напряжения, токи, ЭДС, принято
Синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью ω.
Проекция вектора на мнимую ось изменяется по синусоидальному закону.
Законы Ома и Кирхгофа в комплексной форме:
- закон Ома;
- первый закон Кирхгофа;
- второй закон Кирхгофа.