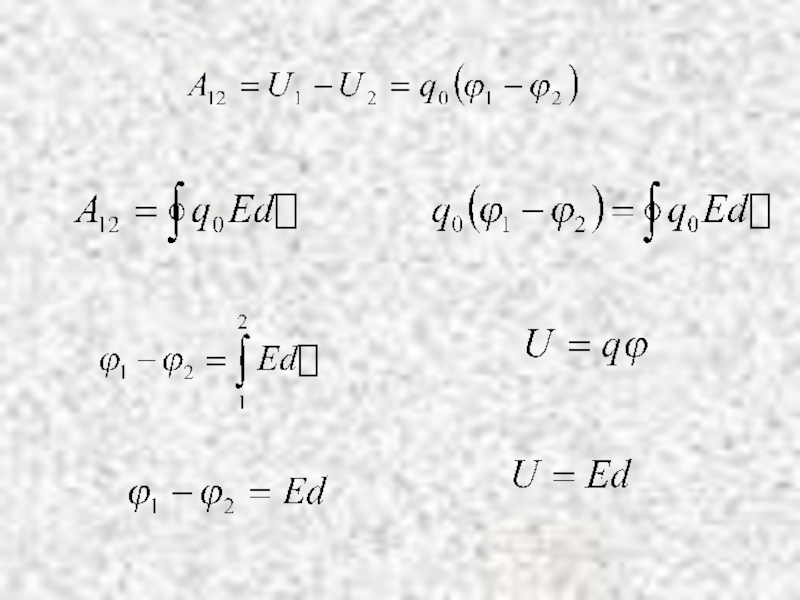- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электр зарядының сақталу заңы презентация
Содержание
- 1. Электр зарядының сақталу заңы
- 2. Жоспары 1.Электр зарядының сақталу заңы. 2.Кулон
- 3. Электр зарядының сақталу заңы Зерттеу жұмыстарында (1910—1914)
- 4. Зерттеу жұмыстардың нәтижесінде фундаменталды табиғат заңы ашылды,
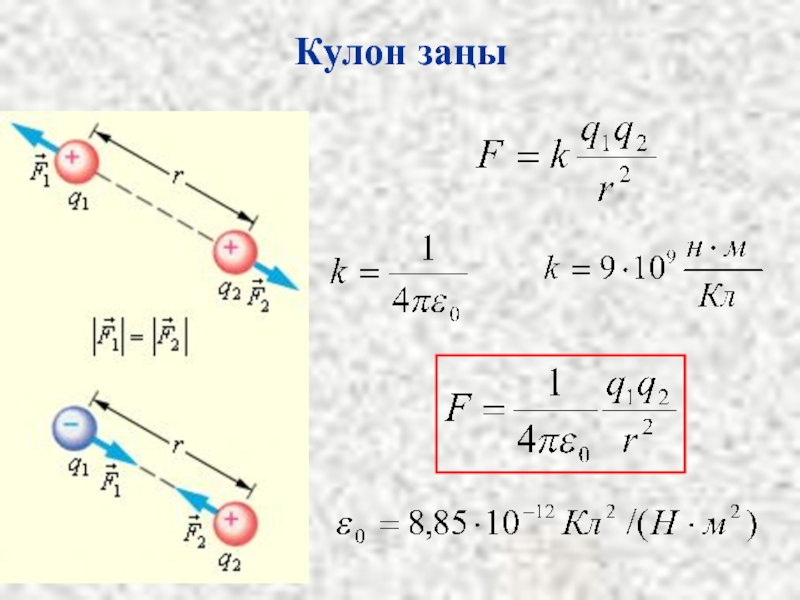
- 5. Кулон заңы
- 6. Электростатикалық өріс. Электростатикалық өрістің кернеулігі.
- 7. Электростатикалық өрісті графикалық түрде кернеулік сызықтары арқылы
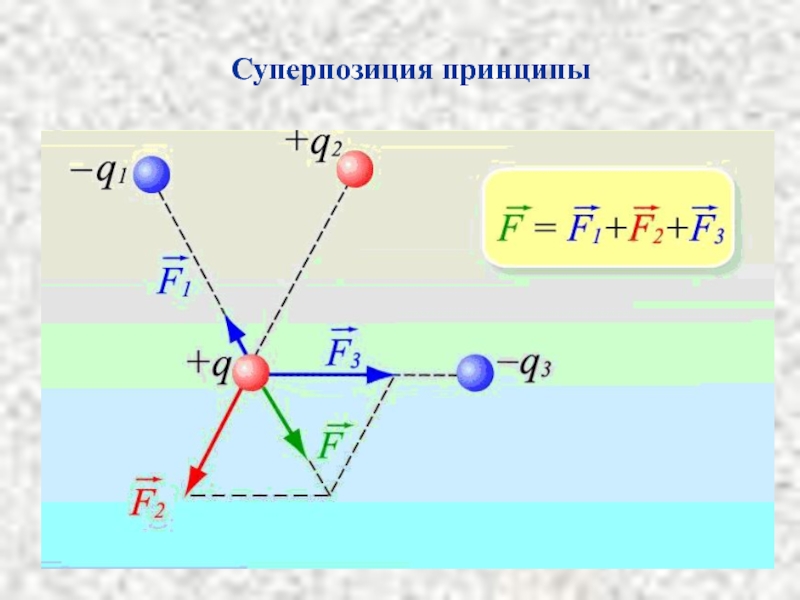
- 9. Суперпозиция принципы
- 10. Егер өріс бірлік зарядтан турса, онда кернеулік
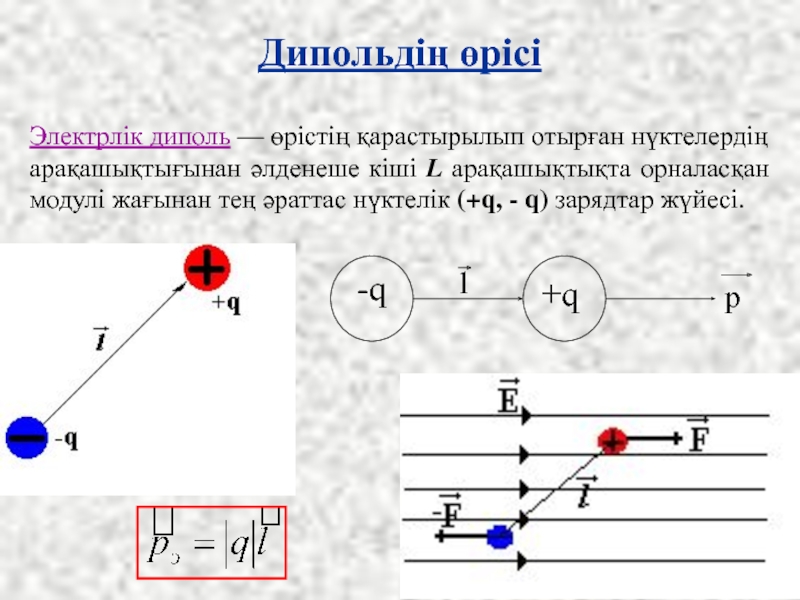
- 11. Дипольдің өрісі Электрлік диполь — өрістің қарастырылып
- 12. Суретте суперпозиция принципінің қолданылуы мысалы ретінде l
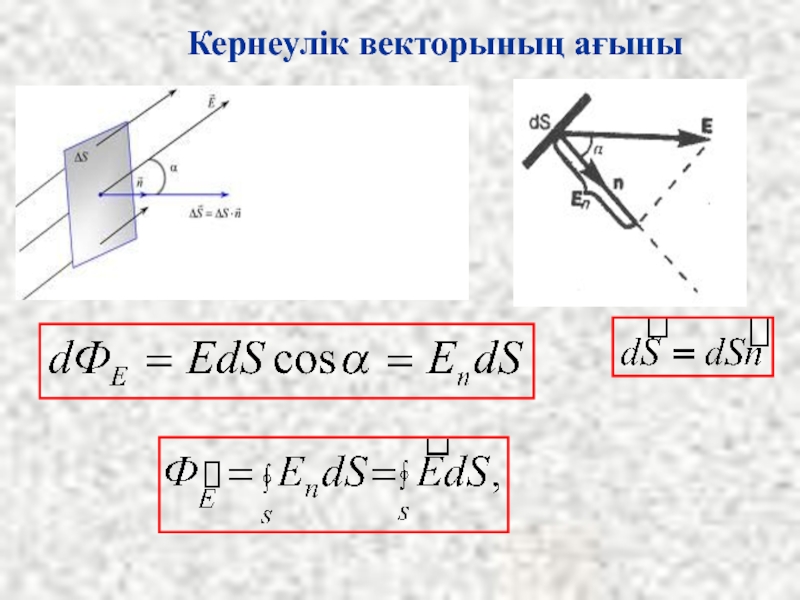
- 13. Кернеулік векторының ағыны
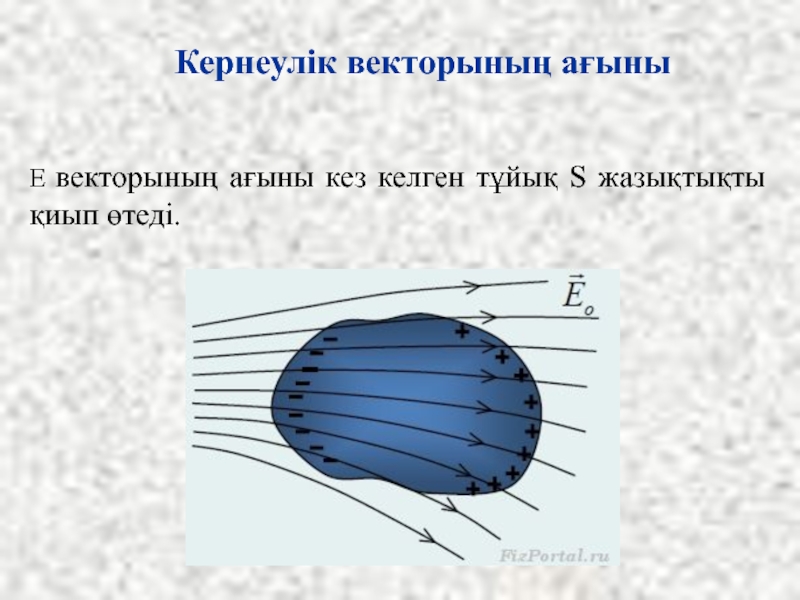
- 14. Е векторының ағыны кез келген тұйық
- 15. Кернеулік векторының ағыны
- 16. Тұйық және нүктелік q зарядтан тұратын кез
- 17. Гаусса теоремасын мына түрде жазуға болады:
- 18. Кейбір вакуумдағы электростатикалық өрістерді есептеу үшін Гаусс теоремасын қолдану.
- 19. Біртекті зарядталған шексіз жазықтық өрісі.
- 20. Екі шексіз өзара параллель зарядталған жазықтықтардың
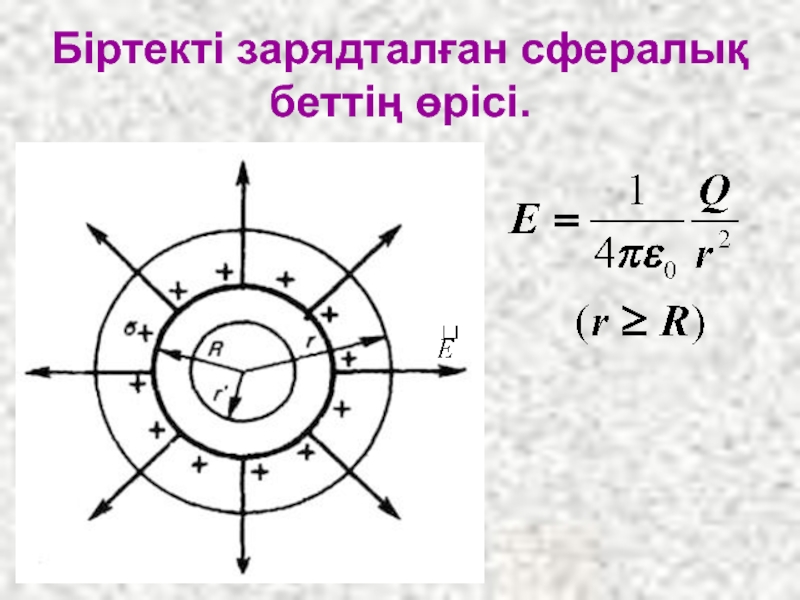
- 21. Біртекті зарядталған сфералық беттің өрісі.
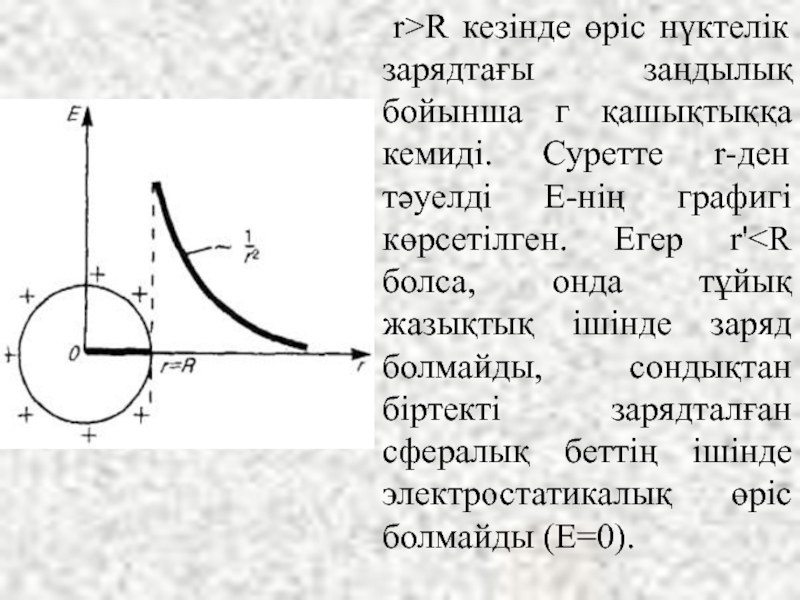
- 22. r>R кезінде өріс нүктелік зарядтағы
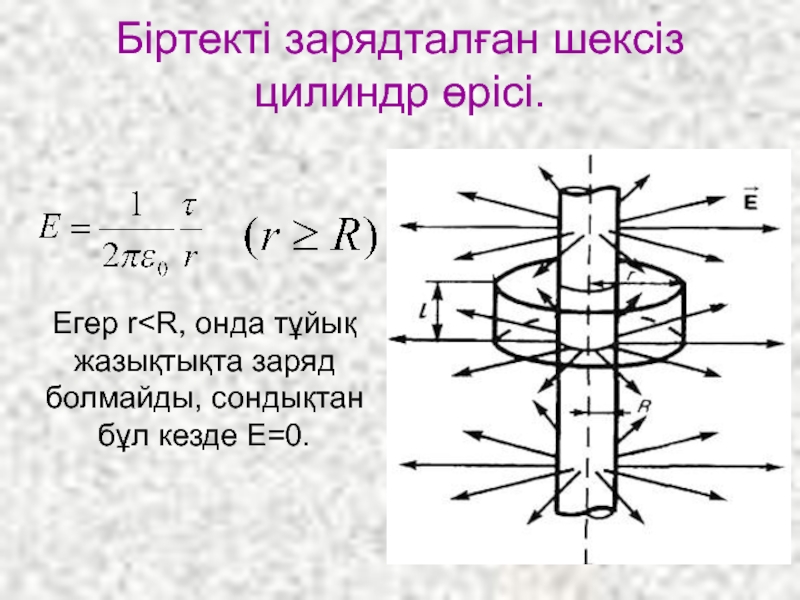
- 23. Біртекті зарядталған шексіз цилиндр өрісі. Егер r
- 24. Электростатикалық өріс потенциалдық болып табылады.
- 25. яғни бастапқы және соңғы нүктелердегі потенциалдарының айырмасын
- 26. Сонымен қатар 1 нүктесіне 2
- 27. Бағытталған электростатикалық өрістің кернеулік векторының циркуляциясы:
- 28. Электр өріс потенциалы
- 30. Электр өрісінің кернеулігі мен φ потенциал арасындағы
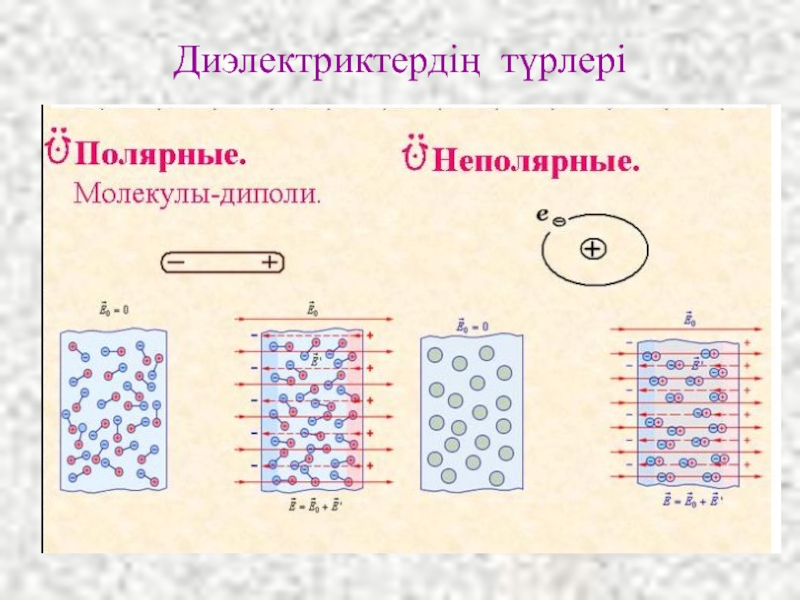
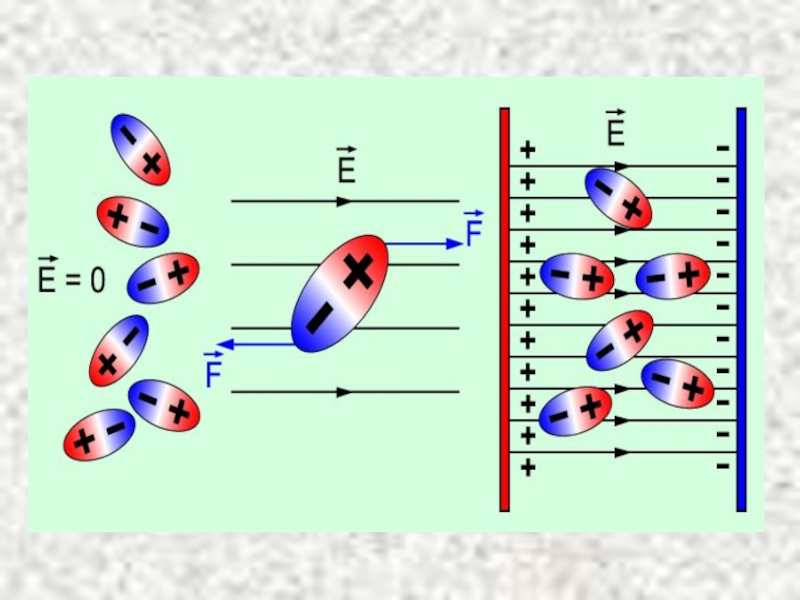
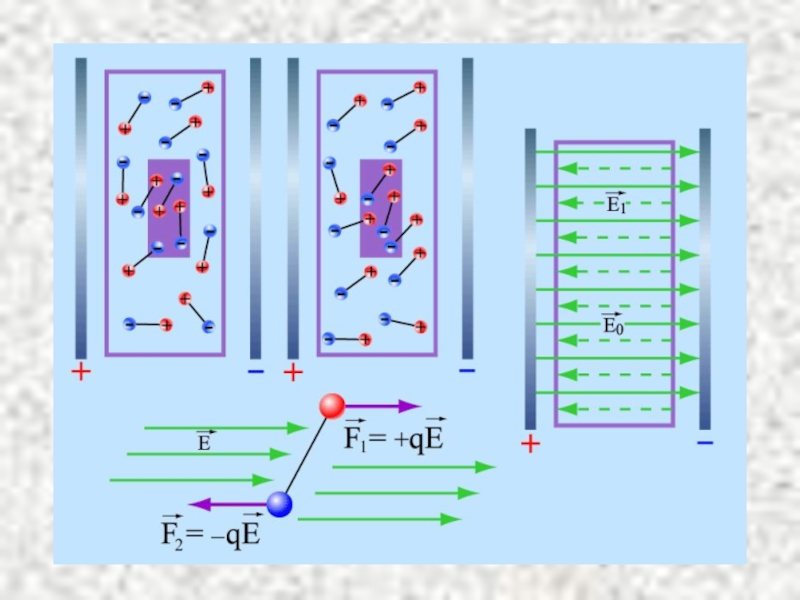
- 31. Диэлектриктердің түрлері
- 35. Электр ығысу векторы Диэлектриктегі электростатикалық өріс үшін Гаусс теоремасы
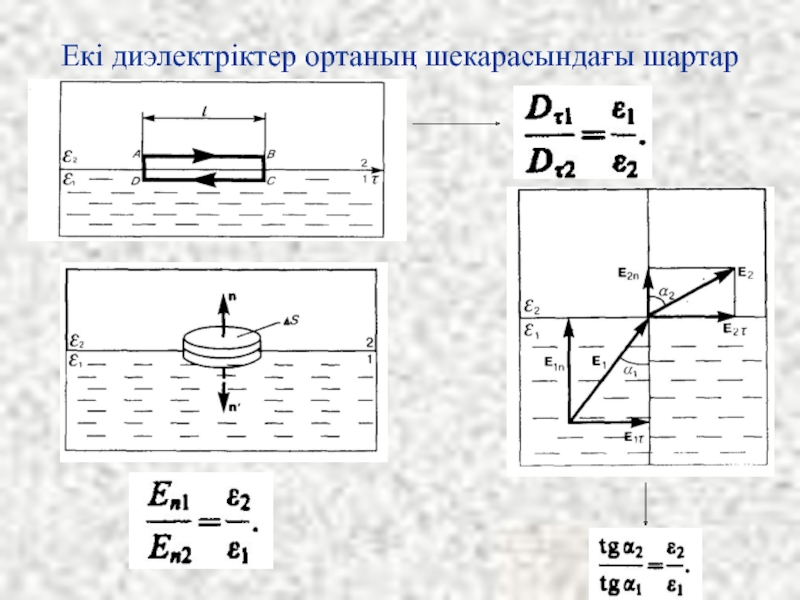
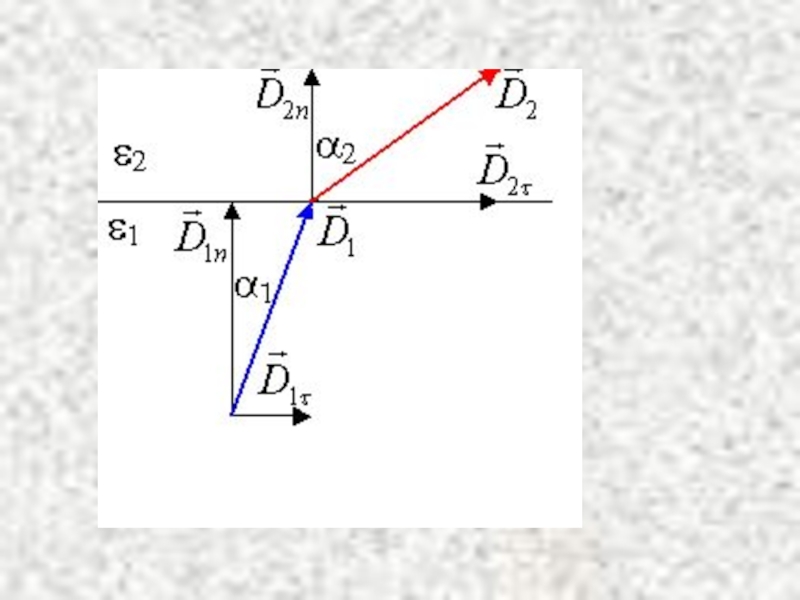
- 36. Екі диэлектріктер ортаның шекарасындағы шартар
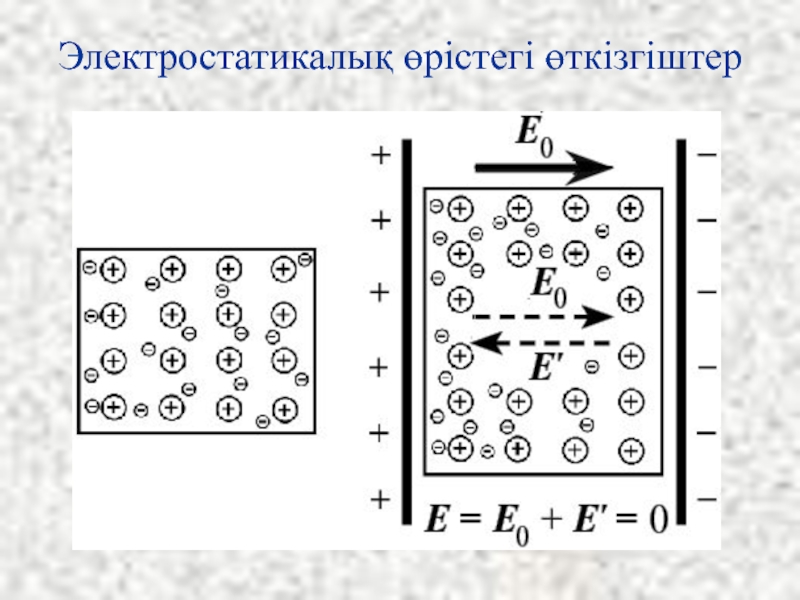
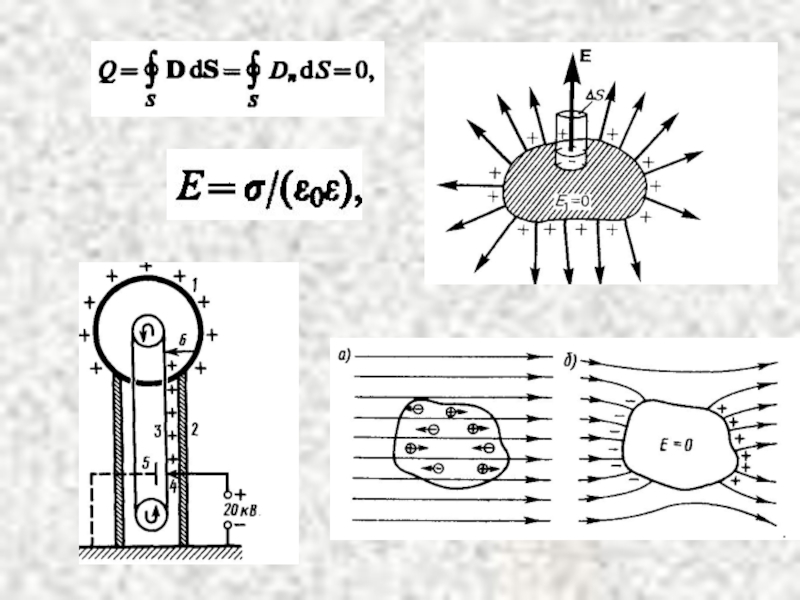
- 38. Электростатикалық өрістегі өткізгіштер
- 40. Электросыйымдылық
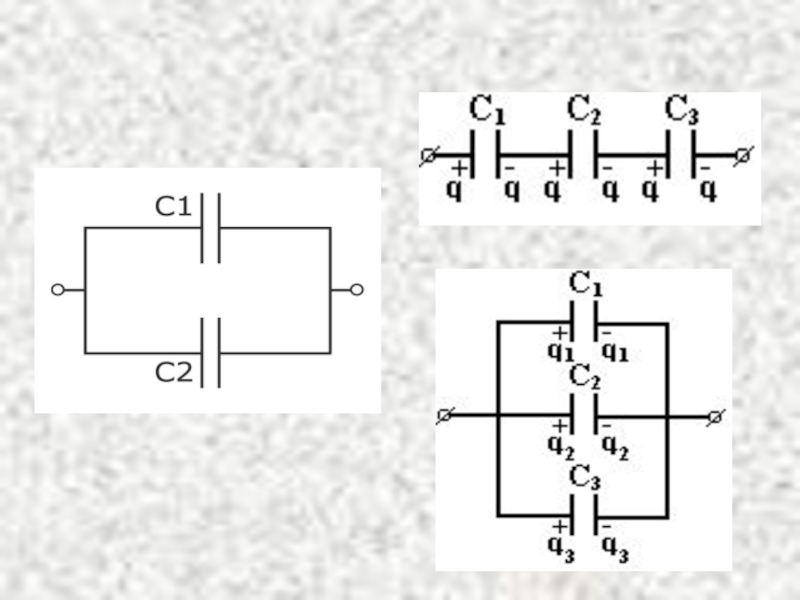
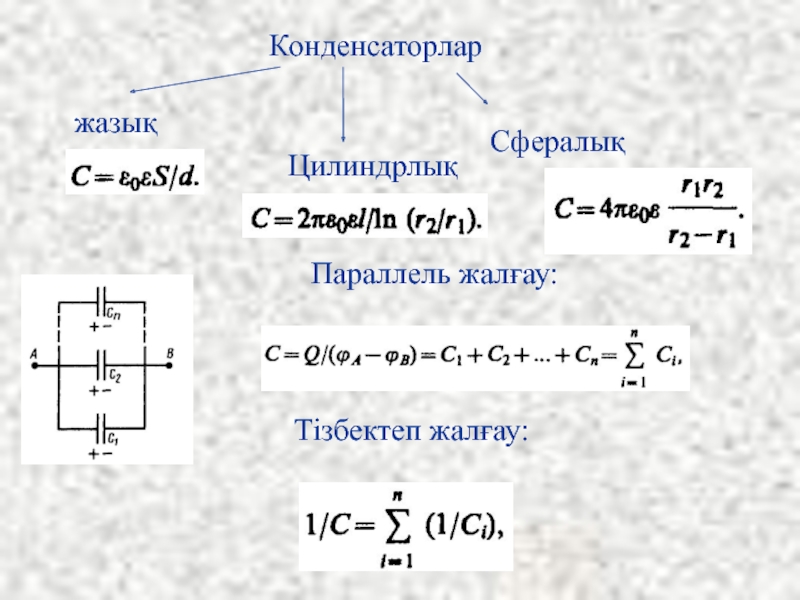
- 42. Конденсаторлар жазық Цилиндрлық Сфералық Параллель жалғау: Тізбектеп жалғау:
- 43. Электростатикалық өріс энергиясы
- 44. ДӘРІСТІҢ СОҢЫ
Жоспары 1.Электр зарядының сақталу заңы. 2.Кулон заңы. 3.Электр өрісі. Электр өрісінің кернеулілігі. 4.Кернеулік векторының ағыны. 5.Вакуумдағы электр өрісі үшін Остроградский-Гаусс теоремасы. . 6. Электр өрісінің күшінің жұмысы. 7.
Слайд 2Жоспары
1.Электр зарядының сақталу заңы.
2.Кулон заңы.
3.Электр өрісі. Электр өрісінің кернеулілігі.
4.Кернеулік векторының ағыны.
5.Вакуумдағы электр өрісі үшін Остроградский-Гаусс теоремасы. .
6. Электр өрісінің күшінің жұмысы.
7. Циркуляция.
8.Потенциал.
8.Потенциалдық электр өрісінің кернеулігімен байланысы.
5.Вакуумдағы электр өрісі үшін Остроградский-Гаусс теоремасы. .
6. Электр өрісінің күшінің жұмысы.
7. Циркуляция.
8.Потенциал.
8.Потенциалдық электр өрісінің кернеулігімен байланысы.
Слайд 3Электр зарядының
сақталу заңы
Зерттеу жұмыстарында (1910—1914) американдық физик Р. Милликен (1868—1953) электр
зарядының дискретті, яғни кез келген дененің заряды q элементар электр зарядынан тұратынын көрсетті.
е=1,6∙10-19 Кл
me=9,11∙10-31 кг
Слайд 4Зерттеу жұмыстардың нәтижесінде фундаменталды табиғат заңы ашылды, 1843ж. ағылшын физигі М.
Фарадей тәжірибе жүзінде электр зарядының сақталу заңын тұжырымдады:
Электр зарядының өлшем бірлігі — кулон (Кл) — бұл ток күші 1 А болғанда, өткізгіштің көлденең қимасынан 1 с уақытта өтетін электр заряды.
Кез келген тұйық жүйеде барлық бөлшектер зарядтарының алгебралық қосындысы өзгеріссіз қалады .
Слайд 6Электростатикалық өріс.
Электростатикалық өрістің кернеулігі.
Берілген нүктедегі Электростатикалық өрістің кернеулігі
өрістің осы нүктесінде орналасқан бірлік оң зарядқа әсер ететін күшпен анықталатын физикалық шама болып табылады.
Е векторының бағыты сол өрістегі оң зарядқа әсер ететін күштің бағытымен сәйкес келеді. Егер өріс оң зарядтан турса, онда Е векторы радиус-вектордың бойымен зарядтан сыртқы ортаға бағытталады (оң зарядтан тебіледі); егер өріс теріс зарядтан турса, онда Е векторы зарядқа қарай бағытталады.
Вакуумдағы нүктелік заряд өрісінің кернеулігі
немесе
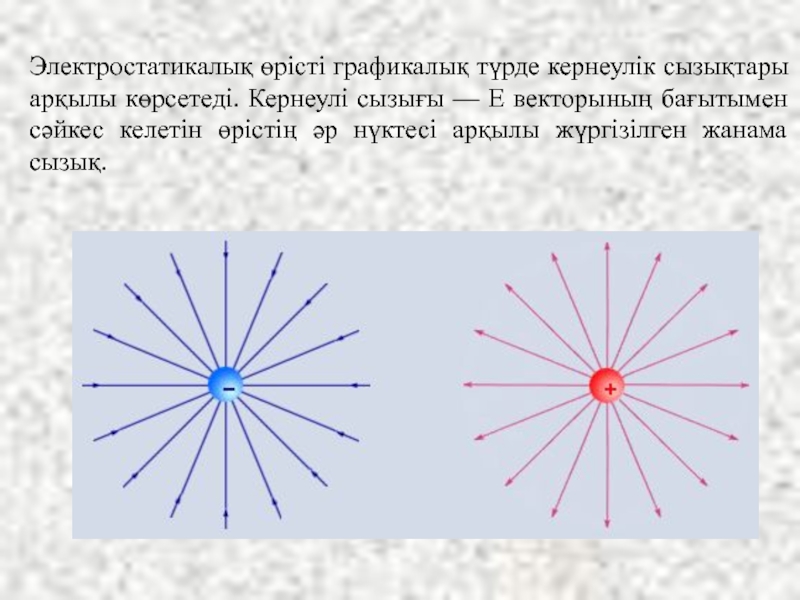
Слайд 7Электростатикалық өрісті графикалық түрде кернеулік сызықтары арқылы көрсетеді. Кернеулі сызығы —
Е векторының бағытымен сәйкес келетін өрістің әр нүктесі арқылы жүргізілген жанама сызық.
Слайд 10Егер өріс бірлік зарядтан турса, онда кернеулік сызықтары — түзу, егер
оң заряд болса, зарядтан шығады, егер теріс заряд болса,сол зарядқа кіреді.
Слайд 11Дипольдің өрісі
Электрлік диполь — өрістің қарастырылып отырған нүктелердің арақашықтығынан әлденеше кіші
L арақашықтықта орналасқан модулі жағынан тең әраттас нүктелік (+q, - q) зарядтар жүйесі.
-q
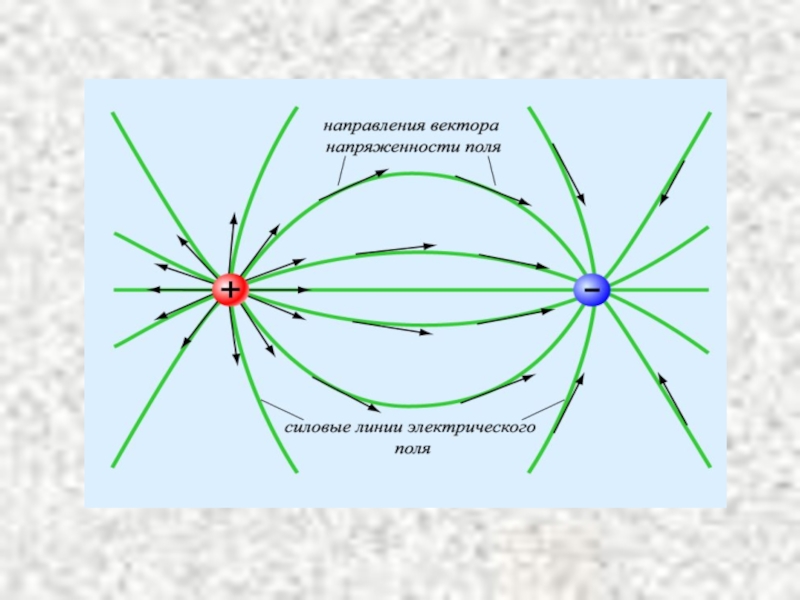
Слайд 12Суретте суперпозиция принципінің қолданылуы мысалы ретінде l арақашықтықта орналасқан модулі жағынан
бірдей, заряды q және –q жүйе –электрлік диполь өрісінің күш сызықтары көрсетілген.
Электрлік диполь өрісінің
күш сызықтары
Слайд 16Тұйық және нүктелік q зарядтан тұратын кез келген формадағы жазықтық үшін
Е векторы q/ε0 тең болады, яғни
Вакуумдағы электростатикалық өріс үшін Гаусс теоремасы
Ағынның таңбасы q зарядының таңбамен сәйкес келеді.
К. Гаусс теоремасы кез келген тұйық жазықтық арқылы өтетін злектр өрісінің кернеулік векторының ағынын анықтайды.
Слайд 22 r>R кезінде өріс нүктелік зарядтағы заңдылық бойынша г қашықтыққа
кемиді. Суретте r-ден тәуелді Е-нің графигі көрсетілген. Егер r'
Слайд 24 Электростатикалық өріс потенциалдық болып табылады.
Электростатикалық өріс күшінің жұмысын q
зарядының өрісінің бастапқы және соңғы нүктелеріндегі q0 нүктелік зарядтың потенциалдық энергиясының айырымы ретінде көрсетуге болады :
1 нүктесінен 2 нүктесіне орын ауыстырған q0 зарядтың өріс күшінің жұмысы мына түрде де жазыла алады:
A12=U1- U2=q0(φ1 - φ2).
1 нүктесінен 2 нүктесіне орын ауыстырған q0 зарядтың өріс күшінің жұмысы мына түрде де жазыла алады:
A12=U1- U2=q0(φ1 - φ2).
Слайд 25яғни бастапқы және соңғы нүктелердегі потенциалдарының айырмасын орын ауыстырған заряд шамасына
көбейткенге тең. Электр өрісінің 1 және 2 нүктелерінің потенциалдарының айырмасы бірлік оң зарядтың өріс күшінің әсерінен 1 нүктесінен 2 нүктесіне орын ауыстырғанда істелетін жұмыс шамасымен анықталады.
Слайд 26 Сонымен қатар 1 нүктесіне 2 нүктесіне электростатикалық өріс күшінің
әсерінен орын ауыстырған q0 зарядтың жұмысы мына түрде беріле алады :
Слайд 30Электр өрісінің кернеулігі мен φ потенциал арасындағы байланыс.
Декарттық координат жүйесінде:
Егер өріс
біртекті және Х осі бойымен бағытталса, онда:
