- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение тела вокруг неподвижной точки под действием силы тяжести. Случай Лагранжа презентация
Содержание
- 1. Движение тела вокруг неподвижной точки под действием силы тяжести. Случай Лагранжа
- 2. 1. Уравнения Пуассона неподвижная система координат подвижная
- 3. 2. Динамические уравнения Эйлера при наличии силы
- 4. 3. Уравнения движения тяжелого твердого тела вокруг
- 5. 4. Первые интегралы системы 1) 2)
- 6. 5. Известные случаи интегрируемости А) Случай Эйлера:
- 7. 6. Вывод уравнения для угла нутации в
- 8. 7. Качественный анализ движения ТТ в случае
- 9. 8. Быстро вращающееся тело: псевдорегулярная прецессия Начальные
- 10. 9. О пользе анализа размерностей Доказательство теоремы
Слайд 1ДИНАМИКА ТВЕРДОГО ТЕЛА
ЛЕКЦИЯ 8:
ДВИЖЕНИЕ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ
Слайд 21. Уравнения Пуассона
неподвижная система координат
подвижная система координат (ПСС), жестко связанная с
центр тяжести
единичный вектор верт. оси OZ
в ПСС
Уравнения Пуассона
Выражение компонент орта через углы Эйлера
Слайд 32. Динамические уравнения Эйлера при наличии силы тяжести
Динамические уравнения Эйлера в
Динамические уравнения Эйлера для движения тяжелого твердого тела
Слайд 43. Уравнения движения тяжелого твердого тела вокруг неподвижной точки
Замкнутая система уравнений
После нахождения
зависимости
находятся из условий
а оставшийся угол Эйлера
из одного из кинематических уравнений Эйлера
Слайд 54. Первые интегралы системы
1)
2) Теорема об изменении кинетического момента
Реакция опоры и
3) Сохранение энергии
Из общей теории множителя Якоби известно, что для того, чтобы интегрирование исходной системы можно было свести к квадратурам при любых начальных условиях, нужно найти еще один независимый от них интеграл.
Слайд 65. Известные случаи интегрируемости
А) Случай Эйлера: тело произвольно, но его центр
дополнительный интеграл
В) Случай Лагранжа: эллипсоид инерции тела для неподвижной точки является эллипсоидом вращения, а центр тяжести находится на оси вращения
дополнительный интеграл
С) Случай Ковалевской: эллипсоид инерции для точки О является эллипсоидом вращения вокруг оси Oz, момент инерции относительно этой оси вдвое меньше двух других, а центр тяжести тела лежит в экваториальной плоскости эллипсоида инерции
дополнительный интеграл
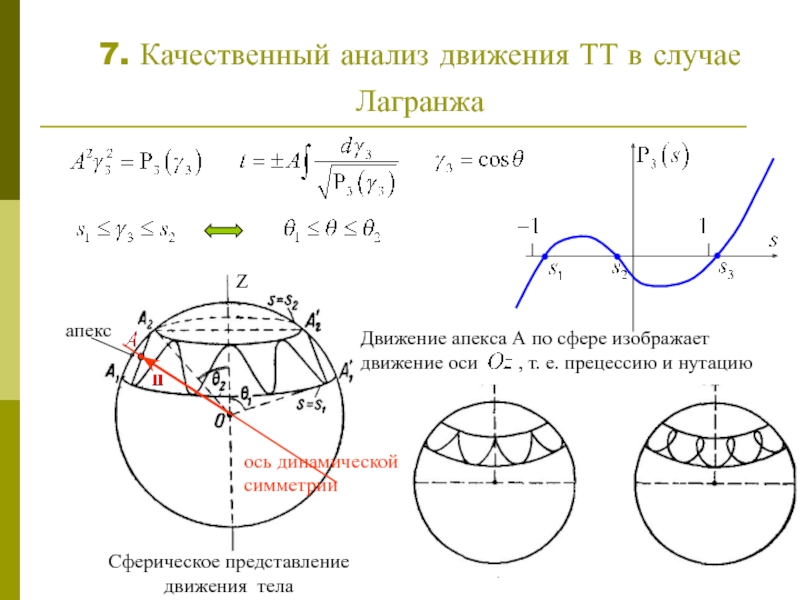
Слайд 87. Качественный анализ движения ТТ в случае Лагранжа
Сферическое представление движения
апекс
ось динамической симметрии
Движение апекса А по сфере изображает движение оси , т. е. прецессию и нутацию
Слайд 98. Быстро вращающееся тело: псевдорегулярная прецессия
Начальные условия
размерности
Аргументами должны являться
Быстро вращающееся тело – большие – малые значения параметра
случай Эйлера вращения симметричного тела
(регулярная прецессия)
Раскладывая в ряд Тейлора
точный результат
Когда велика, изменение угла нутации настолько мало, что прецессия кажется регулярной. Такая нерегулярная прецессия, мало отличающаяся от регулярной, называется псевдорегулярной прецессией.
Слайд 109. О пользе анализа размерностей
Доказательство теоремы Пифагора
Треугольник, а, значит, и его
размерности