- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Диполь. Поле диполя презентация
Содержание
- 1. Диполь. Поле диполя
- 2. 1.4. Диполь. Поле диполя.
- 3. Определение диполя. Определение. Система зарядов, состоящая из
- 4. По принципу суперпозиции:
- 5. Потенциал поля диполя.
- 6. Преобразование формулы.
- 7. Преобразование знаменателя.
- 8. Преобразование числителя.
- 9. Дипольный момент.
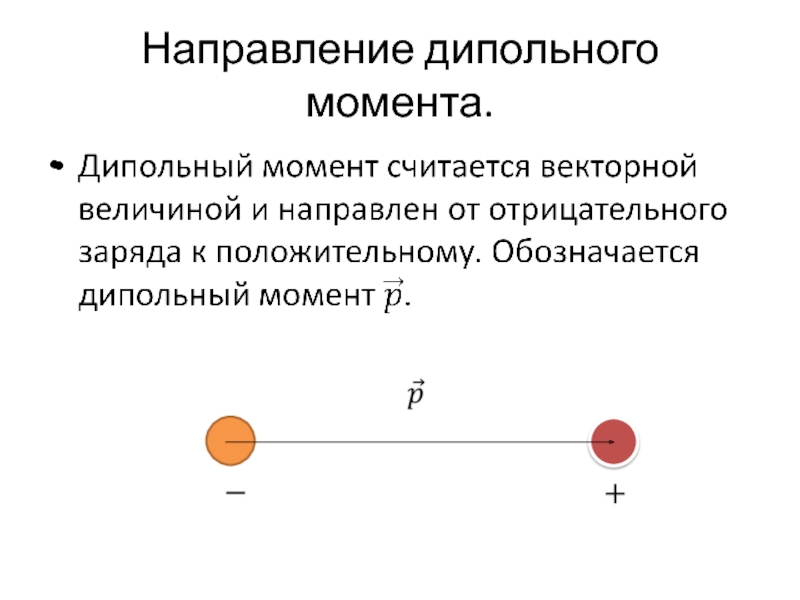
- 10. Направление дипольного момента.
- 11. Следствия из определения.
- 12. Потенциал поля диполя.
- 13. Потенциал поля диполя.
- 14. Напряжённость поля диполя.
- 15. Координата x напряжённости поля диполя.
- 16. Проекции напряжённости на другие оси.
- 17. Вектор напряжённости поля диполя.
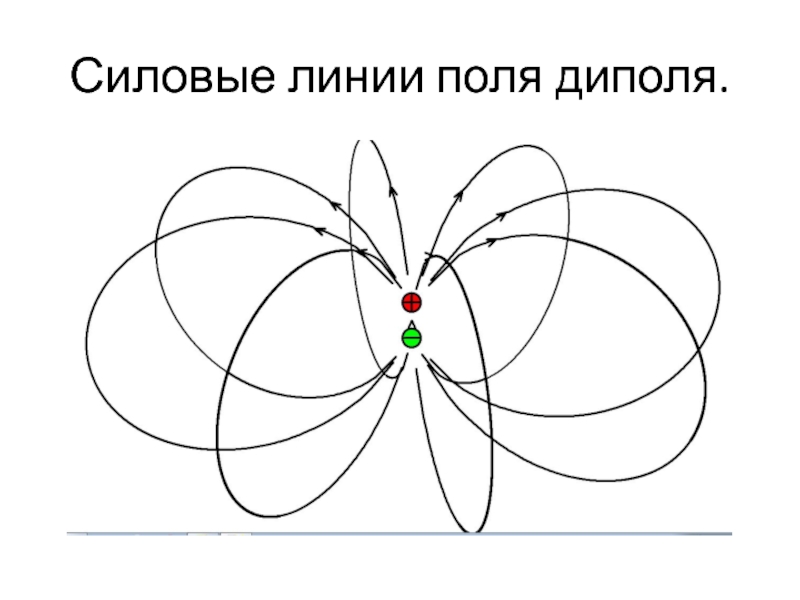
- 18. Силовые линии поля диполя.
- 19. Программа Progr D: Progr E: Progr F: Progr G: Progr H:
- 20. 1.5.Пондеромоторные силы. Определение. Пондеромоторными силами называются силы,
- 21. Сила, действующая на одиночный заряд
- 22. Сила, действующая на систему зарядов.
- 23. Сила, действующая на диполь. Предположим теперь, что
- 24. Равенство нулю сил.
- 25. Момент сил, действующих на диполь.
- 26. Модуль момента сил.
- 27. Равновесие диполя
- 28. Демонстрация поворота диполя в электрическом поле.
- 29. Энергия диполя в электрическом поле.
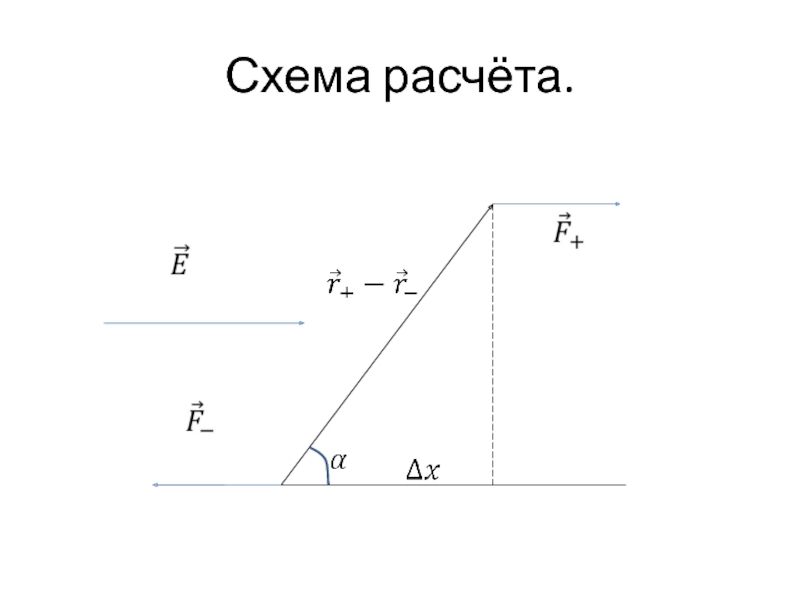
- 30. Схема расчёта.
- 31. Потенциальная энергия диполя.
- 32. Работа по перемещению пробного заряда.
- 33. Минимум и максимум потенциальной энергии диполя.
- 34. Сила, действующая на диполь в неоднородном поле.
- 35. Преобразование формул
- 36. Формула силы
- 37. Координаты силы
- 38. Диполь в неоднородном поле Рассмотрим самый распространённый
- 39. Проекция силы на ось ox
- 40. 1.6.Прямой расчёт поля системы зарядов. Часто система
- 41. Объёмная плотность заряда. Для характеристики распределения зарядов
- 42. Следствия из определения.
- 43. Схема расчёта
- 44. Элемент заряда
- 45. Элемент потенциала
- 46. Полный потенциал всей системы зарядов.
- 47. Поверхностная система зарядов. Расчёт поля с помощью
- 48. Поверхностная система зарядов Определение. Система зарядов, расположенная на некоторой поверхности, называется поверхностной системой зарядов.
- 49. Поверхностная плотность зарядов.
- 50. Следствия из определения.
- 51. Потенциал поверхностной системы зарядов.
- 52. Линейная система зарядов Определение. Система зарядов, расположенных на некоторой кривой линии, называется линейной системой зарядов.
- 53. Линейная плотность зарядов. Определение. Линейной плотностью заряда
- 54. Следствия из определения.
- 55. Потенциал линейной системы зарядов.
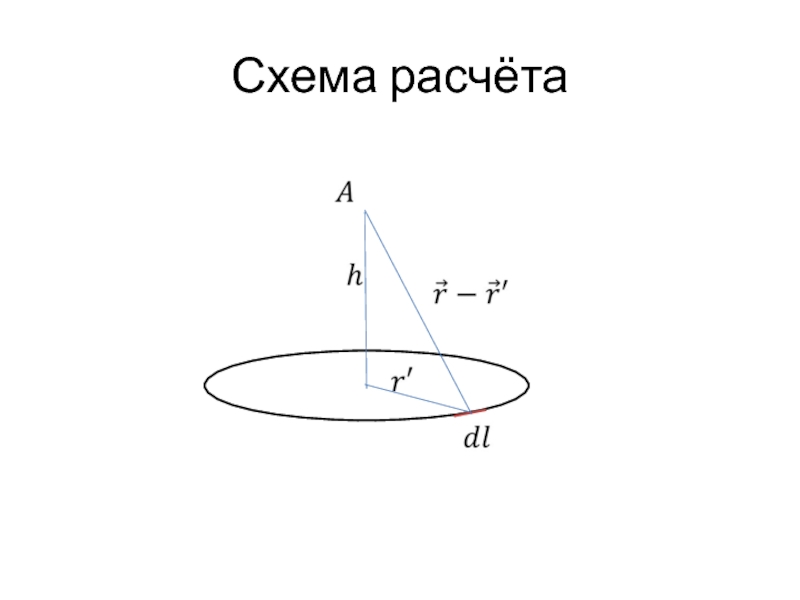
- 56. Потенциал поля заряженного кольца.
- 57. Схема расчёта
- 58. Преобразование формул
- 59. Поле в центре кольца.
- 60. Напряжённость поля кольца
- 61. Поле на больших расстояниях от кольца.
- 62. Потенциал заряженного отрезка прямой Найдём теперь
- 63. Потенциал отрезка
- 64. Преобразования.
- 65. Расчёт интеграла
- 66. Замена тригонометрических функций.
- 67. Преобразования формул.
- 68. Потенциал заряженного отрезка.
- 69. Потенциал над серединой отрезка
- 70. Потенциал над серединой отрезка
- 71. Предельные случаи.
- 72. Потенциал для бесконечного отрезка
- 73. Преобразование знаменателя.
- 74. Преобразование формул
- 75. Разность потенциалов в двух точках пространства около заряженной прямой.
- 76. Напряжённость поля заряженной прямой.
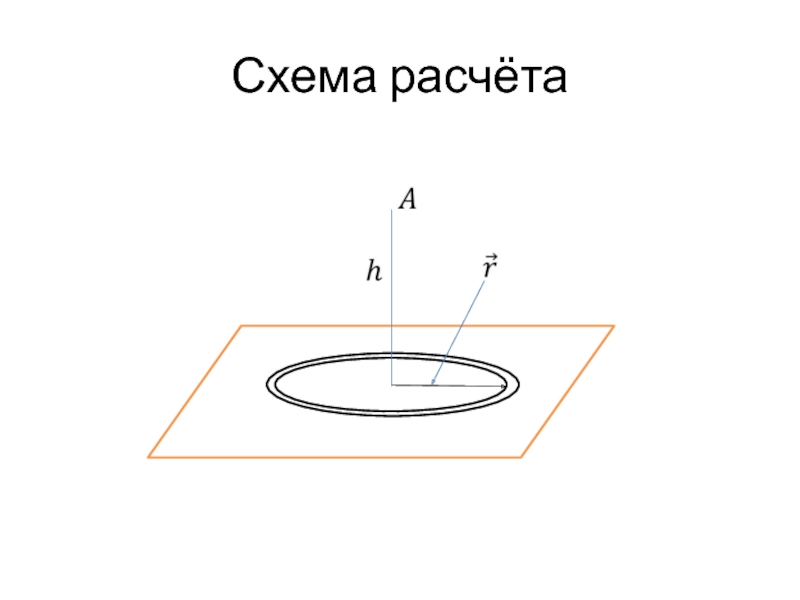
- 77. Заряженная плоскость.
- 78. Схема расчёта
- 79. Потенциал поля окружности
- 80. Элемент поля, создаваемого кольцом
- 81. Преобразование формул
- 82. Предельные случаи
- 83. Потенциал для бесконеченой плоскости
- 84. Разность потенциалов.
- 85. Напряжённость бесконечной плоскости.
Слайд 3Определение диполя.
Определение.
Система зарядов, состоящая из двух точечных равных и противоположных по
знаку зарядов, называется электрическим диполем. Вектор, идущий от отрицательного заряда к положительному, называется плечом диполя.
Слайд 201.5.Пондеромоторные силы.
Определение.
Пондеромоторными силами называются силы, действующие на тела со стороны различного
рода полей.
Рассмотрим силы действующие на электрические заряды в электрическом поле.
Рассмотрим силы действующие на электрические заряды в электрическом поле.
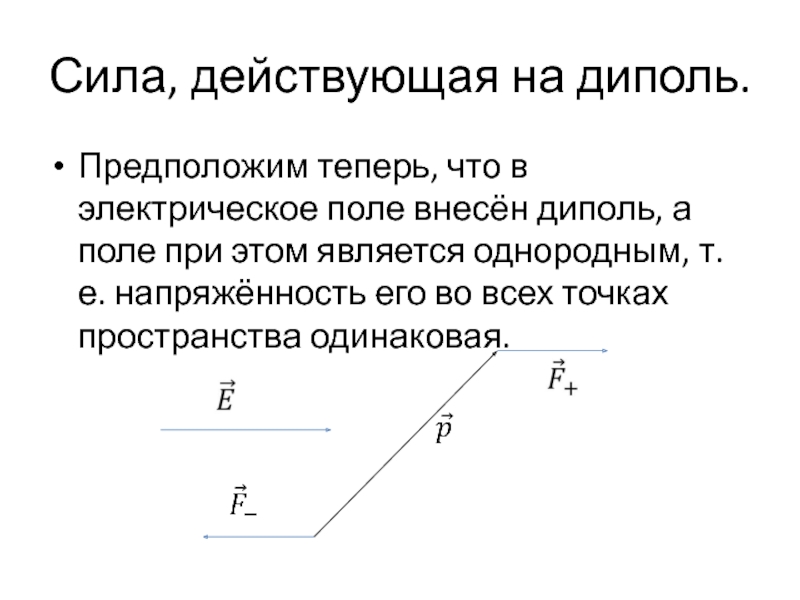
Слайд 23Сила, действующая на диполь.
Предположим теперь, что в электрическое поле внесён диполь,
а поле при этом является однородным, т.е. напряжённость его во всех точках пространства одинаковая.
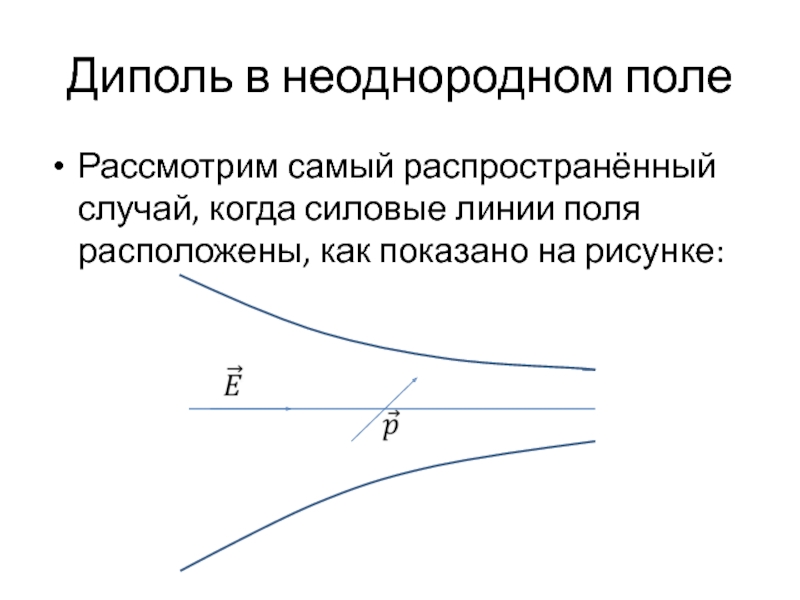
Слайд 38Диполь в неоднородном поле
Рассмотрим самый распространённый случай, когда силовые линии поля
расположены, как показано на рисунке:
Слайд 401.6.Прямой расчёт поля системы зарядов.
Часто система зарядов представляет собой не точечные
заряды, как у диполя, а непрерывное распределённые заряды. При этом в одной точке пространства зарядов может быть больше, в другой – меньше.
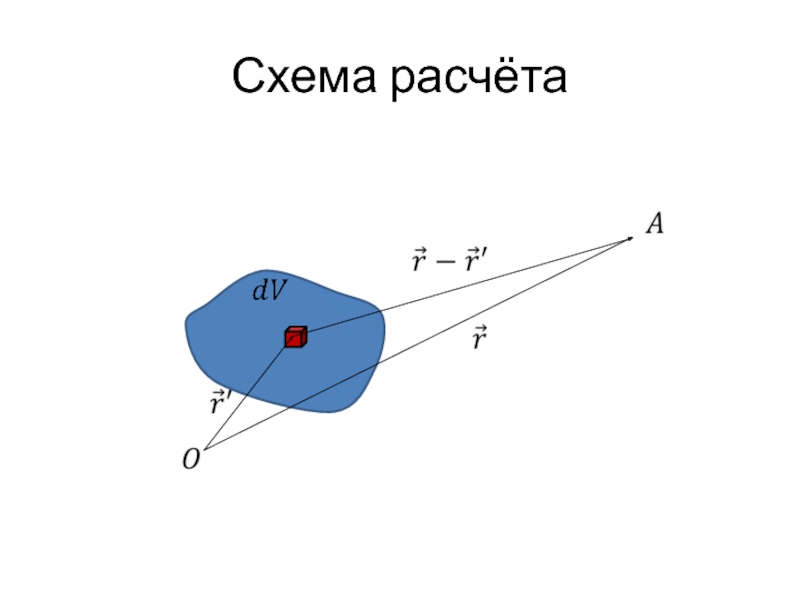
Слайд 41Объёмная плотность заряда.
Для характеристики распределения зарядов по пространству вводят понятие объёмной
плотности заряда.
Определение.
Объёмной плотностью заряда называется физическая величина, численно равная заряду единицы объёма.
Определение.
Объёмной плотностью заряда называется физическая величина, численно равная заряду единицы объёма.
Слайд 47Поверхностная система зарядов.
Расчёт поля с помощью прямого метода бывает сложным.
Иногда расчёт
упрощается, если система зарядов имеет специальную форму.
Например – поверхностная система зарядов.
Например – поверхностная система зарядов.
Слайд 48Поверхностная система зарядов
Определение.
Система зарядов, расположенная на некоторой поверхности, называется поверхностной системой
зарядов.
Слайд 52Линейная система зарядов
Определение.
Система зарядов, расположенных на некоторой кривой линии, называется линейной
системой зарядов.
Слайд 53Линейная плотность зарядов.
Определение.
Линейной плотностью заряда называется физическая величина, численно равная заряду
единицы длины кривой, на которой расположен заряд.
Слайд 62Потенциал заряженного отрезка прямой
Найдём теперь потенциал однородно заряженного отрезка прямой,
как показано на рисунке: