- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика – законы Ньютона презентация
Содержание
- 1. Динамика – законы Ньютона
- 2. К лекции 1- Эффект Доплера 1. Источник
- 3. К лекции 1- Эффект Доплера 1. Источник
- 4. К лекции 1- Эффект Доплера 1. Источник
- 5. К лекции 1- Эффект Доплера 1. Источник
- 6. К лекции 1- Эффект Доплера 1. Приемник
- 7. Эффект Доплера и принцип относительности Как мы
- 8. Динамика Динамика занимается изучением движения тел в связи с действующими на них силами.
- 9. Законы Динамики – редакция Ньютона Закон 1.
- 10. Первый закон Ньютона – Закон инерции Галилея
- 11. Галилео Галилей (1564 – 1642)
- 12. Галилео Галилей – Пизанский университет
- 13. Галилео Галилей-Пизанская башня
- 14. Галилей и инквизиция Утверждать, что Солнце стоит
- 15. Принцип относительности Галилея
- 16. Принцип относительности Галилея Инерциальные системы по своим
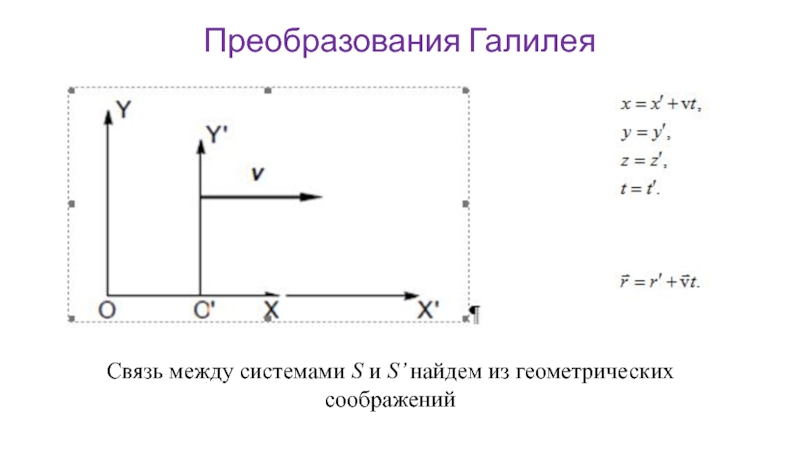
- 17. Преобразования Галилея Связь между системами S и S’ найдем из геометрических соображений
- 18. Преобразования Галилея Преобразование скорости Преобразование ускорения
- 19. Второй закон Ньютона- Масса Всякое тело оказывает
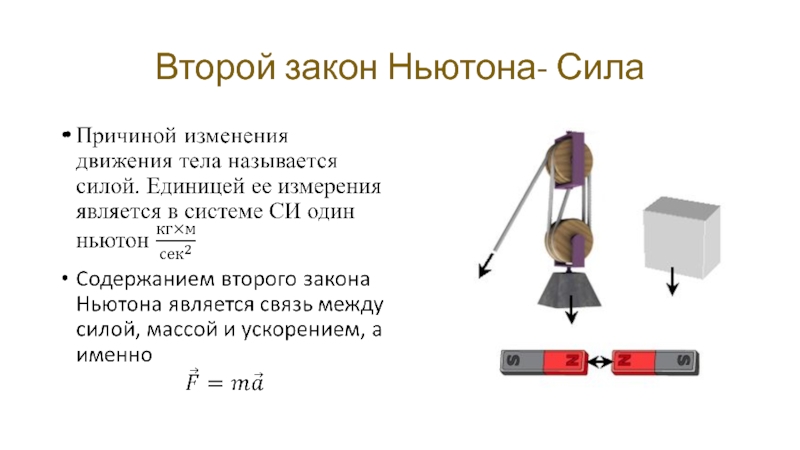
- 20. Второй закон Ньютона- Сила
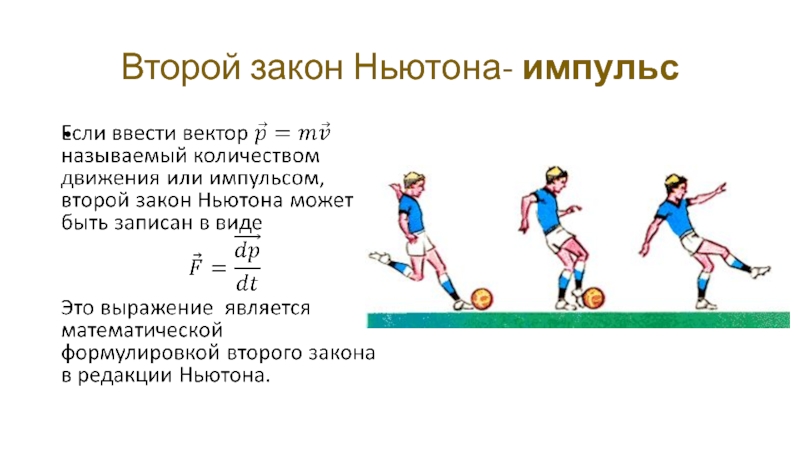
- 21. Второй закон Ньютона- импульс
- 22. Третий закон Ньютона
- 23. Силы - Виды взаимодействия
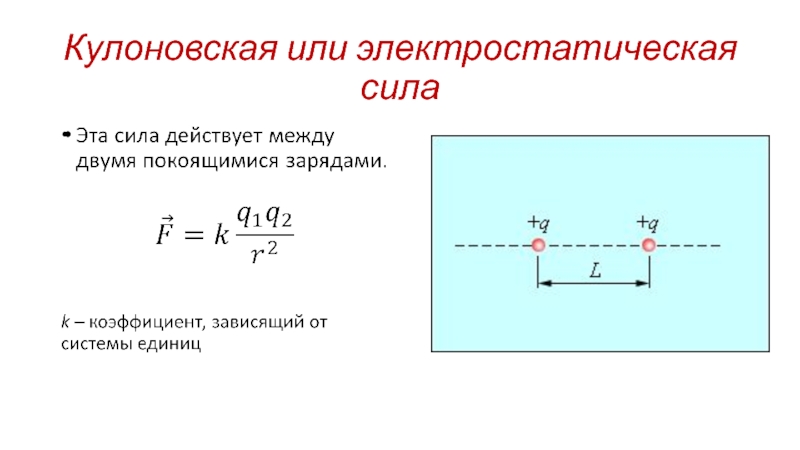
- 24. Кулоновская или электростатическая сила
- 25. Однородная сила тяжести
- 26. Упругая сила
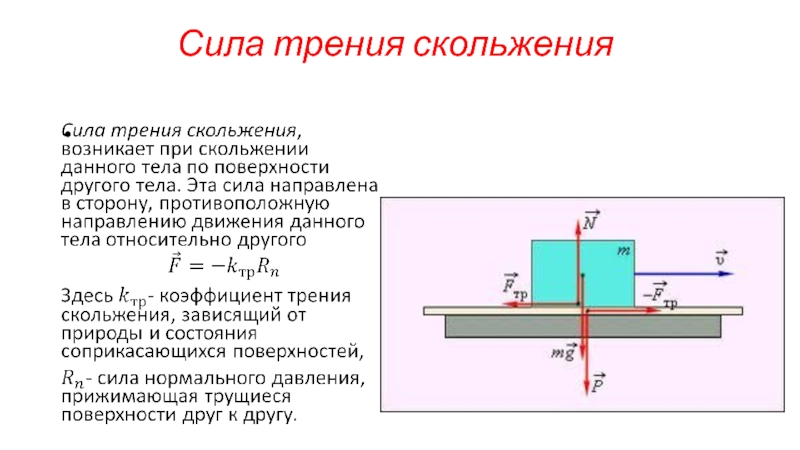
- 27. Сила трения скольжения
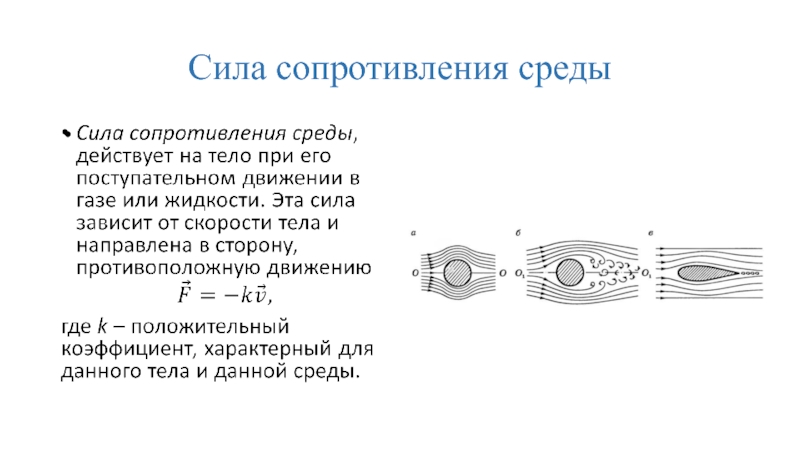
- 28. Сила сопротивления среды
- 29. Основное уравнение динамики Основное уравнение динамики
- 30. Основное уравнение динамики- Декартовы координаты Записывая обе
- 31. Декартовы координаты-пример Небольшой брусок массы т скользит
- 32. Декартовы координаты-пример Силы, действующие на брусок.
- 33. Декартовы координаты-пример Свяжем с системой отсчета «наклонная
- 34. Декартовы координаты-пример
- 35. Декартовы координаты-пример
- 36. Декартовы координаты-пример
- 37. Декартовы координаты-пример
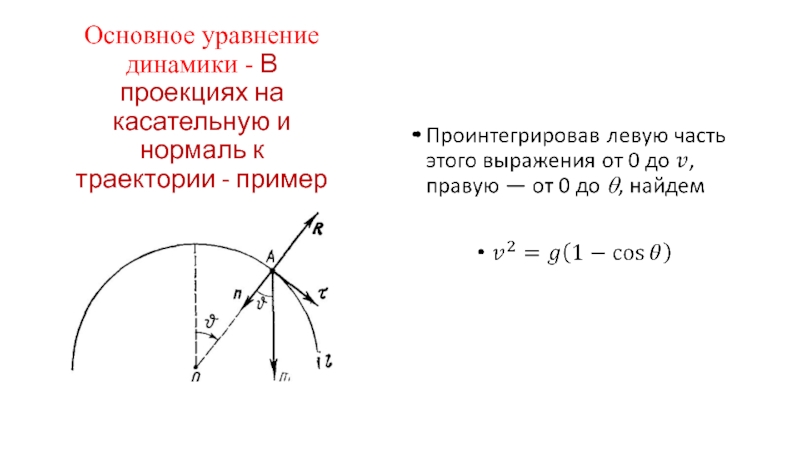
- 38. Основное уравнение динамики - В проекциях на
- 39. Основное уравнение динамики - В проекциях на
- 40. Основное уравнение динамики - В проекциях на
- 41. Основное уравнение динамики - В проекциях на
- 42. Основное уравнение динамики - В проекциях на
- 43. Основное уравнение динамики - В проекциях на
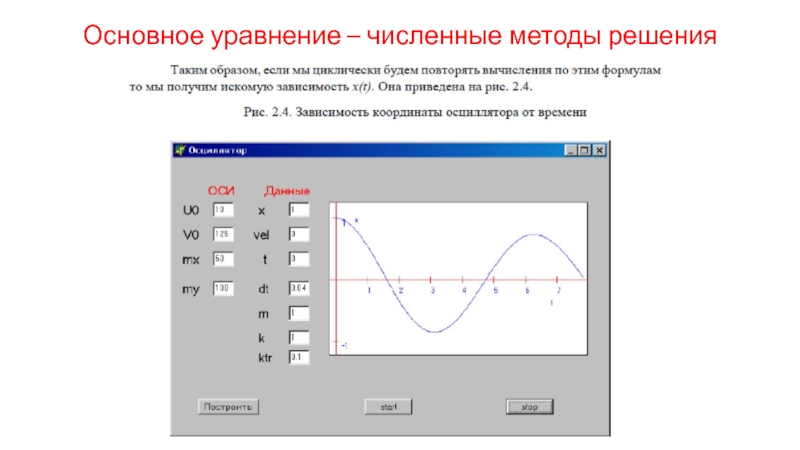
- 44. Основное уравнение – численные методы решения
- 45. Основное уравнение – численные методы решения
- 46. Основное уравнение – численные методы решения
- 47. Основное уравнение – численные методы решения
- 48. Основное уравнение – численные методы решения
- 49. Задача1
- 50. Задача 1.1
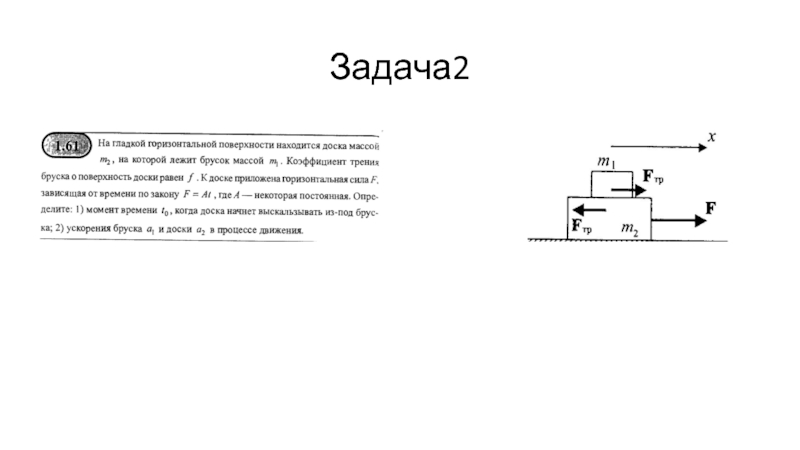
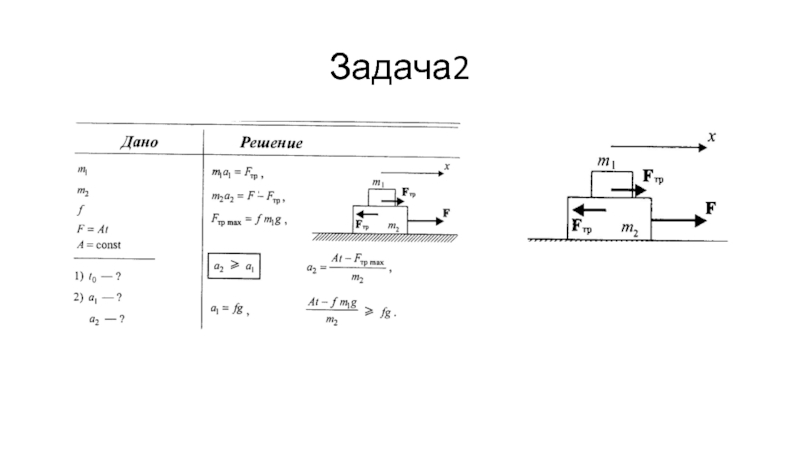
- 51. Задача2
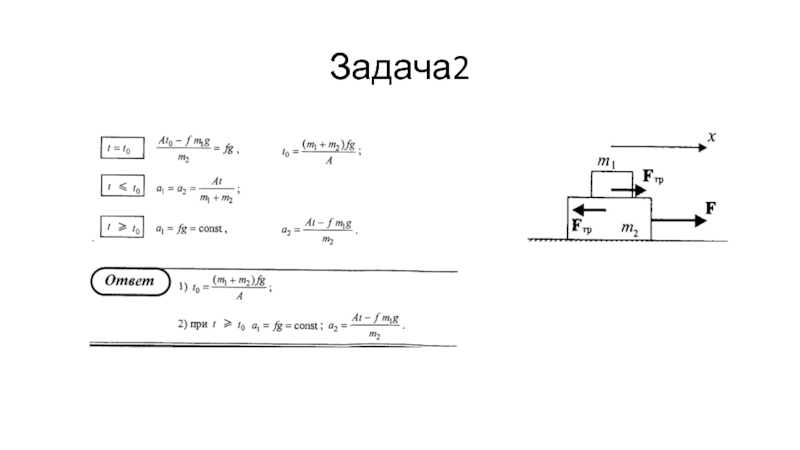
- 52. Задача2
- 53. Задача2
- 54. Задача 3
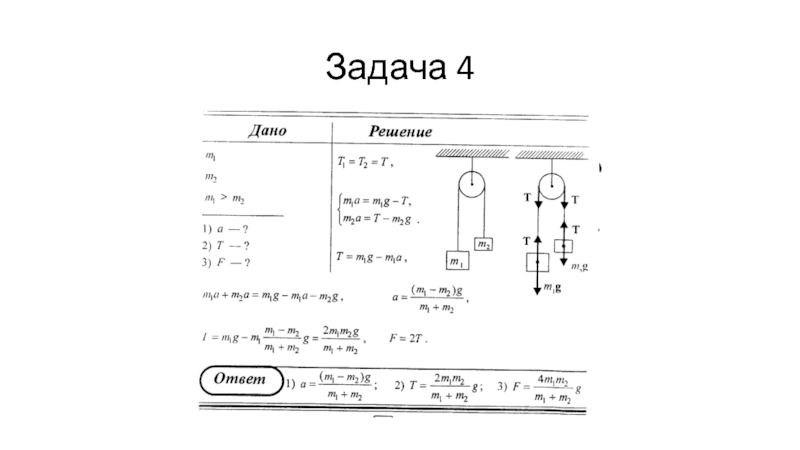
- 55. Задача 4
- 56. Задача 4
- 57. До следующей лекции
К лекции 1- Эффект Доплера
1. Источник движется, приемник остаётся неподвижным. Предположим, что источник, излучающий импульсы с периодом T, движется со скоростью v относительно среды по направлению к покоящемуся приемнику.
Слайд 2К лекции 1- Эффект Доплера
1. Источник движется, приемник остаётся неподвижным.
Предположим, что
источник, излучающий импульсы с периодом T, движется со скоростью
v относительно среды по направлению к покоящемуся приемнику.
В момент времени t=0 расстояние между источником и приемником равно L.
Первый импульс достигнет приемника в момент времени t=L/u, где u - скорость волны.
v относительно среды по направлению к покоящемуся приемнику.
В момент времени t=0 расстояние между источником и приемником равно L.
Первый импульс достигнет приемника в момент времени t=L/u, где u - скорость волны.
Слайд 3К лекции 1- Эффект Доплера
1. Источник движется, приемник остаётся неподвижным.
Второй импульс
будет послан к приемнику в момент времени t=T,
когда расстояние между источником и приемником равно L1=L-vT.
Таким образом, второй импульс достигнет приемника в момент времени t1=T+(L-vT)/u.
В результате, приемник будет регистрировать импульсы с периодом
Tдоп=t1-t= T(1- v/u)
когда расстояние между источником и приемником равно L1=L-vT.
Таким образом, второй импульс достигнет приемника в момент времени t1=T+(L-vT)/u.
В результате, приемник будет регистрировать импульсы с периодом
Tдоп=t1-t= T(1- v/u)
Слайд 4К лекции 1- Эффект Доплера
1. Источник движется, приемник остаётся неподвижным.
Таким образом,
частота сигнала fдоп, регистрируемого приемником, равна:
fдоп=f/(1-v/u) (источник движется навстречу приемнику)
где f - частота сигнала излучаемого источником.
Мы видим из этого выражения, что когда источник движется по направлению к приёмнику,
частота регистрируемого сигнала увеличивается на величину fv/u,
называемую доплеровским сдвигом частоты.
fдоп=f/(1-v/u) (источник движется навстречу приемнику)
где f - частота сигнала излучаемого источником.
Мы видим из этого выражения, что когда источник движется по направлению к приёмнику,
частота регистрируемого сигнала увеличивается на величину fv/u,
называемую доплеровским сдвигом частоты.
Слайд 5К лекции 1- Эффект Доплера
1. Источник движется, приемник остаётся неподвижным.
В случае
движущегося источника эффект Доплера возникает из-за того,
что изменяется длина волны, распространяющейся от источника к приемнику.
что изменяется длина волны, распространяющейся от источника к приемнику.
Слайд 6К лекции 1- Эффект Доплера
1. Приемник движется, источник остаётся
неподвижным.
Рассмотрим далее
случай, когда приемник движется, а источник волны неподвижен.
В этом случае длина волны не меняется и доплеровский сдвиг частоты возникает из-за того,
что изменяется скорость волны w относительно приемника:
w = u + v (приемник движется по направлению к источнику)
w = u - v (приемник движется по направлению от источника)
Так как fдоп=w/λ , а исходная частота источника f=u/λ0 и λ =λ0 мы получаем
fдоп=f(1+v/u) (приемник движется по направлению к источнику)
fдоп=f(1-v/u) (приемник движется по направлению от источника)
В этом случае длина волны не меняется и доплеровский сдвиг частоты возникает из-за того,
что изменяется скорость волны w относительно приемника:
w = u + v (приемник движется по направлению к источнику)
w = u - v (приемник движется по направлению от источника)
Так как fдоп=w/λ , а исходная частота источника f=u/λ0 и λ =λ0 мы получаем
fдоп=f(1+v/u) (приемник движется по направлению к источнику)
fдоп=f(1-v/u) (приемник движется по направлению от источника)
Слайд 7Эффект Доплера и принцип относительности
Как мы можем видеть из этих рассуждений,
сдвиг частоты будет разным в зависимости от того, что движется: приемник или источник. Особенно это заметно, если скорость источника или приемника близка к скорости волны. На первый взгляд может показаться что это противоречит принципу относительности: какая разница что движется - источник или приемник. На самом деле важно не относительное движение приемника и источника, а их движение относительно упругой среды, в которой распространяется волна. При этом скорость распространения волны не зависит от движения источника и приемника. В отличие от акустической волны для электромагнитной волны явления сдвига частоты протекают совершенно одинаково при движении источника и приемника.
Слайд 9Законы Динамики – редакция Ньютона
Закон 1. Всякое тело продолжает удерживаться в
своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Закон 2. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Закон 3. Действие всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.
Закон 2. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Закон 3. Действие всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.
Слайд 10Первый закон Ньютона – Закон инерции Галилея
Формулировка 1
Свободное тело, не подверженное
внешним воздействиям, либо находится в покое, либо движется равномерно и прямолинейно
Формулировка 2
Система отсчета, связанная со свободным телом называется инерциальной.
Инерциальные системы существуют
Слайд 14Галилей и инквизиция
Утверждать, что Солнце стоит неподвижно в центре мира — мнение
нелепое, ложное с философской точки зрения и формально еретическое, так как оно прямо противоречит Св. Писанию.
Утверждать, что Земля не находится в центре мира, что она не остаётся неподвижной и обладает даже суточным вращением, есть мнение столь же нелепое, ложное с философской и греховное с религиозной точки зрения.
Утверждать, что Земля не находится в центре мира, что она не остаётся неподвижной и обладает даже суточным вращением, есть мнение столь же нелепое, ложное с философской и греховное с религиозной точки зрения.
Слайд 16Принцип относительности Галилея
Инерциальные системы по своим механическим свойствам эквивалентны друг другу.
Никакими механическими опытами, проводимыми «внутри» данной инерциальной системы, нельзя установить, покоится эта система или движется.
Законы природы одинаковы во всех инерциальных системах.
Слайд 18Преобразования Галилея
Преобразование скорости
Преобразование ускорения
Длина вектора –
Инвариант преобразования
Галилея
Слайд 19Второй закон Ньютона- Масса
Всякое тело оказывает сопротивление при попытках привести его
в движение или изменить величину или направление его скорости. Это свойство тел называется инертностью. У разных тел оно проявляется в разной степени. Сообщить одно и то же ускорение большому камню значительно труднее, чем маленькому мячику. Мера инертности тела называется массой. Единицей массы в системе Си является килограмм, платино-иродиевый эталон которого хранится в палате мер и весов.
Слайд 29Основное уравнение динамики
Основное уравнение динамики представляет собой не что иное, как
математическое выражение второго закона Ньютона:
Слайд 30Основное уравнение динамики- Декартовы координаты
Записывая обе части уравнения в проекциях на
оси x,y,z получим три дифференциальных уравнения.
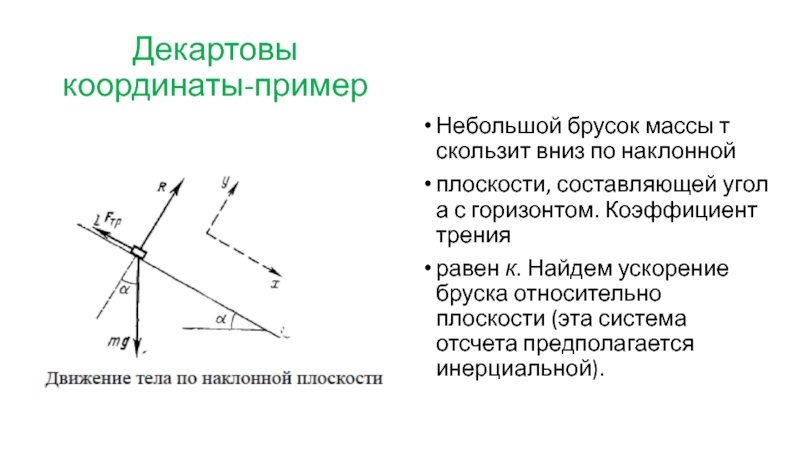
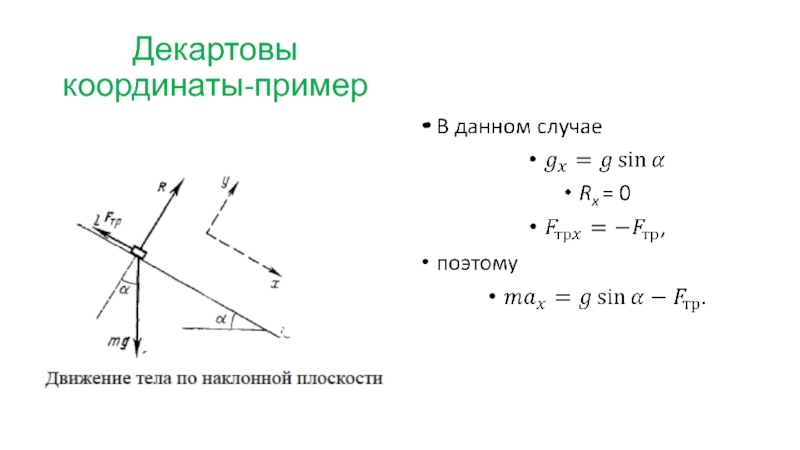
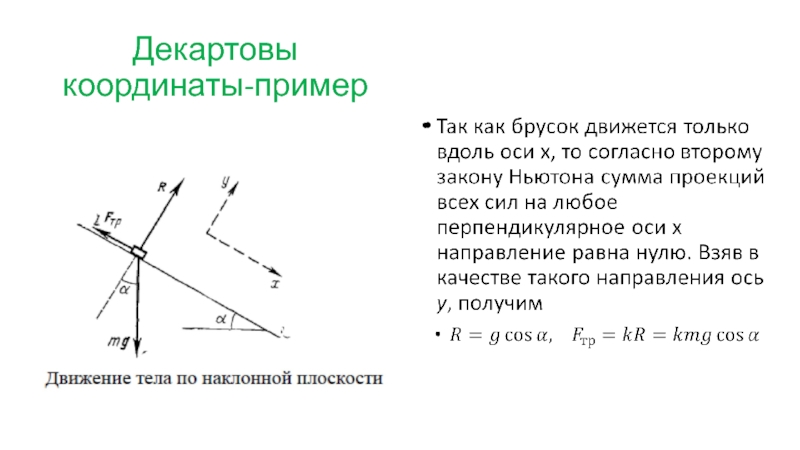
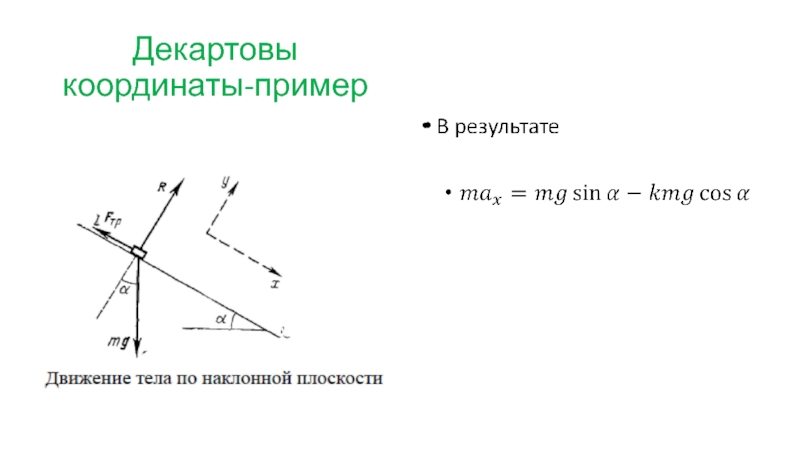
Слайд 31Декартовы координаты-пример
Небольшой брусок массы т скользит вниз по наклонной
плоскости, составляющей
угол а с горизонтом. Коэффициент трения
равен к. Найдем ускорение бруска относительно плоскости (эта система отсчета предполагается инерциальной).
равен к. Найдем ускорение бруска относительно плоскости (эта система отсчета предполагается инерциальной).
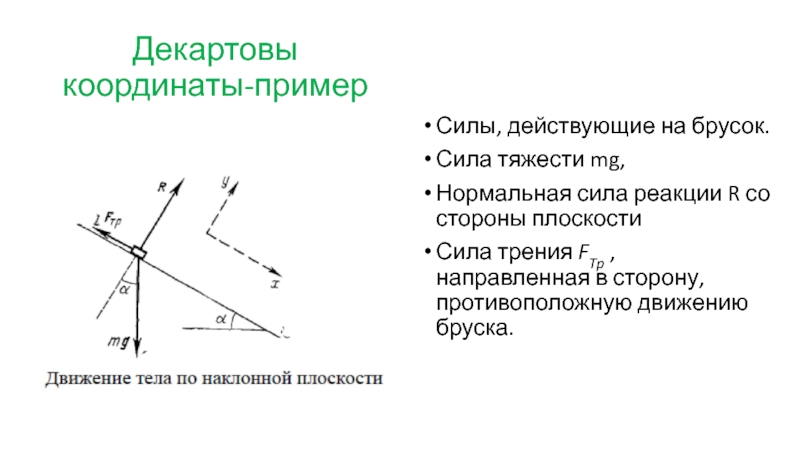
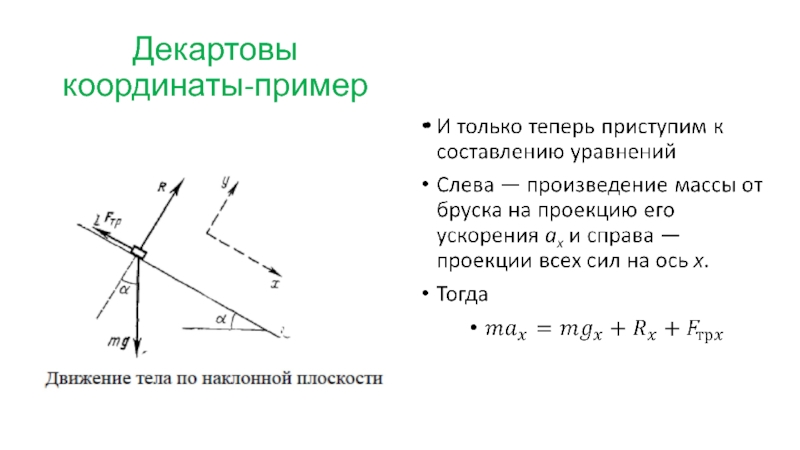
Слайд 32Декартовы координаты-пример
Силы, действующие на брусок.
Сила тяжести mg,
Нормальная сила реакции
R со стороны плоскости
Сила трения FTp , направленная в сторону, противоположную движению бруска.
Сила трения FTp , направленная в сторону, противоположную движению бруска.
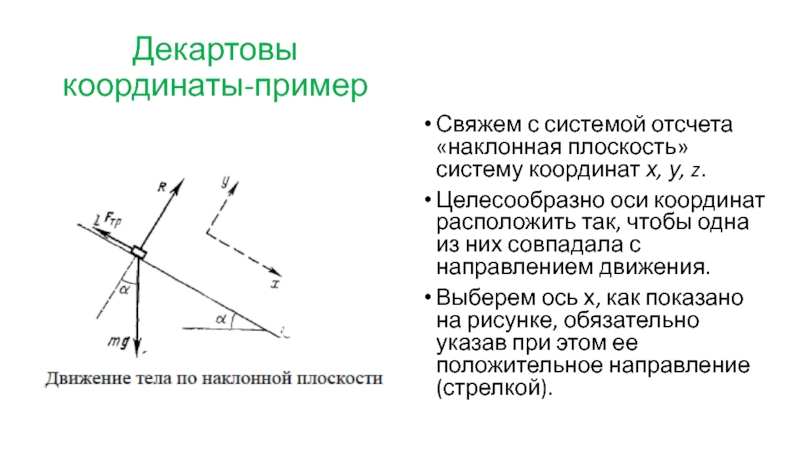
Слайд 33Декартовы координаты-пример
Свяжем с системой отсчета «наклонная плоскость» систему координат х, у,
z.
Целесообразно оси координат расположить так, чтобы одна из них совпадала с направлением движения.
Выберем ось х, как показано на рисунке, обязательно указав при этом ее положительное направление (стрелкой).
Целесообразно оси координат расположить так, чтобы одна из них совпадала с направлением движения.
Выберем ось х, как показано на рисунке, обязательно указав при этом ее положительное направление (стрелкой).
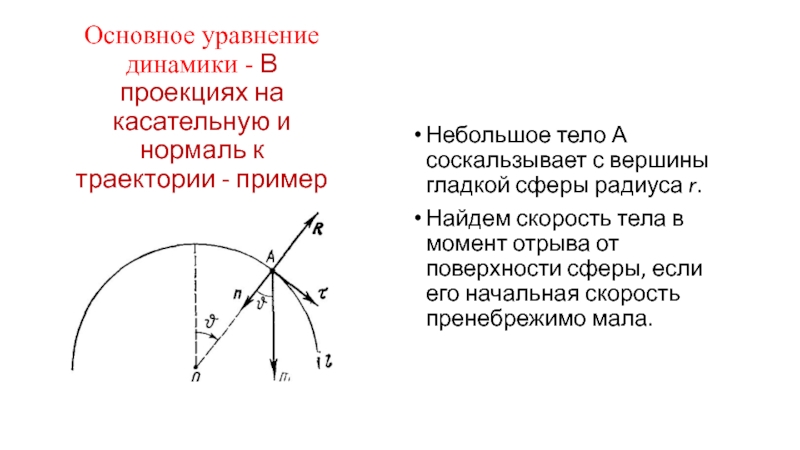
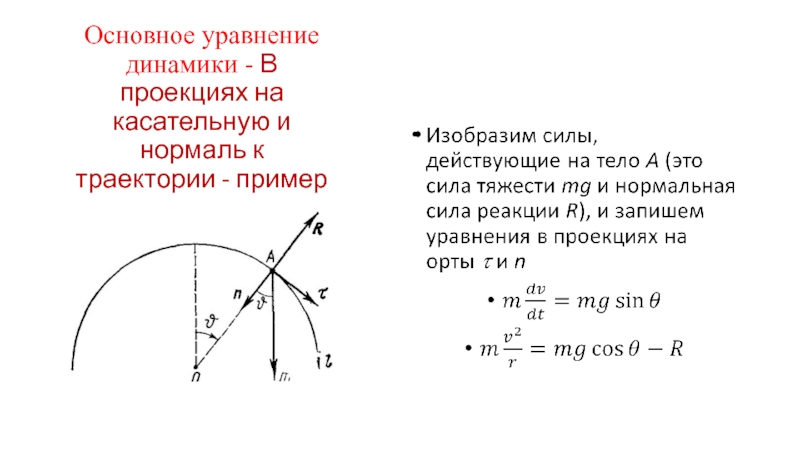
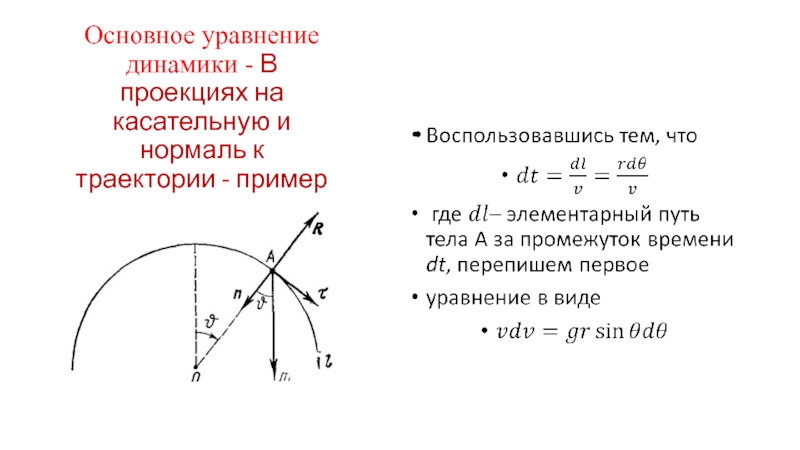
Слайд 39Основное уравнение динамики - В проекциях на касательную и нормаль к
траектории - пример
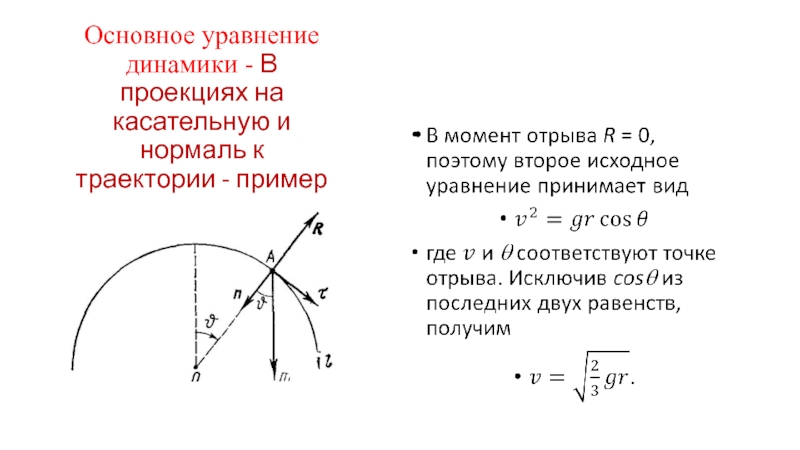
Небольшое тело А соскальзывает с вершины гладкой сферы радиуса r.
Найдем скорость тела в момент отрыва от поверхности сферы, если его начальная скорость пренебрежимо мала.
