- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика жидкости презентация
Содержание
- 1. Динамика жидкости
- 2. V. Динамика жидкости
- 4. Δm=ρΔV=ρΔlF=ρvΔtF ρ1 v1 Δt F1 = ρ2
- 5. уравнение неразрывности в гидравлической форме для элементарной
- 6. уравнение неразрывности для несжимаемой жидкости в дифференциальной
- 7. 2. Дифференциальные уравнения Эйлера для движения идеальной
- 8. разность давлений, действующих на противолежащие грани Разность сил в проекциях на оси координат будет
- 9. Тогда получим следующую систему уравнений Кроме сил
- 10. Дифференциальные уравнения Эйлера для движения идеальной жидкости.
- 11. 3. Уравнение Бернулли для идеальной жидкости Представим
- 12. При движение струйки установившегося потока под действием
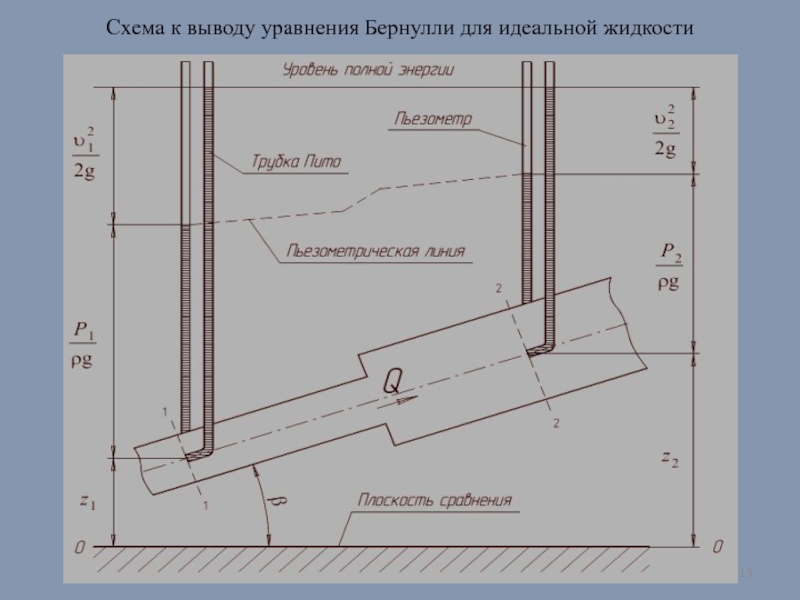
- 13. Схема к выводу уравнения Бернулли для идеальной жидкости
- 14. статический, или пьезометрический напор, равный давлению столба
- 15. Уравнение Бернулли для потока идеальной жидкости различные
- 16. При движении реальной жидкости hп -
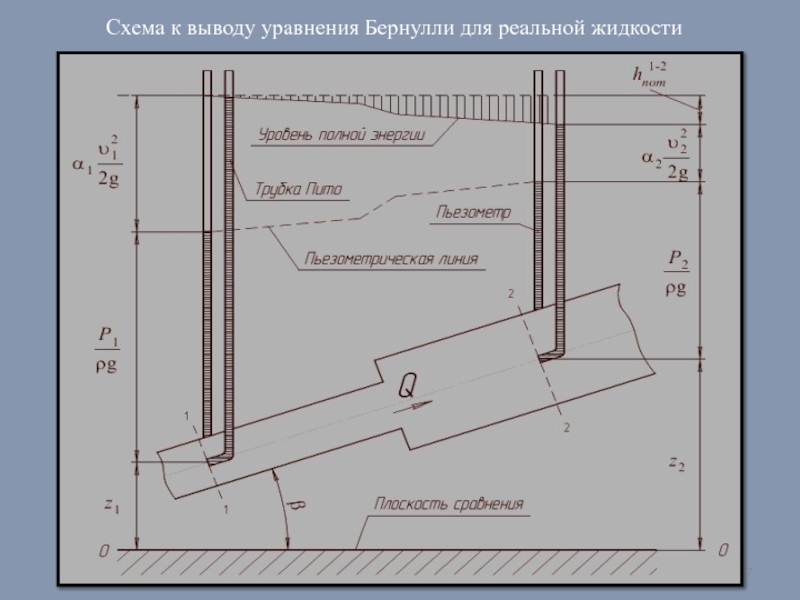
- 17. Схема к выводу уравнения Бернулли для реальной жидкости
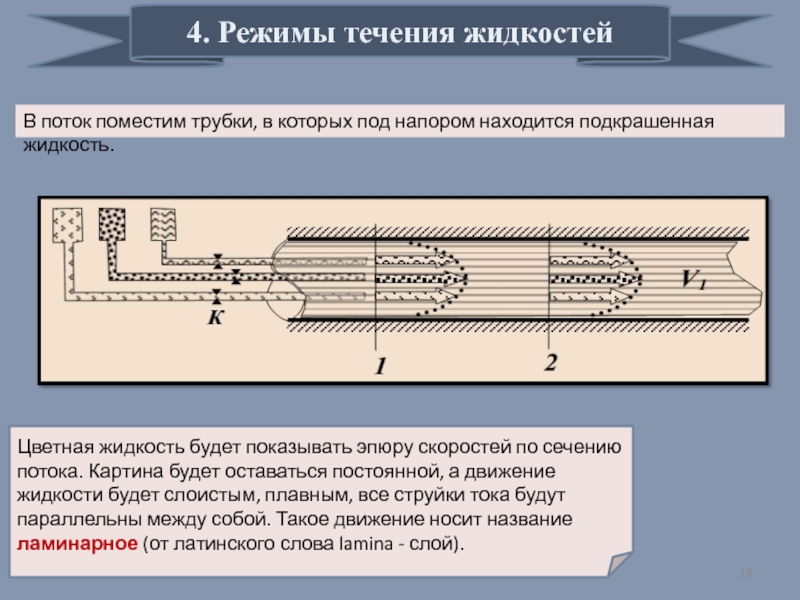
- 18. 4. Режимы течения жидкостей В поток поместим
- 19. Если увеличить скорость основного потока до величины
- 20. При дальнейшем увеличении скорости наступит такой момент,
- 21. Переход от одного режима движения к другому
- 22. 5. Гидравлические сопротивления в жидкости При движении
- 23. Потери напора h12 на преодоление сопротивлений
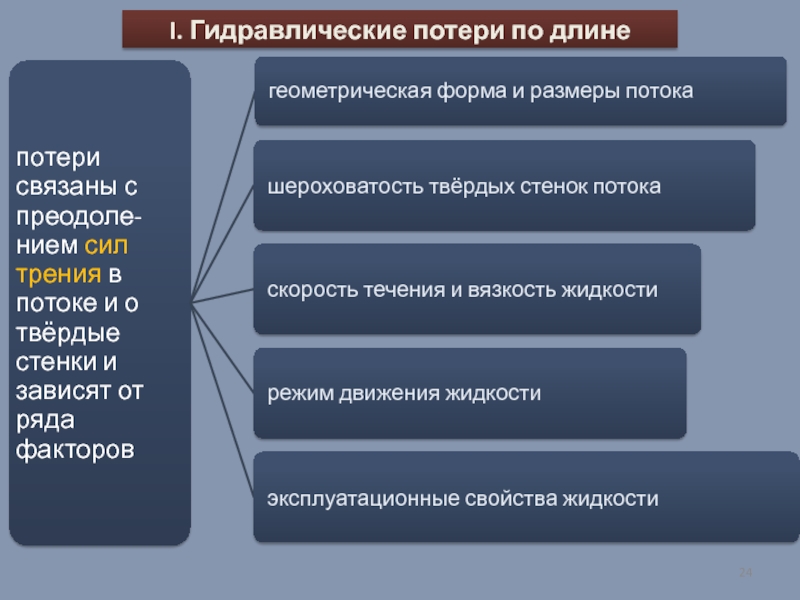
- 24. I. Гидравлические потери по длине
- 25. Возникают в прямых трубах с постоянным сечением
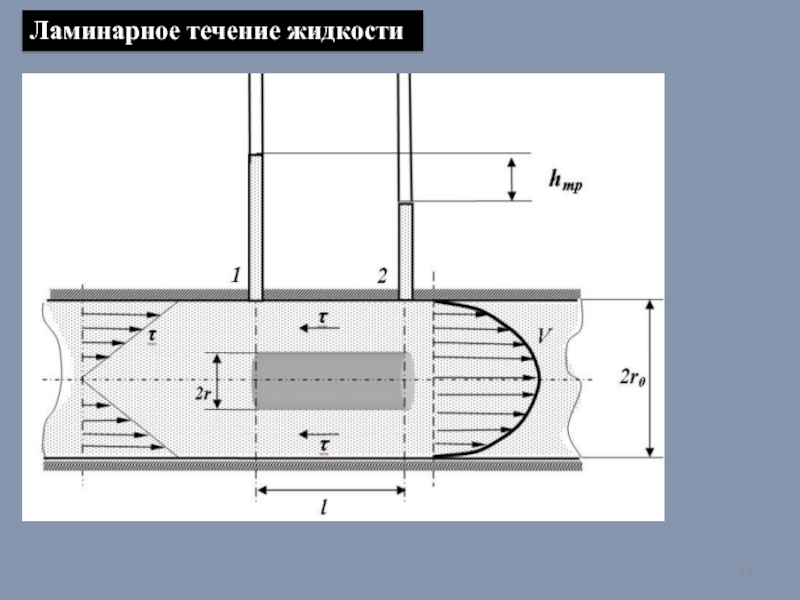
- 26. Ламинарное течение жидкости
- 28. Турбулентное течение жидкости Потери энергии (потери напора
- 29. Турбулентное ядро Турбулентное
- 31. цельнотянутые трубы из цветных металлов, трубы
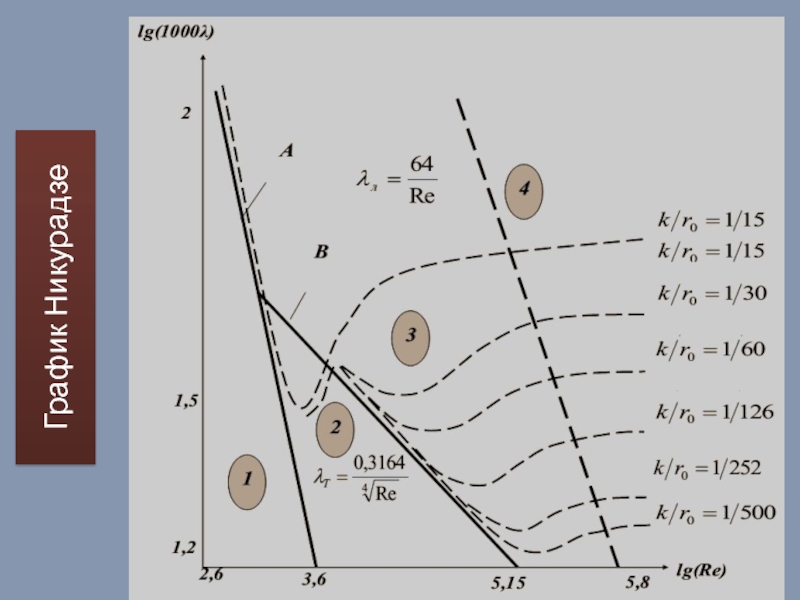
- 32. График Никурадзе
- 33. Выводы из графика Никурадзе
- 34. II. Местные гидравлические потери Местными гидравлическими сопротивлениями
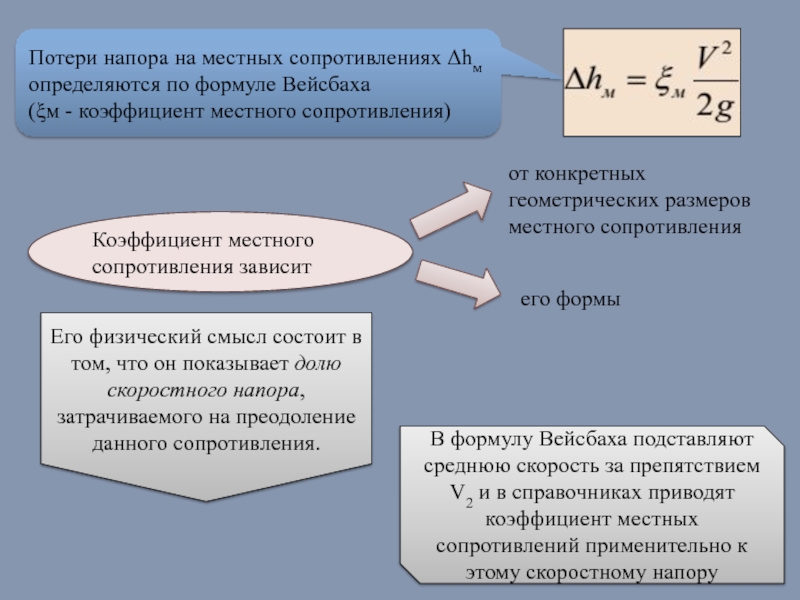
- 35. Потери напора на местных сопротивлениях Δhм определяются
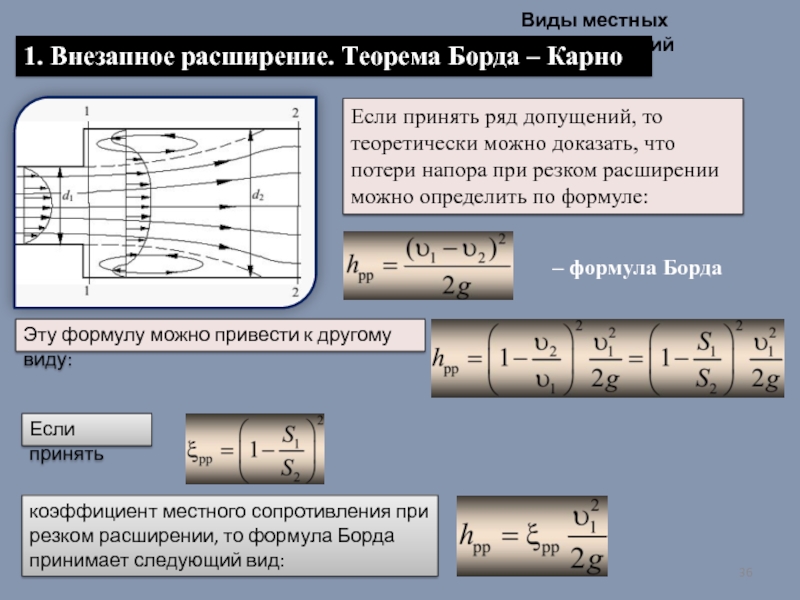
- 36. Виды местных сопротивлений 1. Внезапное расширение. Теорема
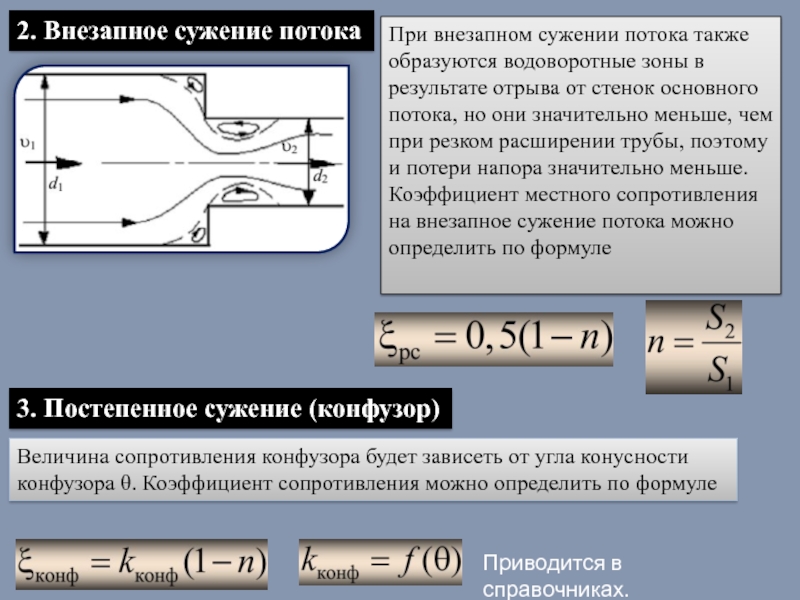
- 37. 2. Внезапное сужение потока При внезапном сужении
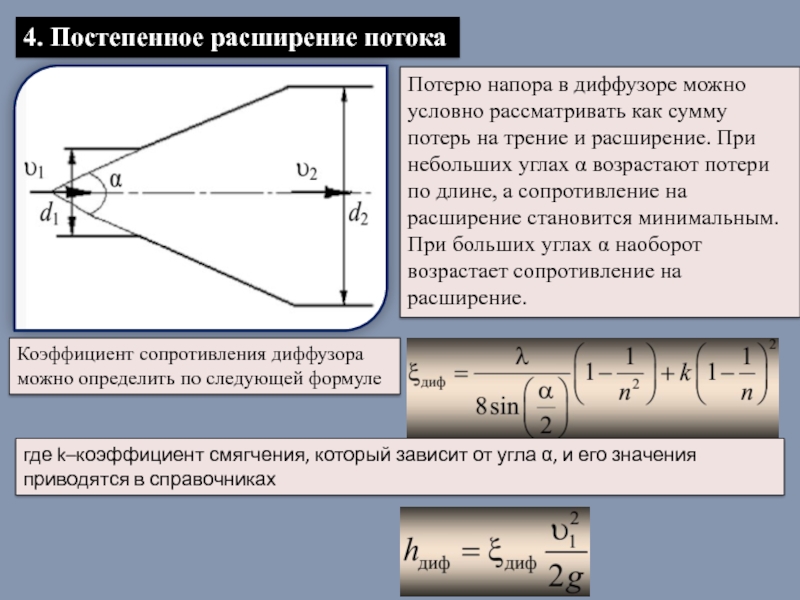
- 38. 4. Постепенное расширение потока Потерю напора в
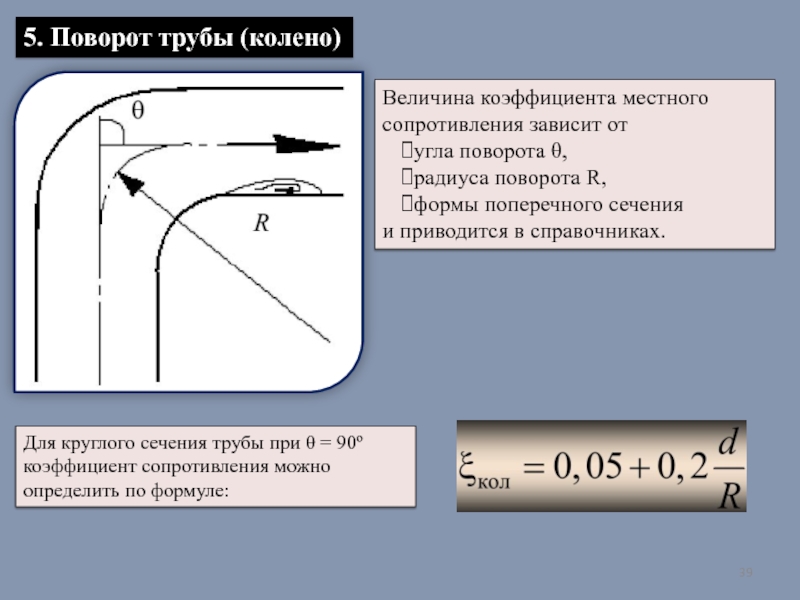
- 39. 5. Поворот трубы (колено) Величина коэффициента местного
- 40. 6. Другие виды местных сопротивлений Для ориентировочных
- 41. Кавитация На участках многих местных сопротивлений скорости
- 42. Кавитационные свойства местных сопротивлений оцениваются по критическому
Слайд 3
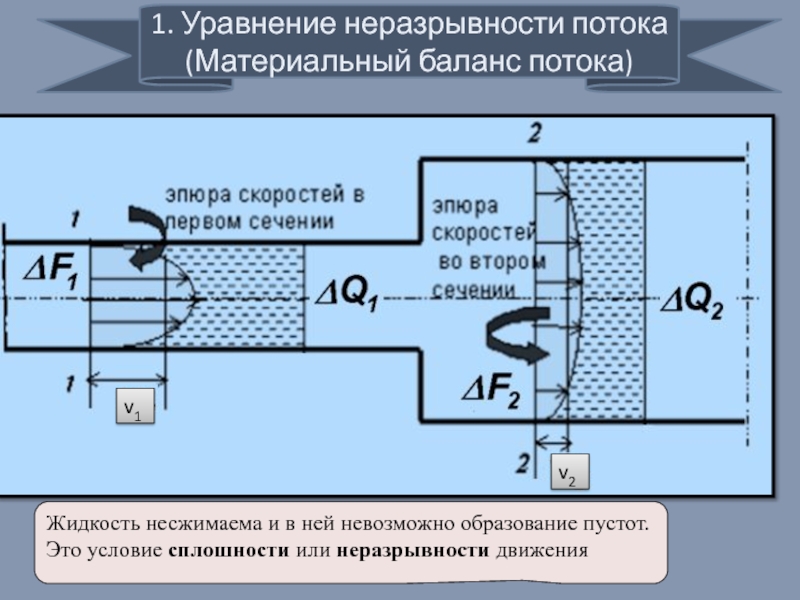
1. Уравнение неразрывности потока (Материальный баланс потока)
Жидкость несжимаема и в ней
v1
v2
Слайд 4Δm=ρΔV=ρΔlF=ρvΔtF
ρ1 v1 Δt F1 = ρ2 v2 Δt F2
v1 F1 =
скорость течения жидкости тем больше, чем уже поперечное сечение трубки; (она обратно пропорциональна площади поперечного сечения)
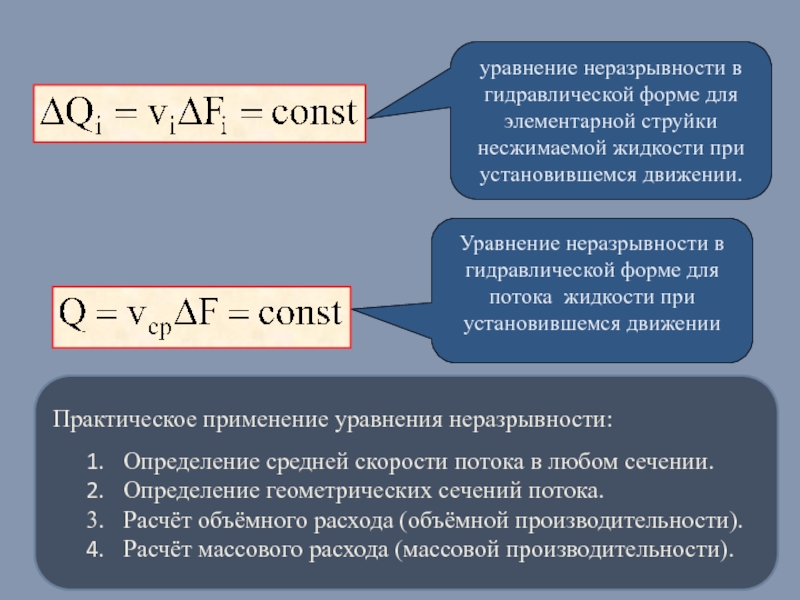
Слайд 5уравнение неразрывности в гидравлической форме для элементарной струйки несжимаемой жидкости при
установившемся движении.
Уравнение неразрывности в гидравлической форме для потока жидкости при установившемся движении
Практическое применение уравнения неразрывности:
Определение средней скорости потока в любом сечении.
Определение геометрических сечений потока.
Расчёт объёмного расхода (объёмной производительности).
Расчёт массового расхода (массовой производительности).
Слайд 6уравнение неразрывности для несжимаемой жидкости в дифференциальной форме
уравнение неразрывности для сжимаемой
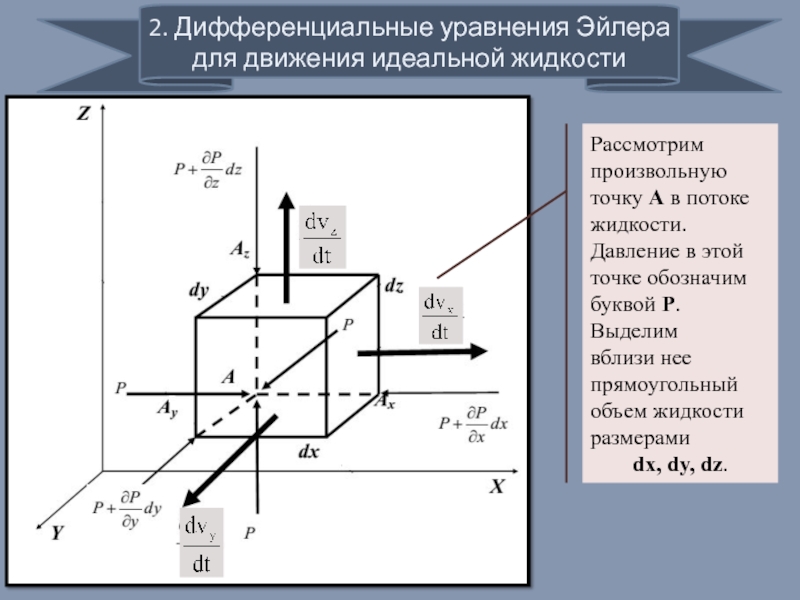
Слайд 72. Дифференциальные уравнения Эйлера для движения идеальной жидкости
Рассмотрим произвольную точку А
вблизи нее прямоугольный объем жидкости размерами
dx, dy, dz.
Слайд 8разность давлений, действующих на противолежащие грани
Разность сил в проекциях на оси
Слайд 9Тогда получим следующую систему уравнений
Кроме сил давления, на выделенный объём будут
Под действием этих сил рассматриваемый объём жидкости движется с ускорением
dv / dt,
или в проекциях на оси координат:
Слайд 10Дифференциальные уравнения Эйлера для движения идеальной жидкости.
(справедливы для движения без
Если уравнения Эйлера для движущейся жидкости дополнить проекциями сил вязкого трения на оси координат, получатся дифференциальные уравнения движения вязкой жидкости, которые носят название уравнения Навье-Стокса:
1
Слайд 113. Уравнение Бернулли для идеальной жидкости
Представим соответствующие проекции ускорений в уравнении
Умножим уравнения Эйлера соответственно на dx, dy и dz.
dP
dv2
уравнение Эйлера в преобразованном виде:
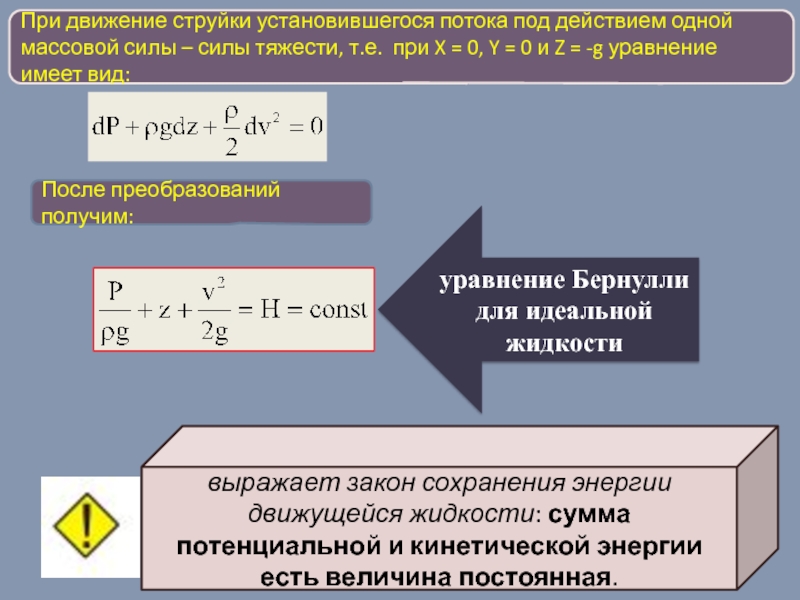
Слайд 12При движение струйки установившегося потока под действием одной массовой силы –
После преобразований получим:
уравнение Бернулли для идеальной жидкости
выражает закон сохранения энергии движущейся жидкости: сумма потенциальной и кинетической энергии есть величина постоянная.
Слайд 14статический, или пьезометрический напор, равный давлению столба жидкости над рассматриваемым уровнем,
нивелирная высота, или геометрический напор, который равен высоте расположения данного сечения над плоскостью сравнения. Выражает удельную потенциальную энергию положения точки
скоростной (динамический) напор, который выражает удельную кинетическую энергию в данной точке
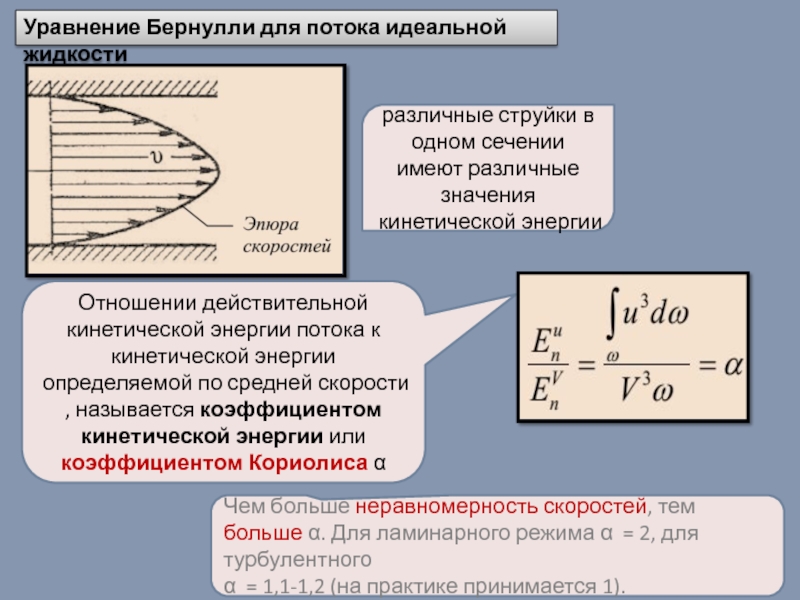
Слайд 15Уравнение Бернулли для потока идеальной жидкости
различные струйки в одном сечении имеют
Отношении действительной кинетической энергии потока к кинетической энергии определяемой по средней скорости , называется коэффициентом кинетической энергии или коэффициентом Кориолиса α
Чем больше неравномерность скоростей, тем больше α. Для ламинарного режима α = 2, для турбулентного
α = 1,1-1,2 (на практике принимается 1).
Слайд 16При движении реальной жидкости
hп - выражает потери напора на преодоление
гидравлических сопротивлений
Для движения реальной жидкости сумма статического и динамического напоров, нивелирной высоты и потерянного напора остаётся величиной постоянной и равна полному гидродинамическому напору Н.
Слайд 184. Режимы течения жидкостей
В поток поместим трубки, в которых под напором
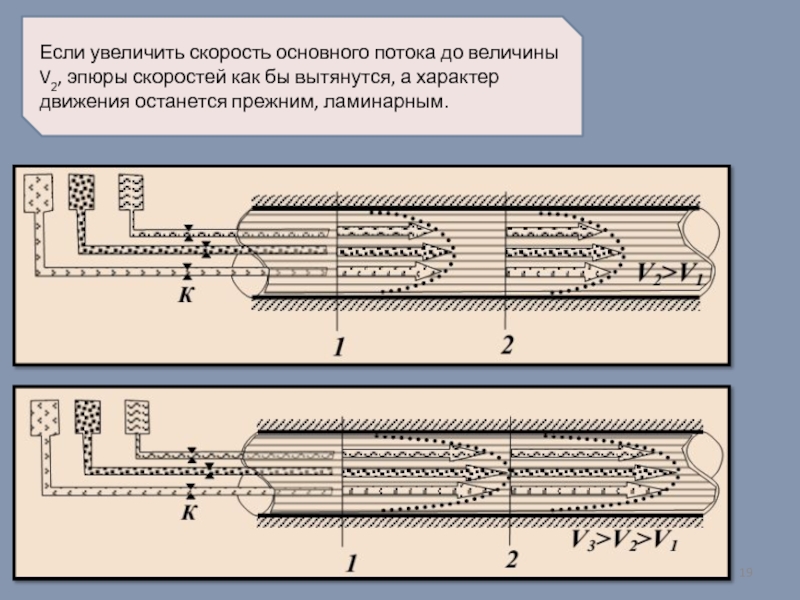
Цветная жидкость будет показывать эпюру скоростей по сечению потока. Картина будет оставаться постоянной, а движение жидкости будет слоистым, плавным, все струйки тока будут параллельны между собой. Такое движение носит название ламинарное (от латинского слова lamina - слой).
Слайд 19Если увеличить скорость основного потока до величины V2, эпюры скоростей как
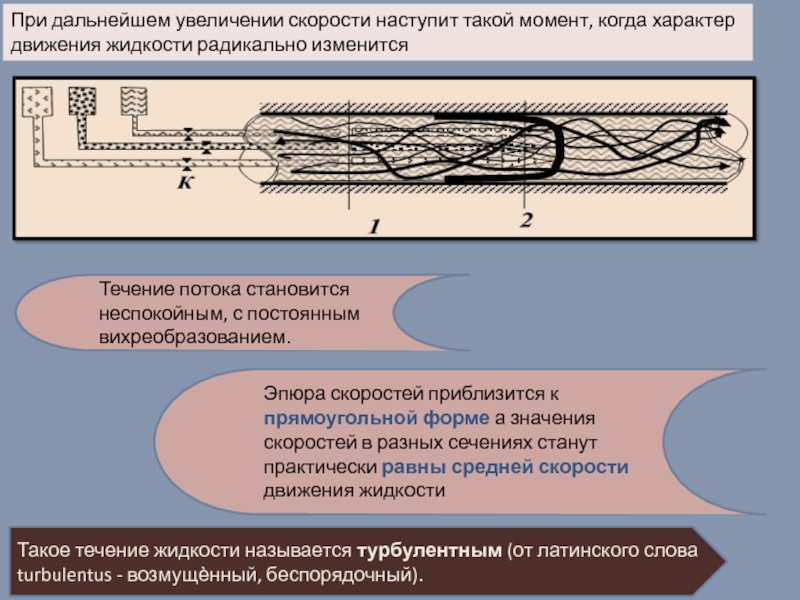
Слайд 20При дальнейшем увеличении скорости наступит такой момент, когда характер движения жидкости
Течение потока становится неспокойным, с постоянным вихреобразованием.
Эпюра скоростей приблизится к прямоугольной форме а значения скоростей в разных сечениях станут практически равны средней скорости движения жидкости
Такое течение жидкости называется турбулентным (от латинского слова turbulentus - возмущѐнный, беспорядочный).
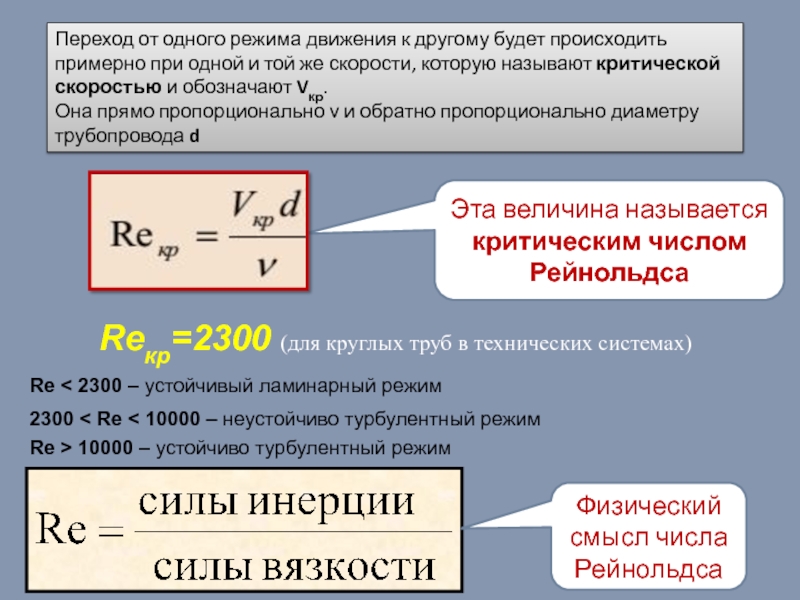
Слайд 21Переход от одного режима движения к другому будет происходить примерно при
Она прямо пропорционально ν и обратно пропорционально диаметру трубопровода d
Эта величина называется критическим числом Рейнольдса
Reкр=2300 (для круглых труб в технических системах)
Re < 2300 – устойчивый ламинарный режим
2300 < Re < 10000 – неустойчиво турбулентный режим
Re > 10000 – устойчиво турбулентный режим
Физический смысл числа Рейнольдса
Слайд 225. Гидравлические сопротивления в жидкости
При движении возникают сопротивления, на преодоление которых
Эту потерянную энергию называют гидравлическими потерями удельной энергии или потерями напора.
Потери энергии прямо пропорциональны квадрату скорости течения жидкости, поэтому в гидравлике принято выражать потерянную энергию в долях от кинетической энергии, отнесённой к единице веса жидкости
формула
Дарси–Вейсбаха:
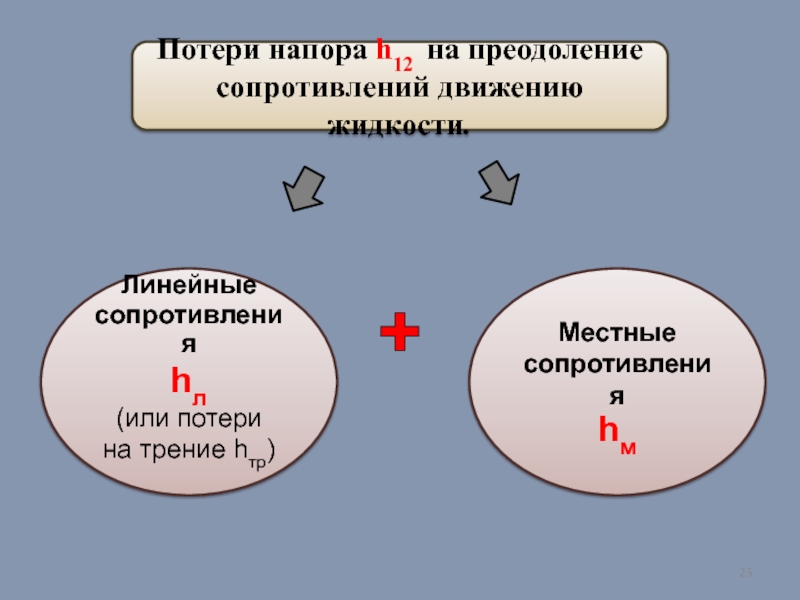
Слайд 23Потери напора h12 на преодоление
сопротивлений движению жидкости.
Линейные
сопротивления
hл
(или потери
на
Местные
сопротивления
hм
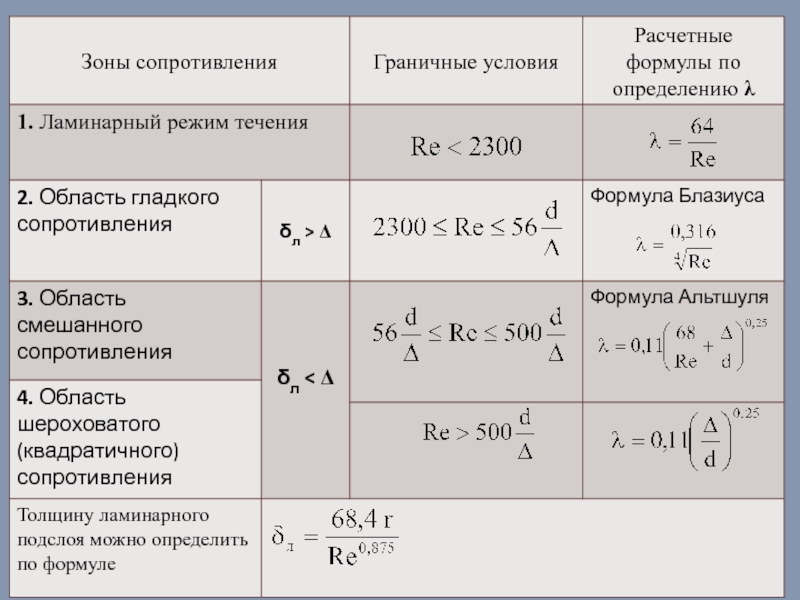
Слайд 25Возникают в прямых трубах с постоянным сечением при равномерном течении, обусловлены
где λ – коэффициент гидравлического трения
потери напора по длине выражаются формулой Дарси
Вспомним формулу Дарси-Вейсбаха:
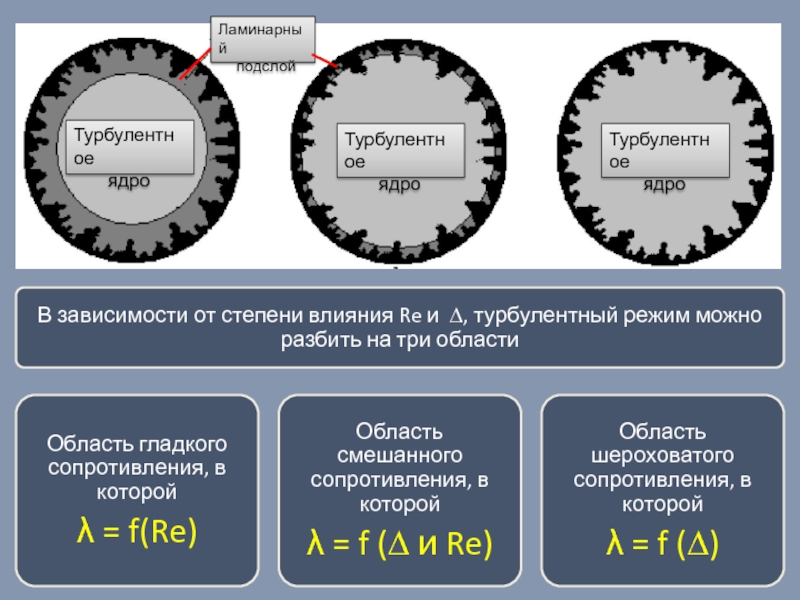
Слайд 28Турбулентное течение жидкости
Потери энергии (потери напора на трение) при турбулентном течении
турбулентный поток, как правило, не соприкасается со стенками трубы, а занимает только центральную часть (турбулентное ядро).
Между стенками трубы и турбулентным потоком существует тонкий слой жидкости, течение в котором является ламинарным (ламинарный подслой).
Слайд 31
цельнотянутые трубы из цветных металлов,
трубы из алюминиевых сплавов,
стальные высококачественные бесшовные трубы,
новые
новые не оцинкованные трубы
Технически гладкие трубы - шероховатость внутренних поверхностей настолько мала, что практически не влияет на потери энергии на трение
решающее значение имеет не абсолютная высота неровностей (абсолютная шероховатость) k, а отношение высоты этих неровностей к радиусу трубы r0. Эта величина обозначается k / r0 и называется относительной шероховатостью.
Слайд 34II. Местные гидравлические потери
Местными гидравлическими сопротивлениями называются любые участки гидравлической системы,
повороты,
преграды на пути потока рабочей жидкости,
расширения или сужения, вызывающие
внезапное изменение формы потока,
скорости или
направления ее движения.
В этих местах интенсивно теряется напор.
Слайд 35Потери напора на местных сопротивлениях Δhм определяются по формуле Вейсбаха
(ξм -
Коэффициент местного сопротивления зависит
от конкретных геометрических размеров местного сопротивления
его формы
Его физический смысл состоит в том, что он показывает долю скоростного напора, затрачиваемого на преодоление данного сопротивления.
В формулу Вейсбаха подставляют среднюю скорость за препятствием V2 и в справочниках приводят коэффициент местных сопротивлений применительно к этому скоростному напору
Слайд 36Виды местных сопротивлений
1. Внезапное расширение. Теорема Борда – Карно
Если принять ряд
– формула Борда
Эту формулу можно привести к другому виду:
Если принять
коэффициент местного сопротивления при резком расширении, то формула Борда принимает следующий вид:
Слайд 372. Внезапное сужение потока
При внезапном сужении потока также образуются водоворотные зоны
Коэффициент местного сопротивления на внезапное сужение потока можно определить по формуле
Величина сопротивления конфузора будет зависеть от угла конусности конфузора θ. Коэффициент сопротивления можно определить по формуле
3. Постепенное сужение (конфузор)
Приводится в справочниках.
Слайд 384. Постепенное расширение потока
Потерю напора в диффузоре можно условно рассматривать как
При больших углах α наоборот возрастает сопротивление на
расширение.
где k–коэффициент смягчения, который зависит от угла α, и его значения приводятся в справочниках
Коэффициент сопротивления диффузора можно определить по следующей формуле
Слайд 395. Поворот трубы (колено)
Величина коэффициента местного
сопротивления зависит от
угла поворота θ,
радиуса поворота R,
формы поперечного сечения
и приводится в справочниках.
Для круглого сечения трубы при θ = 90º коэффициент сопротивления можно определить по формуле:
Слайд 406. Другие виды местных сопротивлений
Для ориентировочных расчетов можно пользоваться следующими коэффициентами
задвижка при полном открытии – 0,15;
вход в трубу при острых кромках – 0,5;
вентиль с косым затвором при полном открытии – 3;
симметричный тройник – 1,5.
Слайд 41Кавитация
На участках многих местных сопротивлений скорости потока резко возрастают, в результате
Источником кавитации являются пузырьки газа и пара, которые выделяются в сечении с пониженным давлением. Попадая в сечение с нормальным давлением, пузырьки мгновенно исчезают под действием повышенного давления. В месте исчезновения пузырьков давление резко увеличивается, повышается температура
Кавитация неблагоприятно отражается на работе
оборудования, т.к. возникает
вибрация,
шум,
эрозия металла.
Слайд 42Кавитационные свойства местных сопротивлений оцениваются по критическому значению числа кавитации:
– давление
где
Предельно допустимая скорость в трубопроводе перед местным сопротивлением определяют по формуле
Необходимо выполнение условия