- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика вращательного движения. (Тема 4) презентация
Содержание
- 1. Динамика вращательного движения. (Тема 4)
- 2. 1. ДВИЖЕНИЕ ЦЕНТРА МАСС ТВЕРДОГО ТЕЛА Центр
- 3. 2. МОМЕНТ ИМПУЛЬСА ЧАСТИЦЫ ОТНОСИТЕЛЬНО ТОЧКИ Моментом
- 4. 3.МОМЕНТ ИМПУЛЬСА ЧАСТИЦЫ ОТНОСИТЕЛЬНО ОСИ Проекция вектора
- 5. 4. СВОЙСТВА МОМЕНТ ИМПУЛЬСА 1. Псевдовектор.
- 6. 4. СВОЙСТВА МОМЕНТ ИМПУЛЬСА 1. Псевдовектор.
- 7. 5. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ Моментом
- 8. 6. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ Проекция
- 9. 7. КОМПОНЕНТЫ МОМЕНТА СИЛЫ Вклад в Mz
- 10. 8. УРАВНЕНИЕ МОМЕНТОВ (I) Запишем уравнение
- 11. 8. УРАВНЕНИЕ МОМЕНТОВ (II) Мы доказали,
- 12. 9. УРАВНЕНИЕ МОМЕНТОВ ДЛЯ СИСТЕМЫ ЧАСТИЦ
- 13. 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Момент импульса замкнутой (изолированной) системы есть величина постоянная.
- 14. 11. МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА
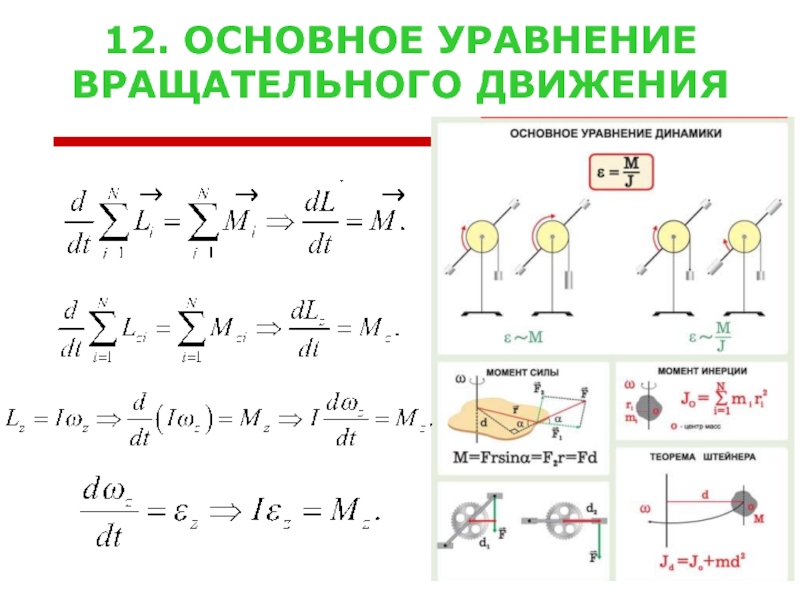
- 15. 12. ОСНОВНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- 16. 13. МОМЕНТ ИМПУЛЬСА И МОМЕНТ ИНЕРЦИИ
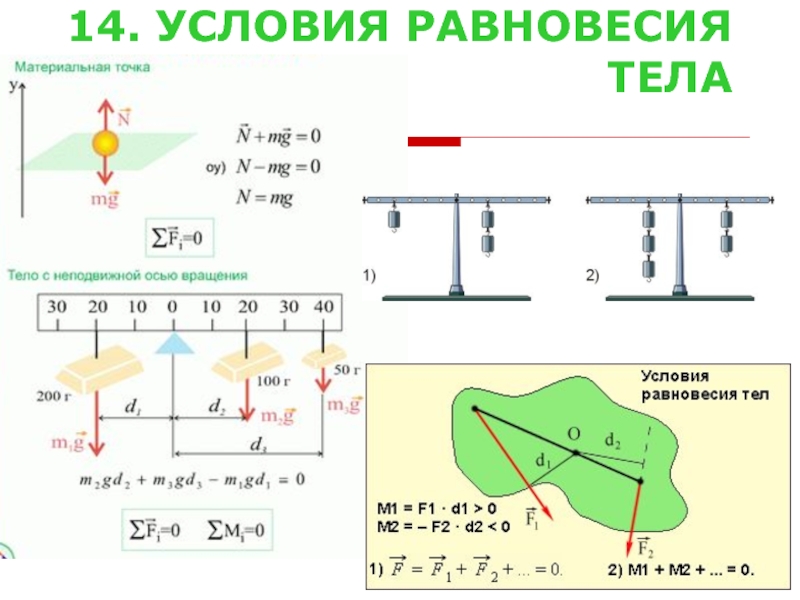
- 17. 14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА
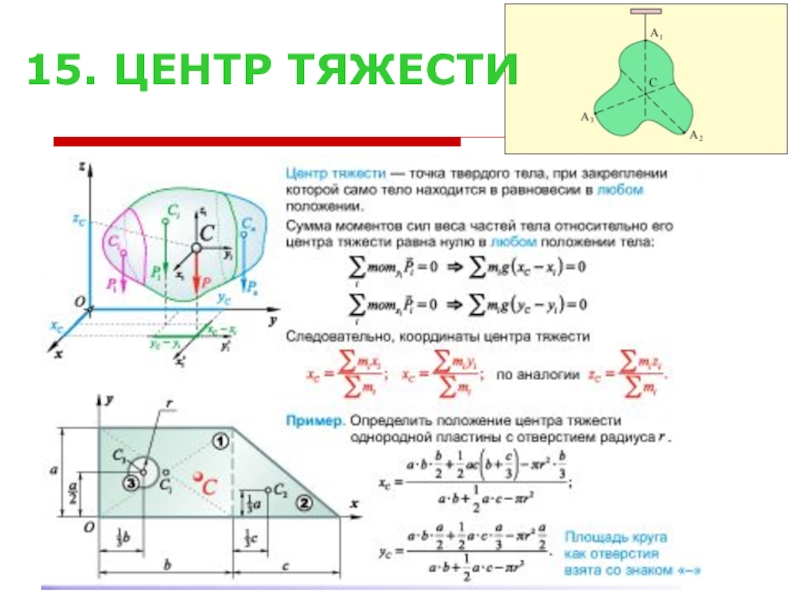
- 18. 15. ЦЕНТР ТЯЖЕСТИ
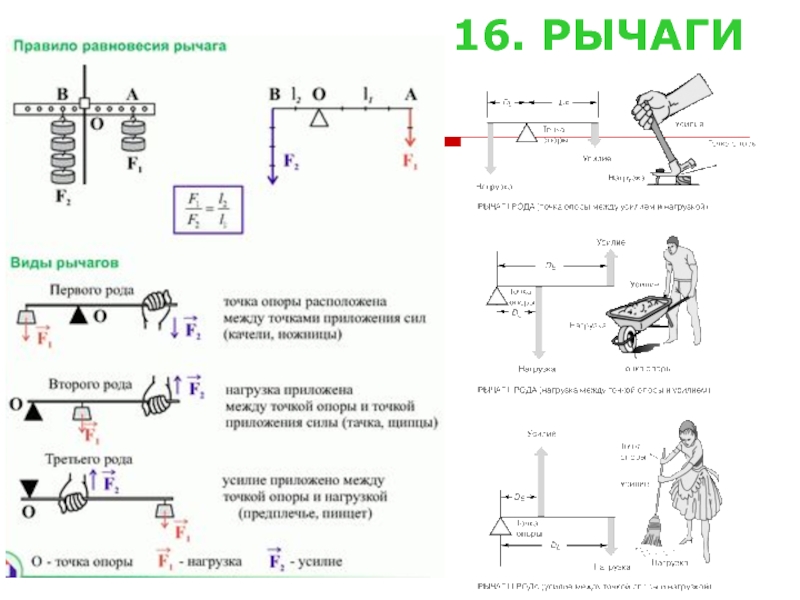
- 19. 16. РЫЧАГИ
Слайд 21. ДВИЖЕНИЕ ЦЕНТРА МАСС
ТВЕРДОГО ТЕЛА
Центр масс твердого тела движется так, как
материальная точка с массой, равной массе тела,
под действием всех приложенных к телу (внешних) сил.
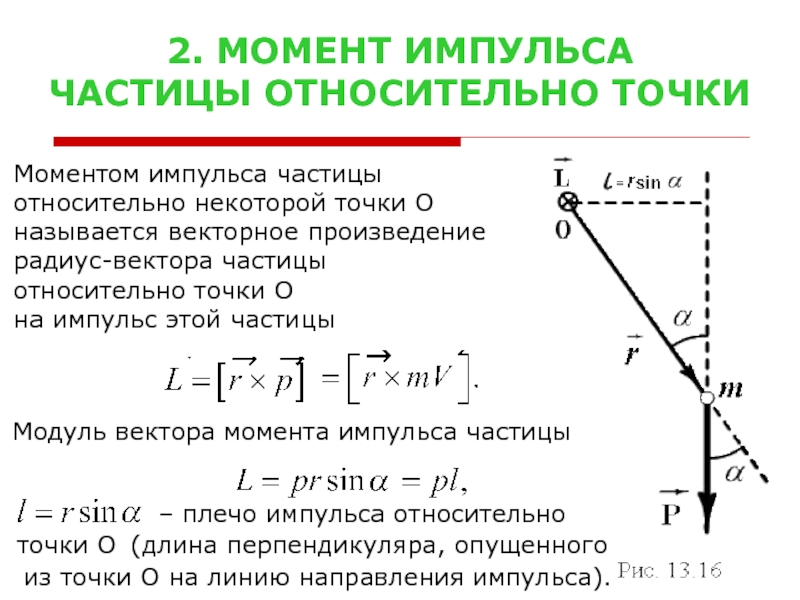
Слайд 32. МОМЕНТ ИМПУЛЬСА
ЧАСТИЦЫ ОТНОСИТЕЛЬНО ТОЧКИ
Моментом импульса частицы
относительно некоторой точки О
называется
радиус-вектора частицы
относительно точки О
на импульс этой частицы
Модуль вектора момента импульса частицы
– плечо импульса относительно
точки О
(длина перпендикуляра, опущенного
из точки О на линию направления импульса).
Слайд 43.МОМЕНТ ИМПУЛЬСА
ЧАСТИЦЫ ОТНОСИТЕЛЬНО ОСИ
Проекция вектора
момента импульса частицы
на некоторую ось
моментом импульса частицы
относительно этой оси
– угол между
и
– угол между
и осью z.
Момент импульса частицы относительно точки – вектор,
момент импульса частицы относительно оси – скаляр.
Моментом импульса системы частиц
относительно оси z называется величина
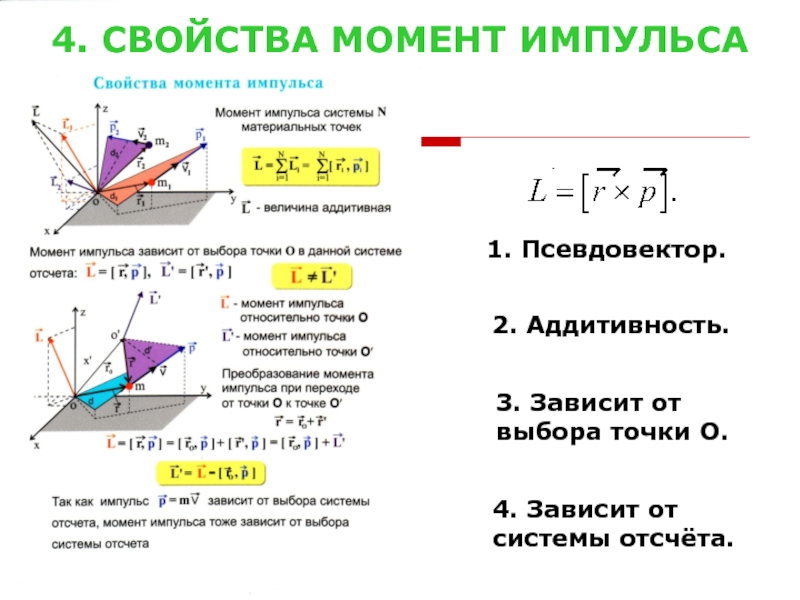
Слайд 54. СВОЙСТВА МОМЕНТ
ИМПУЛЬСА
1. Псевдовектор.
2. Аддитивность.
3. Зависит от
выбора точки
4. Зависит от
системы отсчёта.
Направление момента импульса определяется
правилом
Слайд 64. СВОЙСТВА МОМЕНТ ИМПУЛЬСА
1. Псевдовектор.
2. Аддитивность.
3. Зависит от
выбора точки
4. Зависит от
системы отсчёта.
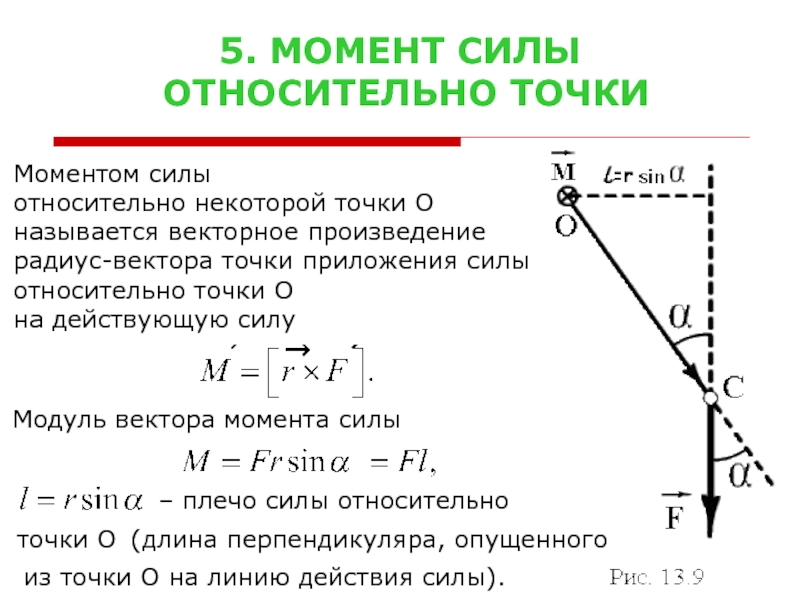
Слайд 75. МОМЕНТ СИЛЫ
ОТНОСИТЕЛЬНО ТОЧКИ
Моментом силы
относительно некоторой точки О
называется
радиус-вектора точки приложения силы
относительно точки О
на действующую силу
Модуль вектора момента силы
– плечо силы относительно
точки О
(длина перпендикуляра, опущенного
из точки О на линию действия силы).
Слайд 86. МОМЕНТ СИЛЫ
ОТНОСИТЕЛЬНО ОСИ
Проекция вектора
момента силы
на некоторую ось
моментом силы
относительно этой оси
– угол между
и
– угол между
и осью z.
Слайд 97. КОМПОНЕНТЫ МОМЕНТА СИЛЫ
Вклад в Mz даёт только
компонент силы,
перпендикулярный
плоскости рисунка.
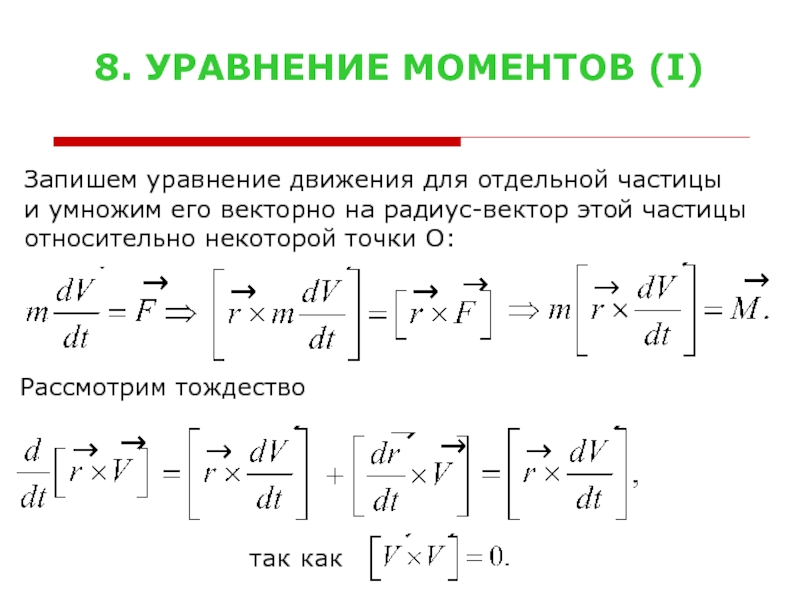
Слайд 108. УРАВНЕНИЕ МОМЕНТОВ (I)
Запишем уравнение движения для отдельной частицы
и
относительно некоторой точки О:
Рассмотрим тождество
так как
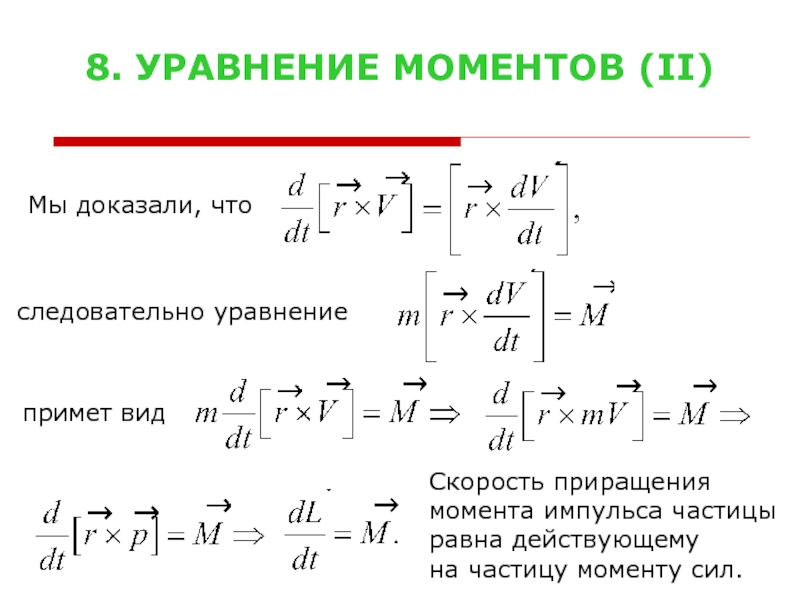
Слайд 118. УРАВНЕНИЕ МОМЕНТОВ (II)
Мы доказали, что
следовательно уравнение
примет
Скорость приращения
момента импульса частицы
равна действующему
на частицу моменту сил.
Слайд 1310. ЗАКОН СОХРАНЕНИЯ
МОМЕНТА ИМПУЛЬСА
Момент импульса замкнутой
(изолированной) системы есть
величина постоянная.
Слайд 1613. МОМЕНТ ИМПУЛЬСА И
МОМЕНТ ИНЕРЦИИ
В общем случае и
совпадают по направлению.
Для однородного тела,
симметричного относительно
оси вращения