динамики вращательного движения.
Момент импульса. Закон сохранения импульса.
Сравнение характеристик и законов поступательного и вращательного движений.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика вращательного движения презентация
Содержание
- 1. Динамика вращательного движения
- 2. Момент силы. Чтобы привести тело во вращение,
- 3. Момент силы. Произведением силы на плечо называется
- 4. Правило рычага Каким ключом проще открутить болт:
- 5. Правило рычага Какие физические величины уравновешиваются при
- 6. Момент инерции. Масса не может служить мерой
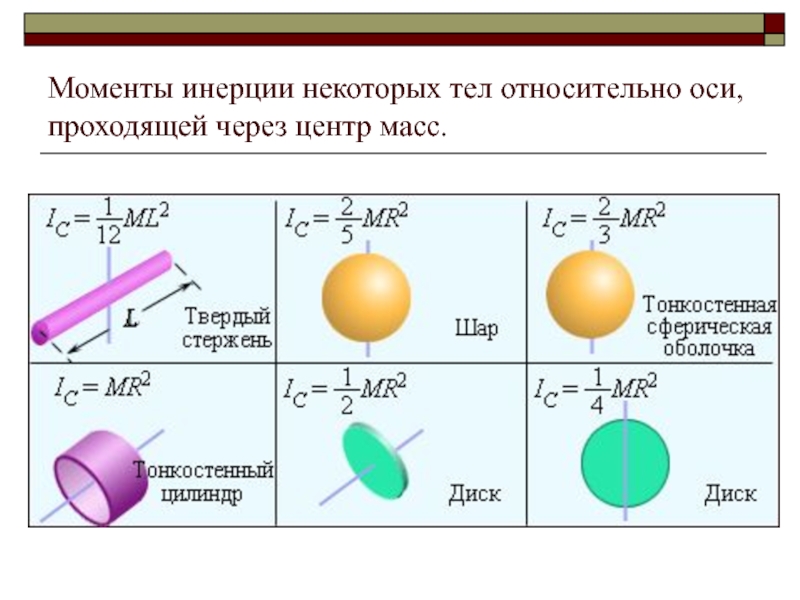
- 7. Моменты инерции некоторых тел относительно оси, проходящей через центр масс.
- 8. Теорема Штейнера. Момент инерции тела относительно произвольной
- 9. Кинетическая энергия вращения. Рассмотрим абсолютно твердое тело,
- 10. Основной закон динамики вращательного движения. Под действием
- 11. Основной закон динамики вращательного движения. Работа идет
- 12. Момент импульса вращающегося тела. Моментом импульса (количества
- 13. Закон сохранения момента импульса. Момент импульса замкнутой
- 14. Сравнение характеристик и законов поступательного и вращательного движений.
Слайд 1Динамика вращательного движения.
Момент силы.
Момент инерции. Теорема Штейнера.
Кинетическая энергия вращающегося тела.
Основной закон
Слайд 2Момент силы.
Чтобы привести тело во вращение, необходимо хотя бы к одной
точке
( А ) приложить внешнюю силу F.
Линия действия силы не должна проходить через ось вращения ( О ).
Радиус-вектор r проводится от оси вращения О до точки приложения силы А.
Угол α между r и F.
Плечом силы называется кратчайшее расстояние от оси до линии действия силы l = r sin α
Линия действия силы не должна проходить через ось вращения ( О ).
Радиус-вектор r проводится от оси вращения О до точки приложения силы А.
Угол α между r и F.
Плечом силы называется кратчайшее расстояние от оси до линии действия силы l = r sin α
Слайд 3Момент силы.
Произведением силы на плечо называется вращающим моментом или моментом силы
относительно оси вращения
М = F l = F r sin α
Направление вектора М определяется по правилу правой руки: четыре согнутых пальца показывают направление движения тела, большой палец показывает направление момента силы.
Вектор М направлен вдоль оси вращения.
М = F l = F r sin α
Направление вектора М определяется по правилу правой руки: четыре согнутых пальца показывают направление движения тела, большой палец показывает направление момента силы.
Вектор М направлен вдоль оси вращения.
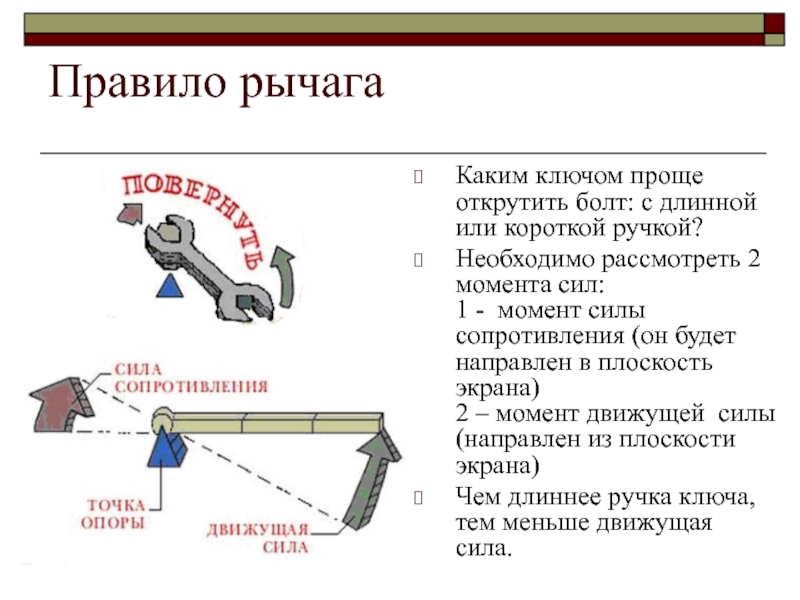
Слайд 4Правило рычага
Каким ключом проще открутить болт: с длинной или короткой ручкой?
Необходимо
рассмотреть 2 момента сил:
1 - момент силы сопротивления (он будет направлен в плоскость экрана)
2 – момент движущей силы (направлен из плоскости экрана)
Чем длиннее ручка ключа, тем меньше движущая сила.
Чем длиннее ручка ключа, тем меньше движущая сила.
Слайд 5Правило рычага
Какие физические величины уравновешиваются при взвешивании на рычажных весах?
Моменты сил.
В
уравновешенном состоянии сила тяжести будет равна приложенной силе только в том случае, если плечи l1 и l2 будут равны.
Слайд 6Момент инерции.
Масса не может служить мерой инертности тела при вращательном движении.
Вводится
понятие момента инерции I.
Моментом инерции материальной точки называется скалярная физическая величина I = m r2
Если вращается твердое тело, состоящее из множества материальных точек, то момент инерции тела находится I = Σ mi ri2.
Момент инерции зависит от массы тела, формы и размеров, ориентации оси вращения.
[ I ] = [ кг·м2 ]
Моментом инерции материальной точки называется скалярная физическая величина I = m r2
Если вращается твердое тело, состоящее из множества материальных точек, то момент инерции тела находится I = Σ mi ri2.
Момент инерции зависит от массы тела, формы и размеров, ориентации оси вращения.
[ I ] = [ кг·м2 ]
Слайд 8Теорема Штейнера.
Момент инерции тела относительно произвольной оси О‘ определяется формулой
I = Io + m d2
где Io – момент инерции тела относительно оси, проходящей через центр масс;
m – масса тела;
d – расстояние между осями.
где Io – момент инерции тела относительно оси, проходящей через центр масс;
m – масса тела;
d – расстояние между осями.
Слайд 9Кинетическая энергия вращения.
Рассмотрим абсолютно твердое тело, вращающееся вокруг оси.
Разобьем его на
маленькие объемы с массами mi , находящихся на расстоянии ri от оси.
Их угловая скорость одинакова w = v1 /r1 = v2 /r2 = …= vi /ri = vn /rn
Кинетическая энергия вращения тела будет равна сумме кинетических энергий объёмов
Их угловая скорость одинакова w = v1 /r1 = v2 /r2 = …= vi /ri = vn /rn
Кинетическая энергия вращения тела будет равна сумме кинетических энергий объёмов
Слайд 10Основной закон динамики вращательного движения.
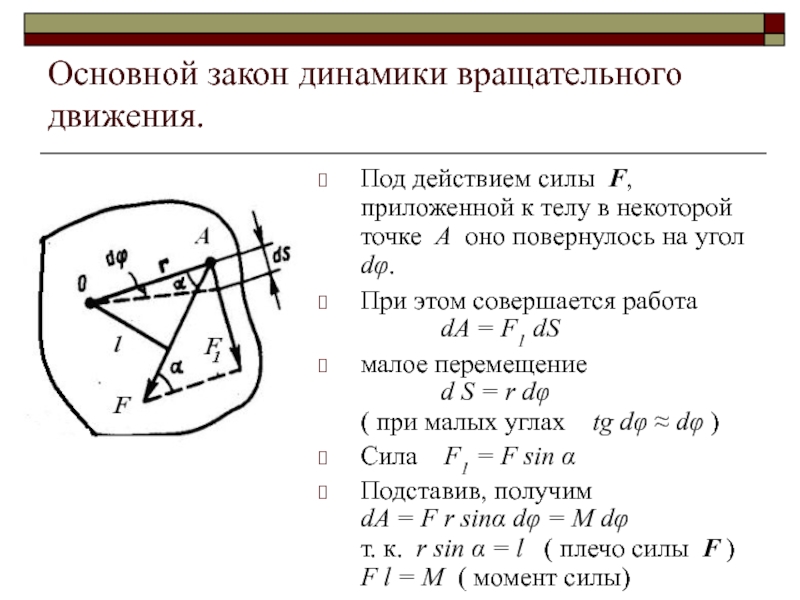
Под действием силы F, приложенной к телу
в некоторой точке А оно повернулось на угол dφ.
При этом совершается работа dA = F1 dS
малое перемещение d S = r dφ ( при малых углах tg dφ ≈ dφ )
Сила F1 = F sin α
Подставив, получим dA = F r sinα dφ = M dφ т. к. r sin α = l ( плечо силы F ) F l = M ( момент силы)
При этом совершается работа dA = F1 dS
малое перемещение d S = r dφ ( при малых углах tg dφ ≈ dφ )
Сила F1 = F sin α
Подставив, получим dA = F r sinα dφ = M dφ т. к. r sin α = l ( плечо силы F ) F l = M ( момент силы)
Слайд 11Основной закон динамики вращательного движения.
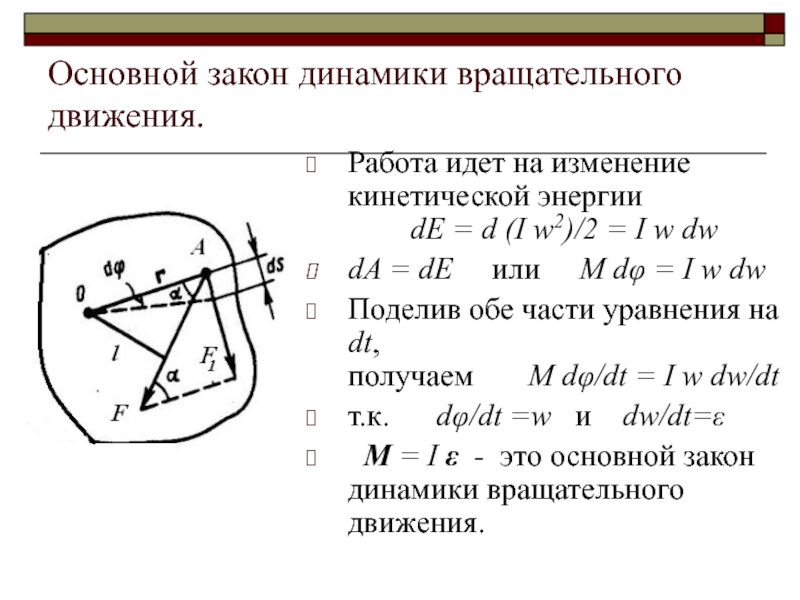
Работа идет на изменение кинетической энергии
dE = d (I w2)/2 = I w dw
dA = dE или M dφ = I w dw
Поделив обе части уравнения на dt, получаем M dφ/dt = I w dw/dt
т.к. dφ/dt =w и dw/dt=ε
M = I ε - это основной закон динамики вращательного движения.
dA = dE или M dφ = I w dw
Поделив обе части уравнения на dt, получаем M dφ/dt = I w dw/dt
т.к. dφ/dt =w и dw/dt=ε
M = I ε - это основной закон динамики вращательного движения.
Слайд 12Момент импульса вращающегося тела.
Моментом импульса (количества движения) материальной точки m
относительно неподвижной точки O называется величина L = [ r mv ] = [ r p ]
Его направление совпадает с направлением правого винта при его вращении от r к p.
Модуль момента импульса L = r p sin α = r mv sin α , где α –угол между векторами r и p.
Момент импульса относительно оси вращения равен L = I w
Его направление совпадает с направлением правого винта при его вращении от r к p.
Модуль момента импульса L = r p sin α = r mv sin α , где α –угол между векторами r и p.
Момент импульса относительно оси вращения равен L = I w
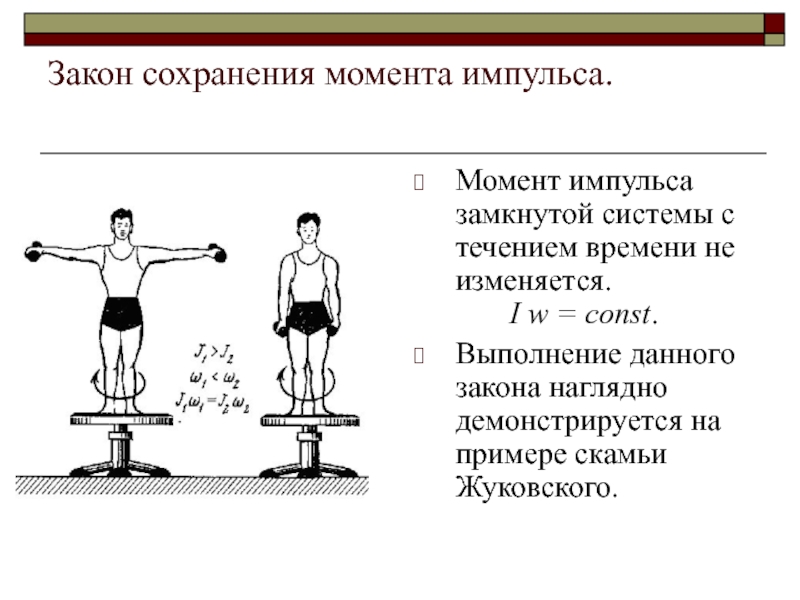
Слайд 13Закон сохранения момента импульса.
Момент импульса замкнутой системы с течением времени не
изменяется.
I w = const.
Выполнение данного закона наглядно демонстрируется на примере скамьи Жуковского.
Выполнение данного закона наглядно демонстрируется на примере скамьи Жуковского.