Министерство по образованию и науки Российской Федерации
ФГАОУ ВПО «Уральский федеральный университет
имени первого Президента России Б.Н.Ельцина»
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика кулисного механизма презентация
Содержание
- 1. Динамика кулисного механизма
- 2. Кулисный механизм
- 3. Задание курсовой работы Кулисный механизм приводится в
- 4. Этап I. Кинематический анализ механизма. Следовательно,
- 5. Этап I. Кинематический анализ механизма. Угловую скорость
- 6. Этап I. Кинематический анализ механизма. Переносное ускорение
- 7. 1.2. Уравнения геометрических связей Как и раньше,
- 8. Этап II. Угловая скорость и угловое ускорение
- 9. Этап II. Угловая скорость и угловое ускорение
- 10. После тождественных преобразований кинетическая энергия системы определяется
- 11. Этап II. Угловая скорость
- 12. Этап III. Реакции связей и уравновешивающая сила.
- 13. Этап III. Реакции связей и уравновешивающая сила.
- 14. Этап IV. Дифференциальное уравнение движения кулисного механизма.
- 15. Этап IV. Дифференциальное уравнение движения кулисного механизма.
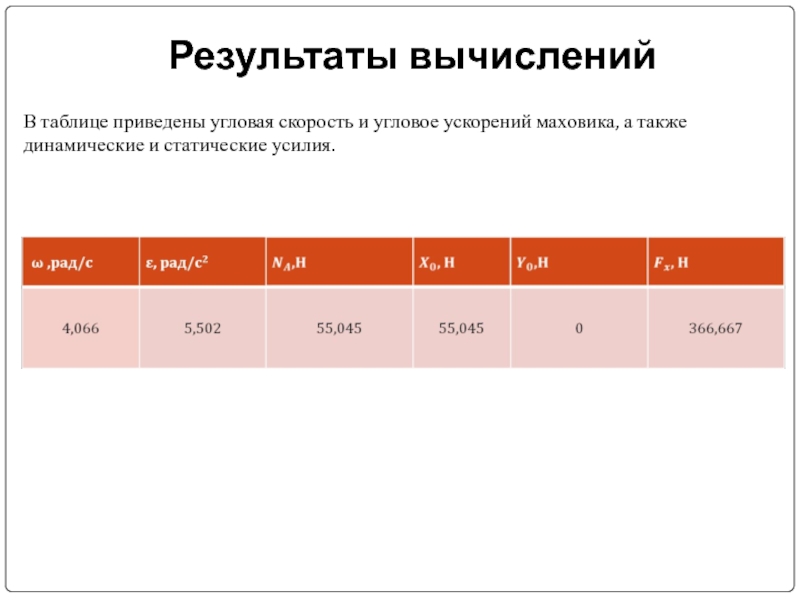
- 16. Результаты вычислений В таблице приведены угловая скорость
Слайд 1Вариант: 2307017
Студент: Крупенин А.Ю.
Группа: М-230701
Преподаватель: Савина Е.А.
КУРСОВАЯ РАБОТА
по теоретической механике
«ДИНАМИКА КУЛИСНОГО
Слайд 3Задание курсовой работы
Кулисный механизм приводится в движение из состояния покоя вращающим
Определить:
Угловую скорость маховика при его повороте на угол .
Угловое ускорение маховика при его повороте на угол .
Силу, приводящую в движение кулису в положении механизма, когда и реакцию подшипника на оси маховика.
Силу, приложенную в центре катка и уравновешивающую механизм в положении, когда .
Слайд 5Этап I. Кинематический анализ механизма.
Угловую скорость катка находим по формуле
Угловое ускорение
Слайд 6Этап I. Кинематический анализ механизма.
Переносное ускорение точки А определяет ускорение кулисы
Ускорение центра катка находим по формуле
Слайд 71.2. Уравнения геометрических связей
Как и раньше, начало координат помещаем в точку
Уравнения связей:
Последние два соотношения получены интегрированием равенств
Слайд 8Этап II. Угловая скорость и угловое ускорение маховика.
2.1 Для определения угловой
Так как по условию задачи механизм приводится в движение из состояния покоя, то
Так как система состоит из абсолютно твердых тел, то работа внутренних сил равна нулю
Слайд 9Этап II. Угловая скорость и угловое ускорение маховика.
Кинетическая энергия вращающегося маховика
Кулиса совершает поступательное движение, следовательно
Кинетическая энергия катка, совершающего плоское движение:
Момент инерции маховика относительно оси вращения определяется формулой
Момент инерции катка вычисляется по формуле
Слайд 10После тождественных преобразований кинетическая энергия системы определяется равенством:
Этап II. Угловая скорость
Элементарная работа определяется равенством:
Работа при повороте маховика на угол φ*
Подставим выражения, полученные для вычисления кинетической энергии и работы внешних сил, в теорему об изменении кинетической энергии
Подставляя числовые значения, получаем
Слайд 11
Этап II. Угловая скорость и угловое ускорение маховика.
2.2 Для определения углового
Вычислим производную от кинетической энергии по времени
Вычислим мощность внешних сил при повороте маховика на угол φ*.
Выразим дифференциальное уравнение движения механизма
Слайд 12Этап III. Реакции связей и уравновешивающая сила.
Маховик совершает вращательное движение.
Система сил
Составим уравнения равновесия.
Сила, приводящая в движение кулису, по третьему закону динамики равна реакции кулисы и направлена в противоположную сторону.
Слайд 13Этап III. Реакции связей и уравновешивающая сила.
Воспользуемся принципом возможных перемещений
Составим уравнение
Используя уравнения связей
находим вариации координат
Подстановка этих соотношений в уравнение принципа виртуальных перемещений дает
Слайд 14Этап IV. Дифференциальное уравнение движения кулисного механизма.
Запишем уравнение Лагранжа второго рода
Обобщенная сила определяется отношением
Тогда
Кинетическая энергия определяется выражением, найденным ранее
Выразим дифференциальное уравнение движения механизма
Слайд 15Этап IV. Дифференциальное уравнение движения кулисного механизма.
Составление уравнения движения машины.
Машиной
Если ведущим звеном является кривошип, то уравнение движения записывается в виде
Приведенный вращающий момент определяется равенством
Для рассматриваемого кулисного механизма
Дифференциальные уравнения движения механизма, полученные с помощью теоремы об изменении кинетической энергии, уравнения Лагранжа и уравнение движения машины совпадают.