А.Е.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика кулисного механизма презентация
Содержание
- 1. Динамика кулисного механизма
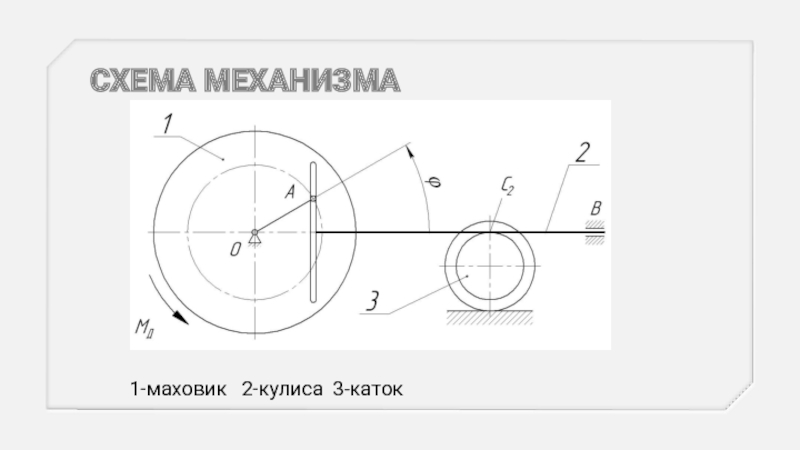
- 2. СХЕМА МЕХАНИЗМА 1-маховик 2-кулиса 3-каток
- 3. УСЛОВИЕ ЗАДАЧИ И ИСХОДНЫЕ ДАННЫЕ Кулисный механизм,
- 4. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА Механизм состоит из
- 5. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ Скорость т.А
- 6. УРАВНЕНИЯ ГЕОМЕТРИЧЕСКИХ СВЯЗЕЙ xA = OA ·
- 7. ОПРЕДЕЛЕНИЕ УГЛОВОЙ СКОРОСТИ МАХОВИКА Для определения
- 8. Кинетическую энергию механизма находим как сумму кинетических
- 9. где I3 = m3 ρ32 – момент
- 10. Определение элементарной работы, мощности внешних сил. Определение
- 11. СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ КУЛИСНОГО МЕХАНИЗМА,ОПРЕДЕЛЕНИЕ УГЛОВОГО
- 12. Воспользуемся теоремой об изменении кинетической энергией в
- 13. Подставляем числовые данные и получаем дифференциальное уравнение
- 14. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ Маховик совершает вращательное движение
- 15. Находим При угле φ* = π/6:
- 16. Действительные направления сил NA и XO соответствуют
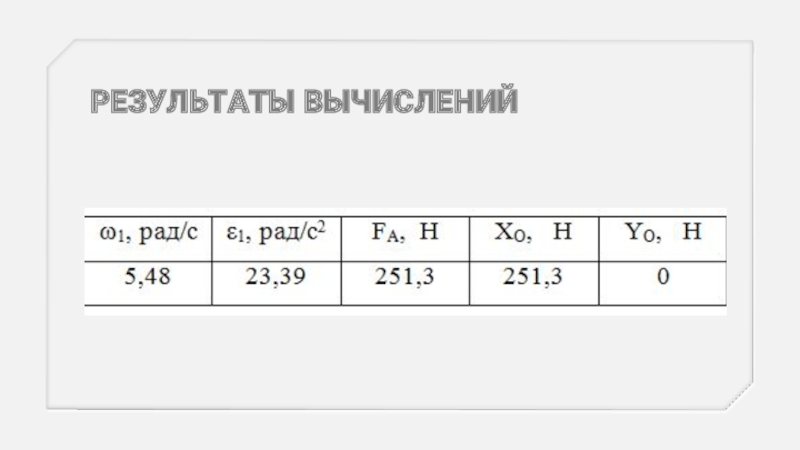
- 17. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
Слайд 1КУРСОВАЯ РАБОТА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Тема: Динамика кулисного механизма.
Выполнила: Орлова П.А.
Группа:ММ-250003
Преподаватель: Ламоткин
Слайд 3УСЛОВИЕ ЗАДАЧИ И ИСХОДНЫЕ ДАННЫЕ
Кулисный механизм, состоящий из маховика 1, кулисы
2 и катка 3, расположен в горизонтальной плоскости и приводится в движение из соcтояния покоя вращающим моментом МД, создаваемым электродвигателем. Заданы массы звеньев механизма; величина вращающего момента; радиус инерции катка и радиусы его ступеней; радиус маховика, представляющего собой сплошной однородный цилиндр, R1 = 0,36 м; OA = 0,24 м.
Слайд 4 КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
Механизм состоит из трех звеньев. Ведущим является
маховик 1, к которому приложен вращающий момент Мд со стороны электродвигателя. От маховика посредством кулисы 2 движение передается ведомому звену 3 – катку.
Маховик совершает вращательное движение, кулиса – поступательное, каток – плоское.
Начало координат помещаем в точку О, ось Ох направляем вправо, ось Оу – вверх
Маховик совершает вращательное движение, кулиса – поступательное, каток – плоское.
Начало координат помещаем в точку О, ось Ох направляем вправо, ось Оу – вверх
Слайд 5КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Скорость т.А
Скорость
кулисы
Ускорение кулисы
Скорость центра катка
Ускорение центра катка
Угловая скорость катка
Угловое ускорение катка
Ускорение кулисы
Скорость центра катка
Ускорение центра катка
Угловая скорость катка
Угловое ускорение катка
Слайд 6УРАВНЕНИЯ ГЕОМЕТРИЧЕСКИХ СВЯЗЕЙ
xA = OA · cos φ;
yA =
OA · sin φ;
xC2 = yC20 + OA · cos φ;
yC2 = 0;
yC3 = r3.
xC2 = yC20 + OA · cos φ;
yC2 = 0;
yC3 = r3.
Слайд 7ОПРЕДЕЛЕНИЕ УГЛОВОЙ СКОРОСТИ МАХОВИКА
Для определения угловой скорости маховика применяем теорему
об изменении кинетической энергии в конечной форме, полагая, что механизм в начальный момент находился в покое.
T – T0 = Ae + Ai где
Т0 = 0 – кинетическая энергия в начальном положении;
Ae = А – работа внешних сил при перемещении механизма из начального положения в конечное;
Ai = 0 – работа внутренних сил при перемещении механизма из начального положения в конечное.
T – T0 = Ae + Ai где
Т0 = 0 – кинетическая энергия в начальном положении;
Ae = А – работа внешних сил при перемещении механизма из начального положения в конечное;
Ai = 0 – работа внутренних сил при перемещении механизма из начального положения в конечное.
Слайд 8Кинетическую энергию механизма находим как сумму кинетических энергий его звеньев
T
= T1 + T2 + T3
Кинетическая энергия вращающегося маховика:
момент инерции маховика (сплошного диска) относительно оси вращения.
Кинетическая энергия поступательно движущейся кулисы:
Кинетическая энергия катка, совершающего плоское движение:
Кинетическая энергия вращающегося маховика:
момент инерции маховика (сплошного диска) относительно оси вращения.
Кинетическая энергия поступательно движущейся кулисы:
Кинетическая энергия катка, совершающего плоское движение:
Слайд 9где I3 = m3 ρ32 – момент инерции катка относительно оси,
проходящей через его центр масс.
Кинетическая энергия системы:
После преобразований: где Iпр(φ) – приведенный к ведущему звену момент инерции механизма, в общем случае зависящий от угла поворота маховика.
Кинетическая энергия системы:
После преобразований: где Iпр(φ) – приведенный к ведущему звену момент инерции механизма, в общем случае зависящий от угла поворота маховика.
Слайд 10Определение элементарной работы, мощности внешних сил. Определение работы внешних сил на
конечном перемещении (механизм в горизонтальной плоскости). В данном механизме нет вертикальных перемещений масс, поэтому работу совершает только вращающий момент МД. Элементарная работа при этом определяется равенством
dAe = МД · dφ
Работа при повороте маховика на угол φ*
ОПРЕДЕЛЕНИЕ УГЛОВОЙ СКОРОСТИ
МАХОВИКА при его повороте на угол
dAe = МД · dφ
Работа при повороте маховика на угол φ*
ОПРЕДЕЛЕНИЕ УГЛОВОЙ СКОРОСТИ
МАХОВИКА при его повороте на угол
Слайд 11СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ КУЛИСНОГО МЕХАНИЗМА,ОПРЕДЕЛЕНИЕ УГЛОВОГО УСКОРЕНИЯ МАХОВИКА
Определение производной кинетической
энергии по времени
Вычисляем для заданных в условии числовых значений:
Мощность
Вычисляем для заданных в условии числовых значений:
Мощность
Слайд 12Воспользуемся теоремой об изменении кинетической энергией в дифференциальной форме
где Ne
– мощность внешних сил; Ni = 0 – мощность внутренних сил.
Подставляя в это уравнение найденные выше значения находим
Подставляя в это уравнение найденные выше значения находим
Слайд 13Подставляем числовые данные и получаем дифференциальное уравнение второго порядка
Это уравнение
описывает движение кулисного механизма. Оно может быть проинтегрировано только численно, а также использовано для нахождения углового ускорения маховика в произвольном его положении
Определим угловое ускорение маховика при угле его поворота φ* = π/6..
Определим угловое ускорение маховика при угле его поворота φ* = π/6..
Слайд 14ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ
Маховик совершает вращательное движение
Система сил инерции приводится к паре
с моментом , направленным против вращения, т.к. оно ускоренное
Условие уравновешенности плоской системы внешних сил
Условие уравновешенности плоской системы внешних сил
Слайд 16Действительные направления сил NA и XO соответствуют показанным на рисунке, т.к.
их величина получилась положительной.
Сила , приводящая в движение кулису, по третьему закону динамики равна реакции кулисы и направлена в противоположную сторону.
Сила , приводящая в движение кулису, по третьему закону динамики равна реакции кулисы и направлена в противоположную сторону.