- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифракция волн презентация
Содержание
- 1. Дифракция волн
- 2. Лекция № 3
- 3. Дифракция – совокупность явлений, обусловленных
- 6. Христиан ГЮЙГЕНС
- 7. Огюст Жан Френель (1788 - 1827)
- 9. Принцип Гюйгенса - Френеля. Построение
- 10. Принцип Гюйгенса - Френеля.
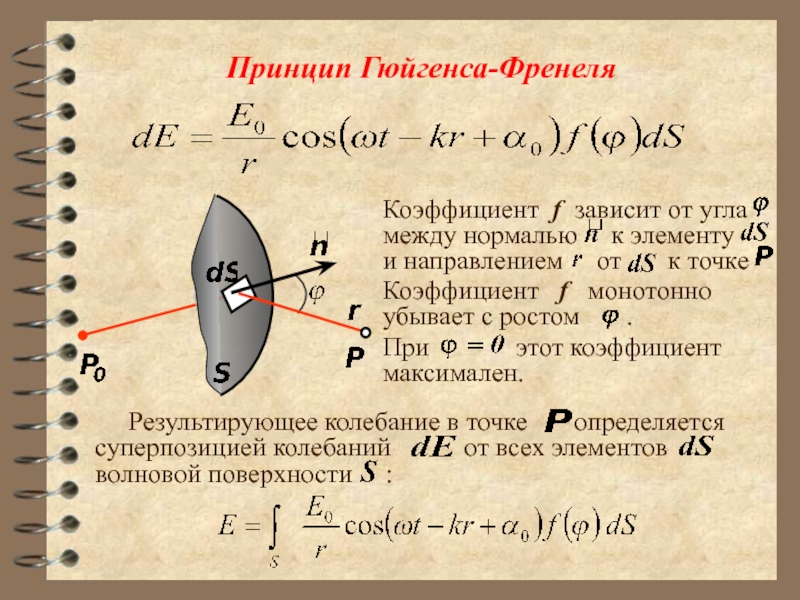
- 12. Принцип Гюйгенса-Френеля
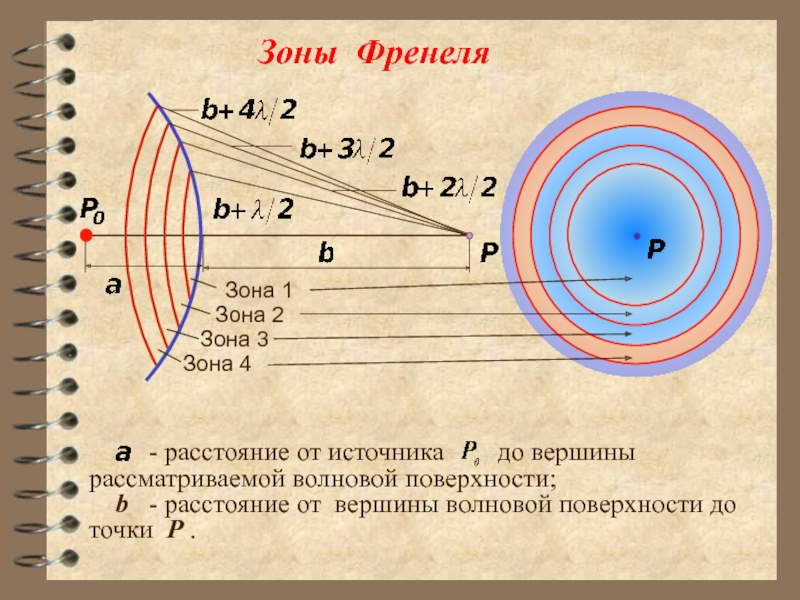
- 20. Зоны Френеля
- 22. Метод векторных диаграмм. Если зону Френеля разбить
- 23. Метод векторных диаграмм. В пределе, при стремлении
- 24. Метод векторных диаграмм. Количественные результаты для осесимметричных
- 33. В т. P всегда наблюдается светлое пятно,
- 34. Картина дифракции на
- 36. Волны, приходящие от зон только с четными
- 37. Зонные пластинки Френеля. Слева - открыты нечетные
- 38. Зонная пластинка Френеля–Соре с успехом применяется в
- 39. Орбитальный телескоп на основе 30-метровой зонной пластинки
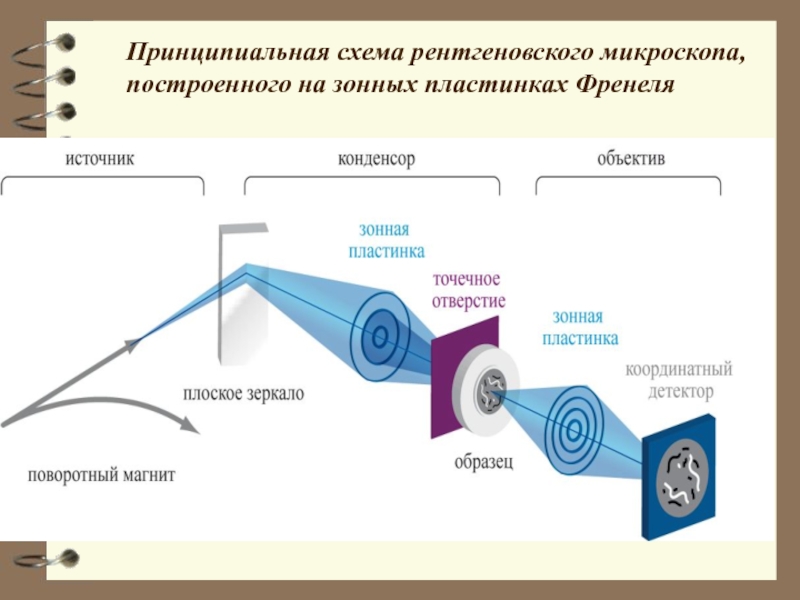
- 40. Принципиальная схема рентгеновского микроскопа, построенного на зонных пластинках Френеля
- 41. ЛЕКЦИЯ ЗАКОНЧЕНА!
- 43. http://www.youtube.com/watch?feature=player_embedded&v=Te8uTReQa9U http://www.youtube.com/watch?feature=player_embedded&v=HtVdgY3GZak#t=64s http://rutube.ru/tracks/3223274.html
- 44. http://rutube.ru/tracks/3223274.html?v=d2e9b72ff871d89795bb7d918e50b9b4&&bmstart=980323
Слайд 2 Лекция № 3
Дифракция
1. Принцип Гюйгенса-Френеля.
2. Зоны Френеля .
3. Метод векторных диаграмм.
4. Осесимметричные задачи
дифракции.
5. Зонная пластинка
Слайд 3 Дифракция – совокупность явлений, обусловленных волновой природой света и
Дифракция приводит к огибанию свето-выми волнами препятствий и проникно-вению света в область геометрич. тени.
Слайд 6 Христиан ГЮЙГЕНС
Christiaan Huygens, 1629–1695
Родился в Гааге в семье дипломата.
Получил хорошее домашнее образо-
вание, затем окончил Лейденский
университет. В 1666 году переехал в
Париж, где принимал участие в организации Академии наук Франции. Самую большую известность Гюйгенсу принесли работы по оптике и астрономии. Он значительно усовершенствовал конструкцию телескопов и открыл кольца Сатурна. Кроме того, Гюйгенс является изобретателем маятниковых часов.
Слайд 7Огюст Жан Френель
(1788 - 1827)
1. Заложил основы теории дифракции света.
2.
3. Заложил основы кристаллооптики.
4. Изучил рефракцию света атмосферой.
5. Разработал систему освещения маяков, в которой важнейшей частью была сконструированная Френелем ступенчатая линза.
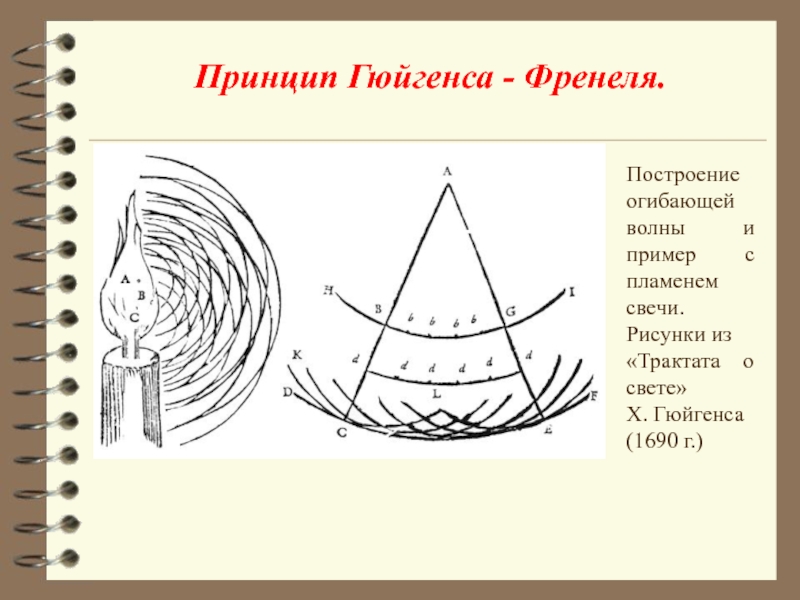
Слайд 9 Принцип Гюйгенса - Френеля.
Построение огибающей волны и пример с
Рисунки из
«Трактата о свете»
Х. Гюйгенса
(1690 г.)
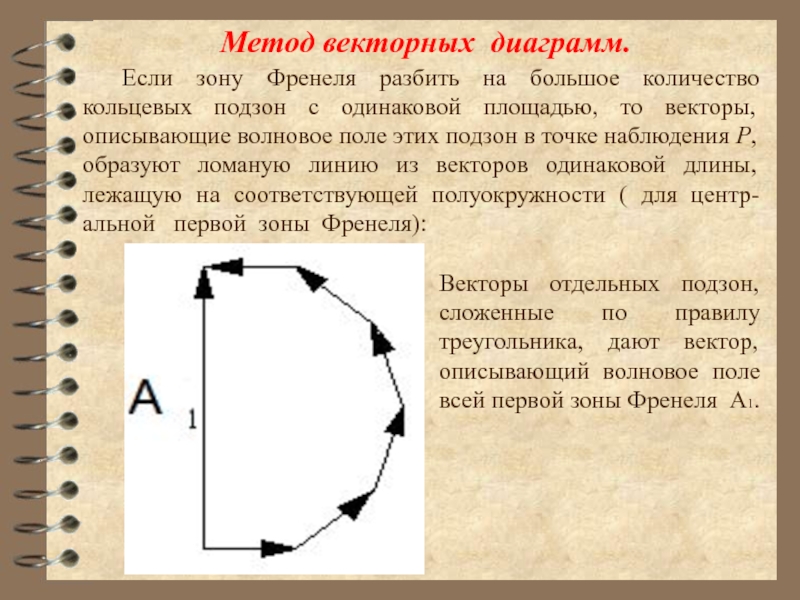
Слайд 22Метод векторных диаграмм.
Если зону Френеля разбить на большое количество кольцевых подзон
Векторы отдельных подзон, сложенные по правилу треугольника, дают вектор, описывающий волновое поле всей первой зоны Френеля А1.
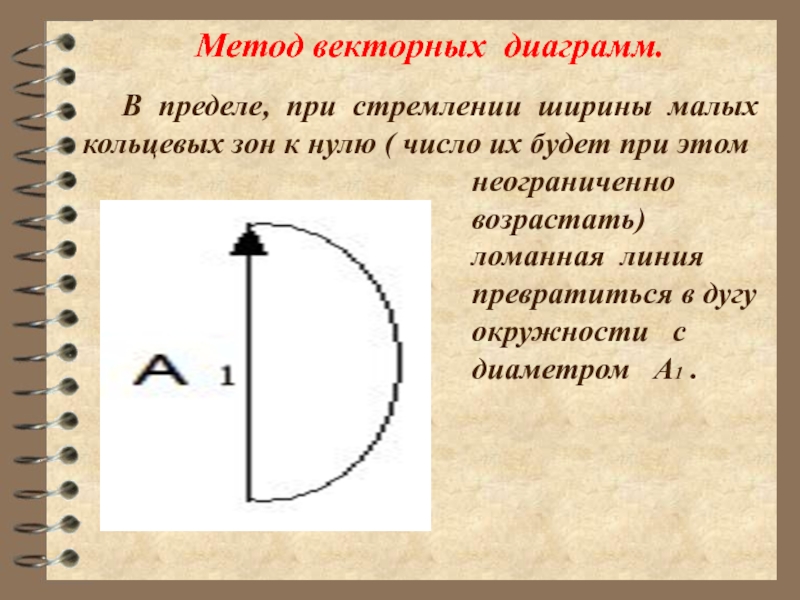
Слайд 23Метод векторных диаграмм.
В пределе, при стремлении ширины малых кольцевых зон к
неограниченно
возрастать)
ломанная линия
превратиться в дугу
окружности с
диаметром А1 .
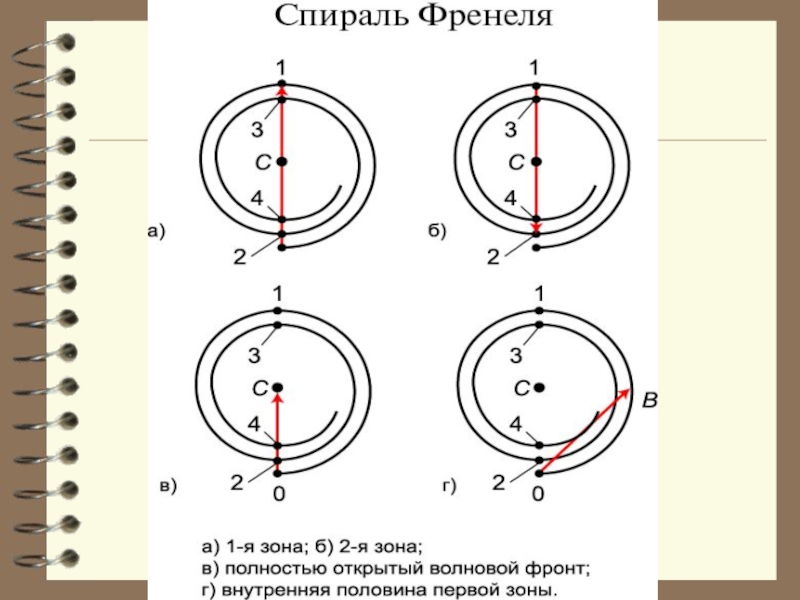
Слайд 24Метод векторных диаграмм.
Количественные результаты для осесимметричных задач дифракции получаются с помощью
Образуется непрерывная спираль (спираль Френеля), которая накручивается на конец результирующего вектора Ар, описывающего суммарное волновое поле в точке наблюдения P. Напомним, что длина вектора Ар в два раза меньше длины вектора А1 .
.
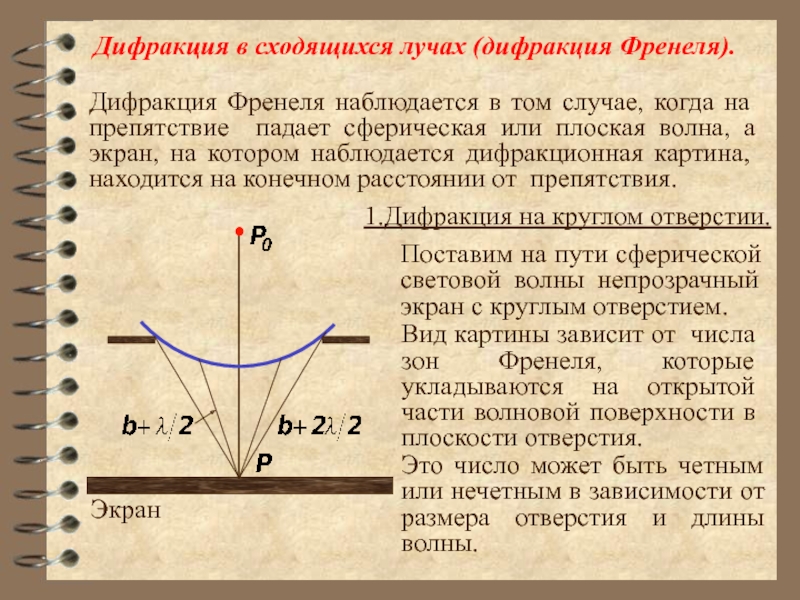
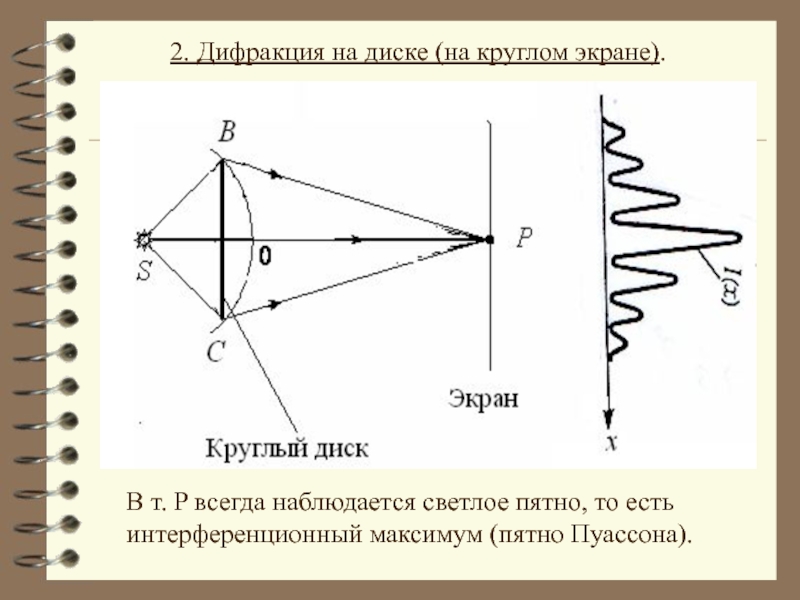
Слайд 33В т. P всегда наблюдается светлое пятно, то есть интерференционный максимум
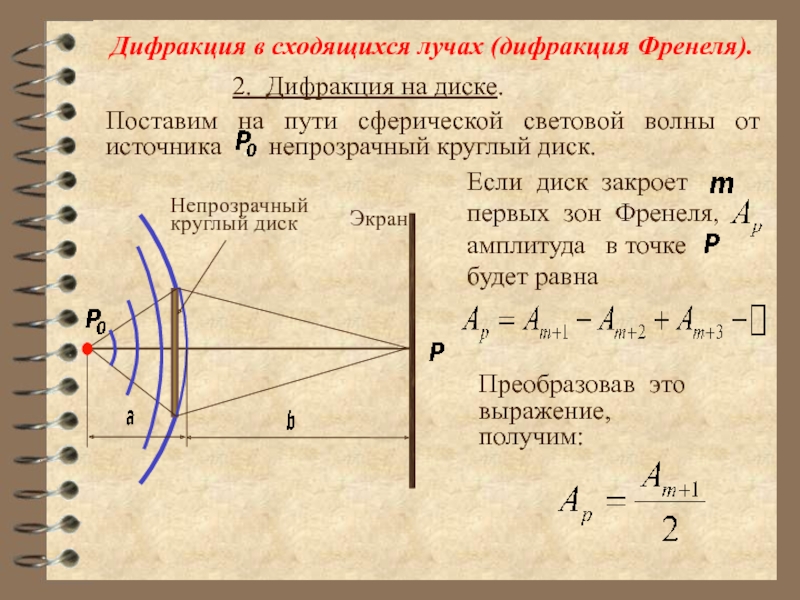
2. Дифракция на диске (на круглом экране).
Слайд 34 Картина дифракции на круглом экране.
Светлое пятно
картины - пятно Пуассона
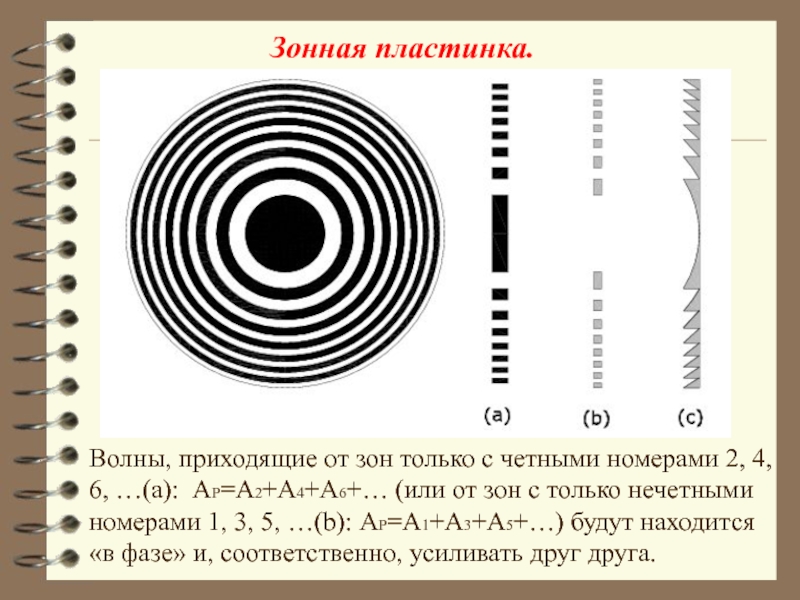
Слайд 36Волны, приходящие от зон только с четными номерами 2, 4, 6,
Зонная пластинка.
Слайд 37Зонные пластинки Френеля. Слева - открыты нечетные зоны, справа – чётные.
Хорошим
Зонная пластинка.
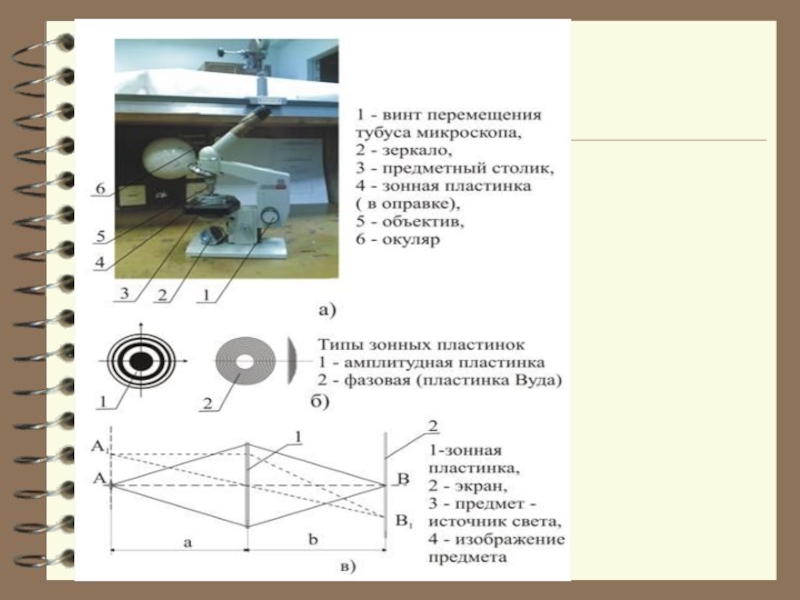
Слайд 38Зонная пластинка Френеля–Соре с успехом применяется в оптике с конца XIX,
Слайд 39Орбитальный телескоп на основе 30-метровой зонной пластинки обладал бы достаточными возможностями
Главная сложность на пути создания орбитального телескопа-дифрактора носит сугубо технический характер. Зонная пластина должна располагаться на одном спутнике, а изображение будет формироваться на другом — в нескольких километрах от первого.