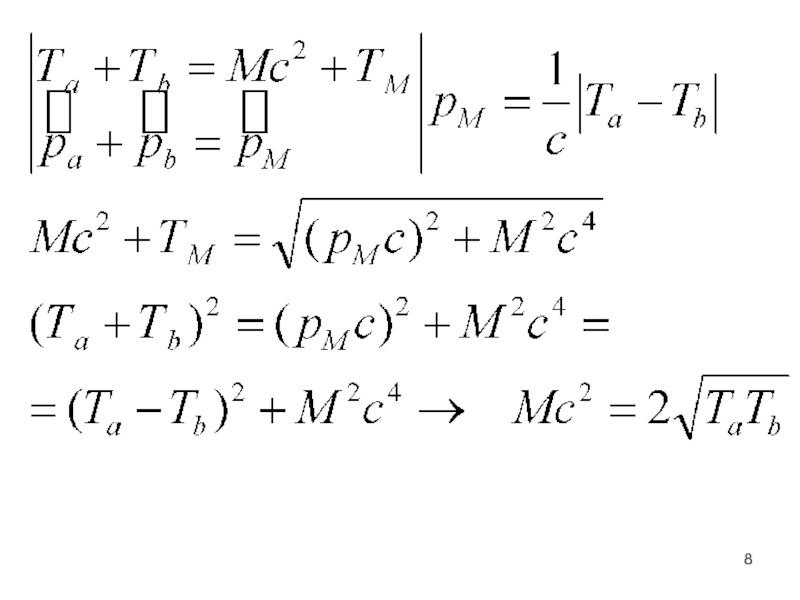- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Частицы и взаимодействия. Ускорители частиц. Элементарные частицы. Экспериментальное исследование структуры частиц. (Лекция 9) презентация
Содержание
- 2. Лекция 9 Частицы и взаимодействия.
- 3. Введение Элементарные частицы – это мир объектов
- 4. 2. Ускорители. Изменение энергии частиц осуществляется
- 6. Заадача 1. Получим формулу , связывающую Та
- 7. Задача 2. Далее, найдем максимальную массу
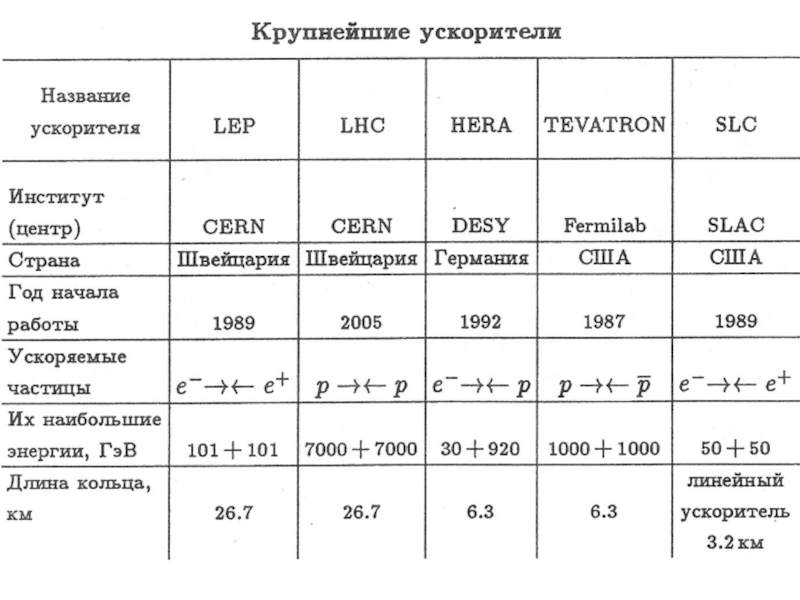
- 9. В ускорителях, заряженные частицы движутся по кольцу,
- 10. 3. Элементарные частицы.
- 12. Их можно рассматривать как возбужденные состояния
- 13. Квазистабильные частицы распадаются медленно,.Трасп>10 -20c , вследствие
- 15. 4. Экспериментальное исследование структуры частиц. Для изучения
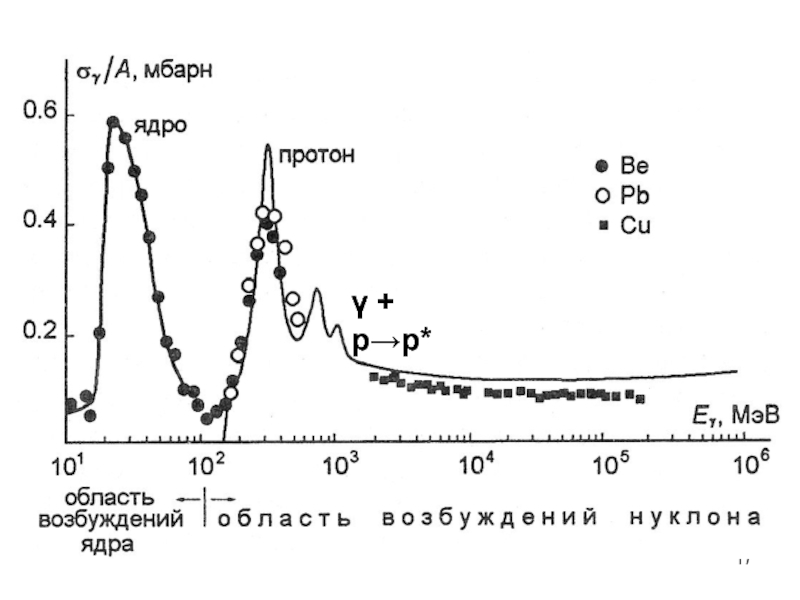
- 16. В 1951г. Ферми обнаружил возбужденное состояние протона в реакции:
- 17. γ + p→p*
- 18. Таким образом, в первом возбужденном состоянии происходит
- 19. 5. Типы, радиусы и константы взаимодействий частиц.
- 20. Нобелевские премии: В 1965 г. Фейман, Швингер,
- 21. 1965 г. – Фейман, Швингер, Томонага –
- 22. ЭСМ и КХД совместно описывают сильное, слабое
- 23. Удобной иллюстрацией процессов в мире частиц являются
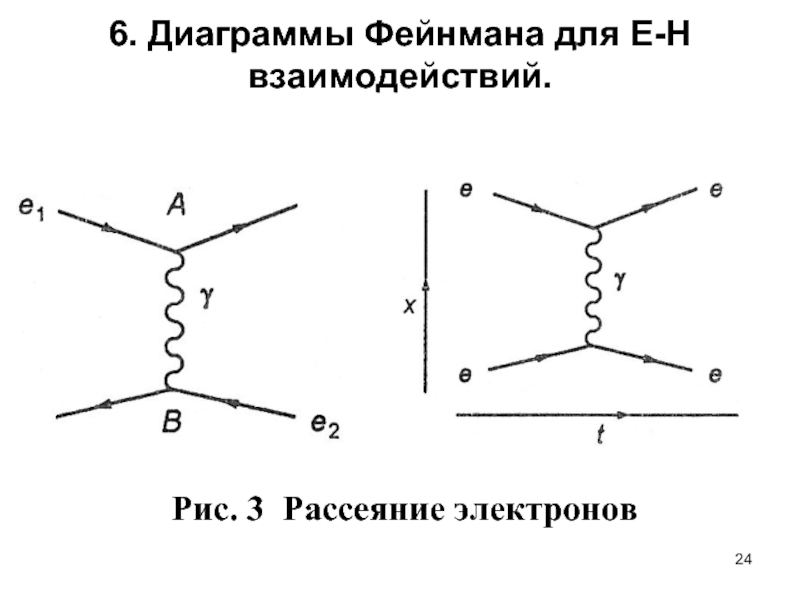
- 24. 6. Диаграммы Фейнмана для Е-H взаимодействий. Рис. 3 Рассеяние электронов
- 25. На рис. 3 представлена типичная диаграмма в
- 26. Согласно квантовой теории поля взаимо-действие между частицами
- 27. В т. B виртуальный γ-квант поглощается и баланс по энергии восстанавливается.
- 28. С помощью таких диаграмм можно рассчи-тать амплитуду
- 29. 2. Степенью нарушения соотношения при рождении виртуальной
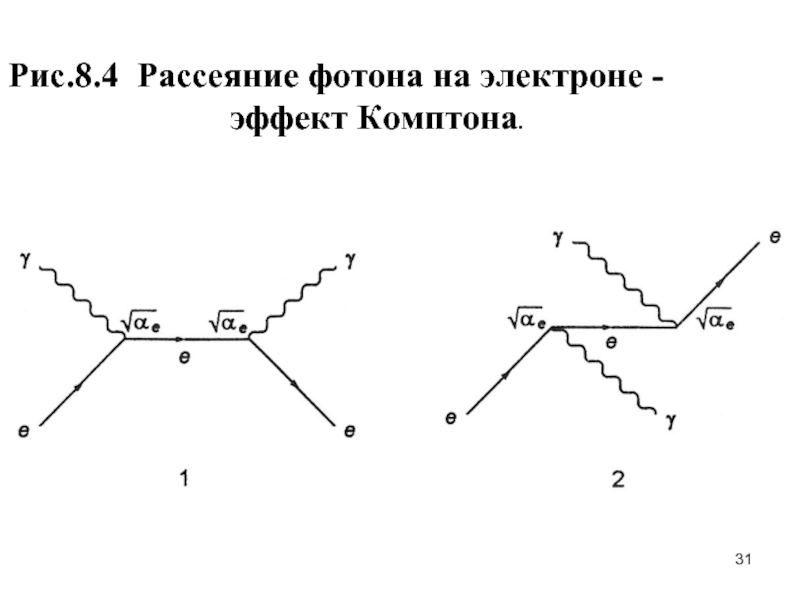
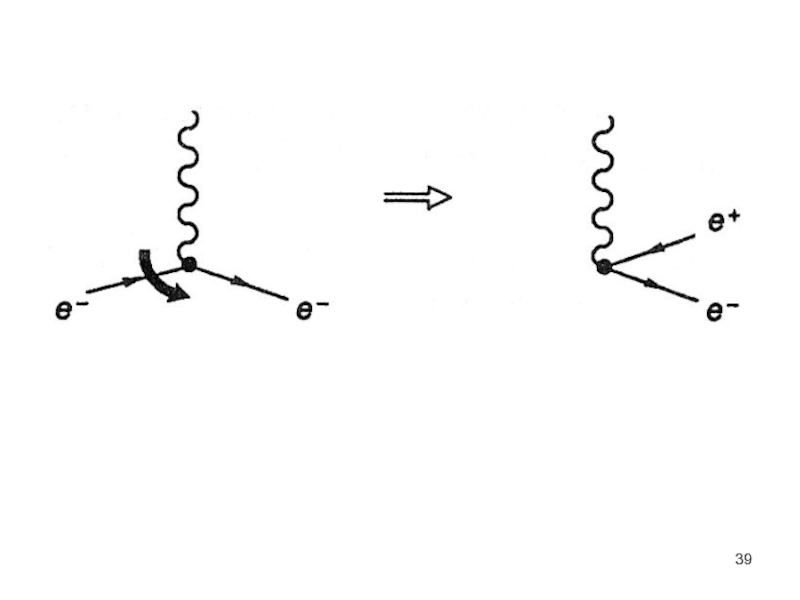
- 30. Пример: Рассеяние фотона на электроне - эффект Комптона.
- 31. Рис.8.4 Рассеяние фотона на электроне -
- 32. Здесь возможны две двухузловые диаграм-мы. В обоих
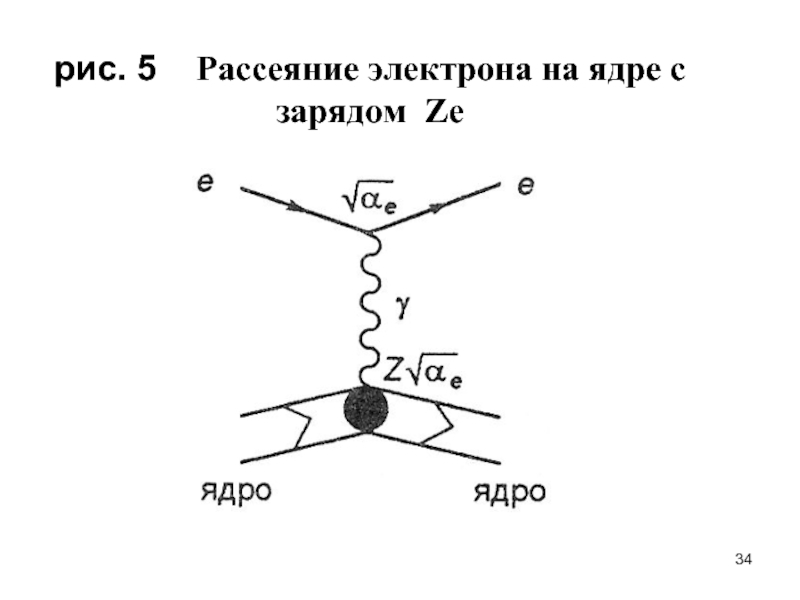
- 34. рис. 5 Рассеяние электрона на ядре с зарядом Ze
- 35. Увеличение числа узлов на диаграмме на два,
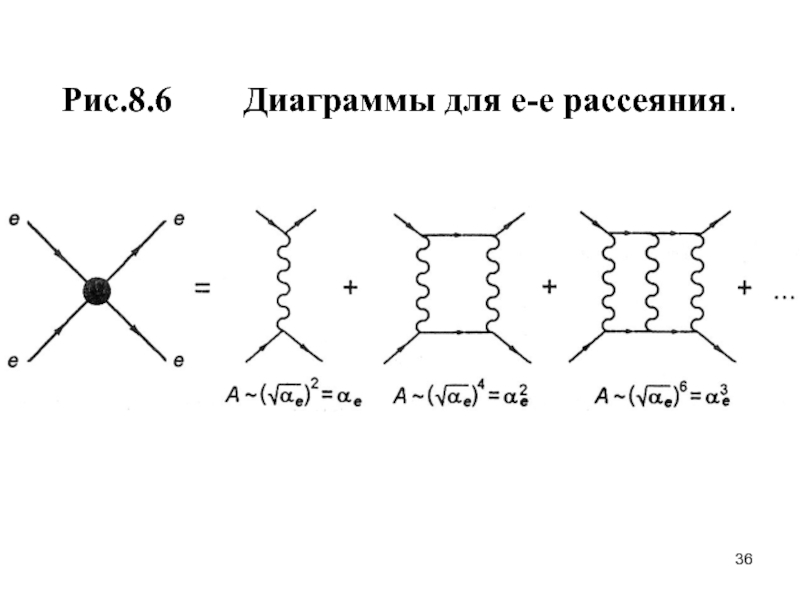
- 36. Рис.8.6 Диаграммы для е-е рассеяния.
- 37. Для слабых взаимодействий подход аналоги-чен. В сильных
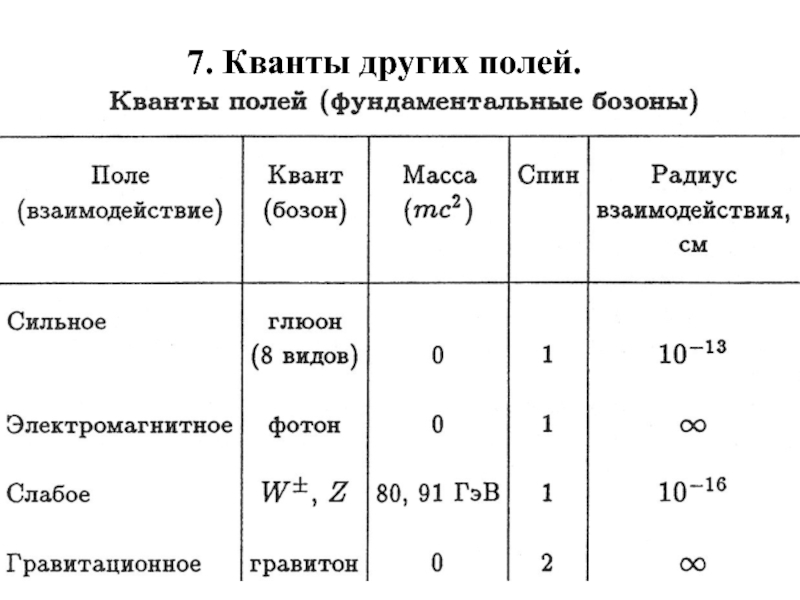
- 38. 7. Кванты других полей.
Лекция 9 Частицы и взаимодействия. Ускорители частиц. Элементарные частицы. 4. Экспериментальное исследование структуры частиц. 5. Типы, радиусы и константы взаимодей-
Слайд 2Лекция 9
Частицы и взаимодействия.
Ускорители частиц.
Элементарные частицы.
4. Экспериментальное
исследование
структуры частиц.
5. Типы, радиусы и константы взаимодей-
ствий частиц.
6. Диаграммы Фейнмана для электромаг-
нитных взаимодействий.
7. Кванты других полей.
структуры частиц.
5. Типы, радиусы и константы взаимодей-
ствий частиц.
6. Диаграммы Фейнмана для электромаг-
нитных взаимодействий.
7. Кванты других полей.
Слайд 3Введение
Элементарные частицы – это мир объектов
~ 1 Фм.
В
настоящее время установлено существование кварков и лептонов, размеры которых ~ 10-3 Фм. и считается, что все сильно взаимодействующие частицы состоят из кварков. Исследование малых областей пространства требует концентрации энергии, поскольку лишь при λ < RЯ возможно проникновение во внутрь ядра:
Слайд 42. Ускорители.
Изменение энергии частиц осуществляется в ускорителях на встречных пучках (коллайде-рах).
Это позволяет исключить потери энергии на движение центра масс, что происходит в линейных ускорителях. Оба типа ускорителей эквивалентны, если mа =mb =m и одинакова энергия, вкладываемая в полезную часть реакции.
Слайд 6Заадача 1. Получим формулу , связывающую Та и Та‘ в эквивалентных
ускорителях, исходя из понятия минимального порога реакции:
Слайд 7
Задача 2. Далее, найдем максимальную массу частицы (М), которую можно получить
на ускорителе на встречных пучках, если:
Та ≠ Тb. Запишем закон сохранения энергии и импульса:
Та ≠ Тb. Запишем закон сохранения энергии и импульса:
Слайд 9В ускорителях, заряженные частицы движутся по кольцу, проходя промежутки с ускоряющим
переменным полем. Частицы увеличивают свою энергию и удерживаются на орбите нарастающим магнитным полем. По достижению Hmax , частицы направляют-ся на неподвижную мишень или во встреч-ный поток частиц.
Слайд 12
Их можно рассматривать как возбужденные состояния стабильных или квазистабильных частиц. Резонансы
распадаются за счет сильных взаимодействий и время
Трасп = 10 -22 -10 -24 с.
Трасп = 10 -22 -10 -24 с.
Слайд 13Квазистабильные частицы распадаются медленно,.Трасп>10 -20c , вследствие элек-тромагнитных или слабых взаимодей-ствий.
Большинство (~450) известных частиц (адроны) состоят из двух кварков (мезоны) или трех кварков (барионы):
адроны↔ мезоны и барионы.
адроны↔ мезоны и барионы.
Слайд 154. Экспериментальное исследование структуры частиц.
Для изучения формы, размеров, распределе-ния электрического заряда
и магнитного момента частиц используют метод упругого рассеяния электронов. Сечение упругого рассеяния электрона на протоне:
Слайд 18Таким образом, в первом возбужденном состоянии происходит переворот спина кварка относительно
исходного состояния. Энергия этого переворота около 300МэВ.
Слайд 195. Типы, радиусы и константы взаимодействий частиц.
В физике фундаментальных взаимодей-ствий наиболее
существенны сильные, электромагнитные и слабые взаимодей-ствия. При экстремально больших массах
(>1019 ГэВ) необходимо учитывать грави-тационные силы. Для описания процессов в мире частиц служит релятивистская кван-товая теория или квантовая теория поля.
(>1019 ГэВ) необходимо учитывать грави-тационные силы. Для описания процессов в мире частиц служит релятивистская кван-товая теория или квантовая теория поля.
Слайд 20Нобелевские премии:
В 1965 г. Фейман, Швингер, Томонага разрабо-тали вариант этой теории
для описания элек-тромагнитных взаимодействий – квантовую электродинамику (КЭД). В 1979 г. Глэшоу, Салам, Вайнберг создали теорию взаимодей-ствия кварков и лептонов, объединяющую электромагнитное и слабое взаимодействие – электрослабая модель (ЭСМ), которая включа-ет КЭД. Для описания сильных взаимодействий разработана квантовая хромодинамика (КХД).
Слайд 211965 г. – Фейман, Швингер, Томонага – КЭД.
1979г. Глэшоу, Салам, Вайнберг
-ЭСМ ( КЭД)
ЭСМ и КХД совместно описывают сильное, слабое и электромагнитное взаимодействие кварков и лептонов и образуют схему, называемую
стандартной моделью.
Слайд 22ЭСМ и КХД совместно описывают сильное, слабое и электромагнитное взаимодействие кварков
и лептонов и образуют схему, назы-ваемую стандартной моделью.
Слайд 23Удобной иллюстрацией процессов в мире частиц являются диаграммы Фейнмана, которые позволяют
оценить вероятности этих процессов взаимодействия. С помощью этих диаграмм можно записать амплитуду вероятности взаимодействия частиц (А) и, просуммировав амплитуды для всех возможных диаграмм процесса, получить эффективное сечение dσ/dΩ.
Слайд 25На рис. 3 представлена типичная диаграмма в осях (x,t). Внешним незамкнутым
линиям отвечают волновые функции реальных частиц до и после взаимодействия.
Внутренним линиям отвечают виртуальные частицы, распространяющиеся от точки испускания до точки поглощения. Функция распространения в этом случае называется пропагатором.
В каждом узле выполняются все законы сохране-ния, присущие данному взаимодействию.
Внутренним линиям отвечают виртуальные частицы, распространяющиеся от точки испускания до точки поглощения. Функция распространения в этом случае называется пропагатором.
В каждом узле выполняются все законы сохране-ния, присущие данному взаимодействию.
Слайд 26Согласно квантовой теории поля взаимо-действие между частицами осуществляется путем обмена некоторой
третьей частицей, которая является квантом поля или пере-носчиком взаимодействия. Например, для электрона взаимодействие осуществляется путем обмена фотоном.
В т.А –узел, вершина диаграммы, испуска-ется γ-квант и электрон испытывает отдачу. При этом нарушается закон сохранения полной энергии, поэтому испускаемый фотон является виртуальным и существует в течение времени
В т.А –узел, вершина диаграммы, испуска-ется γ-квант и электрон испытывает отдачу. При этом нарушается закон сохранения полной энергии, поэтому испускаемый фотон является виртуальным и существует в течение времени
Слайд 28С помощью таких диаграмм можно рассчи-тать амплитуду вероятности, А~α½, выделен-ного процесса
и, просуммировав эти ампли-туды для всех возможных диаграмм, рассчитать эффективное сечение процесса А2. Вероятность процесса взаимодействия зависит от трех факторов:
1. Значения константы α для процесса.
1. Значения константы α для процесса.
Слайд 292. Степенью нарушения соотношения при рождении виртуальной частицы:
3. Полной энергией процесса;
чем выше
энергия, тем выше вероятность.
энергия, тем выше вероятность.
Если узел диаграммы состоит из трех линий, то амплитуда вероятности А процесса:
Слайд 32Здесь возможны две двухузловые диаграм-мы. В обоих случаях виртуальной частицей является
электрон, однако в первом случае происходит поглощение фотона, а во втором –сначала испускание и затем поглощение. Поэтому амплитуда вероятности Комптон-эффекта есть сумма амплитуд соответству-ющих диаграмм:
Слайд 35Увеличение числа узлов на диаграмме на два, уменьшает вероятность процесса в
104 раз. Следовательно, в электромагнитных процессах можно обойтись двухузловыми диаграммами.
Пример: Диаграммы для е-е рассеяния.
Пример: Диаграммы для е-е рассеяния.
Слайд 37Для слабых взаимодействий подход аналоги-чен. В сильных взаимодействиях необходимо учитывать множество
диаграмм, что осложняет расчеты.
В заключение отметим, что каждому взаимо-действию присущ свой заряд: сильный, элек-трический, слабый, гравитационный, соответ-ственно:
В заключение отметим, что каждому взаимо-действию присущ свой заряд: сильный, элек-трический, слабый, гравитационный, соответ-ственно:
