- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Барометрическая формула. Распределение Больцмана презентация
Содержание
- 1. Барометрическая формула. Распределение Больцмана
- 2. 3.4. Барометрическая формула. Распределение Больцмана. Пусть
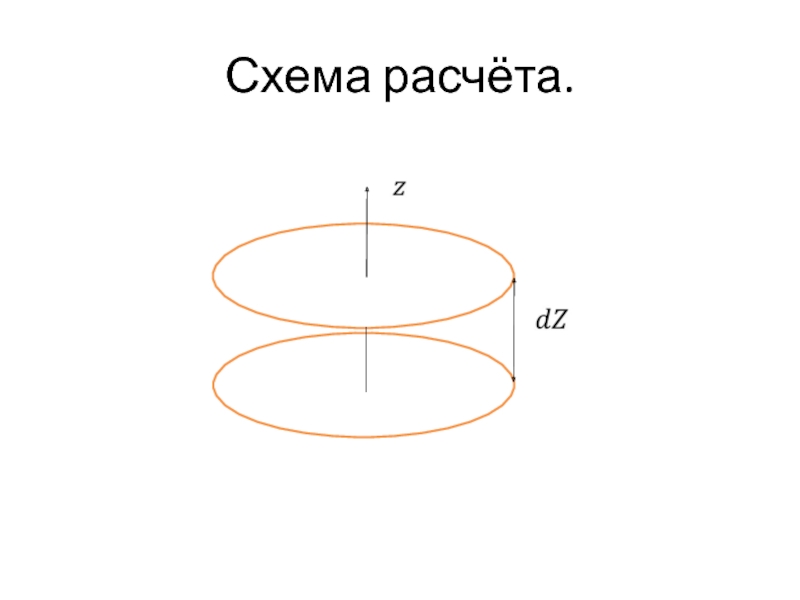
- 3. Схема расчёта.
- 4. Баланс сил.
- 5. Пользуемся уравнением Менделеева-Клапейрона.
- 6. Заменим производную.
- 7. Решение диф. уравнения.
- 8. Отыскание константы.
- 9. Барометрическая формула.
- 10. Формула для концентрации.
- 11. Распределение Больцмана.
- 12. Распределение Больцмана в общем случае.
- 13. С использованием распределения Максвелла.
- 14. Элемент концентрации молекул в потенциальном поле.
- 15. Распределение Максвелла-Больцмана.
- 16. Использование распределения Максвелла-Больцмана.
- 17. Отыскание количества молекул.
- 18. 4. Физическая кинетика. 4.1. Длина свободного пробега
- 19. Кажущееся противоречие. Скорости движения молекул велики. Это
- 20. Объяснение Клаузиуса. Это противоречие впервые объяснил Клаузиус.
- 21. Проверка объяснения Клаузиуса. Progr D: Progr E: Progr F: Progr G: Progr H:
- 22. Трек молекулы.
- 23. Столкновение молекул.
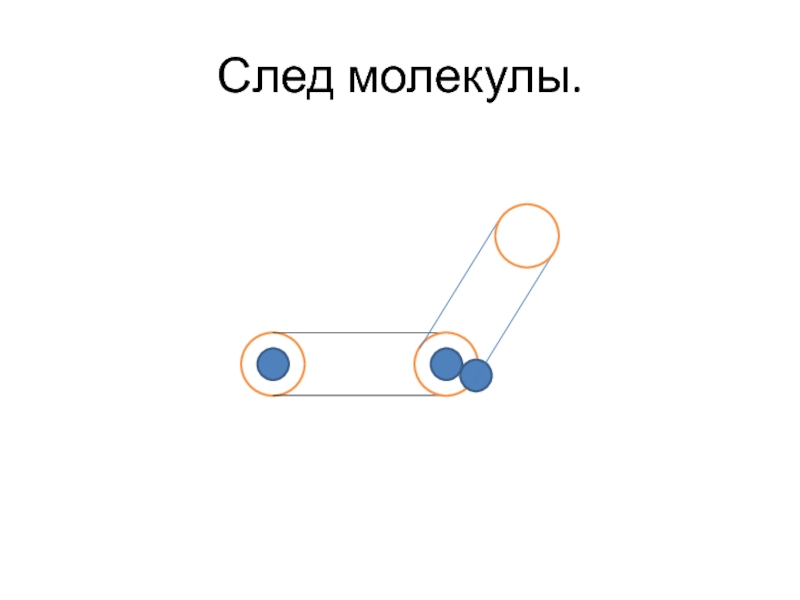
- 24. След молекулы.
- 25. Число молекул, попавших в цилиндр-трек молекулы.
- 26. Усреднённое число столкновений.
- 27. Средняя скорость относительного движения молекул.
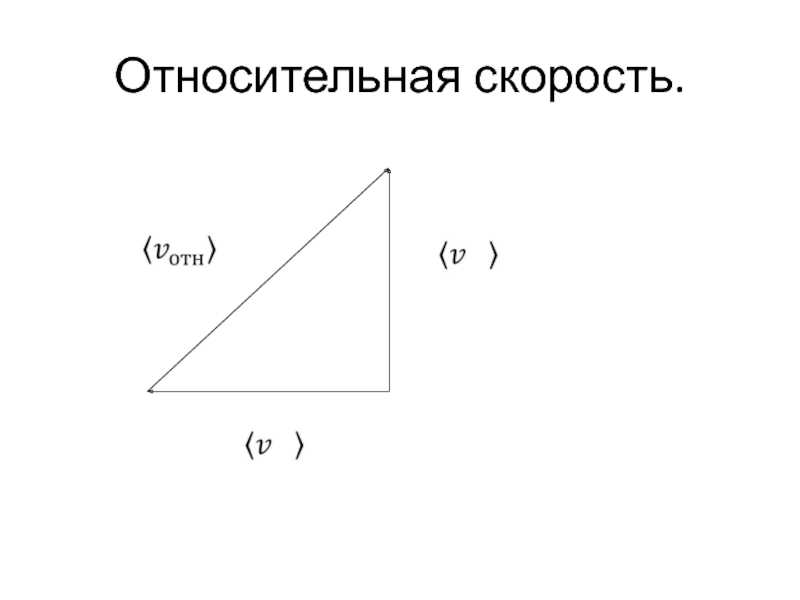
- 28. Относительная скорость.
- 29. Относительная скорость
- 30. Число столкновений молекулы в единицу времени.
- 31. Температурная зависимость числа столкновений.
- 32. Время свободного пробега молекул.
- 33. Длина свободного пробега молекул.
- 34. 4.2. Явление переноса в газах.
- 35. Поток и плотность потока.
- 36. Градиент величины.
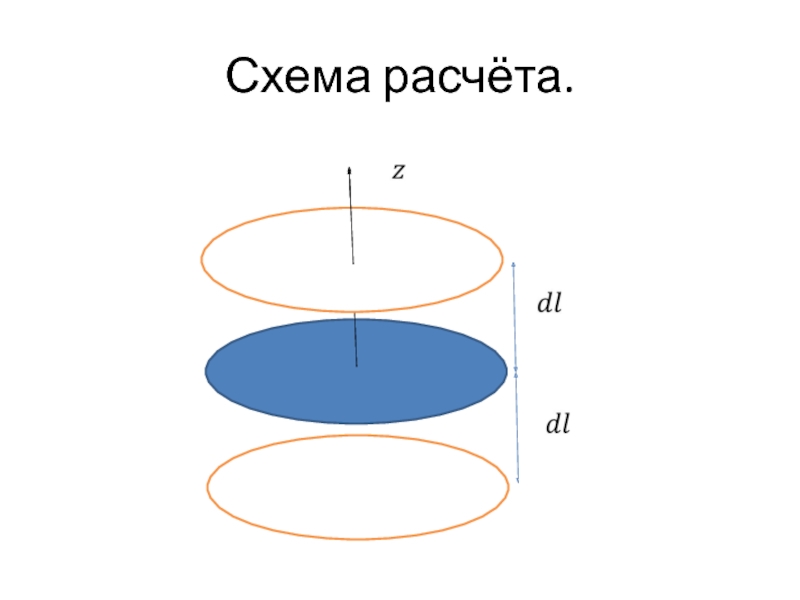
- 37. Схема расчёта.
- 38. Схема расчёта.
- 39.
- 40. Перенос вверх.
- 41. Перенос вниз.
- 42. Общий поток.
- 43. Общий поток с учётом градиента.
- 44.
- 45. Плотность потока в общем случае.
- 46. Формулы явлений переноса.
- 47. Зависимость от концентрации. Однако, это справедливо только
- 48. 4.3. Примеры конкретных явлений переноса.
- 49. Физические причины внутреннего трения При переходе из
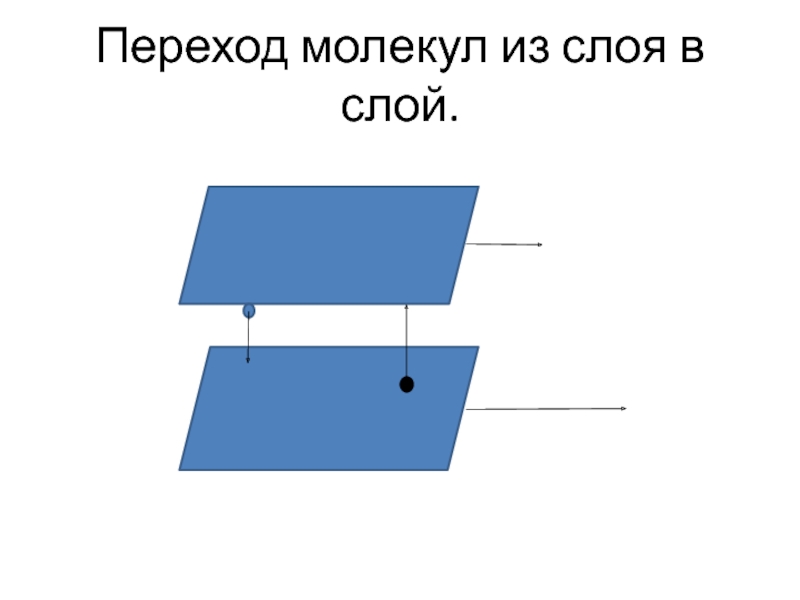
- 50. Переход молекул из слоя в слой.
- 51.
- 52. Сила вязкого трения.
- 53. Коэффициент вязкого трения.
- 54. Зависимость вязкого трения от концентрации. Откуда вновь
- 55. Малая концентрация.
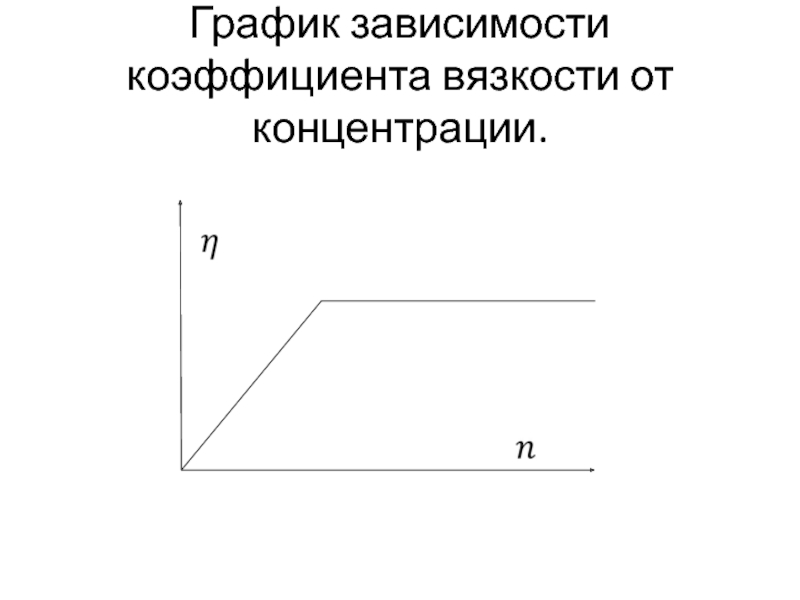
- 56. График зависимости коэффициента вязкости от концентрации.
- 57. Температурная зависимость вязкости
- 58. Согласие с экспериментом. Как видно из этого
3.4. Барометрическая формула. Распределение Больцмана. Пусть в поле силы тяжести находится газ, температура которого во всех точках пространства одинакова. Найдём распределение молекул газа по координатам. Для этого выделим объём в
Слайд 23.4. Барометрическая формула. Распределение Больцмана.
Пусть в поле силы тяжести находится
газ, температура которого во всех точках пространства одинакова. Найдём распределение молекул газа по координатам. Для этого выделим объём в виде цилиндра, образующие которого вертикальны.
Слайд 184. Физическая кинетика.
4.1. Длина свободного пробега молекул, число столкновений молекул в
единицу времени.
Определение. Физической кинетикой называется часть физики, изучающая связь макроскопических термодинамических явлений с микроскопическим движением молекул.
Определение. Физической кинетикой называется часть физики, изучающая связь макроскопических термодинамических явлений с микроскопическим движением молекул.
Слайд 19Кажущееся противоречие.
Скорости движения молекул велики. Это обстоятельство на заре создания молекулярно
кинетической теории было существенным возражением против этой теории. При таких огромных скоростях молекулы должны были бы почти мгновенно долетать от одной стенки сосуда да другой. В то же время запахи распространяются довольно медленно.
Слайд 20Объяснение Клаузиуса.
Это противоречие впервые объяснил Клаузиус. Он предположил, что молекулы не
точечные тела, а имеют конечные размеры. В результате этого от стенки до стенки сосуда они летят не свободно, а сталкиваются с другими молекулами. Это приводит к тому, что траектория движения не прямая, а ломаная линия. И, значит, совершив перемещение от одной стенки сосуда до другой, молекула на самом деле проходит намного больший путь, чем расстояние между стенками.
Слайд 47Зависимость от концентрации.
Однако, это справедливо только до тех пор, пока справедлива
формула длины свободного пробега. При низких давлениях, когда дина свободного пробега молекул становится примерно равной размерам сосуда, она перестаёт зависеть от концентрации молекул. В этом случае для описания явлений переноса нужно пользоваться исходными формулами, в которых длину свободного пробега считать постоянной и равной размерам сосуда. Тогда коэффициенты переноса будут пропорциональны концентрации и с уменьшением концентрации пропорционально будут уменьшаться.
Слайд 49Физические причины внутреннего трения
При переходе из одного слоя газа в другой
молекулы переносят с собой и свой импульс, что приводит к замедлению или к ускорению данного слоя. В результате возникает сила внутреннего трения, стремящаяся замедлить быстрые слои и ускорить медленные.
Слайд 54Зависимость вязкого трения от концентрации.
Откуда вновь следует независимость коэффициента вязкости от
концентрации молекул, пока длина свободного пробега меньше размеров сосуда.
Слайд 58Согласие с экспериментом.
Как видно из этого выражения, коэффициент вязкости прямо пропорционален
корню квадратному из температуры. Эксперимент показывает, что на самом деле рост несколько быстрее. Это, по-видимому, связано с температурной зависимостью длины свободного пробега.
