- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на шесть функций сложного процента. Формулы, калькулятор, Еxсel презентация
Содержание
- 1. Задачи на шесть функций сложного процента. Формулы, калькулятор, Еxсel
- 2. Теория ОСНОВНЫЕ ПОНЯТИЯ PV – текущая
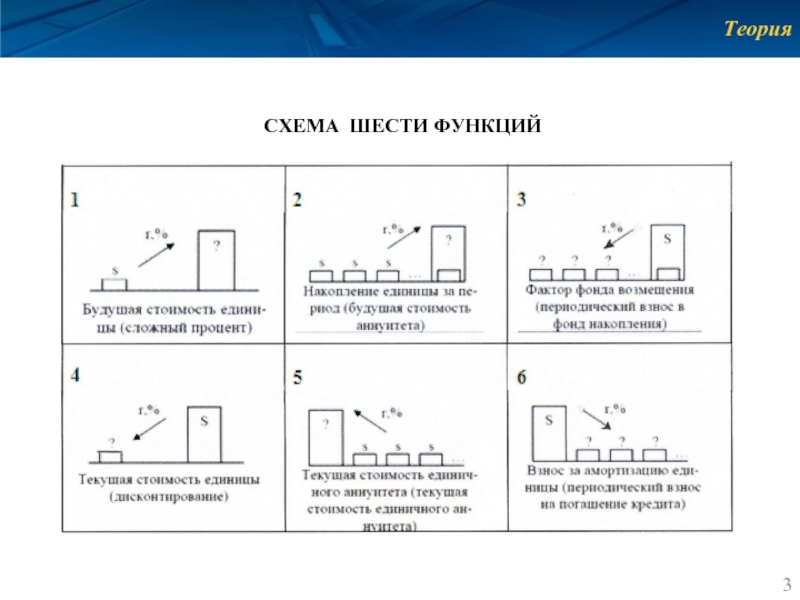
- 3. Теория СХЕМА ШЕСТИ ФУНКЦИЙ
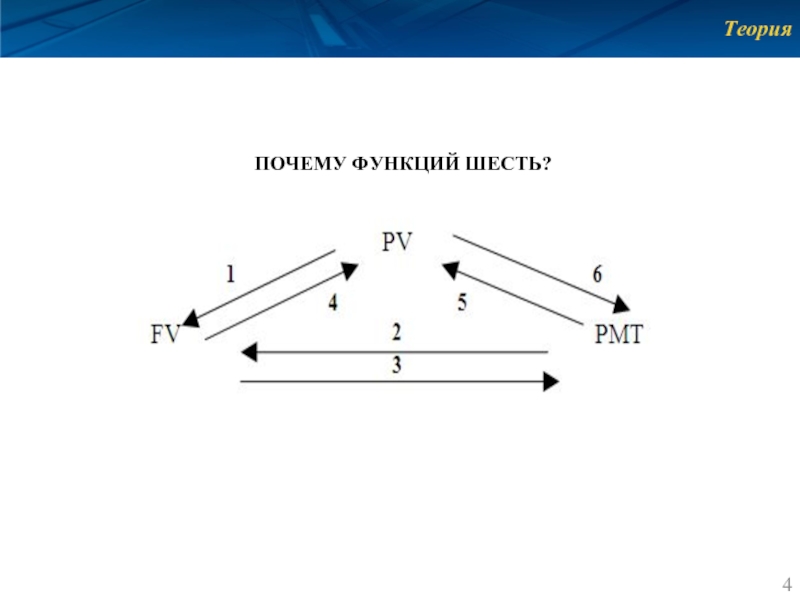
- 4. Теория ПОЧЕМУ ФУНКЦИЙ ШЕСТЬ?
- 5. Теория ОСНОВНЫЕ ФОРМУЛЫ
- 6. Теория ОСНОВНЫЕ ФОРМУЛЫ
- 7. Теория ОСНОВНЫЕ ФОРМУЛЫ 3. Фактор
- 8. Теория ОСНОВНЫЕ ФОРМУЛЫ
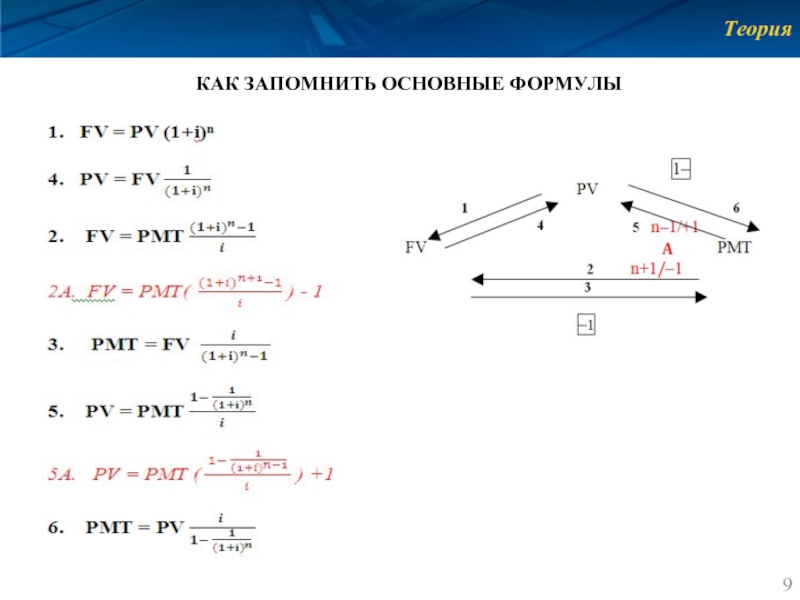
- 9. Теория КАК ЗАПОМНИТЬ ОСНОВНЫЕ ФОРМУЛЫ
- 10. Теория ЗАДАНИЕ Начертите
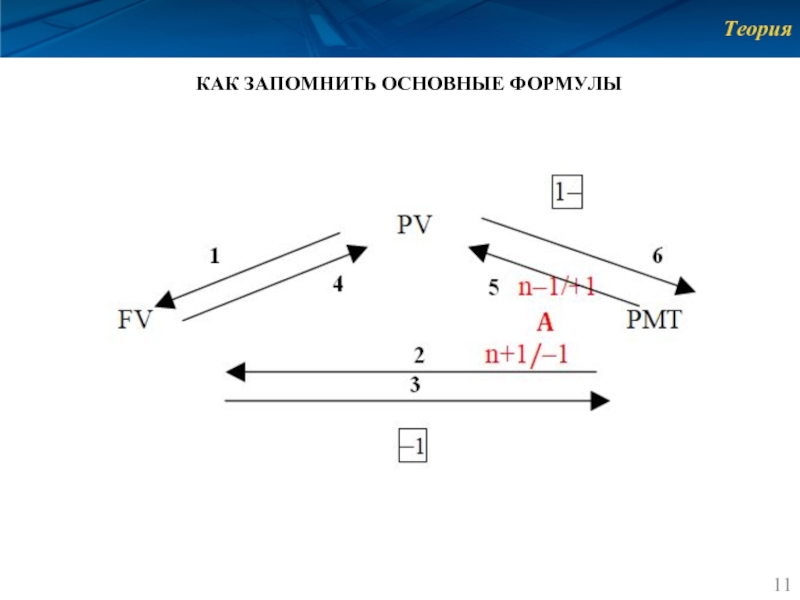
- 11. Теория КАК ЗАПОМНИТЬ ОСНОВНЫЕ ФОРМУЛЫ
- 12. Теория ТЕСТОВЫЕ ВОПРОСЫ Какая функция
- 13. Теория ОТВЕТЫ НА ТЕСТОВЫЕ ВОПРОСЫ
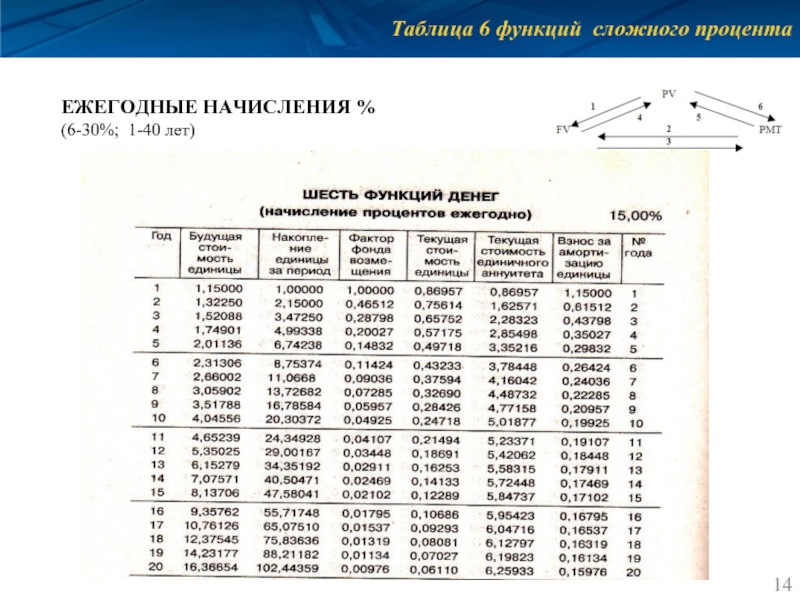
- 14. Таблица 6 функций сложного процента ЕЖЕГОДНЫЕ
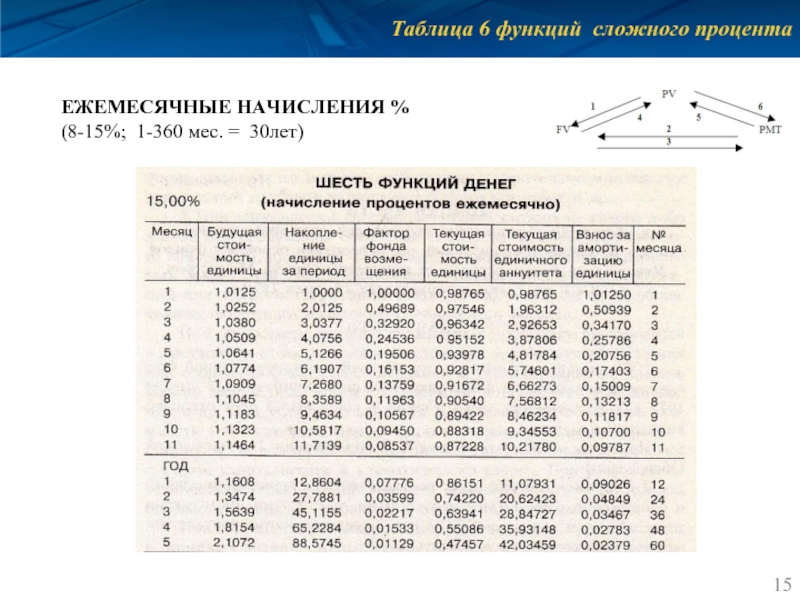
- 15. Таблица 6 функций сложного процента ЕЖЕМЕСЯЧНЫЕ
- 16. Таблица 6 функций сложного процента
- 17. Теория Взаимосвязь формул, калькулятора и Exsel
- 18. Типовые задачи
- 19. Типовые задачи
- 20. Типовые задачи
- 21. Первая функция. Формулы 1.
- 22. Первая функция. Формулы
- 23. Четвертая функция. Формулы
- 24. Четвертая функция. Формулы
- 25. Вторая функция. Формулы 2. Собственник
- 26. Вторая функция. Формулы 2. Собственник
- 27. Третья функция. Формулы 3.
- 28. Третья функция. Формулы 3.
- 29. Третья функция. Формулы 3.1. Вы хотите
- 30. Третья функция. Формулы 3.1. Вы хотите
- 31. Пятая функция. Формулы
- 32. Пятая функция. Формулы 5. Сколько
- 33. Пятая функция. Формулы
- 34. Пятая функция. Формулы 5.1. Определить величину
- 35. Шестая функция. Формулы
- 36. Шестая функция. Формулы 6. Какую
- 37. Шестая функция. Формулы
- 38. Шестая функция. Формулы 6.1. Какими
- 39. Две функции. Формулы Владелец автобуса предполагает
- 40. Две функции. Формулы
- 41. Две функции. Формулы 7. Владелец автостоянки предполагает
- 42. Теория САМЫЕ ГЛАВНЫЕ ФОРМУЛЫ
- 43. Калькулятор Подготовка калькулятора: ON/OFF 2nd – RESET
- 44. Финансовый калькулятор Форматирование [2nd][Format]
- 45. Использование калькулятора ОСНОВНЫЕ ОПЕРАЦИИ Арифметические
- 46. Первая функция. Калькулятор
- 47. Четвертая функция. Калькулятор
- 48. Вторая функция. Калькулятор 2. Собственник
- 49. Третья функция. Калькулятор 3.
- 50. Третья функция. Калькулятор 3.1. Вы хотите
- 51. Пятая функция. Калькулятор 5. Сколько
- 52. Пятая функция. Калькулятор 5.1. Определить величину
- 53. Шестая функция. Калькулятор 6. Какую
- 54. Шестая функция. Калькулятор 6.1. Какими
- 55. Две функции. Калькулятор 7. Владелец автобуса предполагает
- 56. Использования калькулятора Расчет нормы возврата капитала Фактор
- 57. Использования калькулятора Расчет дисконтного множителя Текущая
- 58. ДДП. Калькулятор 8. Годовой арендный платеж
- 59. ДДП. Калькулятор 8. Годовой арендный платеж первые
- 60. ДДП. Калькулятор Порядок расчета:
- 61. ДДП. Калькулятор 9. Сданный в
- 62. ДДП. Калькулятор 9. Сданный в аренду
- 63. ДДП. Калькулятор Порядок расчета:
- 64. EXSEL ОБОЗНАЧЕНИЯ В EXSEL
- 65. EXSEL ПОСЛЕДОВАТЕЛЬНОСТЬ РАБОТЫ В EXSEL
- 66. EXSEL
- 67. EXSEL
- 68. EXSEL
- 69. EXSEL
- 70. EXSEL Решение в Exsel 1.
- 71. EXSEL Решение в Exsel
- 72. EXSEL Решение в Exsel
- 73. EXSEL Решение в Exsel
- 74. EXSEL Решение в Exsel 5.
- 75. EXSEL Решение в Exsel 6.
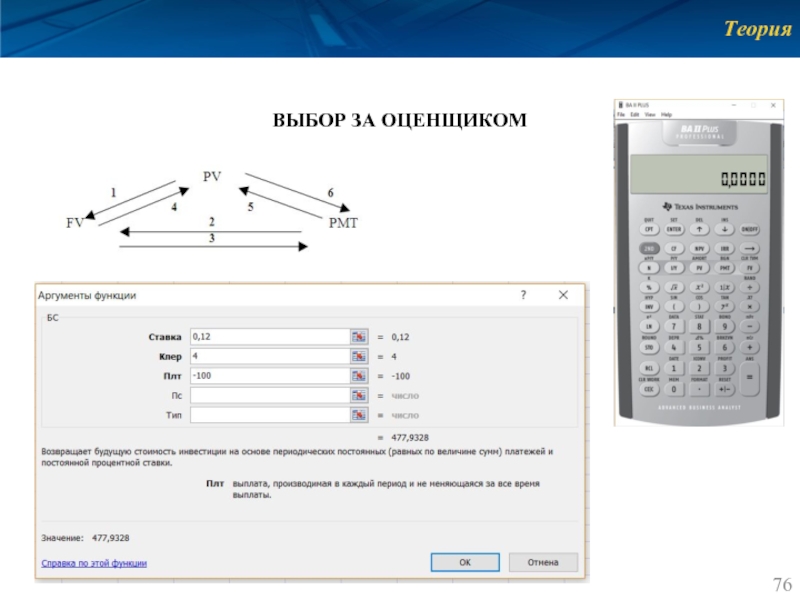
- 76. Теория ВЫБОР ЗА ОЦЕНЩИКОМ
- 77. УСПЕХОВ ПРИ СДАЧЕ КВАЛИФИКАЦИОННОГО ЭКЗАМЕНА !
Слайд 1
Шесть функций сложного процента:
формулы, калькулятор, Еxсel
Вольнова Вера Александровна
сертифицированный РОО оценщик недвижимости
оценщик
Слайд 2Теория
ОСНОВНЫЕ ПОНЯТИЯ
PV – текущая стоимость (present value)
FV - будущая стоимость (future
PMT- платёж, взнос, выплата (payment)
n - число периодов (год)
i - ставка процента за период (годовая)
k – кол. начислений за период (в год)
Аннуитет - серия равномерных равновеликих платежей
Самоамортизирующийся кредит – погашение производится равными по сумме платежами весь срок кредитования и включает часть долга и начисленные проценты
При платежах раз в период и ставке за период (i) (n)
При годовых платежах и годовой ставке (k=1) (i = i) (n = n)
При ежемесячных платежах и годовой ставке (k=12) (i = i/k) (n = nk)
Слайд 5Теория
ОСНОВНЫЕ ФОРМУЛЫ
Будущая стоимость единицы (сложный процент;
сколько будет стоить
FV = PV (1+i)n
Текущая стоимость единицы (дисконтирование;
сколько стоит сегодня то, что получим в будущем)
функция, обратная первой
Годовое или ежемесячное начисление процентов
Слайд 6Теория
ОСНОВНЫЕ ФОРМУЛЫ
2. Будущая стоимость аннуитета
(накопление единицы за период; накопление единицы за
(сколько получим в будущем, если вкладывать по 1 в каждый период)
2.1. (обычного) если платежи в конце каждого года (i = i) (n = n)
2.2. (авансового) если платежи в начале каждого года (i = i) (n = n+1) (-1)
Годовое или ежемесячное начисление процентов
Слайд 7Теория
ОСНОВНЫЕ ФОРМУЛЫ
3. Фактор фонда возмещения (периодический взнос
на накопление фонда; сколько
5. Текущая стоимость аннуитета
(текущая стоимость единичного аннуитета;
сколько сегодня стоит серия будущих выплат в каждый период)
5.1. (обычного) если платежи в конце каждого периода (i = i) (n = n)
5.2. (авансового) если платежи в начале каждого периода (i = i) (n = n-1) (+1)
Годовое или ежемесячное начисление процентов
Фактор фонда возмещения
(сколько платить, чтобы получить 1)
Фактор фонда возмещения
(сколько платить, чтобы получить 1)
Слайд 8Теория
ОСНОВНЫЕ ФОРМУЛЫ
6. Взнос за амортизацию единицы
(периодический взнос
какова величина платежей в каждый период для погашения взятой суммы)
функция, обратная пятой
При годовой ставке и годовых платежах (n = n) (i = i)
При годовой ставке и ежемесячных платежах (n = nk) (i = i/k)
Слайд 10Теория
ЗАДАНИЕ
Начертите схему взаимозависимость шести функций денежной единицы (шести функций
Напишите формулы функций 1 и 4
3. Напишите формулы функций 2 и 3 (двухэтажные)
4. Напишите формулы функций 5 и 6 (трехэтажные)
Слайд 12Теория
ТЕСТОВЫЕ ВОПРОСЫ
Какая функция позволяет определить размер периодического равновеликого взноса для
Если условия накопления заданы годовой процентной ставкой, сроком, выраженным в годах и периодичностью начисления процентов более частой, чем один раз в год, необходимо скорректировать:
А. число периодов накопления.
Б. ставку дохода.
В. оба параметра.
Утверждение о том, что функция «Периодический взнос на накопление фонда» и «Периодический взнос на погашение кредита» находятся в обратной зависимости:
А. верно.
Б. неверно.
Слайд 13Теория
ОТВЕТЫ НА ТЕСТОВЫЕ ВОПРОСЫ
Какая функция позволяет определить размер периодического равновеликого
Если условия накопления заданы годовой процентной ставкой, сроком, выраженным в годах и периодичностью начисления процентов более частой, чем один раз в год, необходимо скорректировать:
А. число периодов накопления.
Б. ставку дохода.
В. оба параметра.
Утверждение о том, что функция «Периодический взнос на накопление фонда» (3 ф) и «Периодический взнос на погашение кредита» (6ф) находятся в обратной зависимости:
А. верно.
Б. неверно.
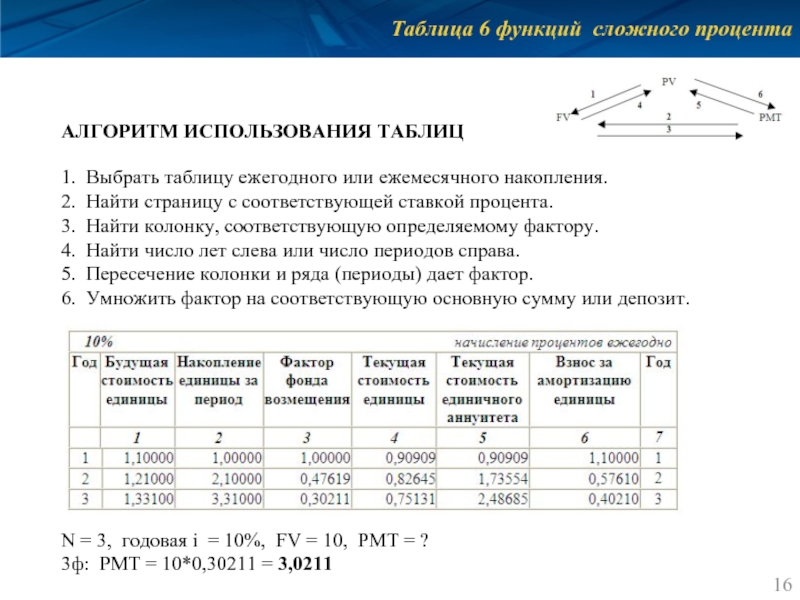
Слайд 16Таблица 6 функций сложного процента
АЛГОРИТМ ИСПОЛЬЗОВАНИЯ ТАБЛИЦ
11
1
1. Выбрать таблицу ежегодного или
2. Найти страницу с соответствующей ставкой процента.
3. Найти колонку, соответствующую определяемому фактору.
4. Найти число лет слева или число периодов справа.
5. Пересечение колонки и ряда (периоды) дает фактор.
6. Умножить фактор на соответствующую основную сумму или депозит.
N = 3, годовая i = 10%, FV = 10, РМТ = ?
3ф: РМТ = 10*0,30211 = 3,0211
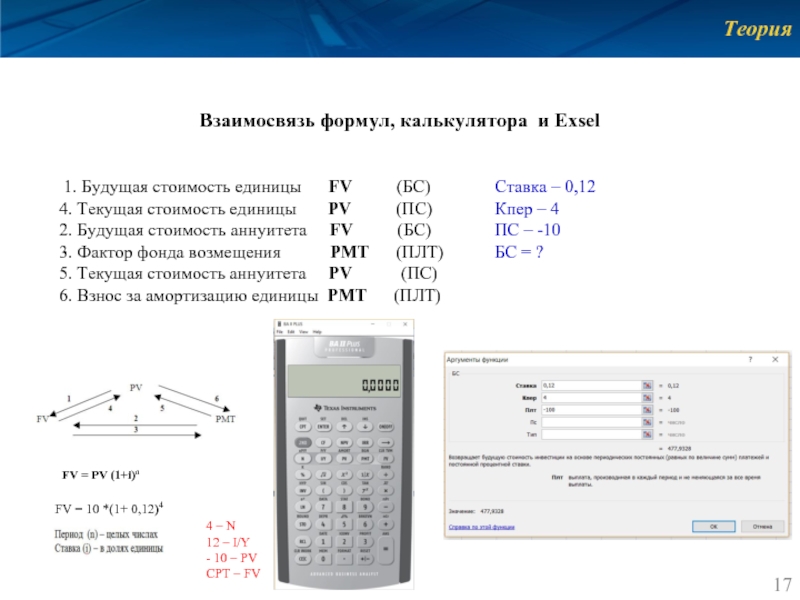
Слайд 17Теория
Взаимосвязь формул, калькулятора и Exsel
1. Будущая стоимость единицы
4. Текущая стоимость единицы PV (ПС) Кпер – 4
2. Будущая стоимость аннуитета FV (БС) ПС – -10
3. Фактор фонда возмещения РМТ (ПЛТ) БС = ?
5. Текущая стоимость аннуитета PV (ПС)
6. Взнос за амортизацию единицы PМТ (ПЛТ)
FV = 10 *(1+ 0,12)4
FV = PV (1+i)n
4 – N
12 – I/Y
- 10 – PV
CPT – FV
Слайд 21Первая функция. Формулы
1. Объект продан за 400 де, деньги приносят 15%
Слайд 22Первая функция. Формулы
1. Объект продан за 400 де, деньги приносят 15%
Формула расчета: FV = PV (1+i)n
FV -?
PV = 400
i = 15%
n = 3
k =1
FV = 400*(1+0,15)3 = 400*1,153 = 608,35 де
Слайд 23Четвертая функция. Формулы
4. Инвестор планирует, что через 3
Слайд 24Четвертая функция. Формулы
4. Инвестор планирует, что через 3
Формула расчета:
PV -?
FV = 2000
i = 11%
n = 3
k = 1
PV = 2 000 * 1/(1+0,11)3 = 2 000* 1/1,113 = 2 000 *0,7312 = 1462,38де
Слайд 25Вторая функция. Формулы
2. Собственник сдает в аренду производственную линию, получая в
Слайд 26Вторая функция. Формулы
2. Собственник сдает в аренду производственную линию, получая в
Формула расчета:
FV -?
РМТ – 1000
i = 12%
n = 4
k = 1
FV = 1000*(1,124 -1)/0,12 = 1000*(1,574-1)/0,12 = 1000*4,78 = 4 780 де.
Слайд 27Третья функция. Формулы
3. Какую одинаковую сумму необходимо ежегодно откладывать собственнику в
Слайд 28Третья функция. Формулы
3. Какую одинаковую сумму необходимо ежегодно откладывать собственнику в
Формула расчета:
РМТ -?
FV = 150
i = 10%
n = 10
k = 1
РМТ = 150 * (0,10/1,110 -1) = 150 *(0,10/1,593) = 150 *0,0627 = 9,412 тыс. руб.
Слайд 29Третья функция. Формулы
3.1. Вы хотите купить автомобиль. Ориентировочная стоимость будущей покупки
Слайд 30Третья функция. Формулы
3.1. Вы хотите купить автомобиль. Ориентировочная стоимость будущей покупки
Формула расчета:
РМТ -?
FV = 70
i = 10%
n = 3
k = 12
i/k = 0,10/12 = 0,0083
n*k =3*12 = 36
РМТ = 70 * 0,0083/(1+0,0083)36 -1 = 70*0,0083/1,008336 -1 =
= 70 * 0,0083/0,347 = 70*0,0239 = 1,675 тыс.де.
Слайд 31Пятая функция. Формулы
5. Сколько стоил объект, купленный в рассрочку на 10
Слайд 32Пятая функция. Формулы
5. Сколько объект, купленный в рассрочку на 10 лет
Формула расчета:
РV -?
РМТ = 1000
i = 13%
n = 10
k = 1
PV = 1000 * (1-1/1,1310 ) / 0,13 = 1000 * (1-0,294)/0,13 = 1000*(0,706/0,13) = 1000*5,43 = 5 430 де.
Слайд 33Пятая функция. Формулы
5.1. Определить величину кредита, если известно что в его
Слайд 34Пятая функция. Формулы
5.1. Определить величину кредита, если известно что в его
Формула расчета:
РV -?
РМТ = 3
i = 10%
n = 4
k = 12
i/k = 0,10/12 = 0,0083
n*k =4*12 = 48
PV = 3 * (1-(1/1,008348 ))/0,0083 = 3*(1-(1/1,487))/0,08 = 3* (1-0,672)/0,0083) = 3* 0,328/0,0083 = 3* 39,458 = 118,3 тыс. де.
Слайд 35Шестая функция. Формулы
6. Какую сумму необходимо ежегодно выплачивать для погашения кредита,
Слайд 36Шестая функция. Формулы
6. Какую сумму необходимо ежегодно выплачивать для погашения кредита,
Формула расчета:
РМТ -?
РV = 30
i = 10%
n = 20
k = 1
РМТ = 30 * 0,10/1- (1/1,120 ) = 30*0,10/(1-0,148) = 30*0,10/0,852 = 30*0,117 = 3,5 тыс. де.
Слайд 37Шестая функция. Формулы
6.1. Какими должны быть ежемесячные выплаты по самоамортизирующемуся кредиту
Слайд 38Шестая функция. Формулы
6.1. Какими должны быть ежемесячные выплаты по самоамортизирующемуся кредиту
Формула расчета:
РМТ -?
РV = 20
i = 10%
n = 5
k = 12
i/k = 0,10/12 = 0,0083
n*k =5*12 = 60
РМТ = 20* 0,0083/ 1-(1/1,008360 )= 20*0,0083/ 1-1/1,642 = 20*0,0083/1-0,609 = 20*0,0083/0,391 = 20* 0,021 = 0,42 тыс. де.
Слайд 39Две функции. Формулы
Владелец автобуса предполагает в течение 6 лет получать ежегодный
Слайд 40Две функции. Формулы
7. Владелец автобуса предполагает в течение 6 лет получать
Алгоритм расчета
Определить текущую стоимость платежей (платеж известен)
Текущая стоимость аннуитета
Определить текущую стоимость продажи (будущая известна)
Текущая стоимость будущей единицы
3. Суммировать текущие стоимости
Слайд 41Две функции. Формулы
7. Владелец автостоянки предполагает в течение 6 лет получать
1 действие
Текущая стоимость аннуитета (5ф)
PV = 60* (1-1/1,156)/0,15 = 60*(1-0,432)/0,15 = 60*0,568/0,1 = 60*3,786 = 227,1 тыс. де.
2 действие
Текущая стоимость будущей единицы (4ф)
PV = 1350*(1/1,126 ) = 1350*1/1,974 = 1350*0,5066 = 683,9 тыс.де.
3 действие
Сумма текущих стоимостей
227,1 + 683,9 = 911,0 тыс.де
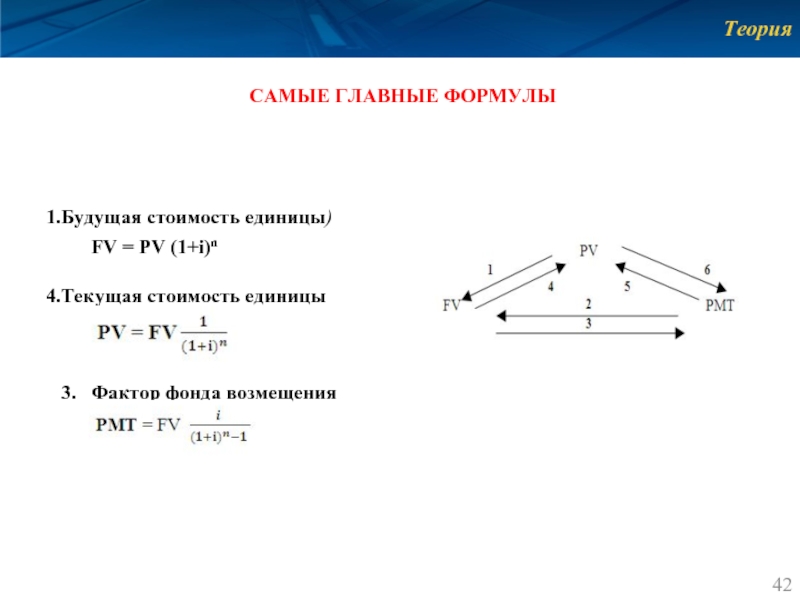
Слайд 42Теория
САМЫЕ ГЛАВНЫЕ ФОРМУЛЫ
Будущая стоимость единицы)
FV = PV (1+i)n
Текущая
3. Фактор фонда возмещения
Слайд 43Калькулятор
Подготовка калькулятора:
ON/OFF
2nd – RESET
ENTER
CE/C
2nd – FORMAT
DEC = 4,000
ENTER [↓]
DEG
ENTER [↓]
US 12-31-1990
2nd – ENTER
EUR 31-12-1990
ENTER [↓]
EUR 1.000,0000
ENTER [↓]
AOS
ENTER
2nd –END
ENTER
CE/C
Период – в целых числах
Ставка – в целых числах (процент)
Слайд 44Финансовый калькулятор
Форматирование
[2nd][Format]
Смена настройки
[2nd][SET]
Выход из режима настройки в режим стандартных вычислений
[2nd][QUIT]
Слайд 45Использование калькулятора
ОСНОВНЫЕ ОПЕРАЦИИ
Арифметические вычисления
Возведение в степень, в квадрат
Извлечение квадратного корня
Вычисление обратной
5. Расчет логарифмов
Работа с памятью
Расчет шести функций сложного процента
Расчет дисконтного множителя (PV от FV=1)
Расчет фактора фонда возмещения (PMT от FV=1)
Расчет текущей стоимости дисконтированного денежного потока
Расчет остатка по кредиту, процентов, выплаченной суммы
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для проведения практических занятий
по курсу «Оценка недвижимости» с применением финансового калькулятора ТI BA II Plus
https://drive.google.com/open?id=0B4EIjNGShp8EYWM4Nm5OaEhFSDQ
Слайд 46Первая функция. Калькулятор
1. Объект продан за 400 де, деньги приносят 15%
FV = 608,35 де
ON/OFF
2nd – CLR TWM
3 – N
15 – I/Y
400 – PV
CPT – FV
608,35 де
Слайд 47Четвертая функция. Калькулятор
4. Инвестор планирует, что через 3
PV = 1462,38 де
ON/OFF
2nd – CLR TWM
3 – N
11 – I/Y
2000 –FV
CPT – PV
1462,38 де
Слайд 48Вторая функция. Калькулятор
2. Собственник сдает в аренду производственную линию, получая в
FV = 4 780 де
ON/OFF
2nd – CLR TWM
4 – N
12 – I/Y
1000 –РМТ
CPT – FV
4 780 де
Слайд 49Третья функция. Калькулятор
3. Какую одинаковую сумму необходимо ежегодно откладывать собственнику в
РМТ = 9,412 тыс. руб.
ON/OFF
2nd – CLR TWM
10 – N
10 – I/Y
150 – FV
CPT – РМТ
9,412 тыс. руб.
Слайд 50Третья функция. Калькулятор
3.1. Вы хотите купить автомобиль. Ориентировочная стоимость будущей покупки
РМТ = 1,675 тыс.де.
N=n*k =3*12 = 36
I/Y:
2nd
Р/Y =12 ENTER [↓]
С/Y =12 ENTER [↓]
CE/C
2nd – CLR TWM
36 – N
10 – I/Y
70 – FV
CPT – РМТ
1,675 тыс.де.
Слайд 51Пятая функция. Калькулятор
5. Сколько стоил объект, купленный в рассрочку на 10
PV = 5 430 де.
2nd – CLR TWM
10 – N
13 – I/Y
1000 – РМТ
CPT – РV
5 430 де.
Слайд 52Пятая функция. Калькулятор
5.1. Определить величину кредита, если известно что в его
PV = 118,3 тыс. де.
N=n*k =4*12 = 48
I/Y:
2nd
Р/Y =12 ENTER [↓]
С/Y =12 ENTER [↓]
CE/C
2nd – CLR TWM
48 – N
10 – I/Y
3 – РМТ
CPT – РV
118,3 тыс. де.
Слайд 53Шестая функция. Калькулятор
6. Какую сумму необходимо ежегодно выплачивать для погашения кредита,
РМТ = 3,5 тыс. де.
2nd – CLR TWM
20 – N
10 – I/Y
30 – РV
CPT – РМТ
3,5 тыс. де.
Слайд 54Шестая функция. Калькулятор
6.1. Какими должны быть ежемесячные выплаты по самоамортизирующемуся кредиту
РМТ = 0,42 тыс. де.
N=n*k =5*12 = 60
I/Y:
2nd
Р/Y =12 ENTER [↓]
С/Y =12 ENTER [↓]
CE/C
2nd – CLR TWM
60 – N
10 – I/Y
20 – РV
CPT – РМТ
0,42 тыс. де.
Слайд 55Две функции. Калькулятор
7. Владелец автобуса предполагает в течение 6 лет получать
Сумма текущих стоимостей
227,1 + 683,9 = 911,0 тыс.де
1. (5 функция РV - ?)
6 – N
15 – I/Y
60 – РМТ
CPT – РV
227,1 тыс. де [STO] 1
(4 функция РV - ?)
6 – N
12 – I/Y
1 350 – FV
CPT – РV
683,9 тыс. де [RCL] 1
сумма:
227,1+683,9 = 911,0 тыс. де
Слайд 56Использования калькулятора
Расчет нормы возврата капитала
Фактор фонда возмещения (3 функция)
Метод Инвуда (СД=12%,
20– N
12 – I/Y
1 – FV
CPT – РМТ = 0,0139 = 1,39%
Метод Хоскальда (БР=8%, ОСЭЖ=30 лет)
15– N
8 – I/Y
1– FV
CPT – РМТ = 0,0368 = 3,68%
3. Метод Ринга (ОСЭЖ=25 лет)
25 [1/x] 0,040 = 0,040 = 4,0%
Слайд 57Использования калькулятора
Расчет дисконтного множителя
Текущая стоимость будущей единицы (четвертая функция)
для 2-го периода:
2
15 – I/Y
1– FV
CPT – РV
Kd = 0,756
для 2-го периода:
не очищая:
3 – N
CPT – РV
Kd = 0,658
ИЛИ:
1,15 Yx 2 = 1/x 0,756
1,15 Yx 3 = 1/x 0,658
Слайд 58ДДП. Калькулятор
8. Годовой арендный платеж первые 2 года составляет 100 тыс.
Какова текущая стоимость потока арендных платежей?
Алгоритм расчета
1. Сформировать потоки дохода по периодам (РМТ)
2. Определить номер периода (n)
3. Определить коэффициент дисконтирования (дисконтный множитель) (Kdn)
4. Рассчитать текущую стоимость дохода каждого периода (PVn)
как произведение: PVn * Kdn
5. Рассчитать текущую стоимость арендных платежей путем суммирования результата по периодам (PVn * Kdn)
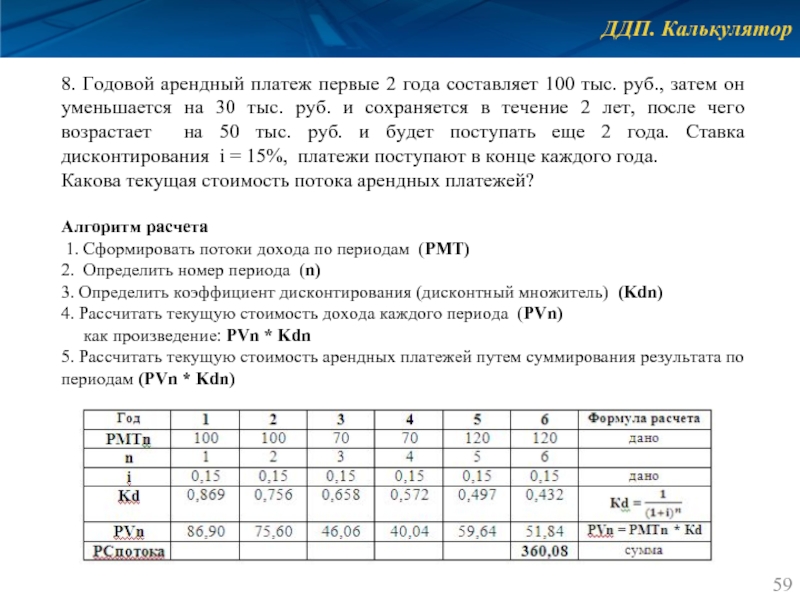
Слайд 59ДДП. Калькулятор
8. Годовой арендный платеж первые 2 года составляет 100 тыс.
Какова текущая стоимость потока арендных платежей?
Алгоритм расчета
1. Сформировать потоки дохода по периодам (РМТ)
2. Определить номер периода (n)
3. Определить коэффициент дисконтирования (дисконтный множитель) (Kdn)
4. Рассчитать текущую стоимость дохода каждого периода (PVn)
как произведение: PVn * Kdn
5. Рассчитать текущую стоимость арендных платежей путем суммирования результата по периодам (PVn * Kdn)
Слайд 60ДДП. Калькулятор
Порядок расчета:
2nd –CLRWork
CF0 = 0 ENTER[↓]
CO1 = 100
FO1 = 2 ENTER[↓]
CO2 = 70 ENTER[↓]
FO2=2 ENTER[↓]
CO3 = 120 ENTER[↓]
FO2=2 ENTER[↓]
NPV I =15 ENTER [↓]
CPT
NPV = 360,16
8. Годовой арендный платеж первые 2 года составляет 100 тыс. руб., затем он уменьшается на 30 тыс. руб. и сохраняется в течение 2 лет, после чего возрастает на 50 тыс. руб. и будет поступать еще 2 года. Ставка дисконтирования i = 15%, платежи поступают в конце каждого года.
Какова текущая стоимость потока арендных платежей?
Слайд 61ДДП. Калькулятор
9. Сданный в аренду производственный комплекс в течение 3 лет
Через 5 лет предполагается, что комплекс будет продан за 200 тыс. де.
За какую сумму целесообразно продать этот объект в настоящее время?
Алгоритм расчета
1. Сформировать потоки дохода по периодам – РМТn
Определить номер периода – n
Определить ставку дисконта (общая норма доходности) – i
Рассчитать дисконтный множитель – Kd
Рассчитать текущую стоимость по каждому периоду PVn и суммировать
Рассчитать текущую стоимость продажи объекта (реверсия) PVP
7. Рассчитать рыночную стоимость объекта в настоящее время путем суммирования потока доходов и стоимости реверсии.
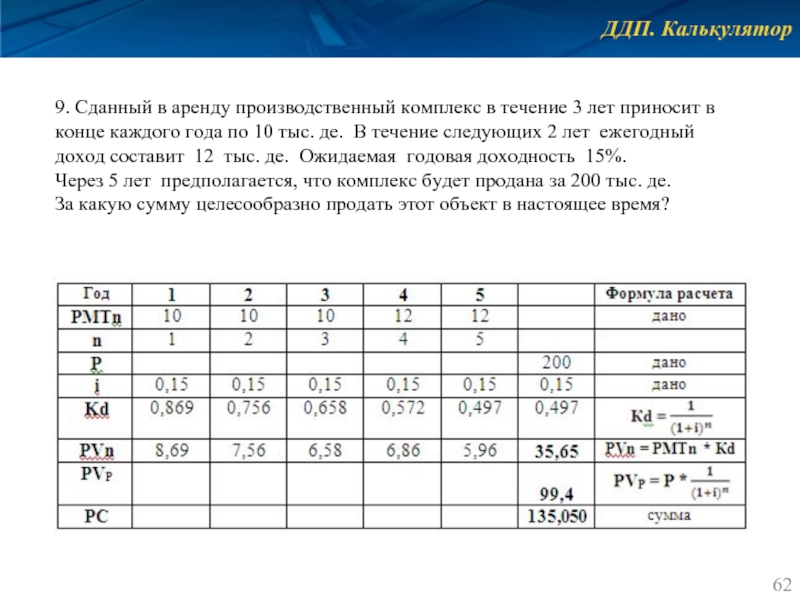
Слайд 62ДДП. Калькулятор
9. Сданный в аренду производственный комплекс в течение 3 лет
Через 5 лет предполагается, что комплекс будет продана за 200 тыс. де.
За какую сумму целесообразно продать этот объект в настоящее время?
Рыночная стоимость объекта составляет 135,050 тыс. де.
Слайд 63ДДП. Калькулятор
Порядок расчета:
ON/OFF
2nd –CLRWork
CF0 = 0 ENTER[↓]
CO1 = 10
FO1 = 3 ENTER[↓]
CO2 = 12 ENTER[↓]
FO2= 1 ENTER[↓]
CO3 = 212 ENTER[↓]
FO2= 1 ENTER[↓]
NPV I =15 ENTER [↓]
CPT
NPV = 135,09
9. Сданный в аренду производственный комплекс в течение 3 лет приносит в конце каждого года по 10 тыс. де. В течение следующих 2 лет ежегодный доход составит 12 тыс. де. Ожидаемая годовая доходность 15%.
Через 5 лет предполагается, что комплекс за 200 тыс. де. За какую сумму целесообразно продать этот объект в настоящее время?
Слайд 64EXSEL
ОБОЗНАЧЕНИЯ В EXSEL
1. Будущая стоимость единицы БС
4. Текущая стоимость единицы ПС (PV)
2. Будущая стоимость аннуитета БС (FV)
3. Фактор фонда возмещения ПЛТ (РМТ)
5. Текущая стоимость аннуитета ПС (PV)
6. Взнос за амортизацию единицы ПЛТ (PМТ)
Период – Кпер
Ставка - Ставка
Слайд 65EXSEL
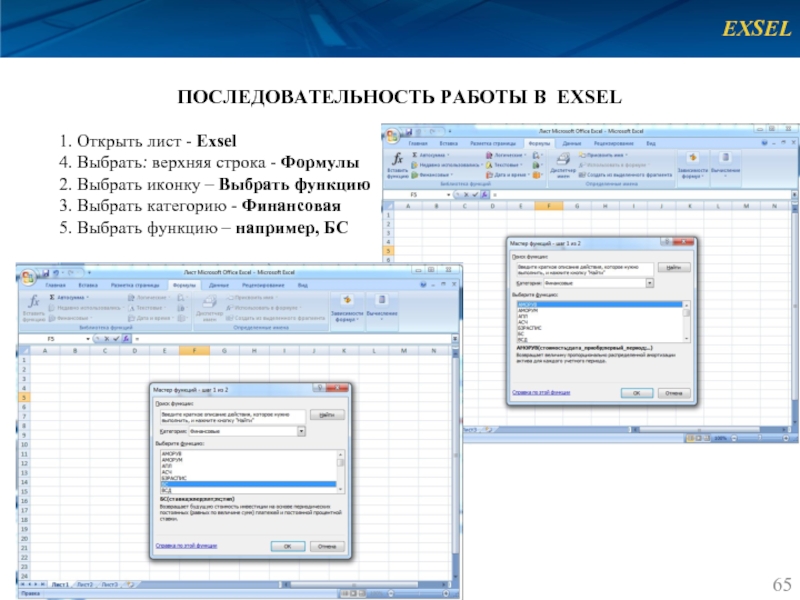
ПОСЛЕДОВАТЕЛЬНОСТЬ РАБОТЫ В EXSEL
1. Открыть лист - Exsel
2. Выбрать иконку – Выбрать функцию
3. Выбрать категорию - Финансовая
5. Выбрать функцию – например, БС
Слайд 66EXSEL
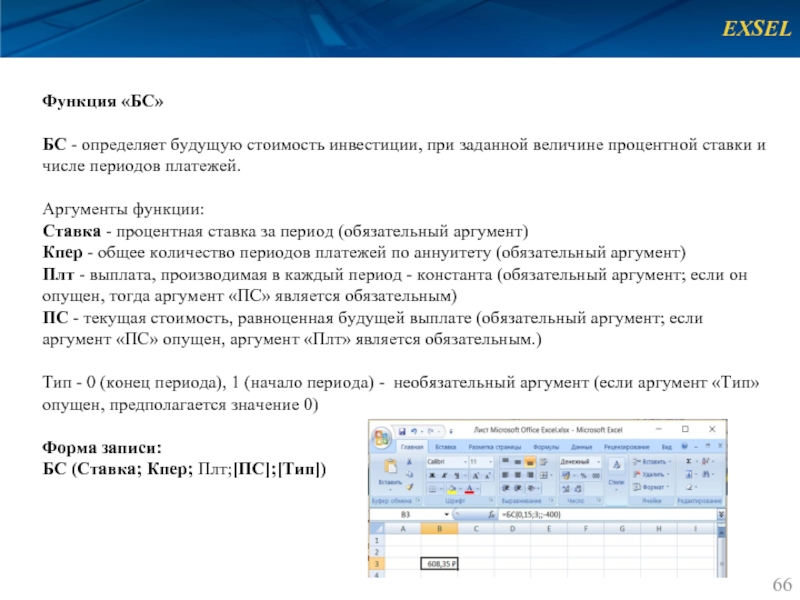
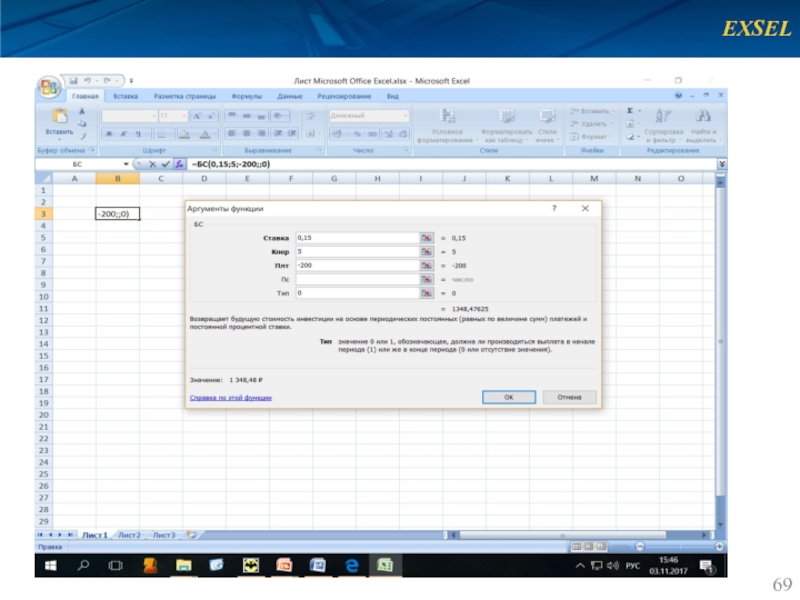
Функция «БС»
БС - определяет будущую стоимость инвестиции, при
Аргументы функции:
Ставка - процентная ставка за период (обязательный аргумент)
Кпер - общее количество периодов платежей по аннуитету (обязательный аргумент)
Плт - выплата, производимая в каждый период - константа (обязательный аргумент; если он опущен, тогда аргумент «ПС» является обязательным)
ПС - текущая стоимость, равноценная будущей выплате (обязательный аргумент; если аргумент «ПС» опущен, аргумент «Плт» является обязательным.)
Тип - 0 (конец периода), 1 (начало периода) - необязательный аргумент (если аргумент «Тип» опущен, предполагается значение 0)
Форма записи:
БС (Ставка; Кпер; Плт;[ПС];[Тип])
Слайд 67EXSEL
Функция «ПС»
ПС - возвращает приведенную (к текущему моменту)
Аргументы функции:
Ставка - процентная ставка за период (обязательный аргумент)
Кпер - общее количество периодов платежей по аннуитету (обязательный аргумент)
Плт - выплата, производимая в каждый период - константа (обязательный аргумент; если аргумент Плт опущен, тогда аргумент «ПС» является обязательным)
БС — значение будущей стоимости, т. е. желаемого остатка средств после последнего платежа (необязательный аргумент; если аргумент «БС» опущен, необходимо использовать аргумент "Плт"
Тип - 0 (конец периода), 1 (начало периода) - необязательный аргумент (если аргумент «Тип» опущен, предполагается значение 0)
Форма записи:
ПС (Ставка; Кпер; Плт;[Бс];[Тип])
Слайд 68EXSEL
Функция «ПЛТ»
ПЛТ возвращает сумму периодического платежа для аннуитета на
Аргументы функции:
Ставка - процентная ставка за период (обязательный аргумент)
Кпер - общее количество периодов платежей по аннуитету (обязательный аргумент)
ПС - приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей (обязательный аргумент; если аргумент ПС опущен, тогда аргумент «БС» является обязательным)
Тип - 0 (конец периода), 1 (начало периода). Необязательный аргумент (если аргумент "Тип" опущен, предполагается значение 0)
Форма записи:
ПЛТ (Ставка;Кпер;Пс;[Бс];[Тип])
Слайд 70EXSEL
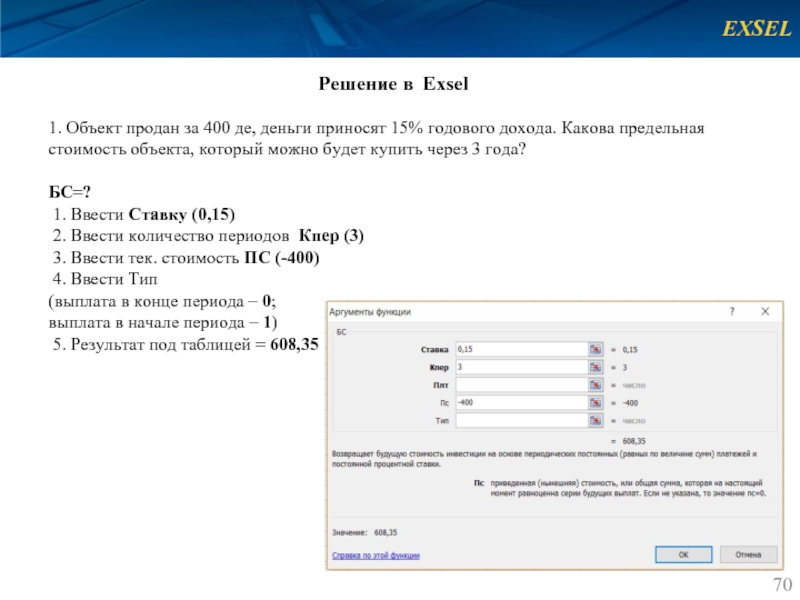
Решение в Exsel
1. Объект продан за 400 де, деньги приносят
БС=?
1. Ввести Ставку (0,15)
2. Ввести количество периодов Кпер (3)
3. Ввести тек. стоимость ПС (-400)
4. Ввести Тип
(выплата в конце периода – 0;
выплата в начале периода – 1)
5. Результат под таблицей = 608,35
Слайд 71EXSEL
Решение в Exsel
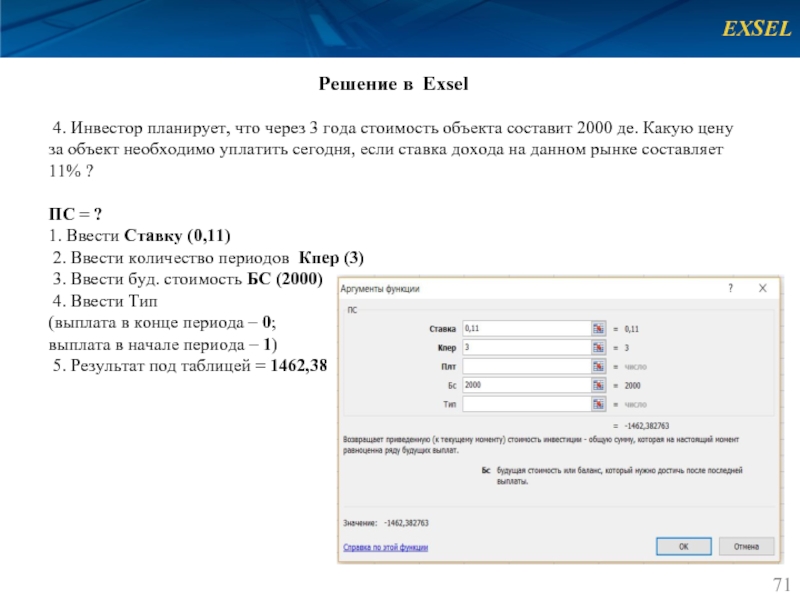
4. Инвестор планирует, что через 3 года
ПС = ?
1. Ввести Ставку (0,11)
2. Ввести количество периодов Кпер (3)
3. Ввести буд. стоимость БС (2000)
4. Ввести Тип
(выплата в конце периода – 0;
выплата в начале периода – 1)
5. Результат под таблицей = 1462,38
Слайд 72EXSEL
Решение в Exsel
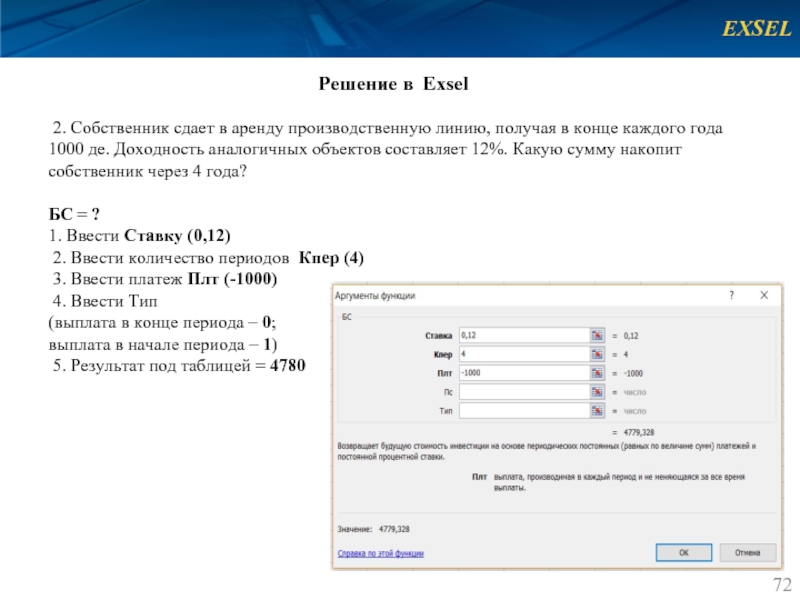
2. Собственник сдает в аренду производственную линию,
БС = ?
1. Ввести Ставку (0,12)
2. Ввести количество периодов Кпер (4)
3. Ввести платеж Плт (-1000)
4. Ввести Тип
(выплата в конце периода – 0;
выплата в начале периода – 1)
5. Результат под таблицей = 4780
Слайд 73EXSEL
Решение в Exsel
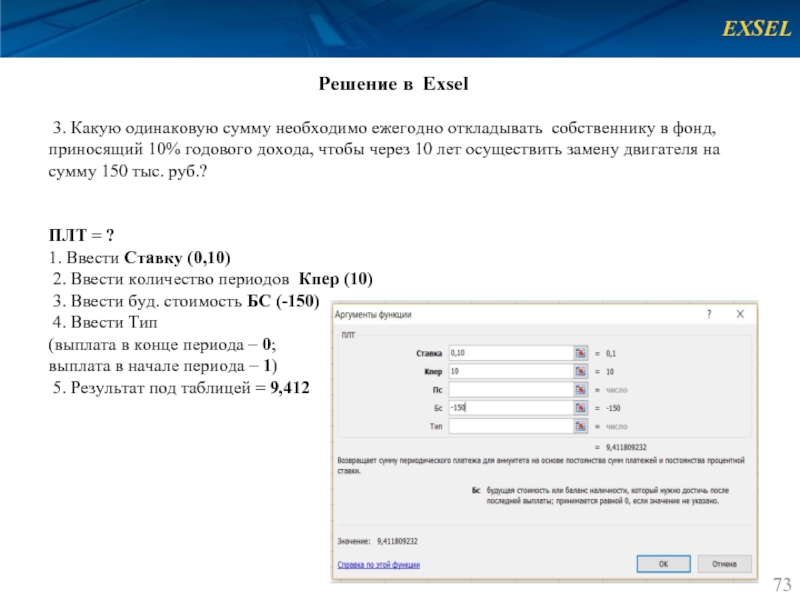
3. Какую одинаковую сумму необходимо ежегодно откладывать
ПЛТ = ?
1. Ввести Ставку (0,10)
2. Ввести количество периодов Кпер (10)
3. Ввести буд. стоимость БС (-150)
4. Ввести Тип
(выплата в конце периода – 0;
выплата в начале периода – 1)
5. Результат под таблицей = 9,412
Слайд 74EXSEL
Решение в Exsel
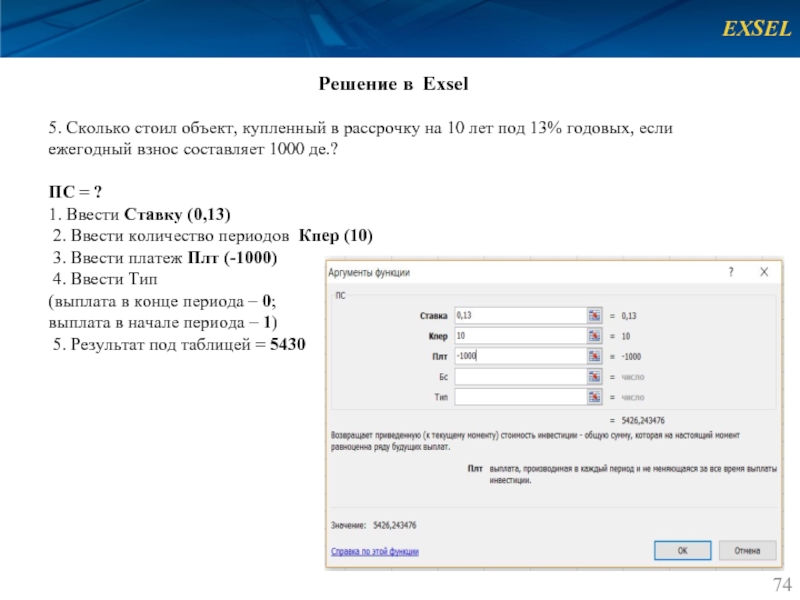
5. Сколько стоил объект, купленный в рассрочку на
ПС = ?
1. Ввести Ставку (0,13)
2. Ввести количество периодов Кпер (10)
3. Ввести платеж Плт (-1000)
4. Ввести Тип
(выплата в конце периода – 0;
выплата в начале периода – 1)
5. Результат под таблицей = 5430
Слайд 75EXSEL
Решение в Exsel
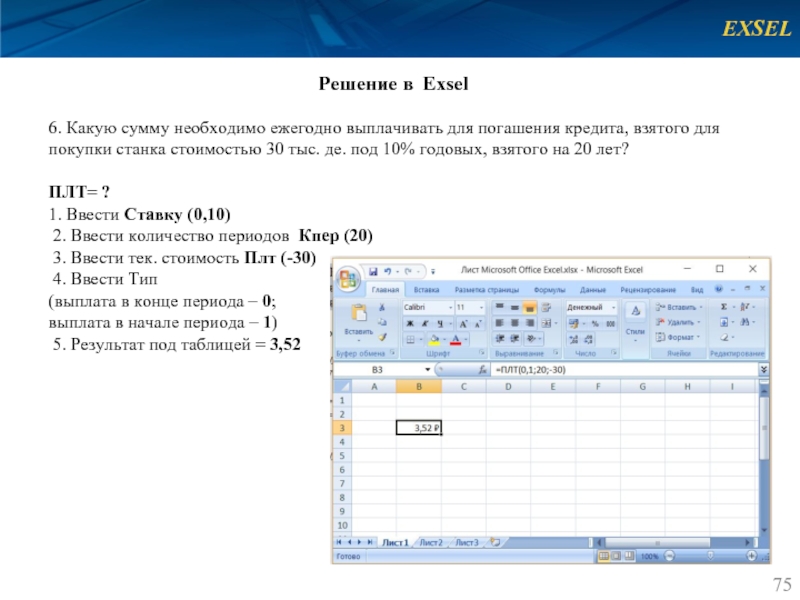
6. Какую сумму необходимо ежегодно выплачивать для погашения
ПЛТ= ?
1. Ввести Ставку (0,10)
2. Ввести количество периодов Кпер (20)
3. Ввести тек. стоимость Плт (-30)
4. Ввести Тип
(выплата в конце периода – 0;
выплата в начале периода – 1)
5. Результат под таблицей = 3,52
































![КалькуляторПодготовка калькулятора:ON/OFF2nd – RESETENTERCE/C2nd – FORMATDEC = 4,000 ENTER [↓] DEG ENTER [↓] US 12-31-19902nd](/img/tmb/1/12038/8356676d55b18ed8250ca703705f5fb9-800x.jpg)
![Финансовый калькуляторФорматирование[2nd][Format]](/img/tmb/1/12038/2d02c227948ab4b56e63cc046bd2a0e8-800x.jpg)














![ДДП. КалькуляторПорядок расчета:2nd –CLRWorkCF0 = 0 ENTER[↓]CO1 = 100 ENTER[↓]FO1 = 2 ENTER[↓]CO2 = 70](/img/tmb/1/12038/2e7f8fdd26886e36f1d1c0a0d5e349ef-800x.jpg)

![ДДП. КалькуляторПорядок расчета:ON/OFF2nd –CLRWorkCF0 = 0 ENTER[↓]CO1 = 10 ENTER[↓]FO1 = 3 ENTER[↓]CO2 = 12](/img/tmb/1/12038/31ae74d484f46186de43c7cfd28629aa-800x.jpg)