на основе теории ожидаемой полезности
Решение инвестора о покупке рискового актива: теорема о диверсификации
Парадоксы теории ожидаемой полезности в лабораторных и реальных условиях
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория выбора в условиях неопределенности - 3 презентация
Содержание
- 1. Теория выбора в условиях неопределенности - 3
- 2. В качестве еще одного примера применения теории
- 3. Нам будет удобнее сразу сформулировать задачу инвестора
- 4. Cиняя 45º линия соответствует доходам от портфелей,
- 5. Задача инвестора в терминах контингентных благ:
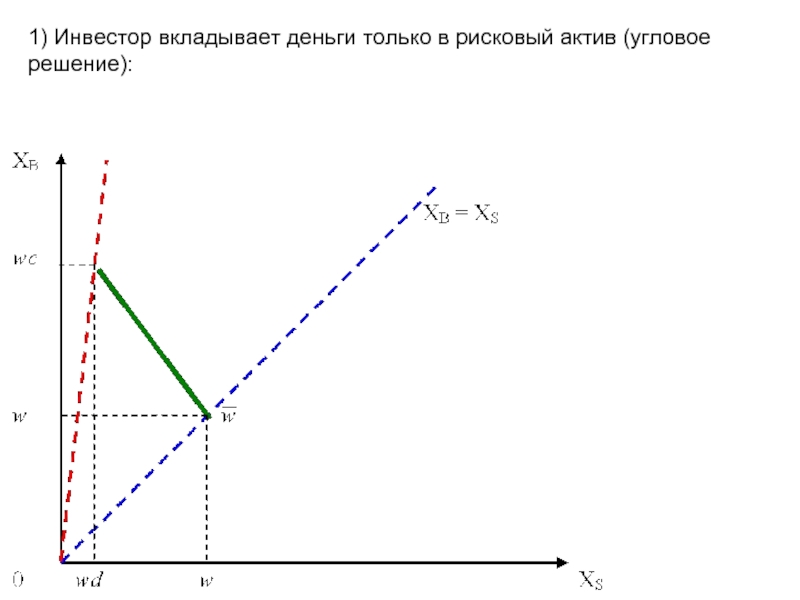
- 6. 1) Инвестор вкладывает деньги только в рисковый актив (угловое решение):
- 7. 2) Инвестор вкладывает часть денег в рисковый, а часть – в безрисковый актив (внутреннее решение)
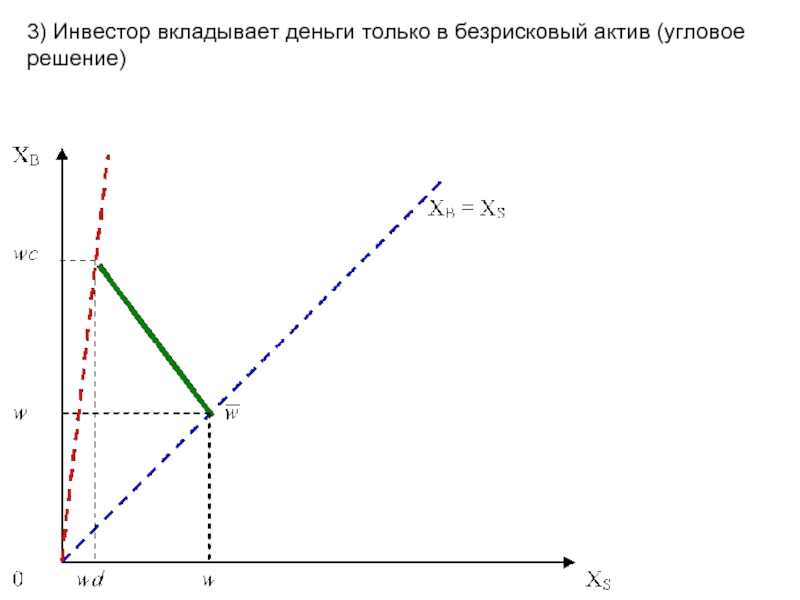
- 8. 3) Инвестор вкладывает деньги только в безрисковый актив (угловое решение)
- 9. Мы можем выяснить, при каких условиях инвестор-рискофоб
- 10. Итак, мы выяснили, что для случая с
- 11. Теорема о диверсификации Самуэльсона Пусть предпочтения инвестора-рискофоба
- 12. Парадоксы теории ожидаемой полезности Теория ожидаемой полезности
- 13. Парадокс Алле Первым парадоксом, привлекшим широкое внимание,
- 14. Парадокс «одинаковых вероятностей» Kahneman, Tversky, 1979:
- 15. «Обращение предпочтений»: эффект фрэйминга
- 16. Может показаться, что перечисленные парадоксы, обнаруженные преимущественно
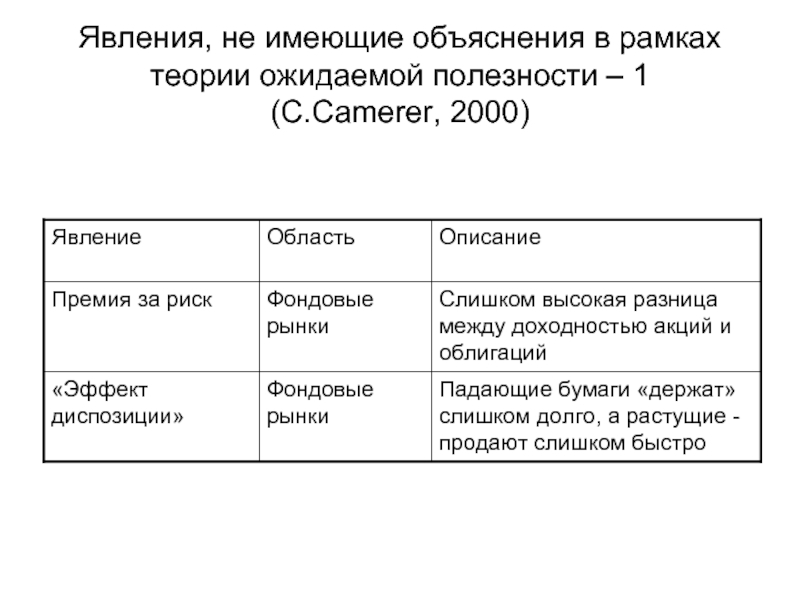
- 17. Явления, не имеющие объяснения в рамках теории ожидаемой полезности – 1 (C.Camerer, 2000)
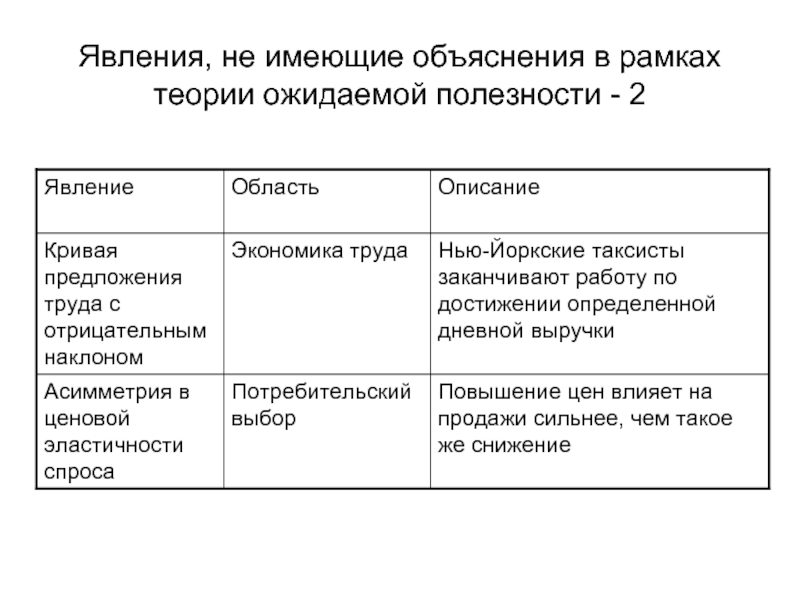
- 18. Явления, не имеющие объяснения в рамках теории ожидаемой полезности - 2
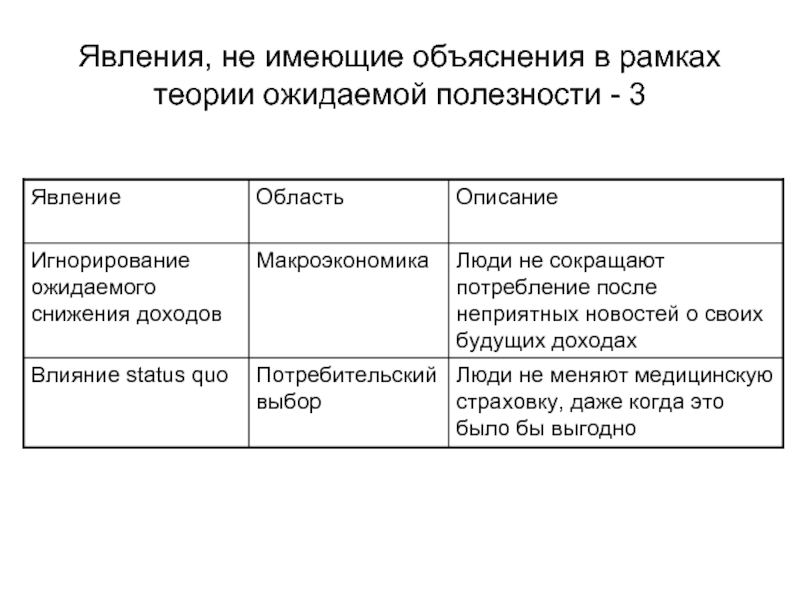
- 19. Явления, не имеющие объяснения в рамках теории ожидаемой полезности - 3
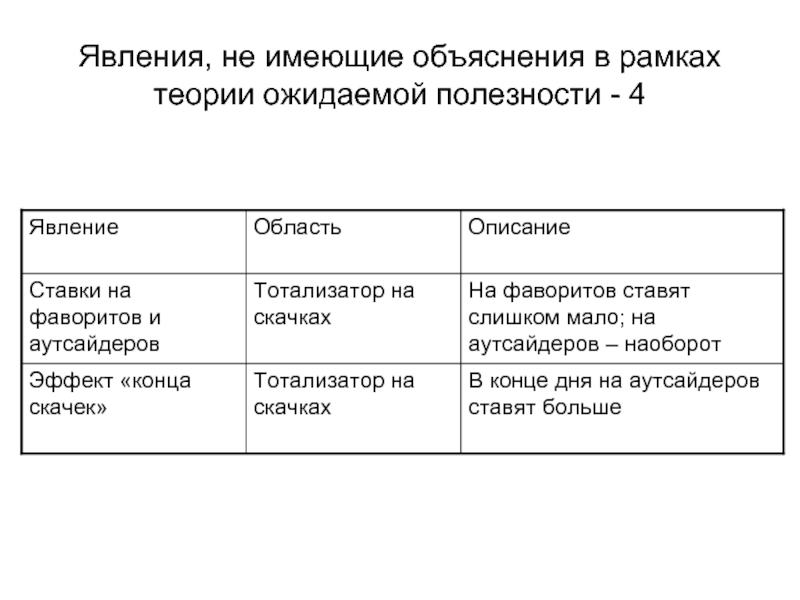
- 20. Явления, не имеющие объяснения в рамках теории ожидаемой полезности - 4
- 21. Явления, не имеющие объяснения в рамках теории ожидаемой полезности - 5
Слайд 2В качестве еще одного примера применения теории ожидаемой полезности, рассмотрим модель
инвестиций в рисковый актив
Предпосылки:
инвестор-рискофоб, предпочтения описываются функцией ожидаемой полезности фон Н.-М.,
возможны два состояния мира:
с вероятностью p ∈ (0; 1) наступает экономический рост (B)
с вероятностью (1 – p) наступает экономический кризис (S)
первоначальное богатство индивида составляет w
индивиду доступны 2 актива:
актив 1 (безрисковый): вложив а, вы получаете a в любом состоянии мира
актив 2 (рисковый): вложив a, вы получаете:
аc > a в состоянии мира B
аd < a в состоянии мира S
Как инвестор выберет свой оптимальный портфель?
Предпосылки:
инвестор-рискофоб, предпочтения описываются функцией ожидаемой полезности фон Н.-М.,
возможны два состояния мира:
с вероятностью p ∈ (0; 1) наступает экономический рост (B)
с вероятностью (1 – p) наступает экономический кризис (S)
первоначальное богатство индивида составляет w
индивиду доступны 2 актива:
актив 1 (безрисковый): вложив а, вы получаете a в любом состоянии мира
актив 2 (рисковый): вложив a, вы получаете:
аc > a в состоянии мира B
аd < a в состоянии мира S
Как инвестор выберет свой оптимальный портфель?
Слайд 3Нам будет удобнее сразу сформулировать задачу инвестора в терминах контингентных благ.
Их здесь два – XB (богатство в состоянии мира B) и XS (богатство в состоянии мира S).
Начнем с бюджетного ограничения. Предположим, инвестор вкладывает a долларов в рисковый актив. Тогда его бюджетное ограничение в терминах контингентных благ описывается системой:
Давайте посмотрим, как выглядит эта бюджетная линия в пространстве контингентных благ ➔
Начнем с бюджетного ограничения. Предположим, инвестор вкладывает a долларов в рисковый актив. Тогда его бюджетное ограничение в терминах контингентных благ описывается системой:
Давайте посмотрим, как выглядит эта бюджетная линия в пространстве контингентных благ ➔
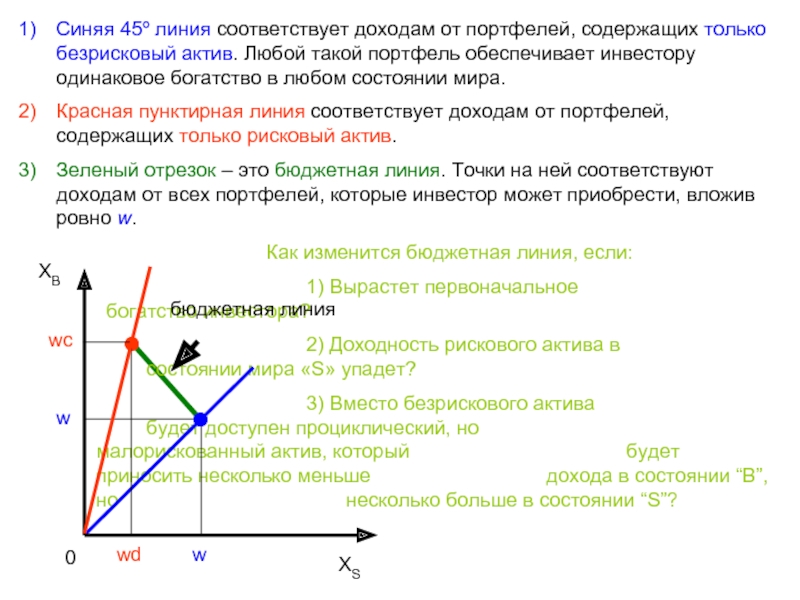
Слайд 4Cиняя 45º линия соответствует доходам от портфелей, содержащих только безрисковый актив.
Любой такой портфель обеспечивает инвестору одинаковое богатство в любом состоянии мира.
Красная пунктирная линия соответствует доходам от портфелей, содержащих только рисковый актив.
Зеленый отрезок – это бюджетная линия. Точки на ней соответствуют доходам от всех портфелей, которые инвестор может приобрести, вложив ровно w.
Как изменится бюджетная линия, если:
1) Вырастет первоначальное богатство инвестора?
2) Доходность рискового актива в состоянии мира «S» упадет?
3) Вместо безрискового актива будет доступен проциклический, но малорискованный актив, который будет приносить несколько меньше дохода в состоянии “B”, но несколько больше в состоянии “S”?
Красная пунктирная линия соответствует доходам от портфелей, содержащих только рисковый актив.
Зеленый отрезок – это бюджетная линия. Точки на ней соответствуют доходам от всех портфелей, которые инвестор может приобрести, вложив ровно w.
Как изменится бюджетная линия, если:
1) Вырастет первоначальное богатство инвестора?
2) Доходность рискового актива в состоянии мира «S» упадет?
3) Вместо безрискового актива будет доступен проциклический, но малорискованный актив, который будет приносить несколько меньше дохода в состоянии “B”, но несколько больше в состоянии “S”?
0
XS
XB
wc
w
wd
w
бюджетная линия
Слайд 5Задача инвестора в терминах контингентных благ:
Учитывая монотонность и строгую вогнутость функции
ожидаемой полезности, у этой задачи может быть 3 типа решений ➔
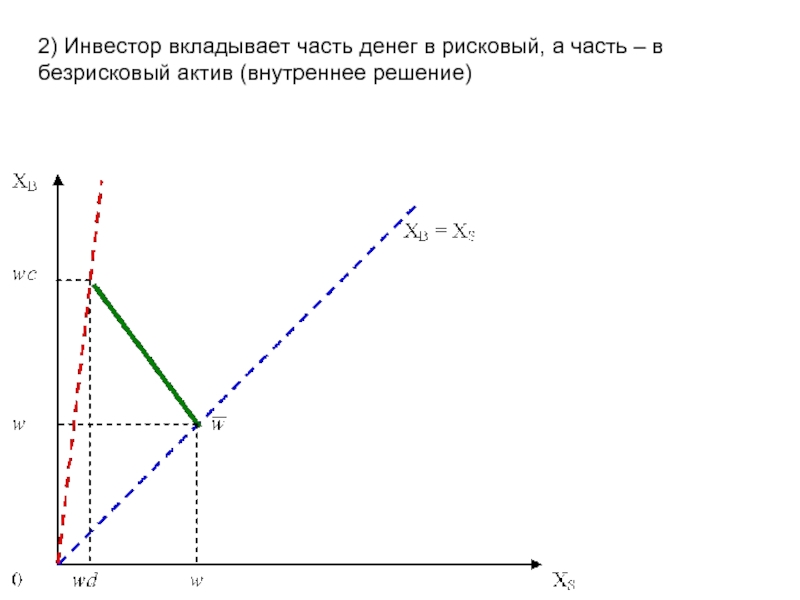
Слайд 72) Инвестор вкладывает часть денег в рисковый, а часть – в
безрисковый актив (внутреннее решение)
Слайд 9Мы можем выяснить, при каких условиях инвестор-рискофоб вкладывает хоть что-нибудь в
рисковый актив?
Как подсказывает график слева, чтобы инвестор вкладывал хоть что-то в рисковый актив, |MRSXSXB| в точке (w, w) должна быть меньше модуля тангенса угла наклона бюджетной линии:
Это неравенство можно преобразовать к следующему виду:
➔ ожидаемый доход на $1, вложенный в рисковый актив должен превышать таковой для безрискового актива!
Как подсказывает график слева, чтобы инвестор вкладывал хоть что-то в рисковый актив, |MRSXSXB| в точке (w, w) должна быть меньше модуля тангенса угла наклона бюджетной линии:
Это неравенство можно преобразовать к следующему виду:
➔ ожидаемый доход на $1, вложенный в рисковый актив должен превышать таковой для безрискового актива!
Слайд 10Итак, мы выяснили, что для случая с двумя активами: рисковым и
безрисковым, рисковый актив обязательно войдет в оптимальный портфель, если его ожидаемая доходность выше доходности безрискового актива.
Этот результат является частным случаем Теоремы Самуэльсона о диверсификации портфеля ➔
Этот результат является частным случаем Теоремы Самуэльсона о диверсификации портфеля ➔
Слайд 11Теорема о диверсификации Самуэльсона
Пусть предпочтения инвестора-рискофоба описываются функцией ожидаемой полезности фон
Неймана—Моргенштерна с дважды дифференцируемой элементарной функцией полезности v(·), и кроме того:
доходности доступных ему активов статистически независимы;
инвестор может брать кредит по безрисковой ставке;
выполнены условия регулярности, обеспечивающие, что производная математического ожидания равна математическому ожиданию производной.
➔ Тогда любой актив, ожидаемая доходность которого выше доходности безрискового актива, войдет в портфель.
доходности доступных ему активов статистически независимы;
инвестор может брать кредит по безрисковой ставке;
выполнены условия регулярности, обеспечивающие, что производная математического ожидания равна математическому ожиданию производной.
➔ Тогда любой актив, ожидаемая доходность которого выше доходности безрискового актива, войдет в портфель.
Слайд 12Парадоксы теории ожидаемой полезности
Теория ожидаемой полезности и представление о рискофобии как
основном типе отношения к риску долго была (и, пожалуй, до сих пор остается!) доминирующей парадигмой в области экономического анализа выбора в условиях неопределенности.
Однако, уже c середины XX века исследователи стали замечать, что в своем классическом виде (с элементарной функцией полезности, не зависимой от состояний мира, с линейностью по вероятностям…) теория ожидаемой полезности не позволяет объяснить ряд парадоксов, устойчиво проявляющихся в поведении людей ➔
Однако, уже c середины XX века исследователи стали замечать, что в своем классическом виде (с элементарной функцией полезности, не зависимой от состояний мира, с линейностью по вероятностям…) теория ожидаемой полезности не позволяет объяснить ряд парадоксов, устойчиво проявляющихся в поведении людей ➔
Слайд 13Парадокс Алле
Первым парадоксом, привлекшим широкое внимание, стал т.н. «парадокс Алле» (1953)
A
предпочиталось B, но D предпочиталось С – вопреки аксиоме независимости
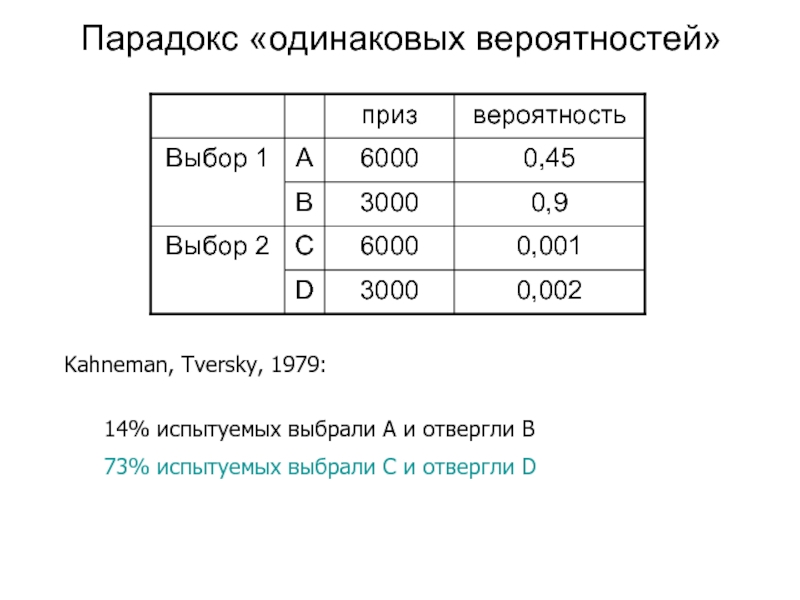
Слайд 14Парадокс «одинаковых вероятностей»
Kahneman, Tversky, 1979:
14% испытуемых выбрали А и отвергли
B
73% испытуемых выбрали C и отвергли D
73% испытуемых выбрали C и отвергли D
Слайд 15«Обращение предпочтений»: эффект фрэйминга
«Обращение предпочтений»: даже при одинаковых
выигрышах и одинаковых вероятностях, предпочтения могут меняться на противоположные в зависимости от постановки вопроса!
Известный пример: «азиатская болезнь» (Tversky & Kahneman, 1981). Поселок в 600 человек, опасность эпидемии. Варианты действий:
A) гарантированно спасти 200 человек
B) спасти 600 человек с вероятностью 1/3 (в случае неудачи умрут все)
Большинство предпочитало «А»
C) 400 человек обречены
D) с вероятностью 2/3 умрут все, с вероятностью 1/3 все выживут
Большинство предпочитало «D»
Известный пример: «азиатская болезнь» (Tversky & Kahneman, 1981). Поселок в 600 человек, опасность эпидемии. Варианты действий:
A) гарантированно спасти 200 человек
B) спасти 600 человек с вероятностью 1/3 (в случае неудачи умрут все)
Большинство предпочитало «А»
C) 400 человек обречены
D) с вероятностью 2/3 умрут все, с вероятностью 1/3 все выживут
Большинство предпочитало «D»
Слайд 16 Может показаться, что перечисленные парадоксы, обнаруженные преимущественно в лабораторных условиях, имеют
мало отношения к экономическому выбору реальных людей.
Но и вне лабораторных экспериментов можно найти достаточно случаев, не объяснимых в рамках теории ожидаемой полезности в ее классическом виде!
Вот какой перечень аномалий приводит, например, Колин Камерер, известный американский экономист, специализирующийся в области поведенческой экономики в своей статье Prospect Theory in the Wild: Evidence from the field (2000)* ➔
* Точная ссылка: Prospect Theory in the Wild: Evidence from the field (2000) //D.Kahneman, A.Tversky (eds.) Choices, Values and Frames NY: CUP and the Russell Sage Foundation, 288-300
Но и вне лабораторных экспериментов можно найти достаточно случаев, не объяснимых в рамках теории ожидаемой полезности в ее классическом виде!
Вот какой перечень аномалий приводит, например, Колин Камерер, известный американский экономист, специализирующийся в области поведенческой экономики в своей статье Prospect Theory in the Wild: Evidence from the field (2000)* ➔
* Точная ссылка: Prospect Theory in the Wild: Evidence from the field (2000) //D.Kahneman, A.Tversky (eds.) Choices, Values and Frames NY: CUP and the Russell Sage Foundation, 288-300