ФИНАНСОВЫХ РЕШЕНИЙ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 3. Портфельный анализ. История теории финансового портфеля презентация
Содержание
- 1. Тема 3. Портфельный анализ. История теории финансового портфеля
- 2. Тема 3. Портфельный анализ
- 3. История теории финансового портфеля Начало современной
- 4. Основные количественные характеристики отдельной рисковой ценной бумаги
- 5. Доходность акции (финансового инструмента) Доходность ri-процентное
- 6. Математическое ожидание - mi и дисперсия –
- 7. Ковариация и корреляция между доходностями двух ценных
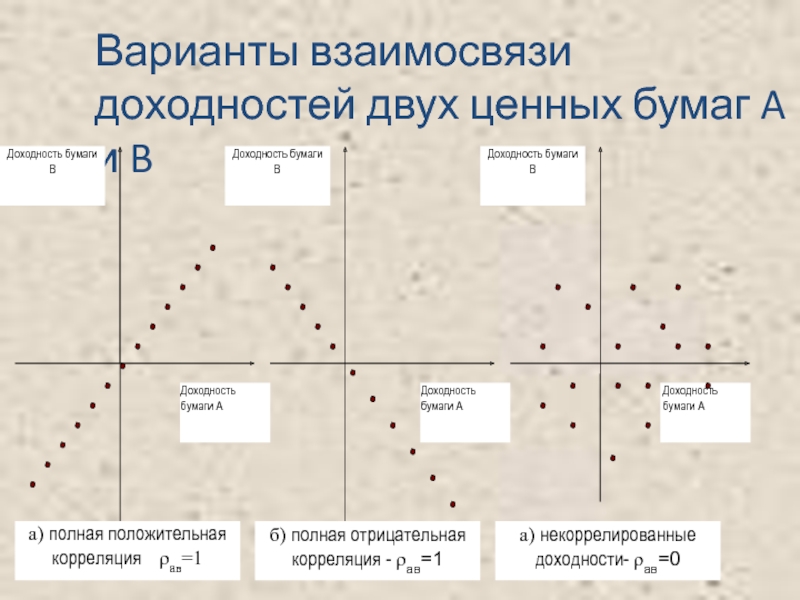
- 8. Варианты взаимосвязи доходностей двух ценных бумаг A и B
- 9. Правила доминирования рационального инвестора 1. Если
- 10. Задача 1. Рассматриваются три равновероятных состояния экономики
- 12. Задачи формирования портфелей ценных бумаг Портфель –
- 13. Задачи формирования портфелей ценных бумаг Портфель
- 14. Основные характеристики портфеля ЦБ mp
- 15. Риск
- 16. Ковариационная матрица порядка-N Ковариация -
- 17. ПРИМЕР 1. Некоррелированнные ЦБ Предположим ,
- 18. Предположим, что деньги вложены равными долями во
- 19. ПРИМЕР. Инвестор может составить портфель из 4 видов ценных бумаг:
- 20. Рассмотрим несколько вариантов составления портфеля равными долями.
- 21. 2. Портфель состоит из бумаг 1, 2 и 3 вида.
- 22. 3. Портфель состоит из бумаг всех видов. Эффективность портфеля растет быстрее, чем его риск.
- 23. Для некоррелированных ЦБ, если их число n
- 24. Диверсификация Диверсификация (разнообразие ценных бумаг в
- 25. 2. Влияние корреляции ЦБ разного
- 26. Рассмотрим коэффициент корреляции: Рассмотрим два крайних случая:
- 27. 2.1. Полная прямая корреляция Это значит,
- 28. Если деньги вложить равными долями ,то
- 29. Заметим, что положительная корреляция между эффективностями ЦБ
- 30. 2.2. Полная обратная корреляция Пусть n=2:
- 31. Если То Таким образом, при
- 32. Эффективный набор портфелей из 2-х бумаг
- 33. Эффективный инвестиционный портфель Эффективный портфель – это
- 34. Эффективное множество для произвольного количества ЦБ Наилучшими
- 35. Модели оптимального портфеля Задача оптимизации
- 36. 1. Модель Марковица Модель Марковица рассматривает в
- 37. Модели портфеля ценных бумаг Портфель называют стандартным,
- 38. Модели портфеля ценных бумаг Оптимальное
- 39. Операция «short sale» Инвестор, формирующий портфель, обязуется
- 40. В модели Марковица обычно рассматриваются два типа
- 41. 1.Портфель Марковица минимального риска. Найти вектор
- 42. Пример Сформировать портфель минимального риска из
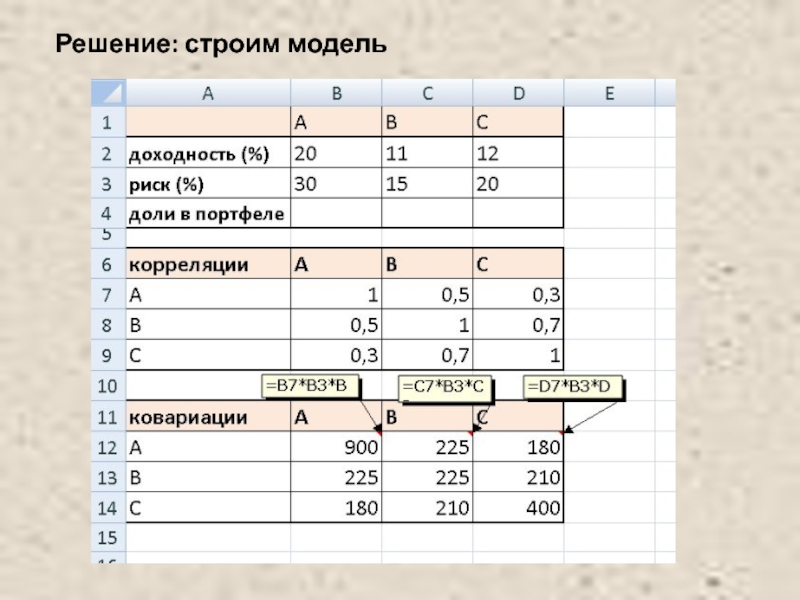
- 43. Решение: строим модель
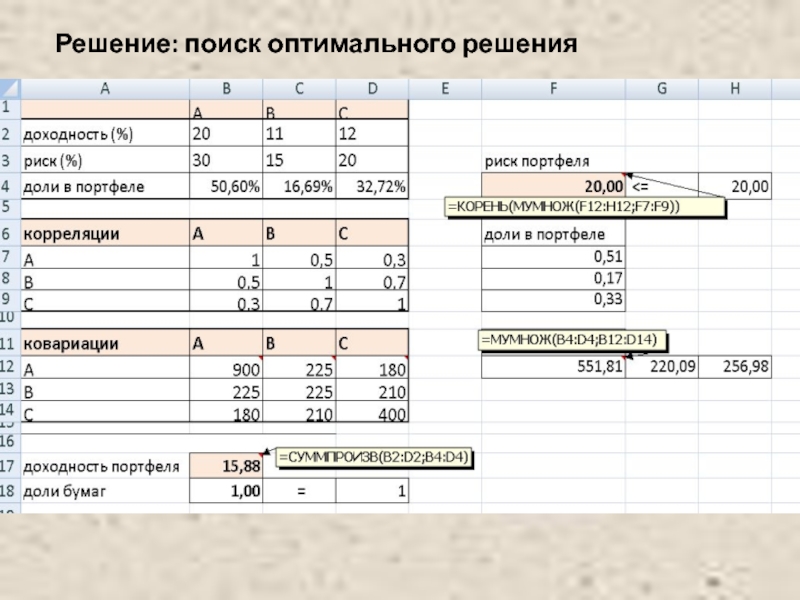
- 44. Решение: поиск оптимального решения
- 45. 2.Портфель Марковица максимальной эффективности. Найти вектор
- 46. Пример.
- 48. Решение: строим модель
- 49. Решение: поиск оптимального решения
- 51. Безрисковый актив Безрисковый актив имеет, по
- 52. Есть только один тип казначейских бумаг, удовлетворяющих
- 53. Безрисковое заимствование. Пусть инвестор не ограничен
- 55. Модель Тобина-Шарпа-Литнера (D. Tobin –лауреат
- 56. Модель Тобина-Шарпа-Литнера для 2-х бумаг. Считается,
- 57. Модель Тобина-Шарпа-Литнера Эффективность портфеля линейно зависит от его риска:
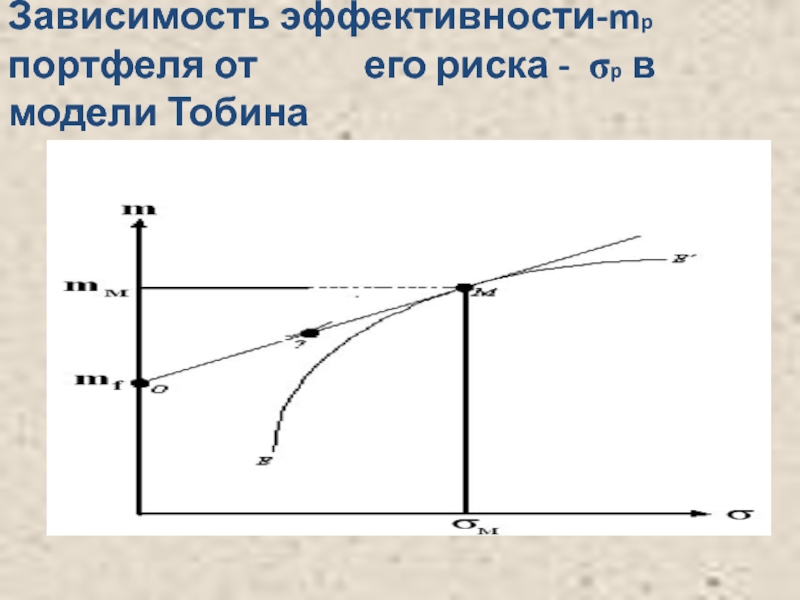
- 58. Зависимость эффективности-mp портфеля от его риска - σp в модели Тобина
- 59. 3.Модель Тобина c n рисковыми бумагами.
- 60. Заимствование и инвестирование в рискованные
- 61. Можно показать, что любая комбинация заимствования и
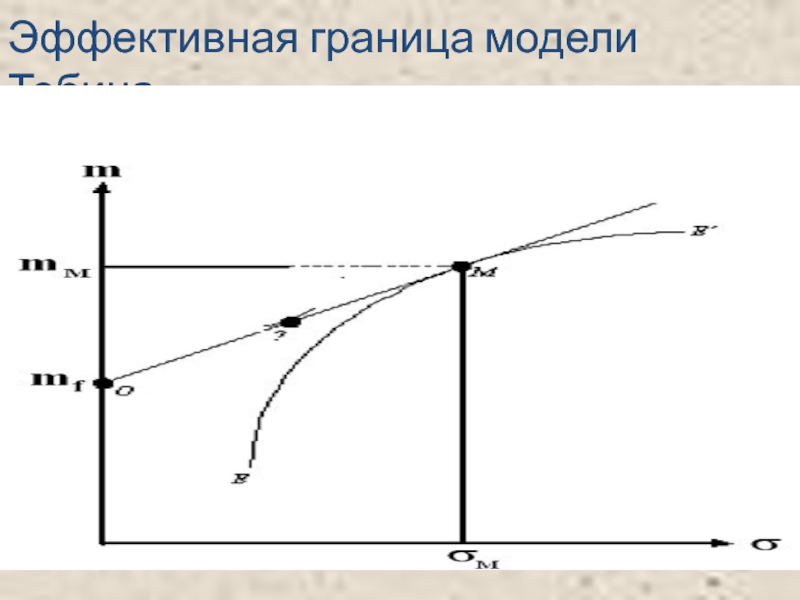
- 62. Эффективная граница модели Тобина
- 64. Если возможно безрисковое заимствование и кредитование, то
- 67. Предоставляемые рынком возможности по выбору желаемой комбинации
- 68. Модель Марковица представляет собой задачу выбора эффективного
- 69. СПАСИБО ЗА ВНИМАНИЕ !
Тема 3. Портфельный анализ
Слайд 1Финансовый Университет при Правительстве РФ
Кафедра «Прикладная математика».
Угрозов Валерий Вячеславович
МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
Слайд 3История теории финансового портфеля
Начало современной теории финансового портфеля было заложено
в статье Гарри Марковица «Выбор портфеля» (1952). В этой статье была предложена математическая модель формирования оптимального портфеля ценных бумаг и были приведены методы построения таких портфелей при определенных условиях.
Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965), и было основано на понятиях систематического (рыночного) и несистематического рисков ценной бумаги.
Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965), и было основано на понятиях систематического (рыночного) и несистематического рисков ценной бумаги.
Слайд 4Основные количественные характеристики отдельной рисковой ценной бумаги
При формировании оптимального портфеля
ценных бумаг необходимы рыночные данные по отдельным ценным бумагам, информация о которых представлена на многочисленных информационных сайтах. Например, многие известные рыночные данные по значениям индексов и котирования многочисленных акций представлены на сайте http://www.finam.ru/analysis/.
Слайд 5Доходность акции (финансового инструмента)
Доходность ri-процентное изменение стоимости инвестиции в финансовые
активы за определенный период времени
где Сt – цена закрытия акции ( финансового инструмента) за данный месяц, Сt-1 – цена закрытия акции ( финансового инструмента) за предыдущий месяц .
mit – является случайной величиной , i-вид бумаги, t-время.
где Сt – цена закрытия акции ( финансового инструмента) за данный месяц, Сt-1 – цена закрытия акции ( финансового инструмента) за предыдущий месяц .
mit – является случайной величиной , i-вид бумаги, t-время.
Слайд 6Математическое ожидание - mi и дисперсия – σ2i доходности
ценной бумаги
pk- состояние экономики, k –число возможных состояний экономики, - среднее квадратическое отклонение, определяющая риск ценной бумаги
Слайд 7Ковариация и корреляция между доходностями двух ценных бумаг –A и B
Ковариация-
Корреляция
-,
Коэффициент вариации доходности -
Коэффициент вариации доходности -
Слайд 9Правила доминирования рационального инвестора
1. Если m1 = m2 и σ1
то первый вид ценных бумаг предпочтительнее, поскольку с ним связана меньшая степень риска.
2. Если σ1=σ2, а m1 > m2 , то целесообразно вложить деньги в 1-й вид ценных бумаг.
3. Если m1 > m2 и σ1>σ2 или m1 < m2 и σ1<σ2 , то целесообразно использовать коэффициент вариации доходности - С
Однако в зависимости от индивидуальной склонности к риску инвестор может предпочесть вариант с большей ожидаемой доходностью, но связанной и с большим риском, либо вариант с меньшей ожидаемой доходностью, но менее рискованный.
2. Если σ1=σ2, а m1 > m2 , то целесообразно вложить деньги в 1-й вид ценных бумаг.
3. Если m1 > m2 и σ1>σ2 или m1 < m2 и σ1<σ2 , то целесообразно использовать коэффициент вариации доходности - С
Однако в зависимости от индивидуальной склонности к риску инвестор может предпочесть вариант с большей ожидаемой доходностью, но связанной и с большим риском, либо вариант с меньшей ожидаемой доходностью, но менее рискованный.
Слайд 10Задача 1. Рассматриваются три равновероятных состояния экономики S1,S2,S3 , т.е. каждое
состояние может реализоваться с одинаковой вероятностью pk = 1/ 3 , k = 1,2,3. Значения доходностей ценных бумаг двух компаний A и B для каждого состояния k приводятся в табл. (в процентах).
Определить :1.Ожидаемое значение доходностей ценных бумаг каждой компании ; 2. Риск, связанный с вложением в каждую ценную бумагу; 3.Степень зависимости доходностей ценных бумаг компаний А и В.
Слайд 12Задачи формирования портфелей ценных бумаг
Портфель – это совокупность различных инвестиционных инструментов,
которые собраны воедино для достижения конкретной инвестиционной цели вкладчика.
Основы теории выбора портфеля впервые были разработаны нобелевским лауреатом Гарри Марковицем в статье «Выбор портфеля», опубликованной в 1952 г. Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965), и было основано на понятиях систематического (рыночного) и несистематического рисков ценной бумаги.
Основы теории выбора портфеля впервые были разработаны нобелевским лауреатом Гарри Марковицем в статье «Выбор портфеля», опубликованной в 1952 г. Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965), и было основано на понятиях систематического (рыночного) и несистематического рисков ценной бумаги.
Слайд 13Задачи формирования портфелей ценных бумаг
Портфель (инвестиционный портфель) - совокупность инвестиционных инструментов.
Главная
цель в формировании портфеля – достижение оптимального сочетания между риском и доходностью за счет набора инвестиционных инструментов, который должен обеспечить:
минимум риска потерь при заданном уровне доходности;
или максимальную доходность при заданном уровне риска.
минимум риска потерь при заданном уровне доходности;
или максимальную доходность при заданном уровне риска.
Слайд 14 Основные характеристики портфеля ЦБ
mp - доходность ( эффективность)портфеля ценных бумаг.
Данный параметр рассчитывается как взвешенная средняя из ожидаемых доходностей по каждой из ЦБ
где xi - доли инвестиций, помещенных в каждый из видов активов (эти доли называют портфельными весами), k – вид актива. XT=(х1, х2, … хn); mk - ожидаемая доходность по каждому виду активов.
Слайд 15 Риск портфеля
Риск портфеля -
σp - стандартное отклонение ставок дохода по портфелю, рассчитывается как квадратный корень из дисперсии портфельного дохода (вариации Vp),
- ковариационная матрица порядка N.
Слайд 16 Ковариационная матрица порядка-N
Ковариация - это статистическая мера взаимодействия случайных
переменных, например, доходности трех ценных бумаг.
Коэффициент корреляции между двумя переменными i и j можно рассчитать по выражению
Слайд 17ПРИМЕР
1. Некоррелированнные ЦБ
Предположим , что ЦБ различных видов ведут себя
независимо, т.е. они некоррелированы:
Тогда
Слайд 18Предположим, что деньги вложены равными долями во все виды ЦБ:
Тогда средняя
ожидаемая доходность портфеля:
Риск портфеля:
Слайд 20Рассмотрим несколько вариантов составления портфеля равными долями.
1. Портфель состоит из бумаг
1 и 2 вида.
Слайд 223. Портфель состоит из бумаг всех видов.
Эффективность портфеля растет быстрее, чем
его риск.
Слайд 23Для некоррелированных ЦБ, если их
число n в портфеле растет, то
риск будет
ограничен и он будет
стремиться к нулю при
Уменьшение риска
портфеля за счет увеличения в нем
числа ЦБ , получил название
эффекта диверсификации.
стремиться к нулю при
Уменьшение риска
портфеля за счет увеличения в нем
числа ЦБ , получил название
эффекта диверсификации.
Слайд 24Диверсификация
Диверсификация (разнообразие ценных бумаг в портфеле) приводит к снижению общего
риска портфеля. Это происходит вследствие сокращения собственного риска портфеля, в то время как рыночный риск портфеля остается приблизительно таким же. Этот же эффект воплощен в народной мудрости – «не клади все яйца в одну корзину». Принцип диверсификации гласит, что нужно проводить разнообразные, не связанные друг с другом операции, тогда эффективность окажется усредненной, а риск уменьшится.
Слайд 252. Влияние корреляции
ЦБ разного вида
Оценим влияние корреляции ЦБ.
Корреляция
не влияет на эффективность портфеля, поскольку
Но она будет влиять на риск:
Слайд 272.1. Полная прямая корреляция
Это значит, что при изменении i –го фактора
j – ый меняется прямо пропорционально.
Пусть n =2:
Пусть n =2:
Слайд 28Если деньги вложить равными долями ,то
и риск портфеля составит
Однако, в
этом случае диверсификация портфеля не дает эффекта – риск портфеля не будет стремиться к нулю при
Слайд 29Заметим, что положительная корреляция между эффективностями ЦБ имеет место, когда их
курс определяется одним фактором.
Например, цены акций электрических и транспортных компаний пропорциональны цене на нефть.
Диверсификация путем покупки и тех и других акций бесполезна – риск портфеля оказывается приблизительно таким же, как и среднеквадратичное отклонение цены на нефть.
Например, цены акций электрических и транспортных компаний пропорциональны цене на нефть.
Диверсификация путем покупки и тех и других акций бесполезна – риск портфеля оказывается приблизительно таким же, как и среднеквадратичное отклонение цены на нефть.
Слайд 31Если
То
Таким образом, при обратной корреляции возможно такое распределение вложений,
при которой риск полностью отсутствует.
Слайд 33Эффективный инвестиционный портфель
Эффективный портфель – это портфель подверженных риску ценных бумаг
(активов), дающий максимальный средний доход из всех портфелей с одинаковой дисперсией.
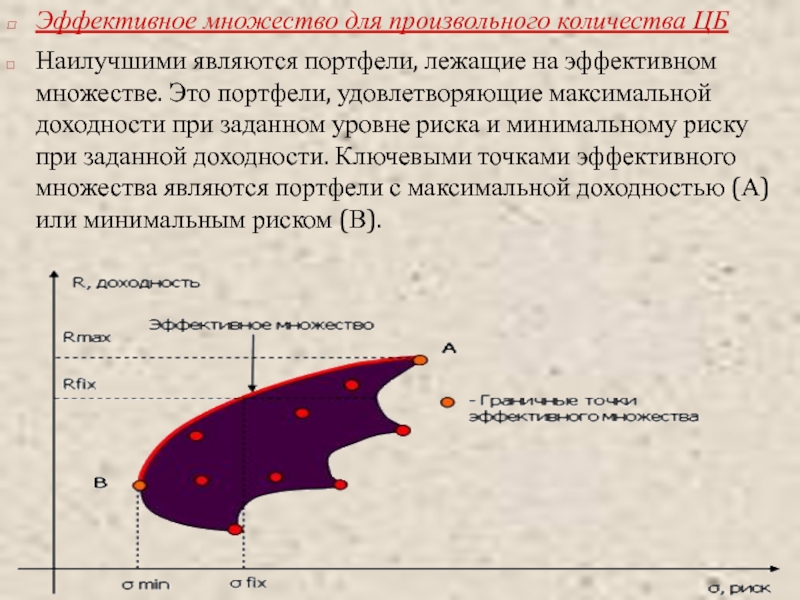
Слайд 34Эффективное множество для произвольного количества ЦБ
Наилучшими являются портфели, лежащие на эффективном
множестве. Это портфели, удовлетворяющие максимальной доходности при заданном уровне риска и минимальному риску при заданной доходности. Ключевыми точками эффективного множества являются портфели с максимальной доходностью (А) или минимальным риском (В).
Слайд 35Модели оптимального портфеля
Задача оптимизации сводится к определению такой структуры состава
портфеля(т.е. x1,x2,… инвестиций, чтобы величина ожидаемого дохода – mp и - уровень риска соответствовали целям инвесторов.
При этом целевой функцией может быть минимизация риска при заданной доходности, либо максимизация дохода при риске не выше заданного, a на компоненты вектора X, представляющего состав портфеля могут накладываться различные ограничения, зависящие от вида сделки, типа участвующих активов, величины открываемых позиций и т. д.
При этом целевой функцией может быть минимизация риска при заданной доходности, либо максимизация дохода при риске не выше заданного, a на компоненты вектора X, представляющего состав портфеля могут накладываться различные ограничения, зависящие от вида сделки, типа участвующих активов, величины открываемых позиций и т. д.
Слайд 361. Модель Марковица
Модель Марковица рассматривает в качестве допустимых только стандартные портфели
(без коротких позиций). Это значит, что на вектор Х накладываются два ограничения: основное
и неотрицательности xi ≥ 0 для всех i.
и неотрицательности xi ≥ 0 для всех i.
Слайд 37Модели портфеля ценных бумаг
Портфель называют стандартным, если инвестор по каждому активу
находится в длинной (long) позиции. Длинная позиция – это обычно покупка актива с намерением его последующей продажи (закрытие позиций).
Особенностью модели Марковица является то, что доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.
Особенностью модели Марковица является то, что доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.
Слайд 38Модели портфеля ценных бумаг
Оптимальное решение этой задачи обозначим значком
*. Если , то это означает рекомендацию вложить долю наличного капитала в ценные бумаги i-ro вида. Если же
, то содержательно это означает провести операцию «short sale» («короткая продажа»).
, то содержательно это означает провести операцию «short sale» («короткая продажа»).
Слайд 39Операция «short sale»
Инвестор, формирующий портфель, обязуется через какое-то время поставить ценные
бумаги i-го вида (вместе с доходом, какой они принесли бы их владельцу за это время). За это сейчас он получает их денежный эквивалент. Эти деньги он присоединяет к своему капиталу и покупает рекомендуемые оптимальным решением ценные бумаги. Так как ценные бумаги других видов (т.е. не i-ro вида) более эффективны, то инвестор оказывается в выигрыше. Можно обойтись и без операции «short sale», если инвестору доступны займы денежных средств по безрисковой ставке.
Слайд 40В модели Марковица обычно рассматриваются два типа задач оптимизации портфелей:
1.Минимального
риска при заданном уровне доходности;
2. Максимальной доходности при уровне риска не превышающем заданного значения.
2. Максимальной доходности при уровне риска не превышающем заданного значения.
Слайд 411.Портфель Марковица минимального риска.
Найти вектор X* распределения исходного капитала, минимизирующий
риск (вариацию) портфеля
при заданной эффективности портфеля
и условии, что сумма долей активов в портфеле должна составлять единицу
при заданной эффективности портфеля
и условии, что сумма долей активов в портфеле должна составлять единицу
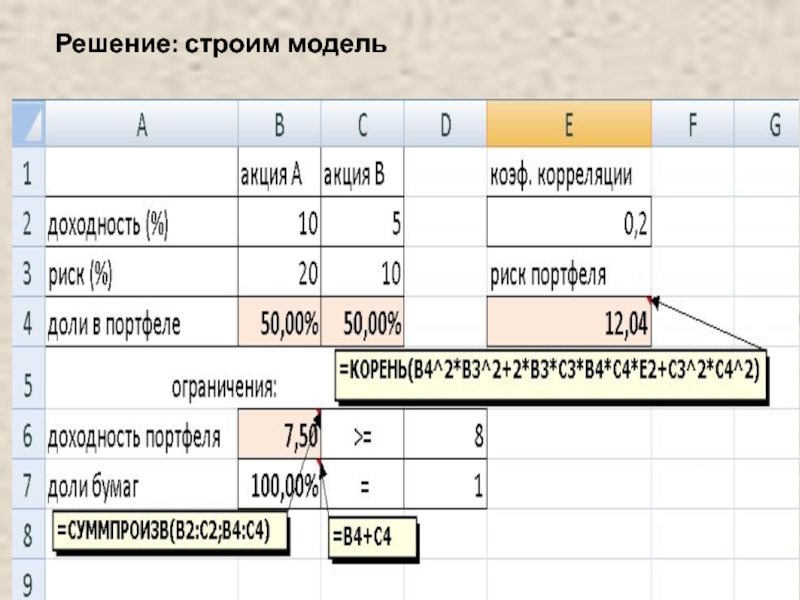
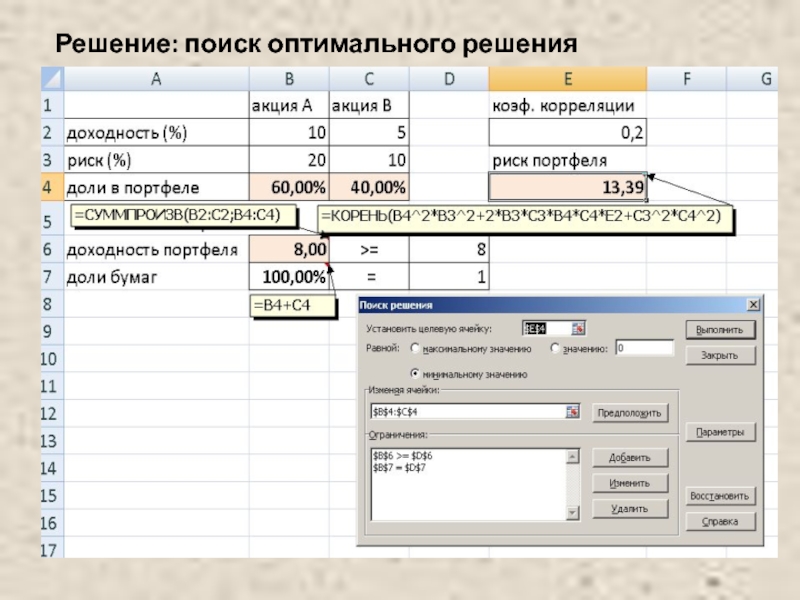
Слайд 42Пример
Сформировать портфель минимального риска из двух видов ценных бумаг -
А с доходностью 10% и риском 20% и В с доходностью 5% и риском 10% при условии, что обеспечивается доходность портфеля не менее 8%. Коэффициент корреляции равен 0.2.
Решение.
Модель Марковица может быть сформулирована следующим образом.
Необходимо найти вектор Х= (X1, X2), минимизирующий риск портфеля σp.
Решение.
Модель Марковица может быть сформулирована следующим образом.
Необходимо найти вектор Х= (X1, X2), минимизирующий риск портфеля σp.
Слайд 452.Портфель Марковица максимальной эффективности.
Найти вектор X*, максимизирующий ожидаемую эффективность портфеля
при уровне риска не превышающем заданного значения-σe
и условии, что сумма долей активов в портфеле должна составлять единицу
Слайд 50 Модель Тобина
Рассмотренный ранее
подход Марковица к инвестициям обобщается.
Во-первых, инвестору разрешается инвестировать не только в рискованные, но и в безрисковые активы. Это означает, что теперь имеется N активов, доступных для инвестиций, включая(N -1) рискованный актив и один безрисковый.
Во-вторых, инвестору разрешается одалживать деньги при обязательных выплатах по определенной процентной ставке по взятым займам.
Кроме того, рассматривается эффект от добавления безрискового актива к набору рискованных активов.
Во-первых, инвестору разрешается инвестировать не только в рискованные, но и в безрисковые активы. Это означает, что теперь имеется N активов, доступных для инвестиций, включая(N -1) рискованный актив и один безрисковый.
Во-вторых, инвестору разрешается одалживать деньги при обязательных выплатах по определенной процентной ставке по взятым займам.
Кроме того, рассматривается эффект от добавления безрискового актива к набору рискованных активов.
Слайд 51Безрисковый актив
Безрисковый актив имеет, по определению, известную доходность, этот тип
актива должен быть некой ценной бумагой, обеспечивающей фиксированный доход и имеющей нулевую вероятность неуплаты. Поскольку все корпоративные ценные бумаги имеют некоторую вероятность неуплаты, то безрисковый актив не может быть выпущен корпорацией.
Безрисковым активом может быть лишь ценная бумага, выпущенная правительством. Однако не каждая ценная бумага, выпущенная правительством, является безрисковой.
Безрисковым активом может быть лишь ценная бумага, выпущенная правительством. Однако не каждая ценная бумага, выпущенная правительством, является безрисковой.
Слайд 52Есть только один тип казначейских бумаг, удовлетворяющих требованию безрисковости: казначейская ценная
бумага со сроком погашения, совпадающим с периодом владения. Например, инвестор при трехмесячном периоде владения обнаружит, что казначейский вексель с трехмесячным сроком погашения предоставляет фиксированный доход. Так как ценная бумага погашается в конце периода владения, то инвестор получает в этот момент количество денег, которое уже известно при принятии инвестиционного решения.
Инвестирование в безрисковый актив часто называют безрисковым кредитованием, поскольку подобное инвестирование состоит в покупке казначейских векселей и поэтому означает предоставление займа правительству.
Инвестирование в безрисковый актив часто называют безрисковым кредитованием, поскольку подобное инвестирование состоит в покупке казначейских векселей и поэтому означает предоставление займа правительству.
Слайд 53Безрисковое заимствование.
Пусть инвестор не ограничен своим начальным капиталом при принятии
решения о том, сколько денег инвестировать в рискованные активы. Однако если инвестор занимает деньги, то он должен платить процент по займу. Если процентная ставка известна и неопределенность с выплатой займа отсутствует, то это часто называется безрисковым заимствованием. Предполагается, что процентная ставка по займу равна ставке, которая может быть заработана инвестированием в безрисковые активы . Это означает, что инвестор имеет возможность не только инвестировать в безрисковый актив под, например, 4%, но также он может получить заем, за который обязан платить процентную ставку, равную 4%.
Слайд 54
Замечание
Прежде считалось, что доля, инвестированная в безрисковый актив, является положительным числом от нуля до единицы. Поскольку теперь имеется возможность получать заем по той же процентной ставке, то эти ограничения снимаются. Если инвестор займет деньги, то он будет иметь большую сумму для инвестиций в ценные бумаги компаний, но их доля в портфеле учитывается , как отрицательная величина.
Слайд 55Модель Тобина-Шарпа-Литнера
(D. Tobin –лауреат Нобелевской премии)
В
этой модели портфель состоит из безрискового актива , доходность которого не зависит от состояния рынка и имеет постоянное значение - mf – эффективность безрисковых бумаг, а x f – доля капитала, в него вложенного, тогда в рисковую часть портфеля будет вложена (1- xf) часть всего капитала. Пусть mr – эффективность и σ2 r –(дисперсия) рисковой части портфеля.
Слайд 56Модель Тобина-Шарпа-Литнера для 2-х бумаг.
Считается, что безрисковые бумаги не коррелируют
с остальными.
Эффективность всего портфеля равна
Вариация портфеля равна:
Риск портфеля:
Эффективность всего портфеля равна
Вариация портфеля равна:
Риск портфеля:
Слайд 593.Модель Тобина c n рисковыми бумагами.
Модель Тобина – комбинированный портфель включающий
, как рисковые , так и безрисковую ценную бумагу с гарантированной доходностью – mf и долей xf.
Найти вектор X* распределения исходного капитала, минимизирующий риск (вариацию) портфеля
при заданной эффективности портфеля и условии, что сумма долей активов в портфеле должна составлять единицу
x.=>0
Найти вектор X* распределения исходного капитала, минимизирующий риск (вариацию) портфеля
при заданной эффективности портфеля и условии, что сумма долей активов в портфеле должна составлять единицу
x.=>0
Слайд 60Заимствование и инвестирование в рискованные
ценные бумаги
1) Любой портфель, состоящий из комбинации безрискового и рискованного активов, будет иметь ожидаемую доходность и стандартное отклонение, которые лежат на одной прямой, соединяющей точки, соответ-ствующие этим активам.
2) Все портфели, содержащие безрисковое заимствование, лежат на той же самой прямой линии, что и портфели, включающие безрисковое кредитование. При этом чем больше величина взятого займа, тем дальше на прямой располагается портфель.
Слайд 61Можно показать, что любая комбинация заимствования и инвестирования в акции какой-либо
компании лежит на этой прямой и ее точное расположение зависит от величины займа. Это свойство можно обобщить на основе комбинации безрискового заимствования и инвестиций в любые конкретные рискованные активы. Это означает, что получение займа по безрисковой ставке и инвестирование всех занятых и собственных денег в рискованный актив приведет к формированию портфеля, который имеет такую же ожидаемую доходность и стандартное отклонение, что и портфель находящийся на прямой линии, проходящей через точку безрисковой ставки и точку рискованного актива.
Слайд 63
Замечания
Доходность безрискового актива является заранее известной. Стандартное отклонение для безрискового актива равно нулю, так же как и его ковариация с другими активами.
При расширении множества достижимости Марковица за счет возможности предоставления безрисковых займов предполагается, что инвесторы распределяют свои средства между безрисковым активом и портфелем рискованных активов.
С учетом безрискового кредитования эффективное множество на графике приобретает вид прямого отрезка, исходящего из точки, соответствующей безрисковой ставке, к точке касания с эффективным множеством Марковица, а также к части эффективного множества Марковица, лежащей выше и правее точки касания.
Безрисковые заимствования являются для инвестора «финансовым рычагом». Он может использовать все свои деньги, а также деньги, занятые по безрисковой ставке, для покупки портфеля рискованных активов.
Слайд 64Если возможно безрисковое заимствование и кредитование, то эффективное множество становится лучем,
исходящим из точки соответствующей безрисковой ставки и проходящим через точку, касательную к кривой эффективного множества Марковица.
При возможности безрискового заимствования и кредитования эффективное множество состоит из одного рискованного портфеля и различных комбинаций безрискового кредитования или заимствования.
Графически оптимальный портфель инвестора определяется при помощи изображения его кривых безразличия одновременно с эффективным множеством.
Инвестор, более склонный к избеганию риска, предпочтет меньший уровень заимствований (или больший уровень кредитования), чем инвестор, менее склонный избегать риск.
При возможности безрискового заимствования и кредитования эффективное множество состоит из одного рискованного портфеля и различных комбинаций безрискового кредитования или заимствования.
Графически оптимальный портфель инвестора определяется при помощи изображения его кривых безразличия одновременно с эффективным множеством.
Инвестор, более склонный к избеганию риска, предпочтет меньший уровень заимствований (или больший уровень кредитования), чем инвестор, менее склонный избегать риск.
Слайд 65
Модель Блэка
В модели Блэка допустимыми являются любые портфели, т.е. вектор Х удовлетворяет лишь основному ограничению:
Наличие коротких позиций (отсутствие условия неотрицательности) позволяет реализовать любую, сколь угодно большую доходность, естественно за счет большого риска.
Слайд 66
Выводы
Современная портфельная теория основывается на допущении, что инвесторы имеют возможность распределять богатство среди множества доступных направлений инвестирования, - то есть формировать инвестиционный портфель. Причем критериями оценки эффективности инвестиционных решений являются только два параметра - ожидаемая доходность и стандартное отклонение доходности.
Эффект диверсификации состоит в возможности снижения риска инвестирования (без ущерба для доходности) путем распределения инвестиций среди доступных направлений. Чем больше степень диверсификации и чем меньше корреляция между доходностью выбранных финансовых активов - тем большими являются возможности по снижению риска.
Слайд 67Предоставляемые рынком возможности по выбору желаемой комбинации ожидаемой доходности и риска
инвестиций ограничены. Эффективным портфелем называется портфель с максимальной для данной величины риска ожидаемой доходностью, либо, что то же самое - с минимальным для данной величины доходности риском. Совокупность всех возможных эффективных портфелей образует границу эффективности. Рациональные инвесторы всегда стремятся к формированию эффективного портфеля. Какой именно эффективный портфель выберет инвестор - зависит от его индивидуальных отношений предпочтения между риском и ожидаемым доходом. Если на рынке существует безрисковая ставка доходности, задача инвестора сводится к выбору комбинации рискованных и безрисковых инвестиций.
Слайд 68Модель Марковица представляет собой задачу выбора эффективного портфеля - то есть
формирования портфеля, обеспечивающего минимальный риск при заданном уровне ожидаемой доходности. В общем случае, модель Марковица представляет собой задачу квадратичного программирования и может быть решена стандартными методами. Наиболее сложная проблема, связанная с практическим использованием модели Марковица - подготовка исходной информации об ожидаемой доходности, стандартном отклонении и коэффициентах ковариации финансовых активов.
