*
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 1. Сущность финансового менеджмента. Лекция 2. Методологическая основа управления финансами компании презентация
Содержание
- 1. Тема 1. Сущность финансового менеджмента. Лекция 2. Методологическая основа управления финансами компании
- 2. Теория ценообразования опционов
- 3. Структура капитала (capital structure, Csr)
- 5. Методологическая основа финансового менеджмента Теория идеальных рынков
- 6. Модель идеального рынка Полное отсутствие трансакционных затрат
- 7. Альтернативная стоимость – стоимость упущенных возможностей Альтернативные
- 8. Дисконтированная стоимость (present value)
- 9. Дисконтирование Пример: Для того, чтобы определить сегодняшний
- 10. Расчет аннуитета (annuity)
- 11. Капитализированная стоимость (capitalized value, CV)
- 12. Проект
- 13. Проект С
- 14. Начисление простого процента (simple interest)
- 15. Начисление сложного процента (compounding interest) if=(1+i)n –
- 16. Начисление сложного процента (продолжение) При многократном начислении
- 17. Определение будущей стоимости (future value) FVn =
Слайд 1Тема 1. Сущность финансового менеджмента (продолжение)
Лекция 2.
Методологическая основа управления финансами
Слайд 2
Теория ценообразования опционов
Опцион – право выбора
Разновидность производной ценной бумаги (право купить или продать пакет ценных бумаг в будущем по заранее оговоренной цене)
Реальные опционы характеризуются управленческой гибкостью при реализации инвестиционных проектов (на отказ, на задержку, на переключение, на увеличение масштаба, на уменьшение масштаба, на усовершенствование)
Слайд 3Структура капитала
(capital structure, Csr)
Cst = E/L
E (equity) -
L (liabilities) - обязательства
Пример:
Так, если компания осуществляет свое финансирование на 40 % за счет заемных средств (обязательств), а на 60 % за счет собственного капитала, то структура ее капитала представляет собой соотношение собственных и заемных средств:
60 : 40 = 1,5
Это означает, что компания на 3/5 профинансирована за счет собственных средств, а на 2/5 – в долг.
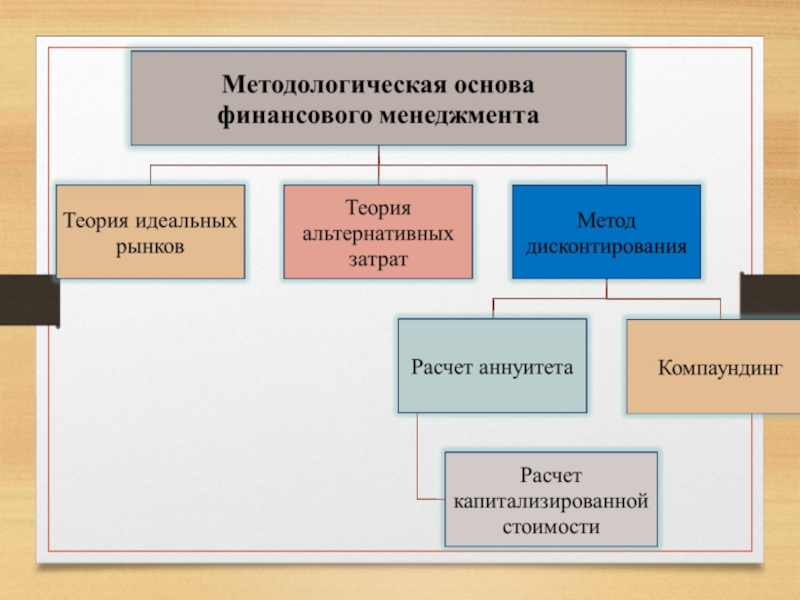
Слайд 5Методологическая основа финансового менеджмента
Теория идеальных рынков (perfect capital market)
Теория альтернативной стоимости
Метод дисконтирования (discounting)
Слайд 6Модель идеального рынка
Полное отсутствие трансакционных затрат
Отсутствие налогов
Большое количество участников сделок
Равный доступ
Равнодоступность информации
Одинаковые ожидания
Отсутствие затрат, связанных с финансовыми затруднениями
Слайд 7Альтернативная стоимость – стоимость упущенных возможностей
Альтернативные затраты – выгода, потерянная вследствие
Слайд 8Дисконтированная стоимость
(present value)
PV (present value) - текущая стоимость будущих денег
FVn (future
n - количество периодов
i (interest rate) - ставка дисконтирования
Слайд 9Дисконтирование
Пример:
Для того, чтобы определить сегодняшний эквивалент некой суммы денег, например 20
20/(1 + 0,18) 2 = 14,3 (тыс. руб.)
Это означает, что, имея сегодня 14,3 тысячи рублей, можно положить их в банк под 18 % годовых и получить через 2 года 20 тысяч рублей.
Слайд 10Расчет аннуитета (annuity)
PVa = ∑An/(1 + i) n
PVa
An (annuity) - аннуитет
n - количество периодов
i ( interest rate) - ставка дисконтирования
Пример:
Вам предложили положить в банк на три года некую сумму под 4 % годовых, которая будет приносить ежегодный доход в 1 тысячу долларов. Для того, чтобы определить сегодняшнюю стоимость будущих доходов, необходимо привести их к текущему моменту времени:
1000/(1+0,04) + 1000/(1+0,04)2 +1000/(1+0,04)3 = 962 + 925 + 889 = 2776 (долл.)
Слайд 11Капитализированная стоимость (capitalized value, CV)
CV =Ra/i, при n
Ra (англ. annual revenue) - сумма ежегодного дохода
i (англ. interest rate) - ставка дисконтирования
n - количество периодов
Пример:
Для того, чтобы определить стоимость актива, например, участка земли, который при сдаче в аренду приносит 4 тысячи долларов ежегодно в виде арендной платы, необходимо разделить эту сумму на ставку дисконта, например, 5 %, тогда капитализированная стоимость данного участка равна:
4/0,05= 80 (тыс. долл.)
Это означает, что Вы можете продать данный участок за 80 тысяч долларов, положить эту сумму в банк под 5 % годовых и получать ежегодно 4 тысячи долларов.
В данном случае этот доход выступает в качестве аннуитета.
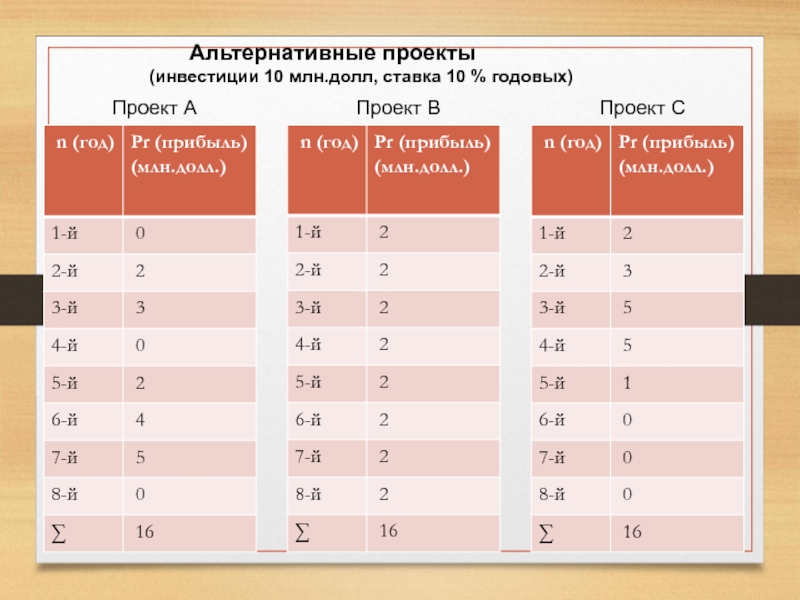
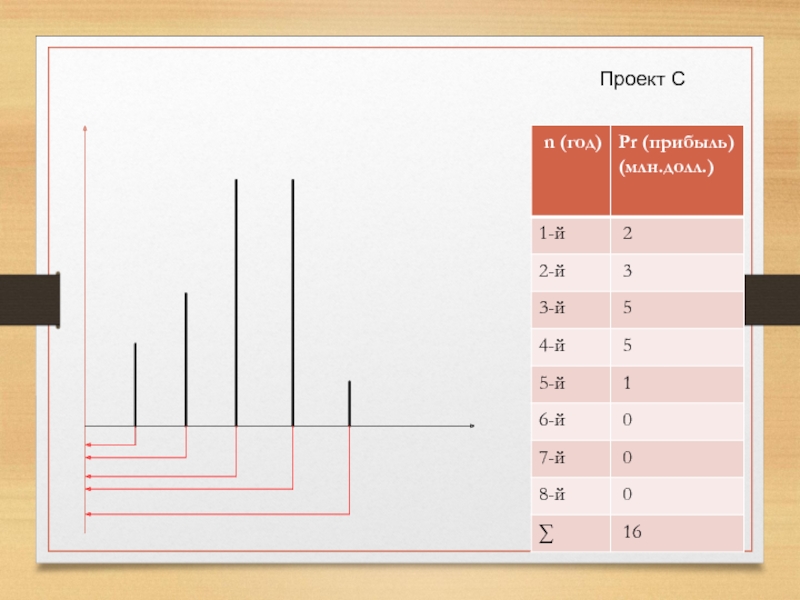
Слайд 12 Проект С
Проект А
Альтернативные проекты
(инвестиции 10 млн.долл, ставка 10 % годовых)
Слайд 14Начисление простого процента
(simple interest)
∑ Int s = Cr * i
∑ Int s (simple interests) - сумма, которую нужно выплатить в качестве процентов по кредиту, при простом проценте
i (interest rate) - процентная ставка,
n - период времени (число периодов).
Cr (credit) - основная сумма кредита
Пример:
Процентная ставка равная 15 % ежегодно, означает, что за каждые взятые в долг на один год 100 долларов заемщик должен заплатить 15 долларов. Если Вы хотите взять кредит в размере 2 тыс.долл. на 3 года под простой процент 15 % годовых, то сумма, которую Вы должны выплатить по обслуживанию этого долга, составит:
2000 * 0,15 * 3 = 900 (долл.)
Слайд 15Начисление сложного процента
(compounding interest)
if=(1+i)n – 1
Int c= Cr (1+i)n – Cr
Пример:
Так, если бы в предыдущем примере начислялся не простой, а сложный процент, то его сумма составила бы:
2000 (1 + 0,15) (1 + 0,15) (1 + 0,15) – 2000 = 1041,75 (долл.)
Слайд 16Начисление сложного процента
(продолжение)
При многократном начислении в течение года формула сложного процента
if = (1 +i/t)m ΣIntc = Cr(1 +i/t)m – Cr
m= n * t - число периодов
t - число периодов начисления процента за год
Пример:
Если сумма в 500 долл. была взята на два года под 12 % при поквартальном начислении сложного процента, то количество периодов составит 4х2=8,а выплата процентов 12 :4 =3%. Отсюда сумма процентов равна 500(1 +0,03)8 – 500= 133,38 долл. При начислении простого процента эта сумма составила бы 120 долл.
Слайд 17Определение будущей стоимости (future value)
FVn = PV (1 + i)n
FVn (англ.
PV (англ. present value) - настоящая (текущая) стоимость денег
Пример:
Будущая стоимость 1 тысячи долларов через три года при ставке процента равной 5 % годовых равна:
1000 (1 + 0,05)3 = 1157,6 (долл.)