- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Простые проценты. Наращение и дисконтирование. Лекция 1 презентация
Содержание
- 1. Простые проценты. Наращение и дисконтирование. Лекция 1
- 2. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Обозначения I —
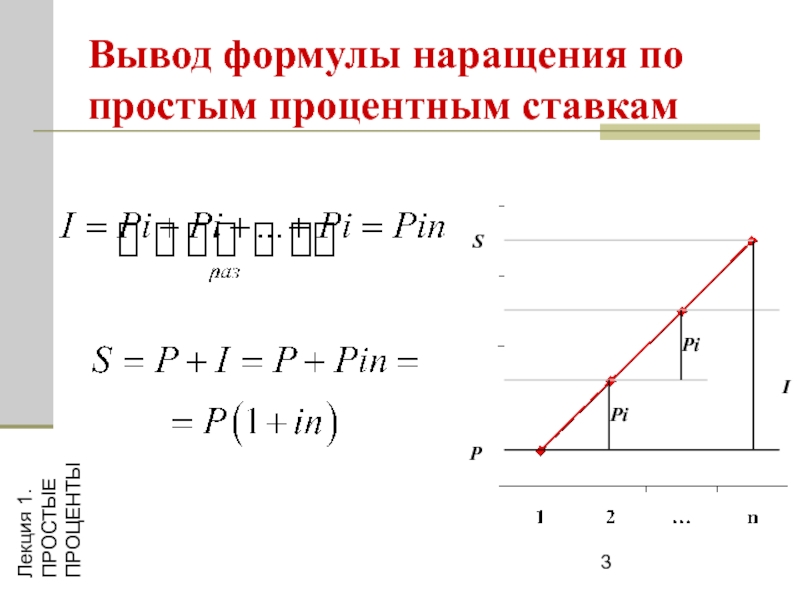
- 3. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Вывод формулы наращения
- 4. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Практика расчета процентов
- 5. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Виды временной базы
- 6. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Переменные ставки
- 7. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Переменные ставки В
- 8. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Начисление процентов при изменении сумм депозита во времени
- 9. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Начисление процентов при
- 10. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Начисление процентов при
- 11. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Реинвестирование по простым
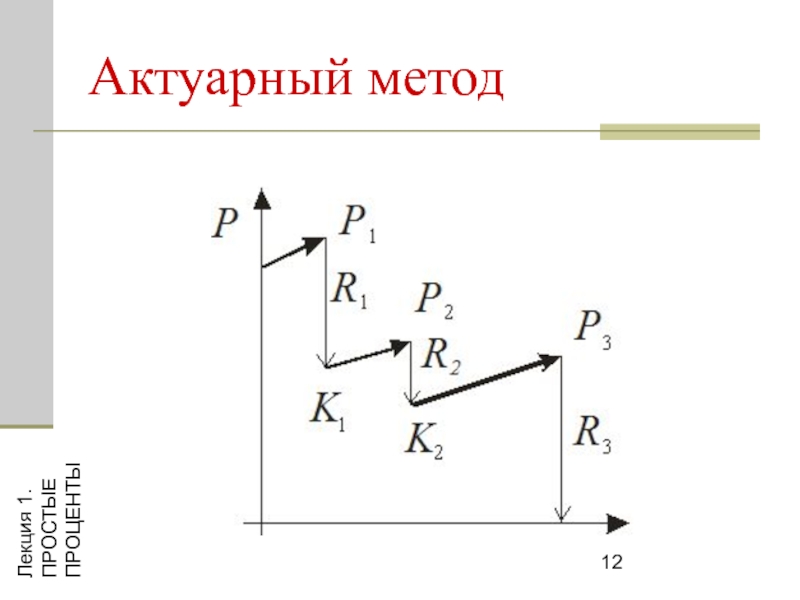
- 12. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Актуарный метод
- 13. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Формула для
- 14. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Правило торговца
- 15. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Правило торговца
- 16. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Наращение процентов в
- 17. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Математическое дисконтирование
- 18. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Банковский учет (учет
- 19. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Наращение по учетной
- 20. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Срок ссуды Из
- 21. Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ Величина процентной ставки
Слайд 2Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Обозначения
I — проценты за весь срок ссуды;
Р —
первоначальная сумма долга;
S — наращенная сумма, т. е. сумма в конце срока;
i — ставка наращения процентов;
n — срок ссуды.
S — наращенная сумма, т. е. сумма в конце срока;
i — ставка наращения процентов;
n — срок ссуды.
Слайд 4Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Практика расчета процентов для краткосрочных ссуд
Выразим срок
ссуды n в виде дроби
,
где t — число дней ссуды,
К — число дней в году, или временная база начисления процентов.
,
где t — число дней ссуды,
К — число дней в году, или временная база начисления процентов.
Слайд 5Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Виды временной базы
Германская система: К = 360 дней
(12
месяцев по 30 дней в каждом месяце);
Французская система: К = 360 дней
(12 месяцев с номинальным количеством дней в каждом месяце);
Английская система: К = 365 (366) дней
(12 месяцев с номинальным количеством дней в каждом месяце).
Если К = 360, то получают обыкновенные или коммерческие проценты.
Если К = 365 (366) рассчитывают точные проценты.
Французская система: К = 360 дней
(12 месяцев с номинальным количеством дней в каждом месяце);
Английская система: К = 365 (366) дней
(12 месяцев с номинальным количеством дней в каждом месяце).
Если К = 360, то получают обыкновенные или коммерческие проценты.
Если К = 365 (366) рассчитывают точные проценты.
Слайд 7Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
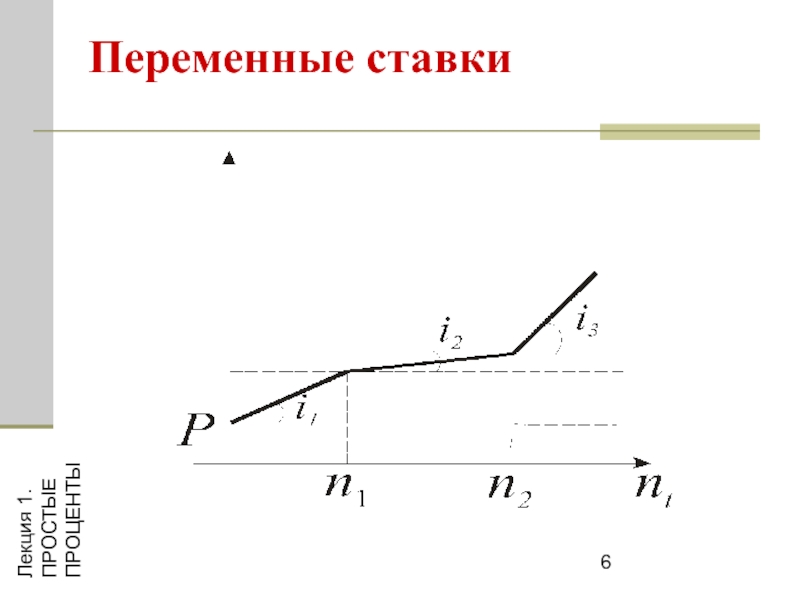
Переменные ставки
В случае если процентные ставки простые, то
наращенная на конец срока сумма определяется следующим образом:
где it - ставка простых процентов в периоде t,
nt - продолжительность периода с постоянной ставкой
где it - ставка простых процентов в периоде t,
nt - продолжительность периода с постоянной ставкой
Слайд 9Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
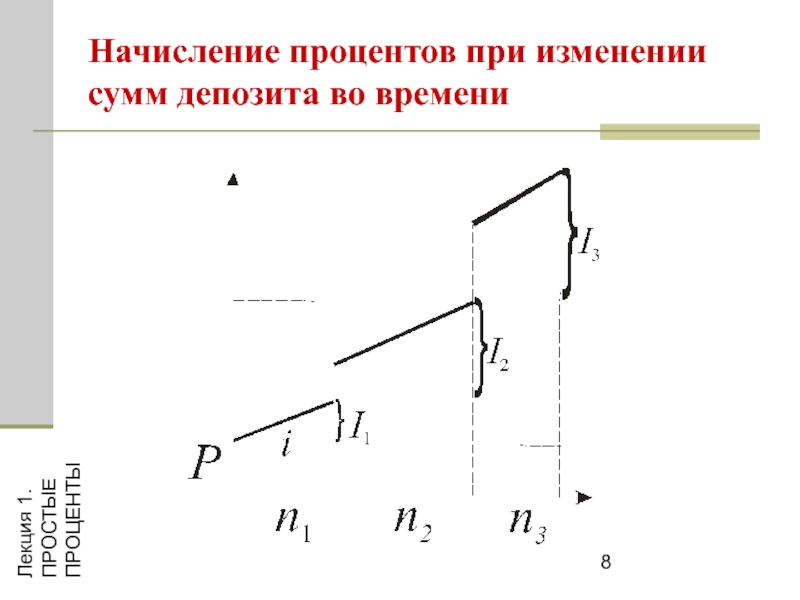
Начисление процентов при изменении сумм депозита во времени
Пусть
Rj - остаток средств на счете в момент j после очередного поступления или списания средств,
nj - срок хранения денег (в годах) до нового изменения остатка средств на счете.
Тогда суммарные проценты за весь срок финансовой операции будут равны
nj - срок хранения денег (в годах) до нового изменения остатка средств на счете.
Тогда суммарные проценты за весь срок финансовой операции будут равны
Слайд 10Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Начисление процентов при изменении сумм депозита во времени
Если
период nt, через который происходит изменение остатка на счете, не совпадает с периодом начисления процентов, следует произвести пересчет процентной ставки, т.е.
K означает число дней в году, а tj — срок в днях между последовательными изменениями остатков на счете.
K означает число дней в году, а tj — срок в днях между последовательными изменениями остатков на счете.
Слайд 11Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Реинвестирование по простым ставкам
Наращенная сумма для всего срока
при реинвестировании составит
it — размер ставок, по которым производится реинвестирование.
Если промежуточные сроки начисления и ставки не изменяются во времени, то имеем
т — количество повторений реинвестирования.
it — размер ставок, по которым производится реинвестирование.
Если промежуточные сроки начисления и ставки не изменяются во времени, то имеем
т — количество повторений реинвестирования.
Слайд 13Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Формула для определения остатка задолженности (Кj)
Задолженность на конец
срока должна быть полностью погашена, т.е.
Слайд 15Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
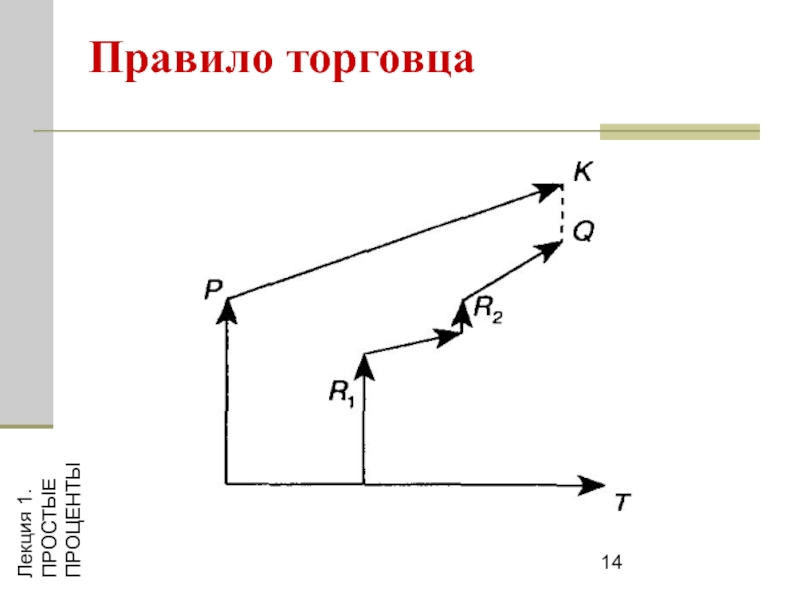
Правило торговца
где
Q — остаток долга на конец срока
или года,
S — наращенная сумма долга,
K — наращенная сумма платежей,
Rj — сумма частичного платежа,
n — общий срок ссуды,
tj — интервал времени от момента платежа до конца срока ссуды или года.
S — наращенная сумма долга,
K — наращенная сумма платежей,
Rj — сумма частичного платежа,
n — общий срок ссуды,
tj — интервал времени от момента платежа до конца срока ссуды или года.
Слайд 16Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Наращение процентов в потребительском кредите
Наращенная сумма долга
Величина разового
погасительного платежа составляет
n – срок кредита в годах m – число платежей в году
n – срок кредита в годах m – число платежей в году
Слайд 17Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
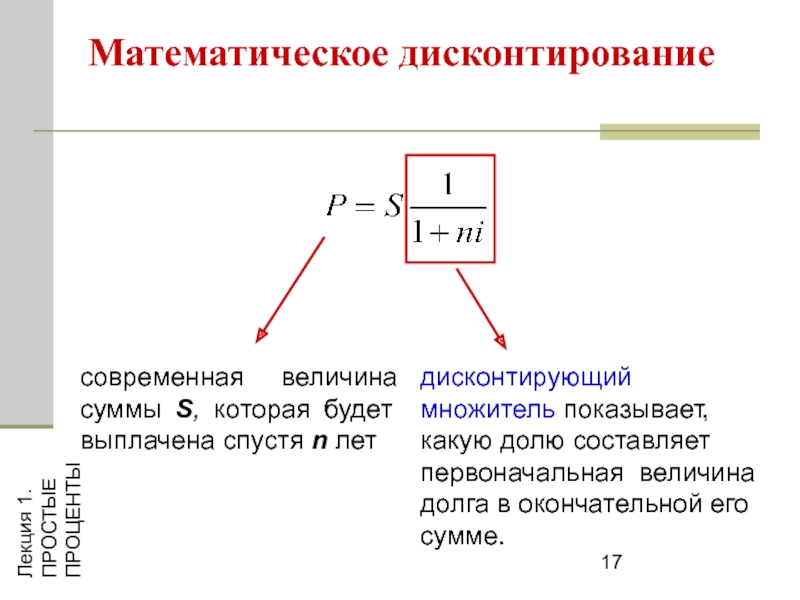
Математическое дисконтирование
современная величина суммы S, которая будет
выплачена спустя n лет
дисконтирующий множитель показывает, какую долю составляет первоначальная величина долга в окончательной его сумме.
Слайд 18Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Банковский учет (учет векселей)
Размер дисконта, или суммы учета
равен Snd; если d — годовая учетная ставка, то n измеряется в годах.
Р = S – Snd = S(1 - nd),
где п — срок от момента учета до даты погашения векселя.
Дисконтный множитель равен (1 - nd).
При этом используется французская система подсчета срока начисления процентов.
Р = S – Snd = S(1 - nd),
где п — срок от момента учета до даты погашения векселя.
Дисконтный множитель равен (1 - nd).
При этом используется французская система подсчета срока начисления процентов.
Слайд 19Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Наращение по учетной ставке
Простая учетная ставка иногда
применяется при расчете наращенной суммы: в этом возникает необходимость при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга.
Наращенная сумма в этом случае
Наращенная сумма в этом случае
Слайд 20Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Срок ссуды
Из формул наращения и дисконтирования выразим п
срок в годах.
Слайд 21Лекция 1. ПРОСТЫЕ ПРОЦЕНТЫ
Величина процентной ставки
Из формул наращения и дисконтирования выразим
i или d, и получим выражения для сроков, измеренных в годах и днях:
n = t / K, где K – временная база
n = t / K, где K – временная база