- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы оптимальных решений. Решение прикладных задач презентация
Содержание
- 1. Методы оптимальных решений. Решение прикладных задач
- 2. Решение прикладных задач Дано словесное описание
- 3. Задача №1. Завод выпускает два вида
- 4. Прибыль данного предприятия от реализации производимой продукции
- 5. и прибыль предприятия, задаваемая функцией ,
- 6. Задача №2 Предприятие располагает ресурсами сырья и
- 7. Прибыль данного предприятия от реализации производимой продукции
- 8. и прибыль предприятия, задаваемая функцией ,
- 9. Задача №3 Предприятие производит продукцию двух видов,
- 10. Задача №4 Предприятие имеет ресурсы А и
- 11. Прибыль данного предприятия от реализации производимой продукции
- 12. Задача №5 Компания, занимающаяся добычей руды, имеет
- 13. Решение: Итак, определим модель транспортной задачи,
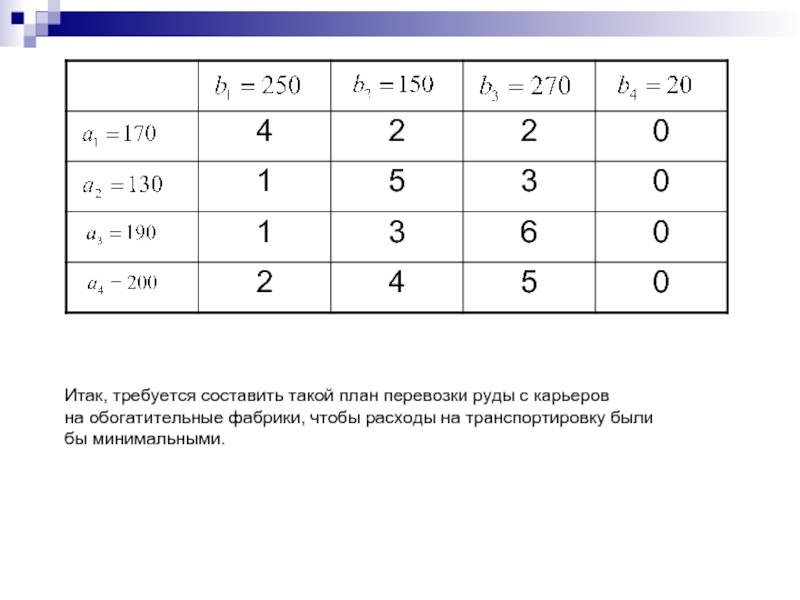
- 14. Итак, требуется составить такой план перевозки руды
- 15. Задача №6 На предприятии имеется три группы
- 16. Сравнивая суммарное время работы каждой группы станков
Слайд 2Решение прикладных задач
Дано словесное описание задачи. Привести ее табличное и
Слайд 3Задача №1. Завод выпускает два вида строительных материалов: жидкое стекло и
Решение:
Пусть завод выпускает т. стекла, т. пенопласта, тогда по условию задачи мы имеем систему неравенств - ограничений:
Слайд 4Прибыль данного предприятия от реализации производимой продукции составит
Слайд 6Задача №2 Предприятие располагает ресурсами сырья и рабочей силы, необходимыми для производства
Решение:
Пусть предприятие выпускает единиц продукции I – го вида, единиц продукции II – го вида. Тогда по условию задачи мы имеем систему неравенств - ограничений:
Слайд 7Прибыль данного предприятия от реализации производимой продукции составит
Итак, мы получили следующую задачу линейного программирования. Руководству предприятия необходимо определить такие и объемы производимой продукции, чтобы выполнялись условия-ограничения:
Слайд 9Задача №3 Предприятие производит продукцию двух видов, используя для этого ресурсы трех
Технологическая матрица ,
вектор
Пусть предприятие выпускает
единиц продукции I – го вида,
единиц продукции II – го вида,
- система ограничений.
Решение:
Слайд 10Задача №4 Предприятие имеет ресурсы А и Б в количестве 240 и
Решение:
Пусть предприятие выпускает единиц изделий I – го вида, единиц изделий II – го вида. Тогда по условию задачи мы имеем систему неравенств - ограничений:
Слайд 11Прибыль данного предприятия от реализации производимой продукции составит
Итак, мы получили следующую задачу линейного программирования. Руководству предприятия необходимо определить такие и объемы производимых изделий, чтобы выполнялись условия-ограничения:
и прибыль предприятия, задаваемая функцией
была бы максимальной.
Слайд 12Задача №5 Компания, занимающаяся добычей руды, имеет четыре карьера. Производительность карьеров соответственно
Слайд 13Решение:
Итак, определим модель транспортной задачи, для этого проверим условие.
Сравнивая суммарную производительность
и суммарные мощности обогатительных фабрик потребность
в руде, установим, является ли модель транспортной задачи, заданная этой таблицей,
открытой или закрытой.
(тыс. т.).
(тыс. т.).
с нулевыми затратами на перевозку. В результате чего получаем следующую модель
транспортной задачи.
Слайд 14Итак, требуется составить такой план перевозки руды с карьеров на обогатительные
Слайд 15Задача №6
На предприятии имеется три группы станков, каждая из которых может
Решение:
Слайд 16Сравнивая суммарное время работы каждой группы станков
Итак, определим модель транспортной задачи, для этого проверим условие
(часов).
(часов).
Так как
Итак, необходимо составить такой план работы станков, при котором
производительность предприятия будет максимальной.
, то модель транспортной задачи является закрытой.