- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Comparing alternatives презентация
Содержание
- 1. Comparing alternatives
- 2. Comparing Alternatives
- 3. The Objective To learn how to
- 4. Three groups of investment alternatives 1. Mutually
- 5. The fundamental purpose of capital investment is
- 6. Investment alternatives and cost alternatives An Investment
- 7. The study period must be appropriate for
- 8. Case 1: Study period = Useful life
- 9. Equivalent Worth (EW) Methods: PW, AW, FW
- 10. Example: Investment Alternatives Study period = Useful
- 11. Solution PW(12%) = -I + A(P/A,
- 12. Example: Cost Alternatives Study period = Useful
- 13. Solution AW = I(A/P, 12%, 7)
- 14. IRR Method: Why not select the investment
- 15. IRR Method: Another Example Given three MEAs
- 16. Solution steps Step 2: compare DN with
- 17. Solution steps Step 4: compare alternative 2
- 18. Solution steps Step 4: next comparison: alternative
- 19. Case 2: Study period ≠ Useful life
- 20. Study period ≠ Useful life Up until
- 21. Example: 5-24 Cost alternative: Study period>Useful
- 22. Example: 5-24 - Solution Consider the AW
- 23. Example: 5-24 – PW Solution based on
- 24. What if the study period is not
- 25. Study period > Useful life Use the
- 26. Case 2: Study period < useful life
- 27. Example: Cotermination Useful life of A =
- 28. Example: Solution AW(A) (10%) = -50,000(A/P,10, 20)
- 29. Example: Solution Market Value of Boiler B
Слайд 1American University of Armenia
IE 340 – Engineering Economics
Spring Semester, 2016
Ch5- Comparing
Слайд 3The Objective
To learn how to properly apply the profitability measures
The cash-flow analysis methods (previously described) used in this process:
Present Worth ( PW )
Annual Worth ( AW )
Future Worth ( FW )
Internal Rate of Return ( IRR )
External Rate of Return ( ERR )
Слайд 4Three groups of investment alternatives
1. Mutually exclusive
At
Example: suppose you are shopping for a car. You consider several cars, but will only buy one from a mutually exclusive set of choices
2. Independent
The choice of a project is independent of the choice of any other project in the group, so that all or none of the projects may be selected or some number in between
3. Contingent
The choice of the project is conditional on the choice of one or more other projects
Слайд 5The fundamental purpose of capital investment is to obtain at least
Basic Rule:
Spend the least amount of capital possible unless the extra capital can be justified by the extra savings or benefits
In other words, any increment of capital spent (above the minimum) must be able to pay its own way
Слайд 6Investment alternatives and cost alternatives
An Investment Alternative has an initial investment
"Do nothing" (DN) is usually an implicit investment alternative
If ∑positive cash flows > ∑ negative cash flows, then IRR exists
If PW(MARR) ≥0, investment is profitable
if PW(MARR)<0, do nothing (DN) is better
Cost Alternatives have all negative cash flows except for the salvage value (if applicable)
These alternatives represent “must do” situations, and DN is not an option
IRR not defined for cost alternatives. Can you explain why?
Слайд 7The study period must be appropriate for the decision being made
Study
Useful Life: The period during which an asset is kept in productive operation
We will discuss two cases:
Case 1: Study period = Useful life
Case 2: Study period ≠ Useful life
Fundamental Principle: Compare MEAs over the same period of time
Слайд 9Equivalent Worth (EW) Methods: PW, AW, FW
Procedure for Selecting the Best
Compute the equivalent worth of each alternative, using the MARR as the interest rate
For Investment Alternatives: Select the alternative having the greatest equivalent worth
Note: If all equivalent worths are < 0 for investment alternatives, then "do nothing" is the best alternative
For Cost Alternatives: Select the alternative having the smallest equivalent cost (the one that is least negative)
All three equivalent worth methods (PW, AW, FW) will identify the same "best" alternative
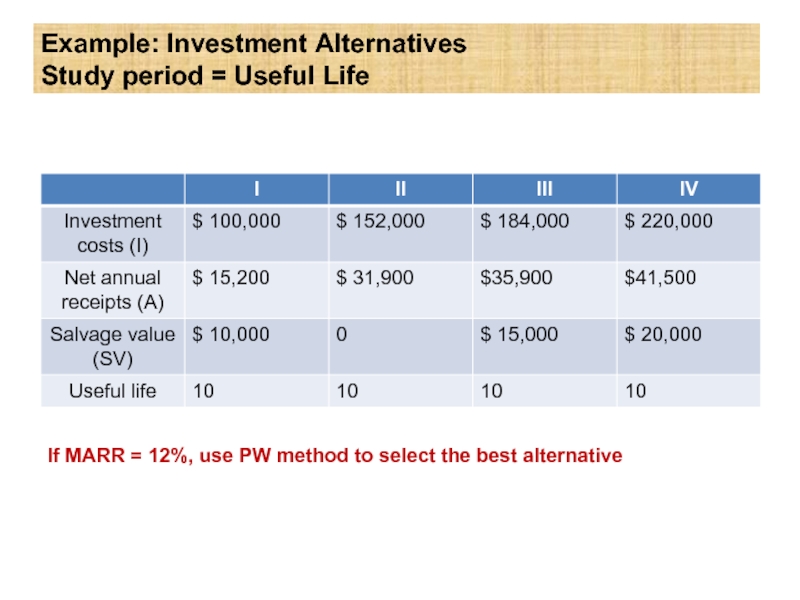
Слайд 10Example: Investment Alternatives
Study period = Useful Life
If MARR = 12%, use
Слайд 11Solution
PW(12%) = -I + A(P/A, 12%, 10) + SV(P/F, 12%, 10)
PW(Do
PWI (12%) = -$10,897
PWII (12%) = +$28.241
PWIII (12%) = +$23,672
PWIV (12%) = +$20,923
Select Alternative ___ to maximize PW.
5.6502
0.3220
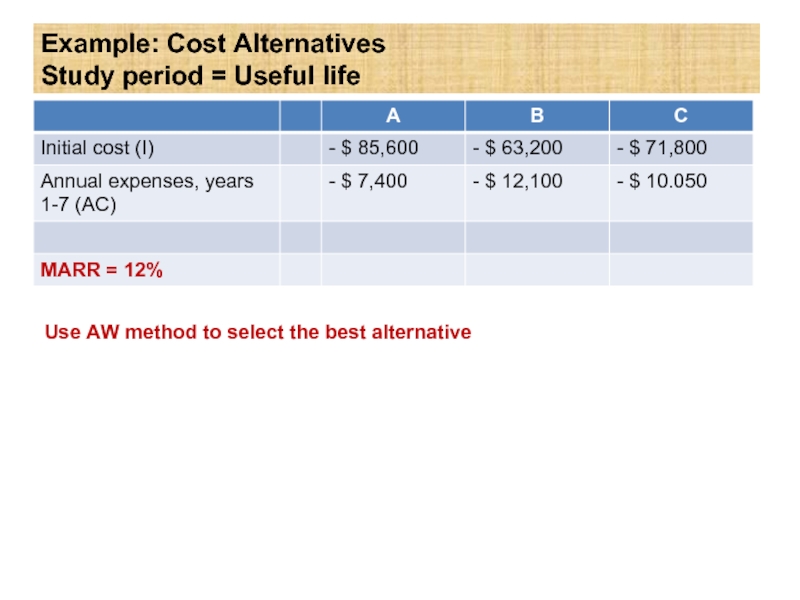
Слайд 12Example: Cost Alternatives
Study period = Useful life
Use AW method to select
Слайд 13Solution
AW = I(A/P, 12%, 7) + AC
AW A = -$85,600(A|P, 12%,
AW B = = -$25,947
AW C = = -$25,781
Assuming one must be chosen (i.e., DN is not an option), select alternative C to minimize annual equivalent costs
0.2191
Слайд 14IRR Method: Why not select the investment opportunity that maximizes IRR?
If
If MARR = 20%, PW(A) = $733 and PW(B )= $2,500
Never simply maximize the IRR!
Never simply select the MEA that maximizes the IRR! Do not maximize the rate of return. Look at the increment
Never compare the IRR to anything except the MARR!
IRR(A→B): PW(B-A) = 0 = -9,900 + 14,000(P/F, i'%, 1)
9,900/14,000 = (P/F, i'%, 1)
i' = 41.4% > MARR . Select B
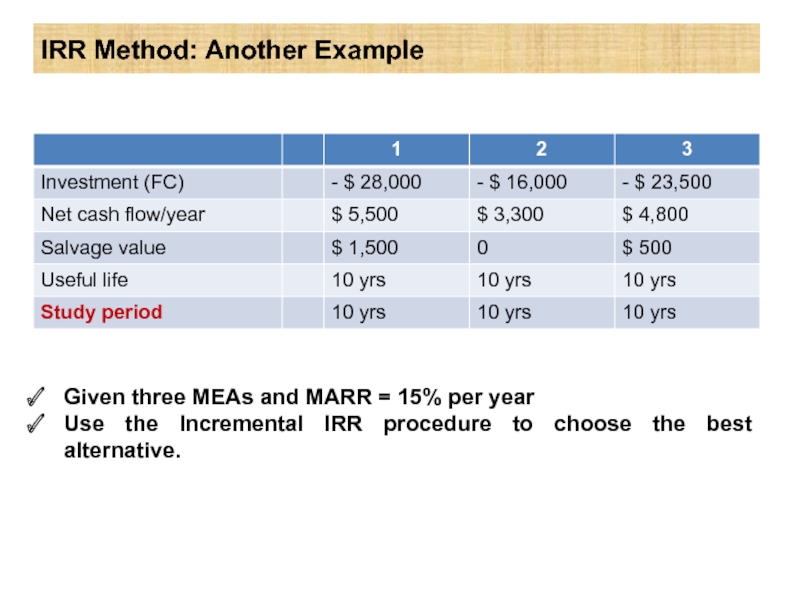
Слайд 15IRR Method: Another Example
Given three MEAs and MARR = 15% per
Use the Incremental IRR procedure to choose the best alternative.
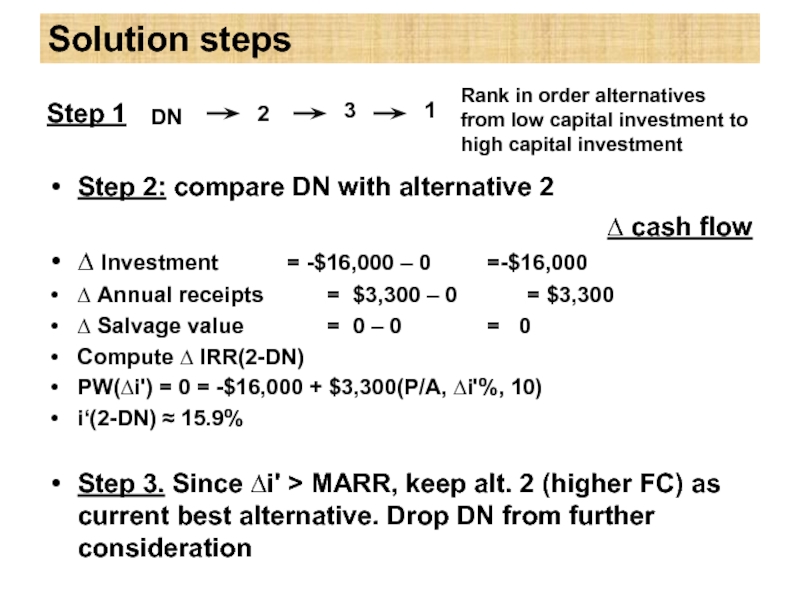
Слайд 16Solution steps
Step 2: compare DN with alternative 2
∆ Investment = -$16,000
∆ Annual receipts = $3,300 – 0 = $3,300
∆ Salvage value = 0 – 0 = 0
Compute ∆ IRR(2-DN)
PW(∆i') = 0 = -$16,000 + $3,300(P/A, ∆i'%, 10)
i‘(2-DN) ≈ 15.9%
Step 3. Since ∆i' > MARR, keep alt. 2 (higher FC) as current best alternative. Drop DN from further consideration
Rank in order alternatives from low capital investment to high capital investment
∆ cash flow
Слайд 17Solution steps
Step 4: compare alternative 2 with alternative 3
∆ Investment =
∆ Annual receipts = $ 4,800 - 3,300 = $1,500
∆ Salvage value = $500 – 0 = $500
Compute ∆ IRR(3-2)
PW(∆ i') = 0 = -$7,500 + $1,500(P/A, ∆i'%, 10) + $500(P/F, ∆i'%, 10)
i‘(3-2) ≈ 15.5%
Since ∆i' > MARR, keep alt. 3 (higher FC) as current best alternative
Drop alt. 2 from further consideration
∆ cash flow
Слайд 18Solution steps
Step 4: next comparison: alternative 3 with alternative 1
∆ Investment
∆ Annual receipts = $ 5,500 - 4,800 = $700
∆ Salvage value = $1,500 -500 = $1,000
Compute ∆ IRR(1-3)
PW(∆ i') = 0 = -$4,500 + $700(P|A, ∆i'%, 10) + $1,000(P/F, ∆i'%, 10)
∆ i‘(1-3) ≈ 10.9%
Since ∆i' < MARR, keep alt. 3 (lower FC) as current best alternative. Drop alt. 1 from further consideration
Step 5. All alternatives have been considered
Recommend alternative 3 for investment
∆ cash flow
Слайд 20Study period ≠ Useful life
Up until now, study periods and useful
Repeatibility Assumption
Conditions:
Study period is either indefinitely long or equal to a common multiple of the lives of the alternative
The cash flows associated with an alternative's initial life span are representative of what will happen in succeeding life spans
Actual situations in engineering practice seldom meet these two conditions, which limits the use of the repeatability assumption
Слайд 21Example: 5-24
Cost alternative: Study period>Useful life
Given two MEAs and MARR
Hint: first draw a cash flow diagram
Слайд 22Example: 5-24 - Solution
Consider the AW over the useful life of
AW(A )= -14,000(A/P, 15, 5)- 14,000 + 8,000(A/F, 15, 5) = -16,990
Life 1: AW (1-5) = -16,990
Life 2: AW (6-10) = -14,000(A/P, 15, 5)- 14,000 + 8,000(A/F, 15, 5) = -16,990
Life 3: AW (11-15 )= -16,990
Life 4: AW (16-20) = -16,990
AW(B)= -65,000(A/P, 15, 20)- 9,000 + 13,000(A/F, 15, 20) = -19.262
AW(A )> AW(B)
Shortcut: If the study period equals a common multiple of the alternatives' lives, simply compare AW computed over the respective useful lives (assuming repeatability is valid)
Слайд 23Example: 5-24 – PW Solution based on the total study period
PW(A)
PW (B) = -65,000 - 9,000(P/A, 15, 20) + 13,000(P/F, 15, 20) = -$120,539
Select A to minimize costs
Also,
AW(A) = -$106,345(A/P, 15, 20) = -$16,990
AW(B)= -$120,539(A/P, 15, 20) = -$19,262
Слайд 24What if the study period is not a common multiple of
An appropriate study period need to be selected (coterminated assumption)
Слайд 25Study period > Useful life
Use the Cotermination Assumption
Procedure:
Case 1: Suppose study period > useful life
Cost alternatives: Since each cost alternative has to provide the same level of service over the study period, contracting for the service or leasing the needed equipment for the remaining years may be appropriate
Investment alternatives: Assume all cash flows will be reinvested at the MARR to the end of the study period (i.e., calculate FW at end of useful life and move this to the end of the study period using the MARR). PW can also be used.
See Examples 5-7 and 5-8, page 210
Слайд 26Case 2: Study period < useful life
When the study period is
Procedure: The cash flows of the alternatives need to be adjusted to terminate at the end of the study period
Truncate the alternative at the end of the study period using an estimated Market Value
Слайд 27Example: Cotermination
Useful life of A = 20 years = study period
Useful
Assume Market Value (B) @ EOY20 = $50,000
The MARR is 10% per year.
Which boiler do you recommend?
Слайд 28Example: Solution
AW(A) (10%) = -50,000(A/P,10, 20) -9,000 +10,000(A/F,10,20) = -14,700
AW(B) (10%)
Still select boiler A to minimize costs
What would the market value of Boiler B @ EOY 20 have to be in order to select Boiler B instead of A?
Слайд 29Example: Solution
Market Value of Boiler B to reverse the decision =
Set AW(A) = AW(B) , let X be the unknown market value
-14,700 = -6,000 - {120,000(A/P, 10, 20) - X(A/F,10, 20)}
-8,700 = -{14,100 - 0.0175X}
5,400 = 0.0175X
X = $308,571 therefore, MV(B) > $308,571 to favor B
Such a value is very unlikely because X is more than the initial cost of Boiler B