Будущая стоимость (FV) презентация

Содержание

Пример: если положить на срочный вклад 1000 руб. под 10% годовых, сроком на 2 года, то через 2 года это будет 1210 руб. FV= PV(1+r)2 = 1000(1+0,1)2=1210 руб.

Слайд 1Будущая стоимость (FV) – это та сумма средств, в которую вложенные

сегодня средства, превратятся через определённый период времени.
  
 
Величина будущей стоимости определяется по формуле:
FV=PV(1+r)n (1)
 
где FV-будущая стоимость
PV-текущая стоимость
r –процентная ставка
n- число лет, в течение которых деньгинаходятся в обороте

Слайд 2Пример: если положить на срочный вклад 1000 руб. под 10% годовых,

сроком на 2 года, то через 2 года это будет 1210 руб.


FV= PV(1+r)2 = 1000(1+0,1)2=1210 руб.

Слайд 3Текущая стоимость (PV) – это первоначальная сумма, которая инвестируется ради получения

дохода в будущем.
 
 
Текущая стоимость рассчитывается по формуле:
или (2)
 
 
 
В нашем примере: 1210 руб./(1+0,1)2= 1000 руб.



Слайд 4Простой процент – это сумма, которая начисляется от исходной стоимости вложения

в конце одного периода, определяемого условиями вложения (месяц, год). Применяется при краткосрочных вложениях.

Сумма простого процента (S) определяется по формуле:
S = PV· (rt · n)
где r – процентная ставка
n – количество периодов
Будущая стоимость инвестиций (FV) с учётом простых процентов определяется по формуле: 
FV=PV+S=PV(1+rt · n)
где (1+r · n) – коэффициент наращивания простых процентов.

Слайд 5При расчёте простого процента в процессе дисконтирования используется формула:

 

где

- коэффициент дисконтирования простых процентов.




Слайд 6Сложный процент - это сумма дохода, которая образуется в результате вложения

средств, при условии, что сумма начисленного простого процента не выплачивается после каждого периода, а присоединяется к сумме основного вклада и в последующем доход исчисляется с общей суммы, включающей также начисленные и невыплаченные проценты.

Применяются, как правило, при долгосрочных инвестиционных операциях.
 
Начисление сложных процентов для нахождения величины будущей стоимости в инвестиционном анализе называется – компаундингом.

Слайд 7Пример: В банк на срочный вклад положили 100 тыс.руб. на 2

года по ставке 10% годовых. Затем вклад:
а) продлевается на 1 год по ставке 8%
б) изымается и кладётся на новый счёт на 1 год по ставке 8%. Найдём наращенную за три года сумму, если проценты начисляются один раз в год.
При использовании простого процента:
а) FV=PV(1+r1 n1+ r2 n2)
FV=100 тыс.руб.(1+0,1·2+ 0,08·1)= 128 тыс.руб.
б) FV1=PV(1+r1 n1)
FV1= 100 тыс.руб.(1+0,1·2)= 120 тыс. руб.
FV2= FV1 (1+ r2 n2)
FV2= 120 тыс.руб.(1+ 0,08·1)=129,6 тыс.руб.

Слайд 8При использовании сложного процента:
 
а) FV=PV(1+r1 )n1 ( 1+ r2 )n2


FV= 100 тыс.руб.(1+0,1)2 ·(1+0,8)1=130,7 тыс.руб.
б) FV1=PV(1+r1)n1
FV1= 100 тыс.руб.(1+0,1)2= 121 тыс.руб.
FV2= FV1 (1+ r2 )n2
FV2=121 тыс.руб.(1+0,08)1= 130,7 тыс.руб.

Слайд 9Аннуитет - это равные денежные суммы, получаемые и выплачиваемые через одинаковые

промежутки времени
 
Будущая стоимость аннуитета(Sа) рассчитывается по формуле:
Sa= Σ Pа (1+r)n-t
Pа – аннуитетный платёж, осуществляемый в конце периода t;
n - количество периодов времени
r – ставка сложного процента

Слайд 10Так как все платежи являются равными по величине, будущую стоимость аннуитета

можно упростить:
  FVan = Pa · kf
 
где FVan –будущая стоимость аннуитета на конец определённого периода;
Pa - сумма аннуитетного платежа;
kf - коэффициент наращивания аннуитета;
Коэффициент наращивания аннуитета (kf) рассчитывается по формуле:



Слайд 11Пример: Для создания резервного фонда ежегодно выделяется 80 тыс.руб. Ставка процента

10%. Найти величину данного фонда через четыре года.

FVan=80 тыс.руб.[(1+0,1)4-1] /0,1 = 371,28 тыс.руб.
 
В расчёте можно применять значение коэффициента дисконтирования, которое в соответствии с таблицей (при ставке процента 10% и числе периода 4) составляет 4,641:
 
FVan=80·4,641=371,28 тыс. руб.

Слайд 12Текущая стоимость аннуитета рассчитывается по формуле:
PVan= Pa · kp
 
где

kp - коэффициент дисконтирования аннуитета:
 

данный коэффициент можно определить и по финансовым таблицам.



Слайд 13Пример: По кредитному договору общая сумма долга с процентами (из расчёта

сложной процентной ставки 20% годовых) погашается в течение пяти лет равными выплатами в размере 200 тыс.руб. Найти основную сумму долга.

PVan= 200· [1 – (1+0,2)-5] / 0,2 = 598,2 тыс.руб.
 
Используем значение коэффициента дисконтирования аннуитета в соответствии с финансовой таблицей оно при 20% ставке и числе периодов 5 равно 2,99061:
 
PVan= 200 тыс. руб. · 2,99061= 598,2 тыс.руб.

Слайд 14Инфляция – это процесс повышения среднего уровня цен в экономике и

снижение покупательной способности денег.
 
Инфляция называется равномерной, если темп общей инфляции не зависит от времени (от номера шага расчётного периода)
 
Однородная инфляция – если темпы изменения цен на товары и услуги зависят только от момента времени, а не характера товаров и услуг.
 
Инфляция постоянная если её темп не меняется со временем.

Слайд 15Номинальная стоимость денег – это оценка её величины без изменения покупательской

способности денег.

Реальная стоимость денег – это оценка с учётом изменения покупательской способности денег в силу инфляции.

Номинальная процентная ставка (rnom) – объявленная процентная ставка, учитывающая уровень инфляции.

Реальная процентная ставка (rreal)– это номинальная процентная ставка, «очищенная» от инфляции.

Текущие цены – это цены, предусмотренные в инвестиционных проектах без учёта инфляции.

Прогнозные цены – цены, ожидаемые при реализации проекта с учётом инфляции.

Слайд 16Основные показатели инфляции:
 
Темп инфляции (Ti) – характеризует прирост уровня цен в

рассматриваемом периоде.
 
Индекс инфляции (Ii)
Ii = 1+Ti

Слайд 17Будущая стоимость с учётом инфляции рассчитывается по формуле:

или

где - коэффициент наращивания, откорректированный на индекс инфляции.
Пример: Если темп инфляции 12%, а индекс инфляции соответственно 1,12, то реальная стоимость денежной суммы в 100 тыс.руб., вложенных под 15% годовых через три года составит:
FVр= 100(1+0,15)3 /1,123 = 108,25 тыс.руб.




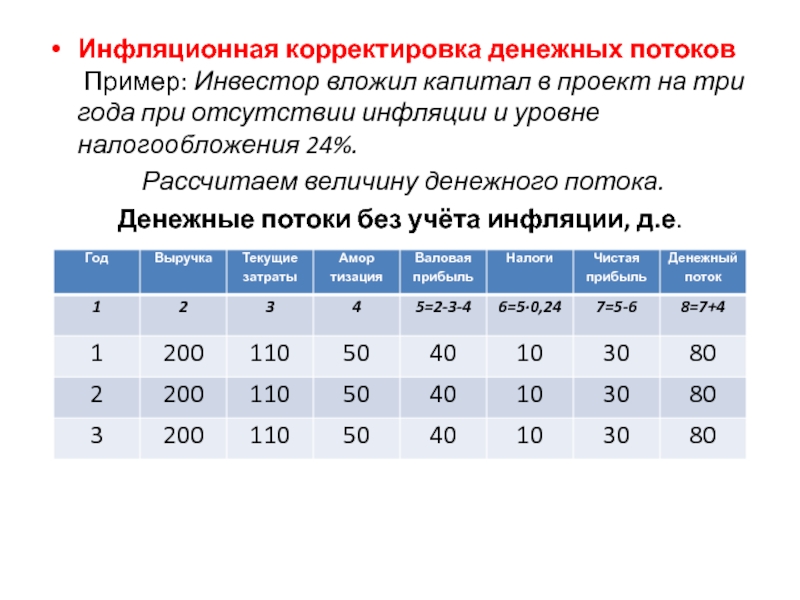
Слайд 18Инфляционная корректировка денежных потоков Пример: Инвестор вложил капитал в проект на

три года при отсутствии инфляции и уровне налогообложения 24%.
Рассчитаем величину денежного потока.
Денежные потоки без учёта инфляции, д.е.

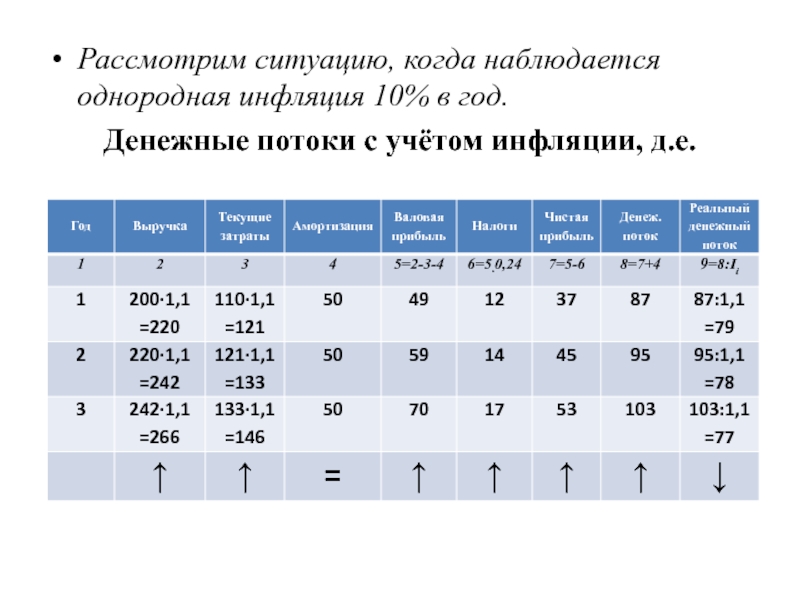
Слайд 19Рассмотрим ситуацию, когда наблюдается однородная инфляция 10% в год.
Денежные потоки с

учётом инфляции, д.е.

Слайд 20Учет реальной и номинальной процентной ставки
 
Связь между уровнем инфляции, номинальной и

реальной процентными ставками отражает формула Фишера:

1+rnom=(1+rreal)·(1+Ti)

где rnom - номинальная процентная ставка
rreal - реальная процентная ставка
Ti - темп инфляции
1+Ti -индекс инфляции
 
rnom≈ rreal + Ti



Слайд 21Пример: Номинальная ставка по банковскому кредиту составляет 14%. Годовой темп инфляции

11%. Найти реальную ставку по банковскому кредиту
 
rreal = (0,14-0,11) / (1+ 0,11) =0,027 или 2,7%

Слайд 22Анализ чувствительности в условиях высокого уровня инфляции
 
При проведении анализа

чувствительности последовательно анализируется с помощью показателей инфляции следующие виды инфляций:
- общая
- переменных издержек
- заработной платы
- основных фондов
- постоянных издержек и накладных расходов и т.д.

Слайд 23Динамические показатели основаны на применении концепции дисконтирования, учитывают весь жизненный цикл

проекта и рассчитываются с помощью методов:
чистого дисконтированного дохода
индекса доходности
внутренней нормы доходности
дисконтированного срока окупаемости.

Слайд 24 Чистый дисконтированный доход ( NPV) («чистый приведённый доход», «чистая текущая стоимость»,

«общий финансовый итог от реализации проекта».)


Чистый дисконтированный доход представляет собой превышение интегральных результатов над интегральными затратами и рассчитывается как разность дисконтированных денежных потоков доходов и расходов, производимых в процессе реализации инвестиций в течение срока жизни проекта.
 


 


Слайд 25 Алгоритм расчёта чистого дисконтированного дохода (NPV):
Подбирается норма дисконтирования, и рассчитываются соответствующие

коэффициенты дисконтирования по шагам анализируемого расчётного периода.
Определяется дисконтированная стоимость каждого денежного потока (притоков оттоков).
Суммируются все дисконтированные значения денежных потоков, и определяется величина NPV
Принимается решение:
а) для отдельного проекта:
NPV > 0, проект следует принять;
NPV <0, то проект следует отвергнуть;
NPV =0, то проект можно принять, при этом благосостояние инвестора не изменится, а масштабы предприятия увеличатся.
б) для альтернативных проектов:
сравниваются проекты, имеющие положительное значение NPV, и принимается тот, который имеет большое значение NPV .

Слайд 26Чистый дисконтированный доход является критерием экономической целесообразности инвестирования средств:
 
положительное значение

NPV показывает, что за расчётный период дисконтированные денежные поступления превышают дисконтированную сумму инвестиционных затрат и обеспечивают увеличение стоимости компании;
отрицательное значение NPV показывает, что инвестиционный проект не обеспечивает получения требуемой нормы доходности и проект является убыточным

Слайд 27Чистый дисконтированный доход для постоянной величины дисконта и разовой первоначальной инвестиции

определяют по формуле:





где I0 - величина первоначальных инвестиций
Пt –приток денежных средств в момент времени t
Ot – отток денежных средств в момент времени t
r - ставка дисконтирования
t - шаг расчёта (год, квартал, месяц)
Т – величина расчётного периода (число жизненного цикла проекта)

Слайд 28Чистый дисконтированный доход при инвестировании финансовых ресурсов в течение ряда лет,

определяют по формуле:

Слайд 29 Достоинства метода
отражает доходы инвестиций, учитывает срок жизни инвестиционного проекта, и распределение

во времени денежных потоков;
учитывает стоимость денег во времени;
показатель аддитивен, т.е. NPV различных проектов можно суммировать NPVА+ NPVВ= NPVА+В
соответствует главному критерию эффективности инвестиций.
 

Слайд 30 Недостатки
показатель абсолютный, т.е. он не учитывает размера альтернативных проектов;
зависит от величины

нормы дисконта;
ставка дисконта, обычно не изменяется для всего периода жизненного цикла проекта.

Слайд 31Пример: Компания собирается приобрести новую линию стоимостью 75 млн. руб. со

сроком эксплуатации пять лет, внедрение её позволит обеспечить ежегодные поступления в 25 млн. руб., требуемая норма доходности – 10%. Определить является ли данный проект целесообразным?


Если использовать формулу текущей стоимости аннуитета, то


Слайд 32 Индексы доходности (PI) («индексы рентабельности», «индексы прибыльности инвестиций».)
Индексы доходности характеризуют отдачу проекта

на вложенные в него средства.
 
Виды индексов:
Индекс доходности затрат
Индекс доходности дисконтированных затрат
Индекс доходности инвестиций
Индекс доходности дисконтированных инвестиций

Слайд 33Индекс доходности затрат – это отношение суммы денежных притоков к сумме

денежных оттоков.



где Пt - денежный приток на каждом шаге расчета
Оt - денежный отток на каждом шаге расчета
 

Слайд 34Индекс доходности дисконтированных затрат – отношение суммы дисконтированных денежных притоков к

сумме дисконтированных денежных оттоков.

Слайд 35Индекс доходности инвестиций – это отношение суммы элементов денежного потока от

операционной деятельности к абсолютной величине суммы элементов денежного потока от инвестиционной деятельности.


где Пt - Оt- денежные потоки по шагам расчётного периода
It - инвестиции по шагам расчёта
NPV - чистый дисконтированный доход

Слайд 36Индекс доходности дисконтированных инвестиций – отношение суммы дисконтированных элементов денежного потока

от операционной деятельности к абсолютной величине суммы дисконтированных элементов денежного потока от инвестиционной деятельности.

Слайд 37 Условия принятия инвестиционного проекта  
PI >1 - проект эффективен
PI

не эффективен
PI=1 - проект можно принять, при этом благосостояние инвестора не изменится, а масштабы предприятия увеличатся.

Слайд 38 Достоинства
относительный показатель, отражает эффективность единицы инвестиций;

позволяет судить о резерве безопасности проекта.

Слайд 39 Недостатки

не аддитивен
зависит от нормы дисконта.
 

Слайд 40Пример: Рассчитаем индекс доходности дисконтированных инвестиций, если первоначальные инвестиции (Io) равны

75 млн. руб., срок эксплуатации проекта пять лет, ежегодные денежные поступления 25 млн. руб. при норме дисконта 10%, обеспечивают величину NPV в 19,8 млн. руб.
PI = (25· 3,791) : 75 = 1,26 или
PI = 1 + (19,8 : 75) = 1,26
PI - 1,26 > 1 - проект следует принять.

Слайд 41 Внутренняя норма доходности( IRR) («внутренняя норма дисконта», «внутренняя норма прибыли», «внутренний коэффициент

эффективности», «внутренняя ставка отдачи».)

Внутренняя норма доходности характеризует уровень доходности определённого инвестиционного объекта, при которой будущая стоимость денежного потока от инвестиций равна текущей стоимости инвестируемых средств:



Внутренняя норма доходности – это такая процентная ставка ,при которой чистый дисконтированный доход равен нулю:
IRR = r, при котором NPV = 0

Слайд 42
Суть показателя в следующем:

показывает максимально доступный

уровень расходов, которые могут быть в данном проекте.

внутреннюю норму доходности можно рассматривать как минимальный гарантированный уровень прибыльности инвестиционных затрат.

Слайд 43 Способы определения внутренней нормы доходности:
1. При равномерных денежных поступлениях

в течение расчётных периодов (аннуитет) - используются справочные таблицы коэффициентов расчёта текущей стоимости для аннуитета.
Пример: Определить внутреннюю норму доходности инвестиционного проекта (IRR), если первоначальные инвестиции (Io) равны 75 млн. руб., срок эксплуатации проекта пять лет, ежегодные денежные поступления 25 млн. руб.
а) дисконтированные денежные поступления рассчитаем по текущей стоимости аннуитета как произведение ежегодных денежных поступлений на коэффициент дисконтирования аннуитета:
25 · kf
б) приравняем величины инвестиций и дисконтированных денежных поступлений: 75 = 25 · kf kf = 3
в) по финансовым таблицам найдем близкое значение для срока проекта 5 лет и kf = 3, это величина равна 2,991, ей соответствует коэффициент дисконтирования – 20%, т.е. внутренняя норма доходности (IRR) равна 20%.

Слайд 44 2. При равномерных денежных поступлениях в течение расчётного периода:
на

основе использования компьютерных программ
методом подбора, где при расчёте значения IRR, при котором NPV = 0, задаётся избранное значение нормы дисконта, в соответствии с которой рассчитывается NPV
специальными методами, например методом линейной интерполяции:



r1 – ставка дисконта, при которой NPV имеет минимальное положительное значение
r2 - ставка дисконта, при которой NPV имеет минимальное отрицательное значение
NPV1 – величина чистого дисконтированного дохода при ставке дисконта r1
NPV2 – величина чистого дисконтированного дохода при ставке дисконта r2

Слайд 45Определим внутреннюю норму доходности инвестиционного проекта методом подбора и методом линейной

интерполяции.
Первоначальные инвестиции (Io) равны 75 млн. руб., срок эксплуатации проекта пять лет, общий объём денежных поступлений-125 млн. руб. Денежные поступления поступают неравномерно: первый год – 35 млн. руб., во второй год – 30 млн. руб., в третий год – 25 млн. руб., в четвертый год – 20 млн. руб., в пятый год – 15 млн. руб.

Слайд 46Рассчитаем NPV при норме дисконта 20%:




Рассчитаем NPV при норме дисконта 23%

и 25%:


 




Примем NPV1=1,4млн. руб. за минимально положительное значение при ставке дисконта r1 = 23%, а NPV2 = -1,9 млн. руб. за минимально отрицательное значение при ставке дисконта r2 = 25%, тогда




Слайд 47Условия принятия инвестиционного проекта
IRR > r , NPV > 0

- проект эффективен
IRR < r , NPV < 0 - проект неэффективен
IRR > CC проект следует принять
IRR < CC проект следует отклонить
IRR = CC проект ни прибыльный, ни убыточный

 

Слайд 48 Достоинства

относительный показатель, не зависит от абсолютного размера инвестиций;

нацелен на увеличение

доходов инвесторов.

Слайд 49Недостатки

сложность без компьютерных расчётов

большая зависимость от точности оценки будущих денежных

потоков
 

Слайд 50
Для оценки одного проекта должны выполняться следующие соотношения:
 

если NPV > 0 IRR > r RI > 1
NPV < 0 IRR < r RI < 1
NPV = 0 IRR = r RI = 1
 
где r – требуемая норма доходности.

Слайд 51 Дисконтированный срок окупаемости
Дисконтированный срок окупаемости – это продолжительность периода

в течении которого сумма чистых денежных поступлений, дисконтированных на момент начала инвестиций, равна сумме инвестиций.
 
При неравных денежных поступлениях по годам, срок возврата инвестиций определяется методом вычитания.

Слайд 52
Пример: определить срок возврата инвестиций в размере 100 д.е., если прибыль

по проекту составляет: 1 год – 25 д.е., 2 год – 30 д.е., 3 год – 40 д.е., 4 год – 50 д.е.
 
Дисконтированный срок окупаемости (Ток):
1 год 100 д.е. - 25 д.е. = 75 д.е.
2 год 75 д.е. – 30 д.е. = 45 д.е.
3 год 45 д.е. – 40 д.е. = 5 д.е.
4 год 5 д.е. – 50 д.е. 50 д.е.
Определим за какую часть 4 года возместятся 5 д.е. 5 д.е. : 50 д.е. = 0,1 года
Ток = 3 года + 0,1 года = 3,1 года
 
 

Слайд 53 Статические методы оценки инвестиций  
срок окупаемости инвестиций (РР)
рентабельность инвестиций (АRR) (коэффициент эффективности

инвестиций, учётная норма прибыли, бухгалтерская рентабельность)
чистый доход (NV) (чистые денежные поступления, чистый денежный поток)
максимальный денежный отток (потребность в финансировании, отток денежных средств)

Слайд 54 Срок окупаемости инвестиций (РР)
Срок окупаемости- это период времени (месяц, квартал, год),

в течение которого первоначальные инвестиции, вложенные в проект полностью возмещаются доходами от его реализации.

Если не учитывать фактор времени (то есть равные суммы дохода, получаемые в разное время, рассматриваются как равноценные), то срок окупаемости определяется по формуле:


где РР – срок окупаемости
– общая сумма инвестиций в проекте
П – средняя за период жизни проекта чистая прибыль

Слайд 55Пример: Определить срок возврата инвестиций в размере 100 тыс. д.е., если

средняя прибыль по проекту 40 тыс. д.е.

Слайд 56
Инвестиционный проект считается приемлемым, если расчётный уровень срока окупаемости не превышает

величину, принятую инвестором за базовую или нормативную:
 
PPр ≤ PPн
 
Предпочтение отдаётся проектам с наименьшим сроком окупаемости. Срок окупаемости не должен превышать срока жизни проекта.

Слайд 57 Достоинства
простота использования и расчетов
 
позволяет судить о ликвидности проекта, так как

длительный срок окупаемости означает пониженную ликвидность
 
позволяет судить о рискованности проекта, так как длительный срок окупаемости означает высокий риск.

Слайд 58 Недостатки
игнорирует денежные поступления (доходы) после истечения срока окупаемости
 
ничего не говорит об

эффективности проекта, позволяет судить только о его ликвидности

Слайд 59 Рентабельность инвестиций (АRR)
Рентабельность инвестиций (АRR) - это отношение величины прибыли к

величине инвестиций:

Слайд 60 Варианты расчёта ARR
1. Рентабельность инвестиций (ARR) определяется как отношение годовой прибыли

до налоговых и процентных платежей (EBIT) к средней величине активов, которые будут созданы в результате инвестирования.
 
(1)

Величина инвестиций (I) находится как среднее между стоимостью активов на начало и конец реализации проекта:
 


Слайд 612. Рентабельность инвестиций (ARR) определяется как отношение годовой прибыли после налоговых

и процентных платежей [EBIT ·(1- h)] к средней величине активов, которые будут созданы в результате инвестирования
 


где EBIT – доход до процентных и налоговых платежей
h - ставка налогообложения
с - стоимость активов на начало и конец реализации проекта.
Инвестиционный проект считается приемлемым, если расчетный уровень рентабельности превышает величину рентабельности принятую инвестором за базовую.
 


Слайд 623. Рентабельность инвестиций (ARR) определяется как отношение среднегодовой чистой прибыли (П)

к сумме первоначальных инвестиций (Io)
 

Показатель рентабельности инвестиций, рассчитанный по формулам (1-3) имеет разное значение, поэтому при разработке или анализе инвестиционного проекта, необходимо уточнить по какой методике он рассчитывался.

Слайд 63Пример: Компания планирует закупить технологическую линию стоимостью 1000 д.е.со сроком эксплуатации

10 лет. Это принесёт дополнительный доход до уплаты налогов и процентов – 200 д.е. По истечению срока эксплуатации продажа линии не планируется. Ставка налогообложения 24%, доходность до закупки линии составляла 20%. Определить целесообразность закупки данной линии.
 

30,4% > 20%, т.е. инвестиции эффективны.
 


Слайд 642. Если расчёт рентабельности инвестиций ведется как отношение прибыли не какого-то

определённого года, а её средней величины (за вычетом амортизации) к первоначальным инвестициям, то
 


где ЧП – чистая прибыль
А – амортизационные отчисления
Двнер.- внереализационные поступления (% по ценным бумагам)

 
где В – выручка от реализации
З – затраты производства
ФИ – финансовые издержки (например, % за кредит)

Слайд 65Пример: в нашем примере, приобретение линии планируется за счёт кредита под

8% годовых.
ФИ = 1000д.е. · 0,08 = 80 д.е.
Величина амортизационных отчислений за год (А) = 1000д.е.: 10 лет = 100 д.е.
ЧП = (EBIT – ФИ) ·(1 - h) = (200 - 80) · (1-0,24)=91,2д.е.
 


Слайд 66 Достоинства
простота понимания
несложные вычисления
расчет по данным бухгалтерского учёта
оценка прибыльности проекта.

Слайд 67 Недостатки
не учитывает разноценности денежных средств во времени
сложно выбрать год, характерный для

проекта
учитывает чистую прибыль, а не денежный поток 
нельзя определить лучший проект при одинаковой рентабельности, но различных инвестициях

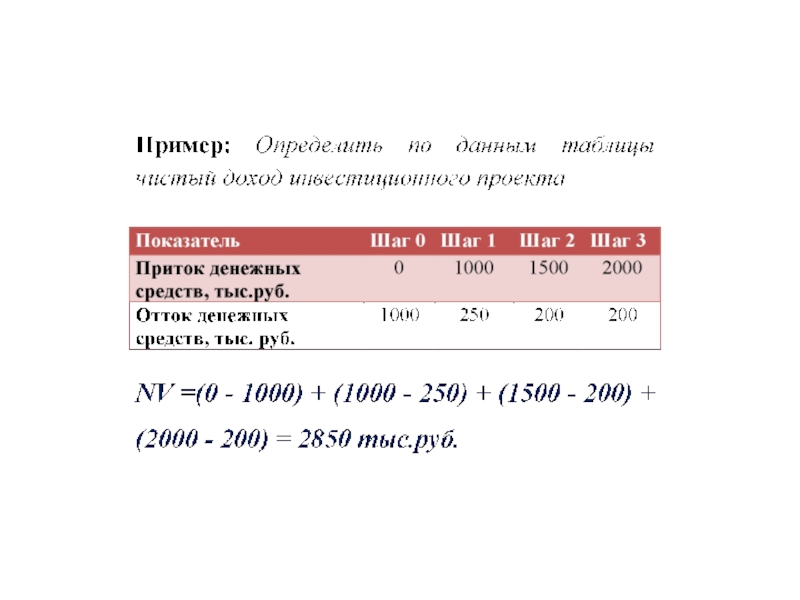
Слайд 68 Чистый доход (NV)
Чистый доход (NV) – это накопленный эффект (сальдо денежного

потока) за расчетный период.


 
где Пt - приток денежных средств
Ot – отток денежных средств
T - горизонт расчёта
t - шаг расчёта

Слайд 70 Максимальный денежный отток
Максимальный денежный отток – представляет собой максимальное значение абсолютной

величины отрицательного накопленного сальдо от инвестиционной и операционной деятельности.
 
Его величина показывает объём внешнего финансирования проекта, необходимого для обеспечения его финансовой результативности.
 

Похожие презентации

Денежный рынок 220
3 Stocks That Could Make Huge Moves This Week 208
Банкротство физических лиц 912
Тема: Практические основы кредита. Использование различных методов расчета ежемесячных платежей. 352
Размер фирмы и инвестиции в регионе 223
Финансы и Лизинг 218

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика