- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Nauczanie Łamigłówkowe презентация
Содержание
- 1. Nauczanie Łamigłówkowe
- 2. MODELOWANIE: POMYŚLMY O PROBLEMIE TROCHĘ WIĘCEJ Rozdział #3:
- 3. Zagadka 3.2 Stoisz przy drzwiach, prowadzących do
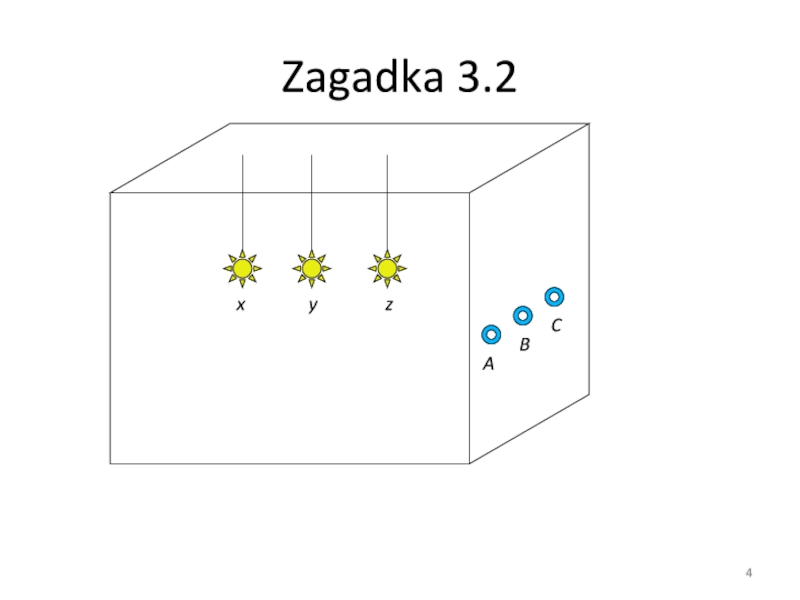
- 4. Zagadka 3.2
- 5. Zagadka 3.2 Przełączniki: Możliwe ustawienia:
- 6. Ważne spostrzeżenie Rozwiązywanie problemów świata rzeczywistego jest
- 7. Zagadka 3.3 Jest sobie podkowa z sześcioma
- 8. Reguła #3 Dokładne obliczenia i rozumowanie będą
- 9. Zagadka 3.1 Pewne przedsiębiorstwo produkcyjne ma w
- 10. Zagadka 3.1 Pytanie brzmi: ile krzeseł
- 11. Zagadka 3.1 Stosując regułę #3, możemy skonstruować
- 12. Zagadka 3.1 Cel: maksymalizacja wartości: 20$ x
- 13. Zagadka 3.1 Ograniczenia: wyprodukowanie krzesła wymaga jednej
- 14. Zagadka 3.1 Model: formalny, matematyczny model
- 15. Zagadka 3.1 Rozwiązanie: może to nie takie
- 16. Zagadka 3.1 Jednak przy rozwiązywaniu tego typu
- 17. Mapa – model świata rzeczywistego Weźmy „idealną”
- 18. Mapa – model świata rzeczywistego
- 19. Dobry model Dobry model – dostatecznie dokładny,
- 20. Model – kwestie do rozważenia Jak dokładny
- 21. Krzesła i stoły Czy ten model dałoby
- 22. Zagadka 3.4 Pani Brązowa obchodziła urodziny i jeden
- 23. Zagadka 3.4 x: wiek pani Brązowej, y:
- 24. Zagadka 3.4 x: wiek Pani Brązowej, y:
- 25. Obserwacja W 1579 François Viète zapoczątkował używanie
- 26. Pieniądze i procenty Jan odziedziczył po zmarłym
- 27. Pieniądze i procenty Julia odziedziczyła x. Jan
- 28. Znaczenie modeli w życiu codziennym Znacznie mniej
- 29. Znaczenie modeli w życiu codziennym Prosty probabilistyczny
- 30. Znaczenie modeli w życiu codziennym Wiele osób
- 31. Znaczenie modeli w życiu codziennym Proste modele
- 32. Znaczenie modeli w życiu codziennym Zbudujmy prosty
- 33. Znaczenie modeli w życiu codziennym Prawdopodobieństwo wyśnienia
- 34. Znaczenie modeli w życiu codziennym Prawdopodobieństwo wyśnienia
- 35. Znaczenie modeli w życiu codziennym Wniosek 2:
- 36. Znaczenie modeli w życiu codziennym Zbiegi okoliczności
- 37. Znaczenie modeli w życiu codziennym Kluczowa umiejętność:
- 38. Znaczenie modeli w życiu codziennym Przykład: Sekwencja
- 39. Znaczenie modeli w życiu codziennym Przykład: Sekwencja
- 40. Znaczenie modeli w życiu codziennym Przykład: Sekwencja
- 41. Znaczenie modeli w życiu codziennym Przykład: Sekwencja
- 42. Znaczenie modeli w życiu codziennym Inny (pouczający)
- 43. Znaczenie modeli w życiu codziennym Fliess uważał,
- 44. Znaczenie modeli w życiu codziennym Freud był
- 45. Pamiętaj o regule #3 Dokładne obliczenia i
- 46. Praca domowa #3a Cena biletu do parku
- 47. Praca domowa #3b Abacki, Babacki i Cabacki
- 48. Zagadka 3.2 Stoisz przy drzwiach, prowadzących do
- 49. Zagadka 3.2 Rozwiązanie: wzbogacenie standardowego modelu (włączony/wyłączony)
- 50. Zagadka 3.3 Jest sobie podkowa z sześcioma
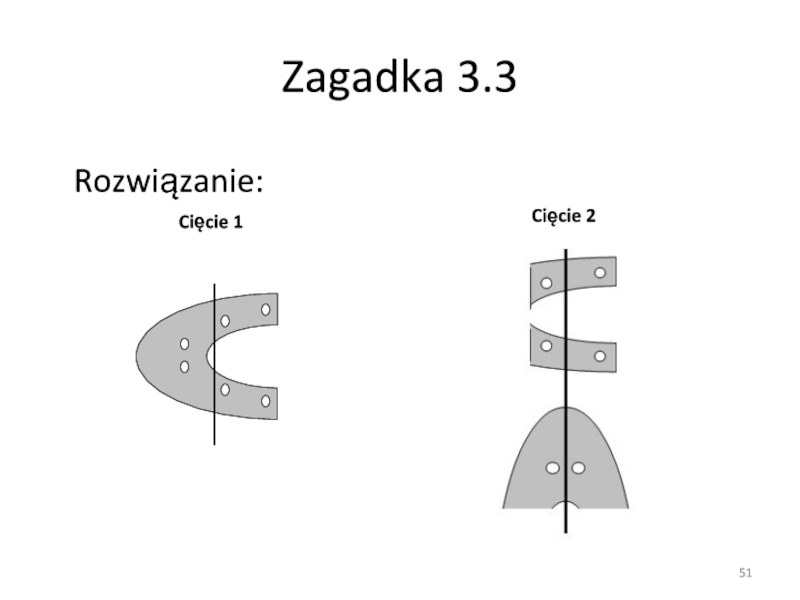
- 51. Zagadka 3.3 Rozwiązanie: Cięcie 1 Cięcie 2
Слайд 3Zagadka 3.2
Stoisz przy drzwiach, prowadzących do pustego pokoju, w którym u sufitu
Слайд 5Zagadka 3.2
Przełączniki: Możliwe ustawienia:
A 1 1 1 1 0 0 0 0
B 1 1 0 0 1 1 0 0
1 – włączony, 0 – wyłączony
Jak ustalić, który przełącznik jest podłączony do której żarówki?
Rozwiązanie pod koniec wykładu.
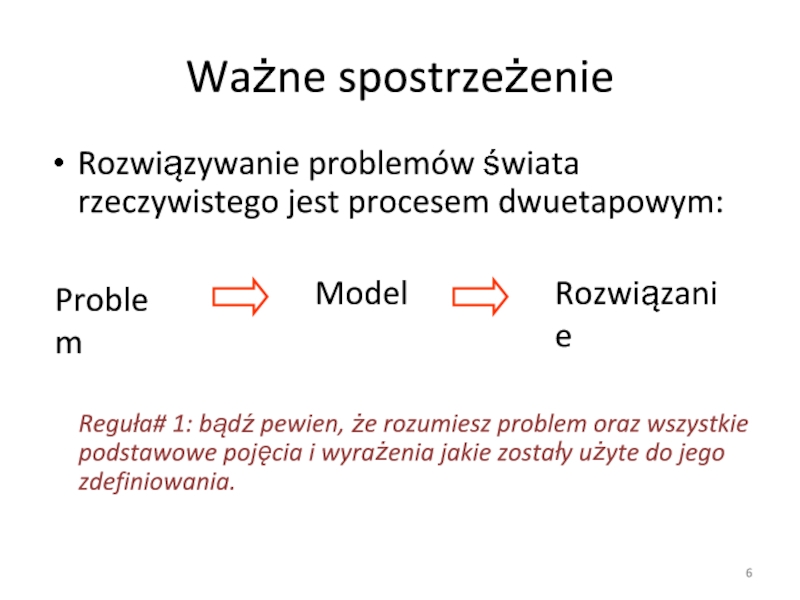
Слайд 6Ważne spostrzeżenie
Rozwiązywanie problemów świata rzeczywistego jest procesem dwuetapowym:
Reguła# 1: bądź pewien,
Problem
Model
Rozwiązanie
Слайд 7Zagadka 3.3
Jest sobie podkowa z sześcioma otworami na gwoździe:
Wykonaj dwa prostoliniowe
Rozwiązanie pod koniec wykładu.
Слайд 8Reguła #3
Dokładne obliczenia i rozumowanie będą bardziej konstruktywne, jeśli zbudujesz model
Слайд 9Zagadka 3.1
Pewne przedsiębiorstwo produkcyjne ma w ofercie tylko dwa produkty: krzesła
zysk ze sprzedaży krzesła wynosi 20$.
zysk ze sprzedaży stołu 30$.
Wyprodukowanie krzesła wymaga jednej sztuki drewna i trzech roboczogodzin, zaś wyprodukowanie stołu wymaga sześciu sztuk drewna i jednej roboczogodziny.
Proces produkcji ma pewne ograniczenia:
W procesie produkcyjnym mamy pewne ograniczenia: wszystkie maszyny mogą przetworzyć 288 sztuk drewna dziennie, a liczba dostępnych każdego dnia roboczogodzin wynosi 99.
Слайд 10Zagadka 3.1
Pytanie brzmi:
ile krzeseł i stołów powinna produkować firma, aby
Zacznijmy od zbudowania modelu…
Слайд 11Zagadka 3.1
Stosując regułę #3, możemy skonstruować model problemu, określając następujące jego
Zmienne: są tylko dwie zmienne, x i y odpowiadające liczbie produkowanych krzeseł i stołów.
Ograniczenia: są dwa ograniczenia produkcji na dobę:
288 przetważanych jednostek drewna
99 roboczogodzin.
Cele: w tym konkretnym przypadku jedynym celem jest maksymalizacja zysku.
Слайд 12Zagadka 3.1
Cel:
maksymalizacja wartości: 20$ x + 30$ y
Np. jeśli firma będzie
20$ × 10 + 30$ × 15 = 200$ + 450$ = 650$.
Oczywiście im więcej wyprodukujemy krzeseł i stołów tym zysk będzie większy, np. jeżeli zamiast 15 wyprodukujemy 20 stołów (tj. y = 20), to dzienny zysk będzie wynosił:
20$ × 10 + 30$ × 20 = 200$ + 600$ = 800$.
Слайд 13Zagadka 3.1
Ograniczenia:
wyprodukowanie krzesła wymaga jednej sztuki drewna i trzech roboczogodzin
wyprodukowanie
wszystkie maszyny mogą przetworzyć 288 sztuk drewna dziennie
x + 6y ≤ 288 (drewno)
liczba dostępnych każdego dnia roboczogodzin wynosi 99.
3x + y ≤ 99 (praca)
Слайд 14Zagadka 3.1
Model:
formalny, matematyczny model zadania maksymalizacji zysku przedsiębiorstwa może być
maksymalizacja wartości: 20$ x + 30$ y
Przy ograniczeniach:
x + 6y ≤ 288
3x + y ≤ 99
gdzie x ≥ 0 i y ≥ 0 i gdzie wartości obydwu zmiennych mogą przyjmować wyłącznie wartości całkowite.
Слайд 15Zagadka 3.1
Rozwiązanie:
może to nie takie oczywiste na pierwszy rzut oka, ale…
x
co daje zysk w wysokości 1710$.
To najlepszy plan jaki możemy przyjąć – każda inna para liczb (inna liczba krzeseł i stołów) da mniejszy zysk.
Dojście do rozwiązania na kolejnych wykładach.
Слайд 16Zagadka 3.1
Jednak przy rozwiązywaniu tego typu zadania zawsze należy sobie zadać
Czy ten model jest adekwatny do postawionego problemu?
Czy zawarliśmy w nim wszelką istotną informację?
Zawsze można stworzyć więcej niż jeden model dla problemów świata rzeczywistego.
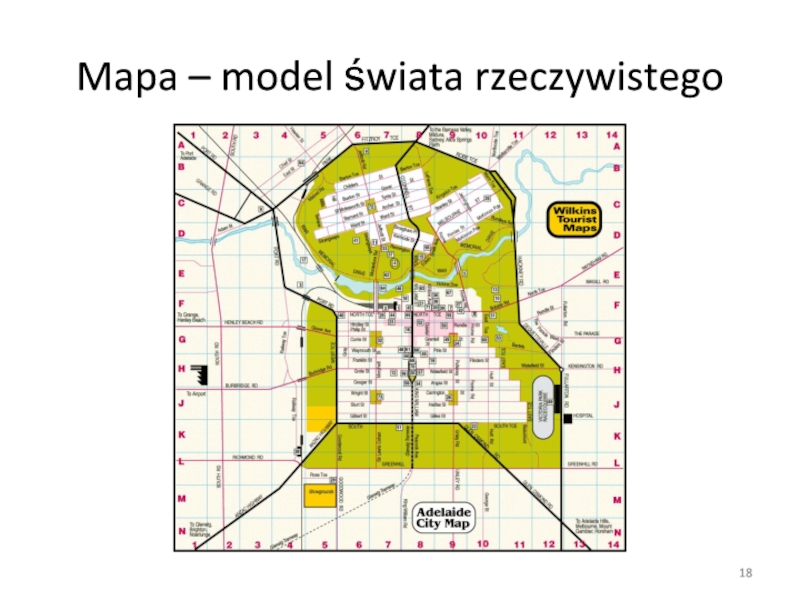
Слайд 17Mapa – model świata rzeczywistego
Weźmy „idealną” mapę dla dowolnego dużego miasta
Слайд 19Dobry model
Dobry model – dostatecznie dokładny, aby wygenerować sensowne, konkretne rozwiązania,
Dobry model powinien spełniać dwa intuicyjne wymagania:
powinien być na tyle ogólny, aby informacje i cechy nieistotne dla rozwiązania problemu zostały zakryte
powinien być na tyle szczegółowy, aby mógł dać sensowne rozwiązanie.
Слайд 20Model – kwestie do rozważenia
Jak dokładny jest model (oceniając w ramach
Jak trudno jest znaleźć rozwiązanie w przyjętym modelu?
Jak oceniany jest kompromis między precyzją modelu, a jakością i przydatnością zwracanych rozwiązań?
Jak często model będzie używany?
Ile czasu zajmuje przeciętnie znalezienie rozwiązania?
Jaki jest koszt zastosowania znalezionego rozwiązania?
Слайд 21Krzesła i stoły
Czy ten model dałoby się zastosować w świecie rzeczywistym?
maksymalizacja
Przy ograniczeniach:
x + 6y ≤ 288
3x + y ≤ 99
gdzie x ≥ 0 i y ≥ 0 i gdzie wartości obydwu zmiennych mogą przyjmować wyłącznie wartości całkowite.
Слайд 22Zagadka 3.4
Pani Brązowa obchodziła urodziny i jeden z gości zapytał ją o
Ile lat ma pani Brązowa?
Слайд 23Zagadka 3.4
x: wiek pani Brązowej, y: wiek pana Brązowego
Suma wieku pani
Pan Brązowy ma dwa razy tyle lat, ile miała pani Brązowa, kiedy pan Brązowy miał tyle lat, co pani Brązowa teraz :
y = 2(x – (y – x))
(y – x) lat temu pan Brązowy miał tyle lat, co pani Brązowa teraz
y > x
x + y = 140
W tamtym czasie pani Brązowa miała x – (y – x) lat
Слайд 24Zagadka 3.4
x: wiek Pani Brązowej, y: wiek Pana Brązowego
y = 2(x
x + y = 140
{
Łatwe rozwiązanie:
x = 60
y = 80
Pani Brązowa obchodziła sześćdziesiąte urodziny.
Слайд 25Obserwacja
W 1579 François Viète zapoczątkował używanie symboli algebraicznych – x, y,
Prosta, ponad 400-letnia idea, której nadal niektórzy nie potrafią pojąć: niech x będzie wartością nieznaną, której szukamy; zapisz warunki zadania w postaci równania z niewiadomą x, a następnie rozwiąż je, tym samym otrzymując szukaną wartość.
Слайд 26Pieniądze i procenty
Jan odziedziczył po zmarłym stryju 25% procent więcej pieniędzy
Jaki procent swoich pieniędzy powinien Jan przekazać siostrze?
Слайд 27Pieniądze i procenty
Julia odziedziczyła x.
Jan odziedziczył 1.25 x.
Powinien dać jej 0.125
0.125 x to 10% wartości 1.25 x, czyli Jan powinien dać Julii 10% swojej części pieniędzy.
Слайд 28Znaczenie modeli w życiu codziennym
Znacznie mniej osób obawia się wypadku samochodowego
Prosty model (statystyki z 1985, USA):
45,000 zabitych w wypadkach samochodowych,
17 zabitych przez terrorystów.
Слайд 29Znaczenie modeli w życiu codziennym
Prosty probabilistyczny model pozwoli zobaczyć te dane
1 : 1,600,000 – bycia zabitym przez terrorystę,
1 : 68,000 – zakrztuszenia się na śmierć,
1 : 75,000 – zgonu w wypadku rowerowym,
1 : 20,000 – utonięcia,
1 : 5,300 – zgonu w wypadku samochodowym
Слайд 30Znaczenie modeli w życiu codziennym
Wiele osób nadinterpretowuje „niezwykłe” związki postaci:
Krzysztof Kolumb
Sekretarka prezydenta Kennedy’ego nazywała się Lincoln, natomiast sekretarka prezydenta Lincolna nazywała się Kennedy.
Każde słowo w imieniu Ronald Wilson Reagan (były prezydent USA) ma 6 liter (stąd skojarzenie z “666”).
Znany pisarz Mark Twain urodził się w 1835 roku, w dniu w którym pojawiła się na niebie kometa Halleya, a zmarł w 1910 roku, w dniu ponownego pojawienia się komety w pobliżu Ziemi.
Życia Thomasa Jeffersona i Johna Adamsa, dwóch ojców-założycieli Stanów Zjednoczonych, którzy mieli wielki wkład w powstanie i podpisanie Deklaracji Niepodległości 4 lipca 1776 roku, zakończyły się w tym samym dniu. Obaj zmarli 4 lipca 1826 roku, dokładnie w 50 lat po podpisaniu najważniejszego dokumentu w dziejach USA.
Слайд 31Znaczenie modeli w życiu codziennym
Proste modele mogą nas chronić przed tendencją
Ilu z nas miało jakąś ciocię, babcię lub kuzynkę, której przyśnił się poważny wypadek samochodowy z udziałem przyjaciela lub bliskiego krewnego, a kilka godzin później taki wypadek faktycznie się zdarzył?
Слайд 32Znaczenie modeli w życiu codziennym
Zbudujmy prosty model.
Załóżmy, że prawdopodobieństwo tzw. proroczego
Oznacza to, że takie zdarzenie jest niezwykle rzadkie – szanse na „nieproroczy” sen są jak 9999 do 10000.
Ponadto przyjmijmy, ze sny są zdarzeniami niezależnymi, tzn. że wystąpienie bądź nie snu proroczego jednego nie dnia, nie ma żadnego wpływu na wystąpienie bądź nie snu proroczego następnego dnia.
Te założenia są ważne dla modelu, który zamierzamy zbudować.
A teraz policzmy…
Слайд 33Znaczenie modeli w życiu codziennym
Prawdopodobieństwo wyśnienia jednego „nieproroczego” snu wynosi:
0.9999
Prawdopodobieństwo wyśnienia
0.9999 × 0.9999
Prawdopodobieństwo wyśnienia trzech kolejnych „nieprorocznych” snów wynosi:
0.9999 × 0.9999 × 0.9999
(zasada mnożenia prawdopodobieństw zdarzeń niezależnych)
Слайд 34Znaczenie modeli w życiu codziennym
Prawdopodobieństwo wyśnienia n „nieproroczych” snów wynosi:
0.9999n
Jeżeli ktoś
0.9999365 ≈ 0.964
Wniosek 1: Około 96.4% ludzi, którzy śnią każdej nocy, nie będzie miało żadnego proroczego snu przez cały rok.
Слайд 35Znaczenie modeli w życiu codziennym
Wniosek 2: Około 3.6% ludzi, którzy śnią
3.6% przekłada się na miliony ludzi na świecie…
Zwróćmy też uwagę, że nawet zmniejszając prawdopodobieństwo wystąpienia proroczego snu do poziomu 1 : 1000 000, liczba osób, którym proroczy sen może się przytrafić jest nadal całkiem pokaźna.
Слайд 36Znaczenie modeli w życiu codziennym
Zbiegi okoliczności zdarzają się na świecie dużo
Kluczowa umiejętność: odróżnianie zdarzeń specyficznych od powszechnych.
Jakie jest prawdopodobieństwo, że w grupie słuchaczy są dwie osoby, które mają urodziny tego samego dnia?
Jakie jest prawdopodobieństwo, że w gupie jest druga osoba, która obchodzi urodziny 24 stycznia?
Слайд 37Znaczenie modeli w życiu codziennym
Kluczowa umiejętność: odróżnianie zdarzeń specyficznych od powszechnych.
Jeżeli
Слайд 38Znaczenie modeli w życiu codziennym
Przykład:
Sekwencja pierwszych liter nazw kolejnych miesięcy –
JFMAMJJASOND
Слайд 39Znaczenie modeli w życiu codziennym
Przykład:
Sekwencja pierwszych liter nazw kolejnych miesięcy –
JFMAMJJASOND
Слайд 40Znaczenie modeli w życiu codziennym
Przykład:
Sekwencja pierwszych liter nazw kolejnych miesięcy –
JFMAMJJASOND
Sekwencja pierwszych liter nazw planet – w języku angielskim:
MVEMJSUNP
Слайд 41Znaczenie modeli w życiu codziennym
Przykład:
Sekwencja pierwszych liter nazw kolejnych miesięcy –
JFMAMJJASOND
Sekwencja pierwszych liter nazw planet – w języku angielskim:
MVEMJSUNP
Слайд 42Znaczenie modeli w życiu codziennym
Inny (pouczający) przykład… ☺
Jeden z przyjaciół Zygmunta
Слайд 43Znaczenie modeli w życiu codziennym
Fliess uważał, że dwie liczby 23 i
Zauważył on, że te dwie liczby, 23 i 28, mają „szczególną” własność: dodanie do siebie ich wielokrotności pozwala na uzyskanie dowolnej liczby całkowitej, np.:
21 = 7 × 23 + (−5 × 28)
Слайд 44Znaczenie modeli w życiu codziennym
Freud był pod tak wielkim wrażeniem tego
Fakt: tę „szczególną” własność mają dwie dowolne liczby względnie pierwsze (np. 21 i 25)…
A Freud zmarł w wieku 83 lat…
Слайд 45Pamiętaj o regule #3
Dokładne obliczenia i rozumowanie będą bardziej konstruktywne, jeśli
Слайд 46Praca domowa #3a
Cena biletu do parku rozrywki została obniżona; w rezultacie
O jaki procent została zredukowana cena biletu?
Zbuduj model tego problemu, wskaż istotne zmienne i podaj równania, które doprowadzą do rozwiązania.
Слайд 47Praca domowa #3b
Abacki, Babacki i Cabacki postanowili we własnym gronie rozegrać
Zawody zakończyły się i w żadnej z dyscyplin nie było remisów. Abacki zdobył 22 punkty, natomiast Babacki i Cabacki zebrali po 9 punktów każdy. Babacki wygrał skok w dal. Kto był drugi w wyścigu na 400 metrów?
Zbuduj model tego problemu, wskaż istotne zmienne i podaj równania, które doprowadzą do rozwiązania.