- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические показатели презентация
Содержание
- 1. Статистические показатели
- 2. Статистический показатель - количественно-качественная обобщающая характеристика какого-либо свойства
- 3. Типы показателей Первичные (объемные, экстенсивные) Вторичные (производные,
- 4. Абсолютные показатели характеризуют абсолютные размеры явлений (масса,
- 5. Относительные показатели
- 6. Относительные показатели - результат деления двух абсолютных
- 7. Относительные показатели - сравнение двух одноименных абсолютных показателей
- 8. Относительные показатели - сравнение двух разноименных абсолютных показателей
- 9. Относительные показатели Виды относительных показателей Динамики (ОПД)
- 10. ОП динамики Для ряда динамики X1 …
- 11. ОП динамики Объем пр-ва
- 12. ОП плана и его выполнения Для ряда
- 13. ОП структуры и координации Для набора показателей
- 14. ОП структуры и координации Структура ВВП РФ
- 15. ОП интенсивности ОПИ = (характеристика явления А)
- 16. ОП сравнения Отношение одноименных абсолютных показателей, характеризующих
- 17. Средние величины
- 18. Средняя величина - обобщенный показатель, характеризующий типический уровень
- 19. Принципы применения Для погашения индив. различий Расчет
- 20. Виды средних величин Структурные Степенные Гармоническая m =
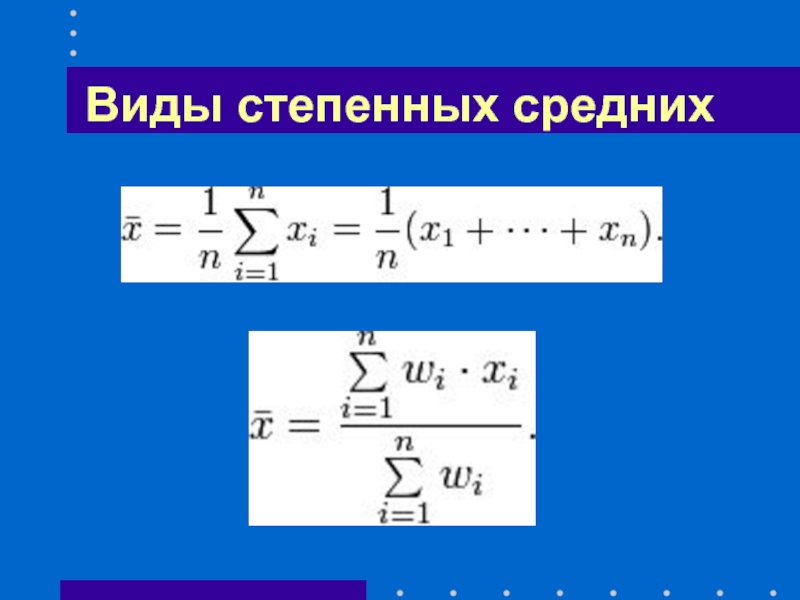
- 21. Виды степенных средних Простые Взвешенные
- 22. Виды степенных средних
- 23. Виды степенных средних Пример. Имеются данные о
- 24. Виды степенных средних Пример. Имеются данные о
- 25. Пример 1 (выбор типа средней) Какова средняя
- 26. Пример 2 (выбор типа средней) Какова средняя
- 27. Пример 3 (выбор типа средней) Какова средняя
- 28. Геометрическая средняя и ОПД Объем пр-ва
- 29. Структурные средние Мода (наиболее частое значение) Медиана
- 30. Пример: структурные средние Группы Себе- Число Объем Затраты пред- стоимость пред- прод. на пр-во приятий (т.руб.) прият. (%) (млн.р.)
- 31. Расчет моды Мо = ХМо + hМо
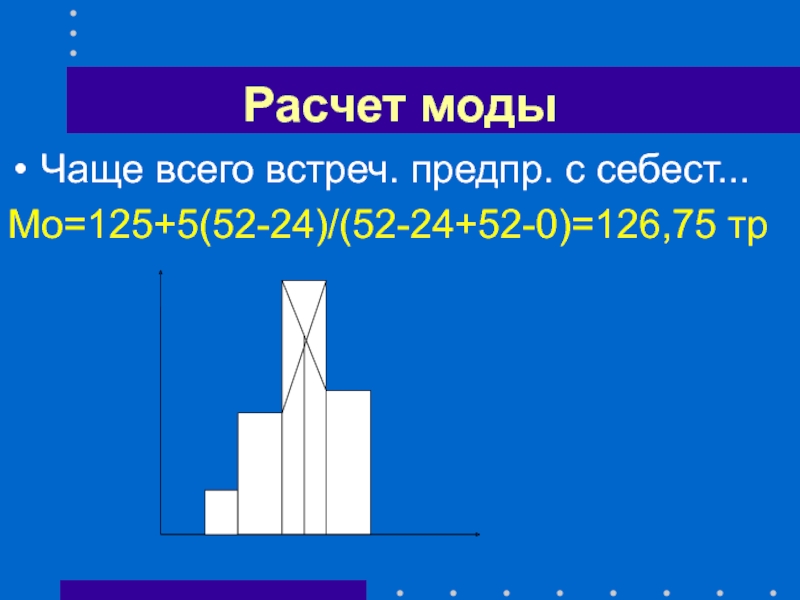
- 32. Расчет моды Чаще всего встреч. предпр. с себест... Мо=125+5(52-24)/(52-24+52-0)=126,75 тр
- 33. Расчет медианы Ме = ХМе + hМе
- 34. Расчет медианы 1/2 объема пр-ва с ур. себест. выше... Ме =120+5(50-27)/24=124,79 т.руб.
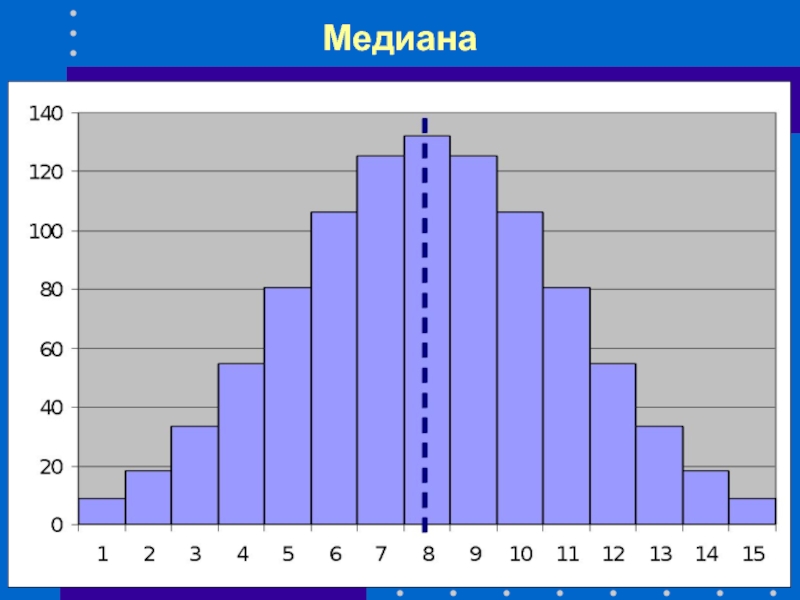
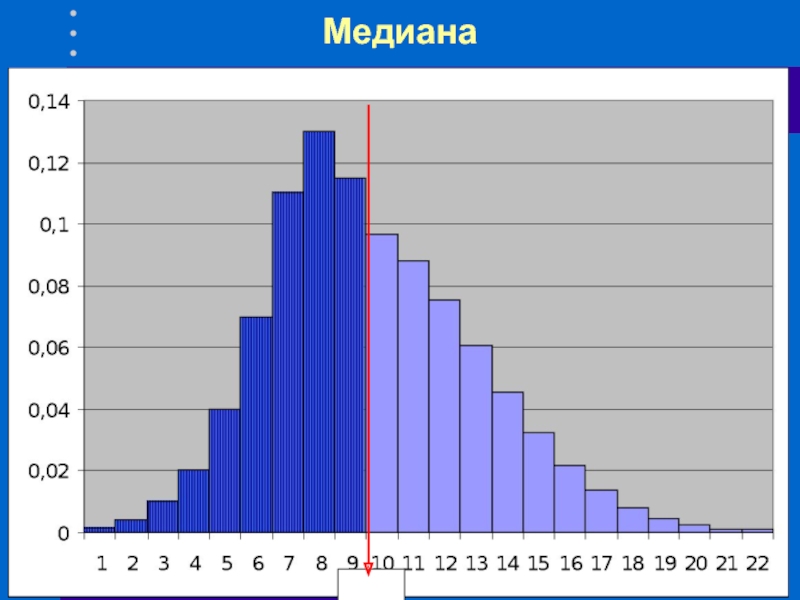
- 35. Медиана
- 36. Медиана
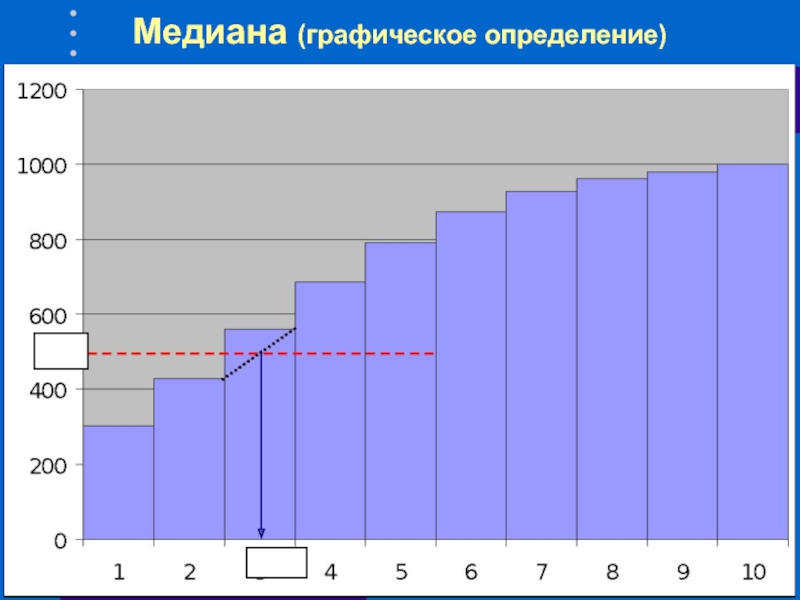
- 37. Медиана (графическое определение)
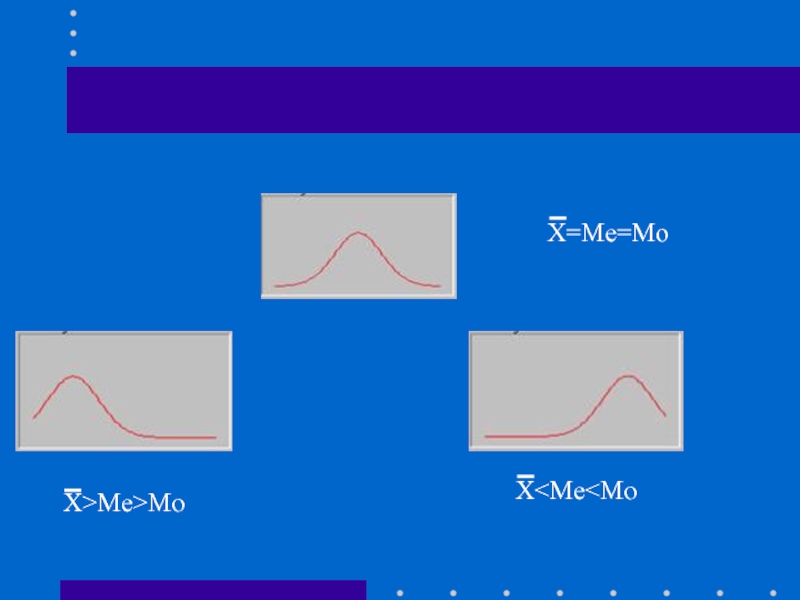
- 38. X=Me=Mo X>Me>Mo X
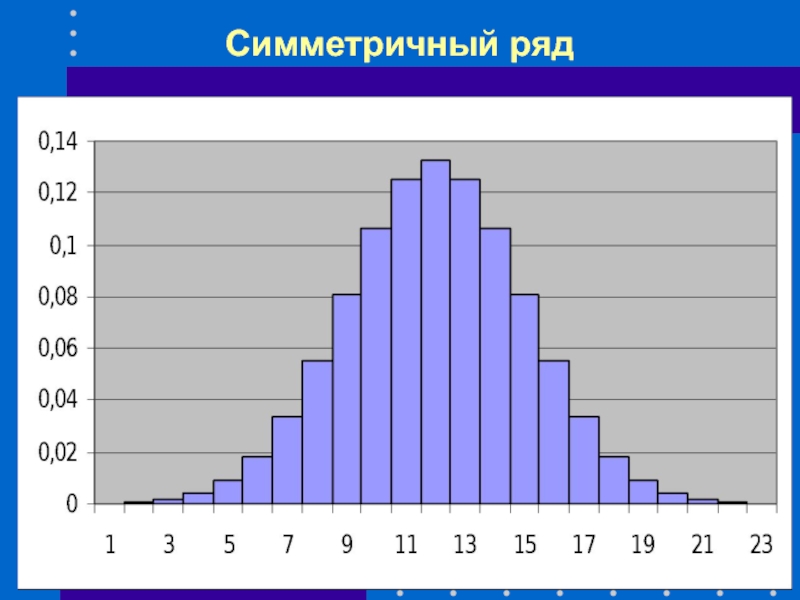
- 39. Симметричный ряд
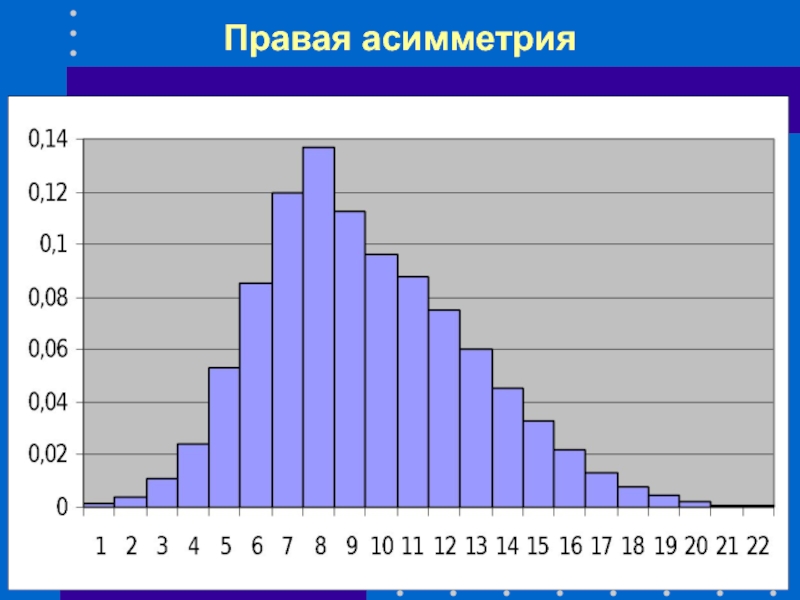
- 40. Правая асимметрия
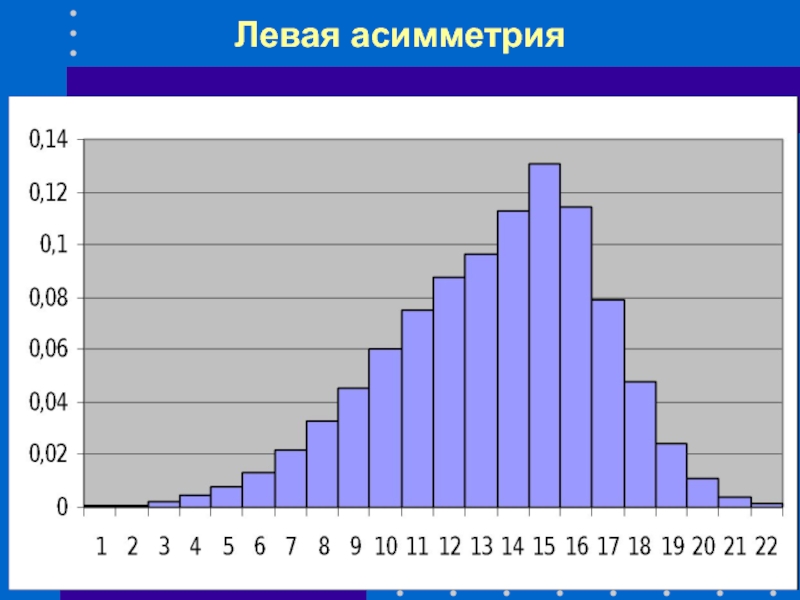
- 41. Левая асимметрия
- 42. Показатели вариации
- 43. Вариация - различие в значениях показателя у разных
- 44. Показатели вариации Размах вариации Среднее линейное отклонение Дисперсия Среднее квадратическое отклонение Коэффициент вариации
- 45. Размах вариации R = Xmax - Xmin
- 46. Среднее линейное отклонение Для несгруппированных данных d
- 47. Дисперсия Простая дисперсия для несгруппированных данных
- 48. Дисперсия Вычисление через моменты σ 2 = X2 _ X 2
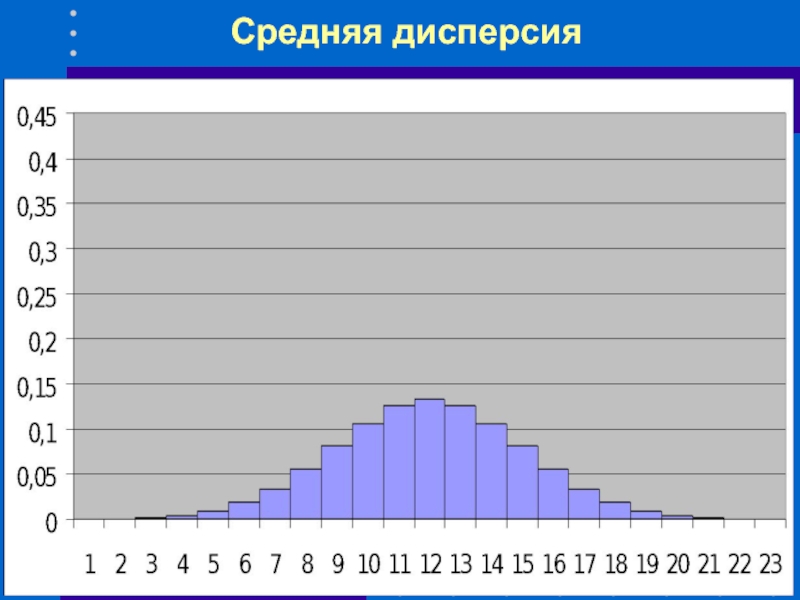
- 49. Средняя дисперсия
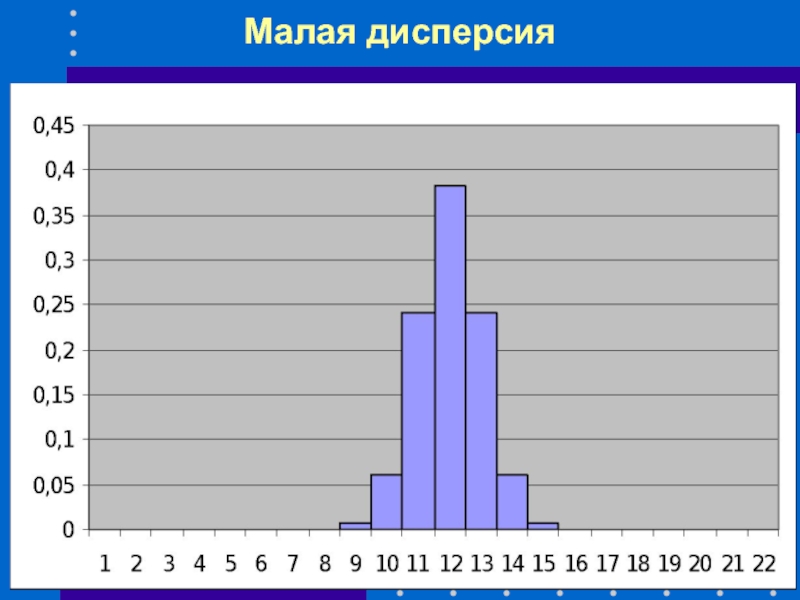
- 50. Малая дисперсия
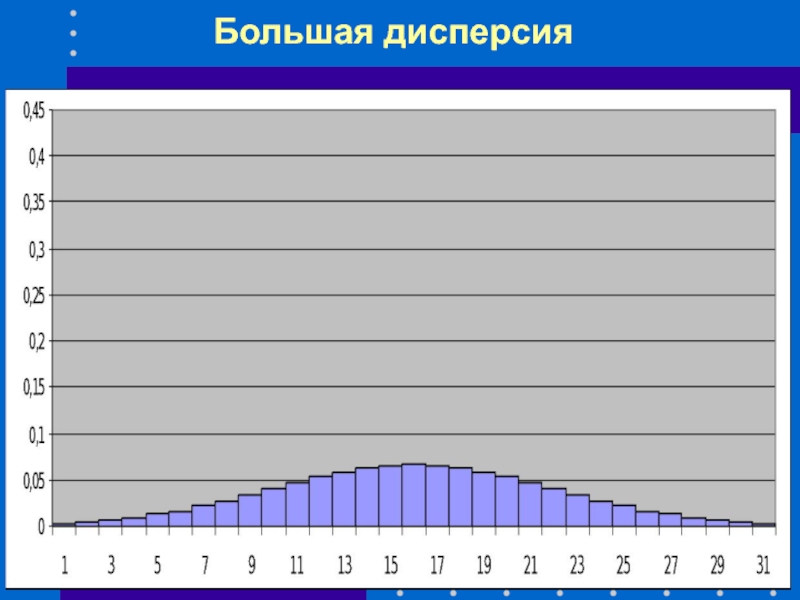
- 51. Большая дисперсия
- 52. Среднее квадратическое откл. σ = (σ 2)1/2
- 53. Коэффициент вариации V = (σ / X)
Статистический показатель - количественно-качественная обобщающая характеристика какого-либо свойства
группы единиц или
совокупности в целом R
Слайд 2Статистический показатель
- количественно-качественная обобщающая характеристика какого-либо свойства
группы единиц или
совокупности в
целом
R
Слайд 3Типы показателей
Первичные (объемные, экстенсивные)
Вторичные (производные, интенсивные)
Индивидуальные (единичные)
Сводные (групповые, суммарные)
R
Слайд 4Абсолютные показатели
характеризуют абсолютные размеры явлений (масса, площадь, объем, количество)
Имеют размерность (ед.изм.)
натуральные
(куб.м., КВт ч, тонна, км,…)
условно-натуральные (усл.топливо, эталонный трактор,…)
стоимостные (денежные, сопоставимые)
трудовые (чел-день, чел-час) затраты труда, трудоемкость
условно-натуральные (усл.топливо, эталонный трактор,…)
стоимостные (денежные, сопоставимые)
трудовые (чел-день, чел-час) затраты труда, трудоемкость
Слайд 6Относительные показатели
- результат деления
двух абсолютных показателей =
текущий (сравниваемый)
база сравнения
Цели:
сравнение двух абсолютных
сравнение нескольких абсолютных с одним базовым
«цепное» сравнение ряда показателей
Цели:
сравнение двух абсолютных
сравнение нескольких абсолютных с одним базовым
«цепное» сравнение ряда показателей
Слайд 7Относительные показатели
- сравнение двух одноименных абсолютных показателей =
текущий
(сравниваемый) * масштаб
база сравнения
Виды: Масштаб базы: Размерность:
коэффициент (1) раз
процент (100 %) %
промилле (1000 %о) %о
продецимилле (10000 %оо) «на 10000…»
Виды: Масштаб базы: Размерность:
коэффициент (1) раз
процент (100 %) %
промилле (1000 %о) %о
продецимилле (10000 %оо) «на 10000…»
Слайд 8Относительные показатели
- сравнение двух разноименных абсолютных показателей =
текущий (сравниваемый)
база сравнения
Сочетание наименований
Затраты на хранение товара [% от цены / год]
Сочетание наименований
Затраты на хранение товара [% от цены / год]
Слайд 9Относительные показатели
Виды относительных показателей
Динамики (ОПД)
Плана (ОПП)
Выполнения плана (ОПВП)
Структуры (ОПСт)
Координации (ОПК)
Интенсивности и
уровня развития
Сравнения (ОПСр)
Сравнения (ОПСр)
Слайд 10ОП динамики
Для ряда динамики X1 … XN
ОПД = (тек.ур.) / (предыд.или
баз.ур.)
постоянная база (базисные ОПД)
сравнение с началом периода ОПД( i ) = Xi / X1 , i = 1..N, ОПД(1) = 1
переменная база (цепные ОПД)
сравнение с предыдущим периодом (темп роста) ОПД( i ) = Xi / Xi-1 , i = 2..N
постоянная база (базисные ОПД)
сравнение с началом периода ОПД( i ) = Xi / X1 , i = 1..N, ОПД(1) = 1
переменная база (цепные ОПД)
сравнение с предыдущим периодом (темп роста) ОПД( i ) = Xi / Xi-1 , i = 2..N
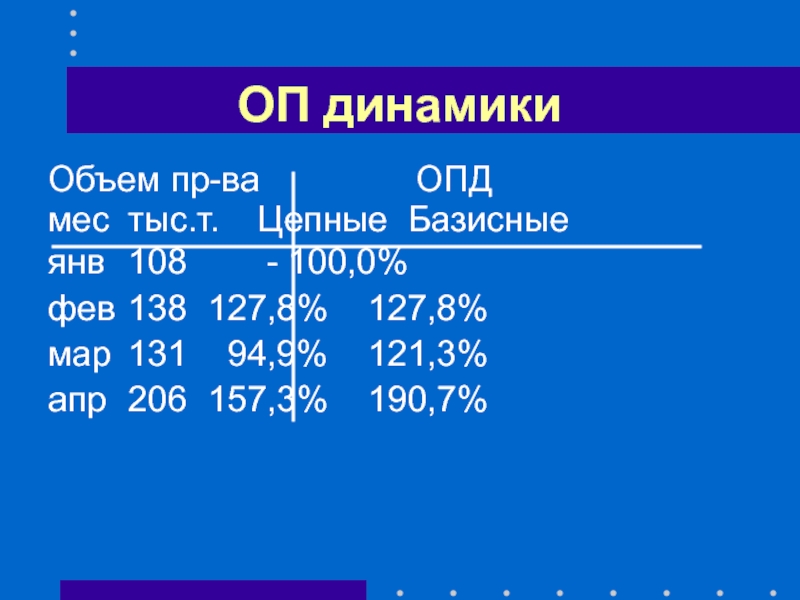
Слайд 11ОП динамики
Объем пр-ва ОПД
мес тыс.т. Цепные
Базисные
янв 108 - 100,0%
фев 138 127,8% 127,8%
мар 131 94,9% 121,3%
апр 206 157,3% 190,7%
янв 108 - 100,0%
фев 138 127,8% 127,8%
мар 131 94,9% 121,3%
апр 206 157,3% 190,7%
Слайд 12ОП плана и его выполнения
Для ряда плана Y1 … YN
ОППY( i
) = Yi+1 / Yi
(предстоит на следующий период)
Для ряда выполнения плана X1 … XN
ОПВПXY( i ) = Xi / Yi
(предстоит на следующий период)
Для ряда выполнения плана X1 … XN
ОПВПXY( i ) = Xi / Yi
Слайд 13ОП структуры и координации
Для набора показателей Y1 … YN
Структура:
ОПC( i )
= Yi / (Σ Yi )
Координация:
ОПК( i ) = Yi / Y1
Y1 - база сравнения:
- max(Yi )
- наибольший интерес
Координация:
ОПК( i ) = Yi / Y1
Y1 - база сравнения:
- max(Yi )
- наибольший интерес
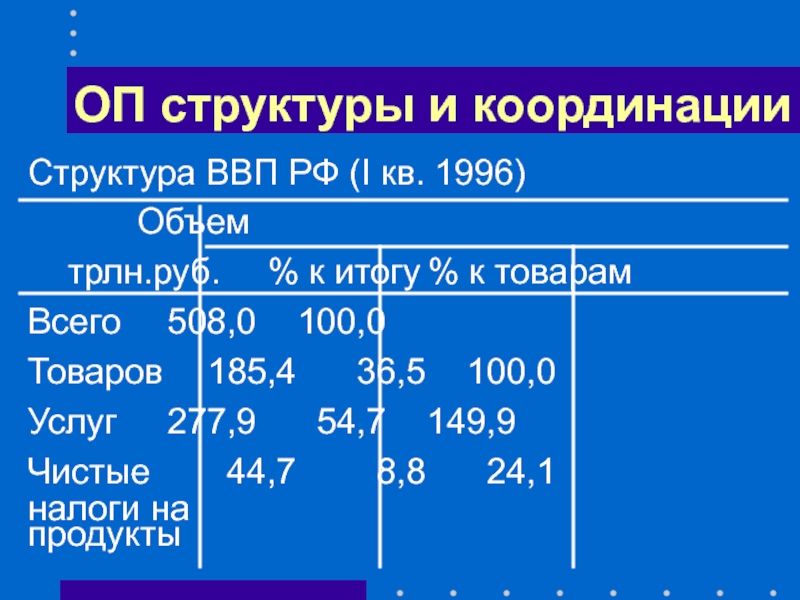
Слайд 14ОП структуры и координации
Структура ВВП РФ (I кв. 1996)
Объем
трлн.руб.
% к итогу % к товарам
Всего 508,0 100,0
Товаров 185,4 36,5 100,0
Услуг 277,9 54,7 149,9
Чистые 44,7 8,8 24,1
налоги на продукты
Всего 508,0 100,0
Товаров 185,4 36,5 100,0
Услуг 277,9 54,7 149,9
Чистые 44,7 8,8 24,1
налоги на продукты
Слайд 15ОП интенсивности
ОПИ = (характеристика явления А)
(распространенность А)
характеризует распространенность
явления (%, промилле, продецимилле)
Уровень обеспеченности автомобилями [число машин на 100 семей]
Плотность населения [число людей, приходящееся на 1 кв.км.]
Уровень предложения на рынке труда [число безработных на 1 вакансию]
Уровень обеспеченности автомобилями [число машин на 100 семей]
Плотность населения [число людей, приходящееся на 1 кв.км.]
Уровень предложения на рынке труда [число безработных на 1 вакансию]
Слайд 16ОП сравнения
Отношение одноименных абсолютных показателей, характеризующих разные объекты
ОПCр = (характеристика объекта
А)
(характеристика объекта B)
В Москве дилеров в 12,1 раза больше, чем в Новосибирске
Объем продаж обуви в 7 раз больше продаж одежды
(характеристика объекта B)
В Москве дилеров в 12,1 раза больше, чем в Новосибирске
Объем продаж обуви в 7 раз больше продаж одежды
Слайд 18Средняя величина
- обобщенный показатель, характеризующий типический уровень признака (средняя по типу)
Сравнение зарплат
на 2-х предприятиях:
по зарплатам 2-х работников (индив.)
по фонду оплаты труда (объемн.)
по средней зарплате (средн.)
по зарплатам 2-х работников (индив.)
по фонду оплаты труда (объемн.)
по средней зарплате (средн.)
Слайд 19Принципы применения
Для погашения индив. различий
Расчет по однородной совокупности
Подкрепление общих средних
групповыми средними
Учет
качественного содержания, взаимосвязи с другими признаками, имеющимися данными
Слайд 20Виды средних величин
Структурные
Степенные
Гармоническая m = -1
Геометрическая m →0
Арифметическая m = 1
Квадратичная m = 2
Кубическая m =
3
Мажорируемость: Xгарм≤Xгеом≤Xар≤Xкв≤Xкуб
Мажорируемость: Xгарм≤Xгеом≤Xар≤Xкв≤Xкуб
Слайд 23Виды степенных средних
Пример. Имеются данные о заработной плате десяти работников предприятия:
Вычислить
среднюю месячную зарплату рабочих:
Слайд 24Виды степенных средних
Пример. Имеются данные о стаже рабочих на предприятии:
Определить средний
стаж рабочих.
Слайд 25Пример 1 (выбор типа средней)
Какова средняя урожайность?
Культура Вал.сбор Посев.
(ц) площ. (га)
Пшеница 32 500 1 540
Рожь 1
620 120
Ячмень 13 640 460
Просо 1 650 80
Итого 49 410 2 200
Ячмень 13 640 460
Просо 1 650 80
Итого 49 410 2 200
У = Σ ВСi
Σ ППi
Слайд 26Пример 2 (выбор типа средней)
Какова средняя урожайность?
Культура Посев. Урожайность
площ. (га) (ц/га)
Пшеница 1 540 20
Рожь
120 19
Ячмень 460 28
Просо 80 13
Итого 2 200 ?
Ячмень 460 28
Просо 80 13
Итого 2 200 ?
У = Σ Уi ППi
Σ ППi
Слайд 27Пример 3 (выбор типа средней)
Какова средняя урожайность?
Культура Вал.сбор Урожайность
(ц) (ц/га)
Пшеница 32 500 25
Рожь 1 620 18
Ячмень 13 640 22
Просо
1 650 15
Итого 49 410 ?
Итого 49 410 ?
У = Σ ВСi__
Σ ВСi/Уi
Слайд 28Геометрическая средняя и ОПД
Объем пр-ва
ОПД
мес тыс.т. Цепные Базисные
янв 108 - 100,0% 0
фев 138 127,8% 127,8% 1
мар 131 94,9% 121,3% 2
апр 206 157,3% 190,7% 3
мес тыс.т. Цепные Базисные
янв 108 - 100,0% 0
фев 138 127,8% 127,8% 1
мар 131 94,9% 121,3% 2
апр 206 157,3% 190,7% 3
Слайд 29Структурные средние
Мода (наиболее частое значение)
Медиана (серединный объем)
Причины применения
Выявление внутреннего строения ряда
распределения признака
При невозможности определения среднего в интервальном ряде распределения
При невозможности определения среднего в интервальном ряде распределения
Слайд 30Пример: структурные средние
Группы Себе- Число Объем Затраты
пред- стоимость пред- прод. на пр-во
приятий (т.руб.) прият. (%) (млн.р.)
1 110-115 8 9 16,4
2 115-120
16 18 34,4
3 120-125 24 24 47,8
4 125 и выше 52 49 101,4
Итого - 100 100 200,0
3 120-125 24 24 47,8
4 125 и выше 52 49 101,4
Итого - 100 100 200,0
Слайд 31Расчет моды
Мо = ХМо + hМо
[fMo-fMo-1] / [(fMo-fMo-1)+(fMo-fMo+1)]
ХМо - нижняя
гр. модального инт.
hМo - ширина модального инт.
fМо - объем в медианном интервале
f Мо-1 - объем в предыдущем инт.
f Мо+1 - объем в следующем инт.
hМo - ширина модального инт.
fМо - объем в медианном интервале
f Мо-1 - объем в предыдущем инт.
f Мо+1 - объем в следующем инт.
Слайд 33Расчет медианы
Ме = ХМе + hМе [(n/2)-SМе-1]/ fМе
ХМе - нижняя гр. медианного
инт.
hМе - ширина медианного инт.
n/2 - половина объема взвеш. показ.
SМе-1 - накопленный до мед.инт. объем
fМе - объем в медианном интервале
hМе - ширина медианного инт.
n/2 - половина объема взвеш. показ.
SМе-1 - накопленный до мед.инт. объем
fМе - объем в медианном интервале
Слайд 43Вариация
- различие в значениях показателя у разных единиц совокупности в один и
тот же период или момент времени
Показатель вариации характеризует:
Структуру явления (степень отклонения варианты от средней)
Точность определения средней величины
Показатель вариации характеризует:
Структуру явления (степень отклонения варианты от средней)
Точность определения средней величины
Слайд 44Показатели вариации
Размах вариации
Среднее линейное отклонение
Дисперсия
Среднее квадратическое отклонение
Коэффициент вариации
Слайд 45Размах вариации
R = Xmax - Xmin
Характеристика возможных резервов (в предположении, что
часть единиц может достичь наилучшего показателя)
Слайд 46Среднее линейное отклонение
Для несгруппированных данных
d = (1/N)Σi=1..N | Xi - X
|
Для вариационного ряда (сгруппир.)
d = Σi=1..m | Xi - X | fi / Σi=1..m fi
Для вариационного ряда (сгруппир.)
d = Σi=1..m | Xi - X | fi / Σi=1..m fi
Слайд 47Дисперсия
Простая дисперсия
для несгруппированных данных
σ 2 = (1/N)Σi=1..N | Xi -
X |2
Взвешенная дисперсия для вариационного ряда
σ 2 = Σi=1..m | Xi - X |2 fi / Σi=1..m fi
Взвешенная дисперсия для вариационного ряда
σ 2 = Σi=1..m | Xi - X |2 fi / Σi=1..m fi
Слайд 52Среднее квадратическое откл.
σ = (σ 2)1/2
Преимущества:
Измеряется в единицах варианты
В предположении нормальности
варианты применимо правило k сигм
⇒ Удобно давать экономическую интерпретацию
⇒ Удобно давать экономическую интерпретацию
Слайд 53Коэффициент вариации
V = (σ / X) 100%
Только для положительных вариант
Позволяет сравнивать
степень колеблемости показателей
Совокупность считается количественно однородной, если V<33%
Совокупность считается количественно однородной, если V<33%
~
