- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рыночные взаимодействия в условиях несовершенной конкуренции. (Тема 4) презентация
Содержание
- 1. Рыночные взаимодействия в условиях несовершенной конкуренции. (Тема 4)
- 2. Рыночные взаимодействия в условиях несовершенной конкуренции Монопольная
- 3. 1.Монопольная власть
- 4. 1.Монопольная власть Пусть доход R фирмы-монополиста
- 5. 1.Монопольная власть
- 6. 1.Монопольная власть Источники монопольной
- 7. 1.Монопольная власть
- 8. 2.1.Модель дуополии Курно C1 = cy1 +
- 9. 2.1.Модель дуополии Курно p = a −
- 10. 2.1.Модель дуополии Курно
- 11. 2.1.Модель дуополии Курно
- 12. 2.1.Модель дуополии Курно
- 13. 2.1.Модель дуополии Курно
- 14. 2.1.Модель дуополии Курно
- 15. 2.2.Модель олигополии Курно
- 16. 2.2.Модель олигополии Курно
- 17. 2.2.Модель олигополии Курно
- 18. 2.2.Модель олигополии Курно
- 19. 2.2.Модель олигополии Курно
- 20. 2.2.Модель олигополии Курно
- 21. 3.1.Модель дуополии Штакельберга
- 22. 3.1.Модель дуополии Штакельберга
- 23. 3.1.Модель дуополии Штакельберга
- 24. 3.1.Модель дуополии Штакельберга
- 25. 3.1.Модель дуополии Штакельберга
- 26. 3.1.Модель дуополии Штакельберга
- 27. 3.1.Модель дуополии Штакельберга
- 28. 3.2.Модель олигополии Штакельберга Предпосылки: На рынке функционируют
- 29. 3.2.Модель олигополии Штакельберга
- 30. 3.2.Модель олигополии Штакельберга
- 31. 3.2.Модель олигополии Штакельберга
- 32. 3.2.Модель олигополии Штакельберга
- 33. 4.Модель сговора в дуополии и олигополии В
- 34. 4.Модель сговора в дуополии и олигополии Пусть
- 35. 4.Модель сговора в дуополии и олигополии
- 36. 4.Модель сговора в дуополии и олигополии
- 37. 4.Модель дуополии и олигополии Бертрана Модель дуополии
- 38. 4.Модель дуополии и олигополии Бертрана Модель дуополии
- 39. 4.Модель дуополии и олигополии Бертрана
- 40. 4.Модель дуополии и олигополии Бертрана
Рыночные взаимодействия в условиях несовершенной конкуренции Монопольная власть Модели дуополии и олигополии Курно. Модели дуополии и олигополии Штакельберга. Модели сговора в дуополии и олигополии. Модели дуополии и олигополии Бертрана.
Слайд 2Рыночные взаимодействия в условиях несовершенной конкуренции
Монопольная власть
Модели дуополии и олигополии Курно.
Модели
дуополии и олигополии Штакельберга.
Модели сговора в дуополии и олигополии.
Модели дуополии и олигополии Бертрана.
Модели сговора в дуополии и олигополии.
Модели дуополии и олигополии Бертрана.
Слайд 41.Монопольная власть
Пусть доход R фирмы-монополиста R(y) = p(y)*y.
p(y) – цена
товара
y –объем производства товара
y –объем производства товара
Слайд 61.Монопольная власть
Источники монопольной власти:
Эластичность спроса;
Концентрация фирм на рынке;
Взаимосвязь фирм на рынке.
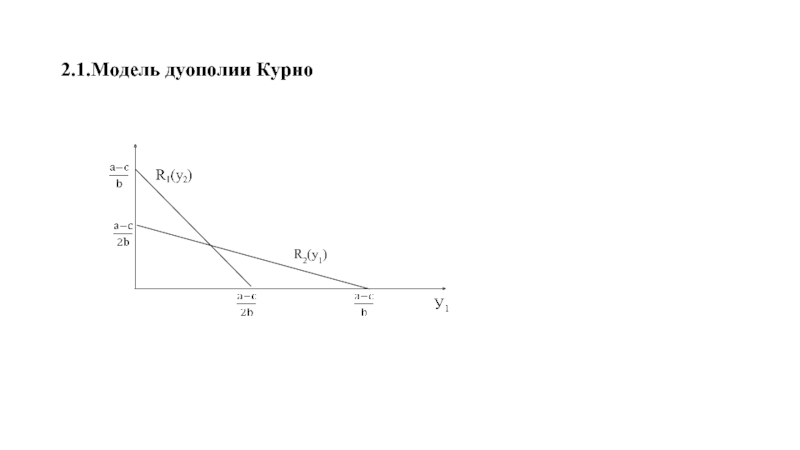
Слайд 82.1.Модель дуополии Курно
C1 = cy1 + d1, C2 = cy2
+ d2, где
c = MC1 = MC2, d1 = FC1, d2 = FC2;
y1 – объем выпуска первой фирмы;
y2 – объем выпуска второй фирмы;
y = y1 + y2 – суммарный выпуск обеих фирм (т.е. отраслевой выпуск);
MC1 и MC2 – предельные издержки фирм;
FC1 и FC2 – постоянные издержки обеих фирм.
c = MC1 = MC2, d1 = FC1, d2 = FC2;
y1 – объем выпуска первой фирмы;
y2 – объем выпуска второй фирмы;
y = y1 + y2 – суммарный выпуск обеих фирм (т.е. отраслевой выпуск);
MC1 и MC2 – предельные издержки фирм;
FC1 и FC2 – постоянные издержки обеих фирм.
Слайд 92.1.Модель дуополии Курно
p = a − b(y1 + y2),
где a и
b – положительные параметры.
R1 = py1
R2 = py2.
R1 = py1
R2 = py2.
Слайд 283.2.Модель олигополии Штакельберга
Предпосылки:
На рынке функционируют n фирм.
Функция издержек фирмы-лидера С1 =
с1у1+d1
Предельные издержки фирм-последователей одинаковы и строго больше предельных издержек фирмы-лидера.
Каждая фирма-последователь полагает, что выпуск фирмы-лидера и других фирм-последователей в данном производственном периоде фиксирован.
Функция, обратная к функции рыночного спроса, имеет вид:
p = a − by = a − b(y1 + … + yn), где a и b – положительные параметры.
Предельные издержки фирм-последователей одинаковы и строго больше предельных издержек фирмы-лидера.
Каждая фирма-последователь полагает, что выпуск фирмы-лидера и других фирм-последователей в данном производственном периоде фиксирован.
Функция, обратная к функции рыночного спроса, имеет вид:
p = a − by = a − b(y1 + … + yn), где a и b – положительные параметры.
Слайд 334.Модель сговора в дуополии и олигополии
В модели сговора (модели картеля) фирмы
объединяются для принятия решения относительно рыночной цены и общего объема выпуска.
В этой модели все фирмы на рынке выступают как одна фирма-монополист.
В этой модели все фирмы на рынке выступают как одна фирма-монополист.
Слайд 344.Модель сговора в дуополии и олигополии
Пусть на рынке в течение производственного
периода функционируют две фирмы.
Их функции издержек являются линейными функциями, т.е. имеют вид C1 = cy1 + d1, C2 = cy2 + d2
Функция, обратная к функции рыночного спроса, предполагается линейной и имеет вид p = a − by
Общая прибыль двух фирм:
PR(y) = py − C1 − C2 = (a − by)y − cy1 − d1 − cy2 − d2,
Или PR = (a − c− by)y – d1− d2
Их функции издержек являются линейными функциями, т.е. имеют вид C1 = cy1 + d1, C2 = cy2 + d2
Функция, обратная к функции рыночного спроса, предполагается линейной и имеет вид p = a − by
Общая прибыль двух фирм:
PR(y) = py − C1 − C2 = (a − by)y − cy1 − d1 − cy2 − d2,
Или PR = (a − c− by)y – d1− d2
Слайд 374.Модель дуополии и олигополии Бертрана
Модель дуополии Бертрана представляет собой модель ценовой
дуополии. Для фирмы постоянным является не объем выпуска фирмы-конкурента, а назначаемая конкурентом цена.
Модель дуополии с однородным продуктом
Предпосылка:
Предельные издержки фирм одинаковы.
В этих условиях потребители покупают товары той фирмы, которая предлагает меньшую цену.
Эта модель равнозначна модели совершенной конкуренции, и равновесие Бертрана достигается, когда цена каждой фирмы равна предельным издержкам.
Таким образом, дуополия Бертрана с однородным продуктом функционирует как рынок совершенной конкуренции (парадокс Бертрана).
Модель дуополии с однородным продуктом
Предпосылка:
Предельные издержки фирм одинаковы.
В этих условиях потребители покупают товары той фирмы, которая предлагает меньшую цену.
Эта модель равнозначна модели совершенной конкуренции, и равновесие Бертрана достигается, когда цена каждой фирмы равна предельным издержкам.
Таким образом, дуополия Бертрана с однородным продуктом функционирует как рынок совершенной конкуренции (парадокс Бертрана).
Слайд 384.Модель дуополии и олигополии Бертрана
Модель дуополии с дифференцированным продуктом.
Пусть функции
спроса на продукцию каждой фирмы имеют одни и те же параметры и выглядят так:
y1 = h − gp1 + kp2, y2 = h − gp2 + kp1.
Все параметры h, g, k – положительные постоянные.
PR1 = p1y1 − cy1 − d1 = (p1 − c)(h − gp1 + kp2) − d1
y1 = h − gp1 + kp2, y2 = h − gp2 + kp1.
Все параметры h, g, k – положительные постоянные.
PR1 = p1y1 − cy1 − d1 = (p1 − c)(h − gp1 + kp2) − d1
