Combinations of Options
22.7 Valuing Options
22.8 An Option‑Pricing Formula
22.9 Stocks and Bonds as Options
22.10 Capital-Structure Policy and Options
22.11 Mergers and Options
22.12 Investment in Real Projects and Options
22.13 Summary and Conclusions
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Options презентация
Содержание
- 1. Options
- 2. 22.1 Options Many corporate securities are similar
- 3. 22.1 Options Contracts: Preliminaries An option gives
- 4. 22.1 Options Contracts: Preliminaries Exercising the Option
- 5. Options Contracts: Preliminaries In-the-Money The exercise price
- 6. Options Contracts: Preliminaries Intrinsic Value The difference
- 7. 22.2 Call Options Call options gives the
- 8. Basic Call Option Pricing Relationships at Expiry
- 9. Call Option Payoffs -20 100 90 80
- 10. Call Option Payoffs Write a call Exercise price = $50
- 11. Call Option Profits Write a call Buy
- 12. 22.3 Put Options Put options give the
- 13. Basic Put Option Pricing Relationships at Expiry
- 14. Put Option Payoffs -20 100 90 80
- 15. Put Option Payoffs -20 100 90 80
- 16. Put Option Profits -20 100 90 80
- 17. 22.4 Selling Options The seller (or writer)
- 18. 22.5 Stock Option Quotations
- 19. 22.5 Stock Option Quotations This option has
- 20. 22.5 Stock Option Quotations This makes a
- 21. 22.5 Stock Option Quotations On this
- 22. 22.5 Stock Option Quotations The holder of
- 23. 22.5 Stock Option Quotations Buying this CALL
- 24. 22.5 Stock Option Quotations On this
- 25. 22.6 Combinations of Options Puts and calls
- 26. Protective Put Strategy: Buy a Put
- 27. Protective Put Strategy Profits Buy a put
- 28. Covered Call Strategy Sell a call with
- 29. Long Straddle: Buy a Call and a
- 30. Short Straddle: Sell a Call and a
- 31. Long Call Spread Sell a call with
- 32. Put-Call Parity Sell a put with an
- 33. 22.7 Valuing Options The last section concerned
- 34. Option Value Determinants Call Put Stock
- 35. Market Value, Time Value,
- 36. 22.8 An Option‑Pricing Formula We will start
- 37. Binomial Option Pricing Model Suppose a
- 38. Binomial Option Pricing Model A call option
- 39. Binomial Option Pricing Model Borrow the present
- 40. Binomial Option Pricing Model The
- 41. Binomial Option Pricing Model We can value
- 42. The Binomial Option Pricing Model If the
- 43. The Binomial Option Pricing Model If the
- 44. Binomial Option Pricing Model the replicating portfolio
- 45. The Risk-Neutral Approach to Valuation We could
- 46. The Risk-Neutral Approach to Valuation S(0)
- 47. The Risk-Neutral Approach to Valuation The key
- 48. Example of the Risk-Neutral Valuation of a
- 49. Example of the Risk-Neutral Valuation of a
- 50. Example of the Risk-Neutral Valuation of a
- 51. Example of the Risk-Neutral Valuation of a
- 52. Risk-Neutral Valuation and the Replicating Portfolio This
- 53. The Black-Scholes Model The Black-Scholes Model is
- 54. The Black-Scholes Model Find the value of
- 55. The Black-Scholes Model Let’s try our hand
- 56. The Black-Scholes Model N(d1) = N(0.52815) = 0.7013 N(d2) = N(0.31602) = 0.62401
- 57. Assume S = $50, X = $45,
- 58. 22.9 Stocks and Bonds as Options Levered
- 59. 22.9 Stocks and Bonds as Options Levered
- 60. 22.9 Stocks and Bonds as Options It
- 61. 22.10 Capital-Structure Policy and Options Recall some
- 62. Balance Sheet for a Company in Distress
- 63. Selfish Strategy 1: Take Large Risks
- 64. Selfish Stockholders Accept Negative NPV Project
- 65. 22.11 Mergers and Options This is an
- 66. 22.12 Investment in Real Projects & Options
- 67. 22.13 Summary and Conclusions The most familiar
- 68. 22.13 Summary and Conclusions The value of
22.1 Options Many corporate securities are similar to the stock options that are traded on organized exchanges. Almost every issue of corporate stocks and bonds has option features. In addition,
Слайд 122.1 Options
22.2 Call Options
22.3 Put Options
22.4 Selling Options
22.5 Stock Option Quotations
22.6
Слайд 222.1 Options
Many corporate securities are similar to the stock options that
are traded on organized exchanges.
Almost every issue of corporate stocks and bonds has option features.
In addition, capital structure and capital budgeting decisions can be viewed in terms of options.
Almost every issue of corporate stocks and bonds has option features.
In addition, capital structure and capital budgeting decisions can be viewed in terms of options.
Слайд 322.1 Options Contracts: Preliminaries
An option gives the holder the right, but
not the obligation, to buy or sell a given quantity of an asset on (or perhaps before) a given date, at prices agreed upon today.
Calls versus Puts
Call options gives the holder the right, but not the obligation, to buy a given quantity of some asset at some time in the future, at prices agreed upon today. When exercising a call option, you “call in” the asset.
Put options gives the holder the right, but not the obligation, to sell a given quantity of an asset at some time in the future, at prices agreed upon today. When exercising a put, you “put” the asset to someone.
Calls versus Puts
Call options gives the holder the right, but not the obligation, to buy a given quantity of some asset at some time in the future, at prices agreed upon today. When exercising a call option, you “call in” the asset.
Put options gives the holder the right, but not the obligation, to sell a given quantity of an asset at some time in the future, at prices agreed upon today. When exercising a put, you “put” the asset to someone.
Слайд 422.1 Options Contracts: Preliminaries
Exercising the Option
The act of buying or selling
the underlying asset through the option contract.
Strike Price or Exercise Price
Refers to the fixed price in the option contract at which the holder can buy or sell the underlying asset.
Expiry
The maturity date of the option is referred to as the expiration date, or the expiry.
European versus American options
European options can be exercised only at expiry.
American options can be exercised at any time up to expiry.
Strike Price or Exercise Price
Refers to the fixed price in the option contract at which the holder can buy or sell the underlying asset.
Expiry
The maturity date of the option is referred to as the expiration date, or the expiry.
European versus American options
European options can be exercised only at expiry.
American options can be exercised at any time up to expiry.
Слайд 5Options Contracts: Preliminaries
In-the-Money
The exercise price is less than the spot price
of the underlying asset.
At-the-Money
The exercise price is equal to the spot price of the underlying asset.
Out-of-the-Money
The exercise price is more than the spot price of the underlying asset.
At-the-Money
The exercise price is equal to the spot price of the underlying asset.
Out-of-the-Money
The exercise price is more than the spot price of the underlying asset.
Слайд 6Options Contracts: Preliminaries
Intrinsic Value
The difference between the exercise price of the
option and the spot price of the underlying asset.
Speculative Value
The difference between the option premium and the intrinsic value of the option.
Speculative Value
The difference between the option premium and the intrinsic value of the option.
Option Premium
=
Intrinsic Value
Speculative Value
+
Слайд 722.2 Call Options
Call options gives the holder the right, but not
the obligation, to buy a given quantity of some asset on or before some time in the future, at prices agreed upon today.
When exercising a call option, you “call in” the asset.
When exercising a call option, you “call in” the asset.
Слайд 8Basic Call Option Pricing Relationships at Expiry
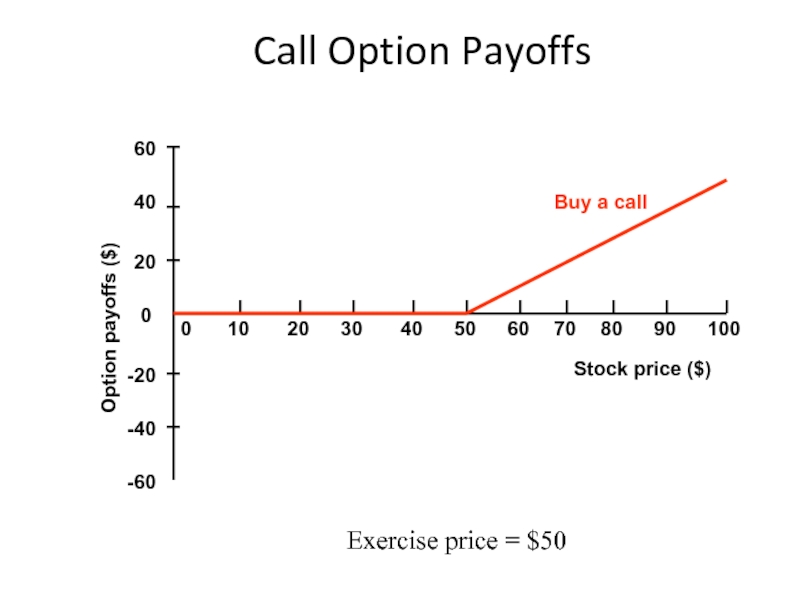
At expiry, an American call
option is worth the same as a European option with the same characteristics.
If the call is in-the-money, it is worth ST - E.
If the call is out-of-the-money, it is worthless.
CaT = CeT = Max[ST - E, 0]
Where
ST is the value of the stock at expiry (time T)
E is the exercise price.
CaT is the value of an American call at expiry
CeT is the value of a European call at expiry
If the call is in-the-money, it is worth ST - E.
If the call is out-of-the-money, it is worthless.
CaT = CeT = Max[ST - E, 0]
Where
ST is the value of the stock at expiry (time T)
E is the exercise price.
CaT is the value of an American call at expiry
CeT is the value of a European call at expiry
Слайд 9Call Option Payoffs
-20
100
90
80
70
60
0
10
20
30
40
50
-40
20
0
-60
40
60
Stock price ($)
Option payoffs ($)
Buy a call
Exercise price =
$50
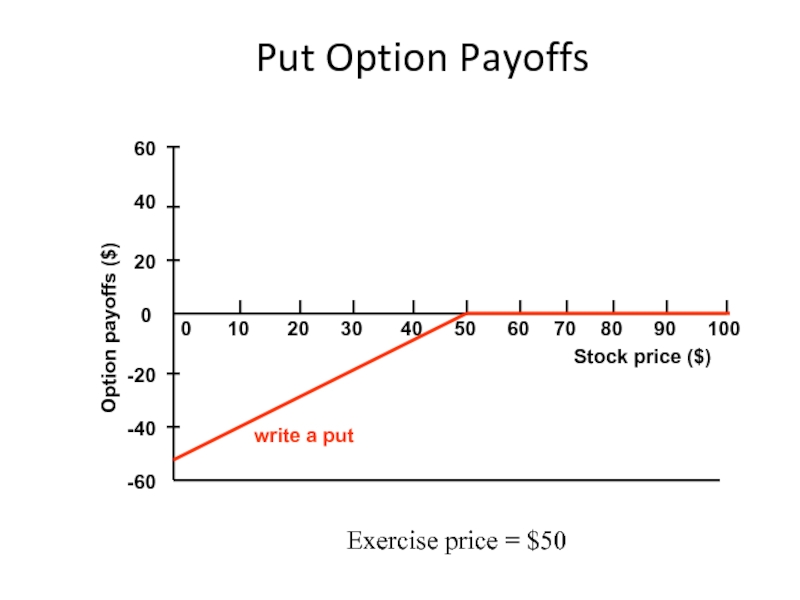
Слайд 1222.3 Put Options
Put options give the holder the right, but not
the obligation, to sell a given quantity of an asset on or before some time in the future, at prices agreed upon today.
When exercising a put, you “put” the asset to someone.
When exercising a put, you “put” the asset to someone.
Слайд 13Basic Put Option Pricing Relationships at Expiry
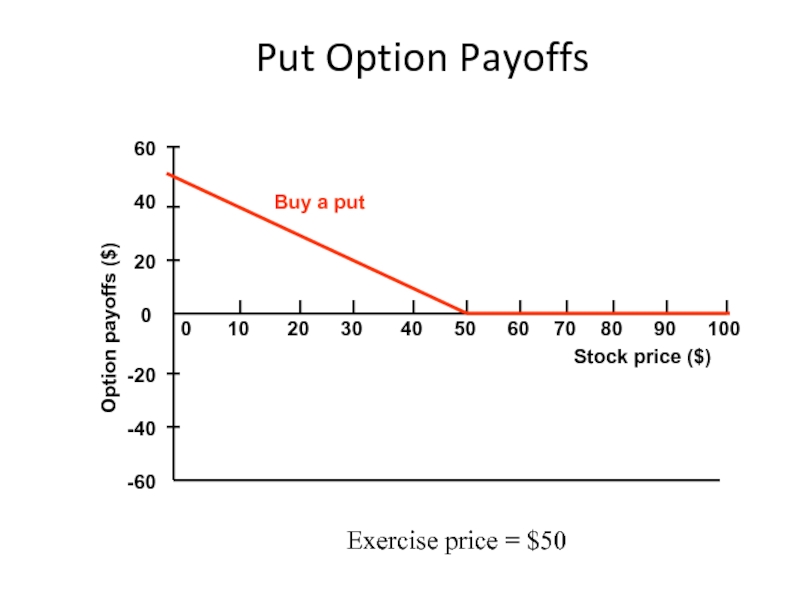
At expiry, an American put
option is worth the same as a European option with the same characteristics.
If the put is in-the-money, it is worth E - ST.
If the put is out-of-the-money, it is worthless.
PaT = PeT = Max[E - ST, 0]
If the put is in-the-money, it is worth E - ST.
If the put is out-of-the-money, it is worthless.
PaT = PeT = Max[E - ST, 0]
Слайд 14Put Option Payoffs
-20
100
90
80
70
60
0
10
20
30
40
50
-40
20
0
-60
40
60
Stock price ($)
Option payoffs ($)
Buy a put
Exercise price =
$50
Слайд 15Put Option Payoffs
-20
100
90
80
70
60
0
10
20
30
40
50
-40
20
0
-60
40
60
Option payoffs ($)
write a put
Exercise price = $50
Stock price
($)
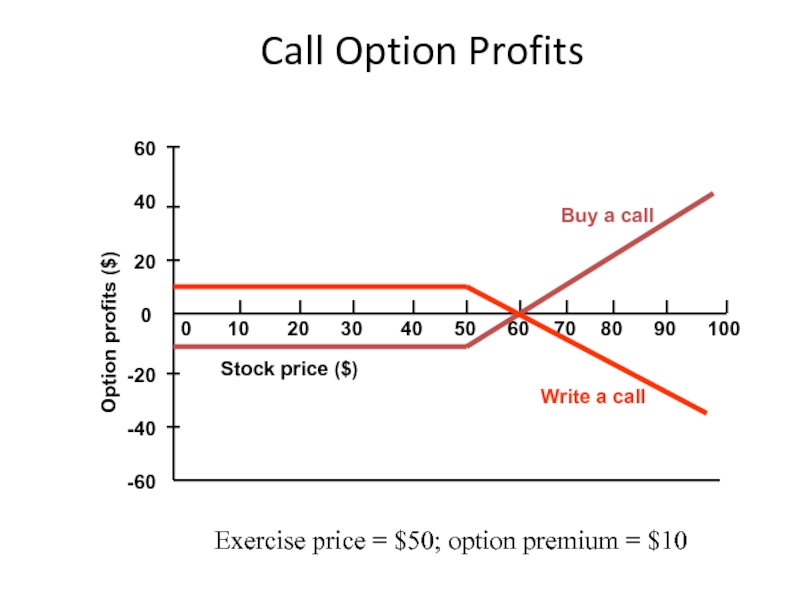
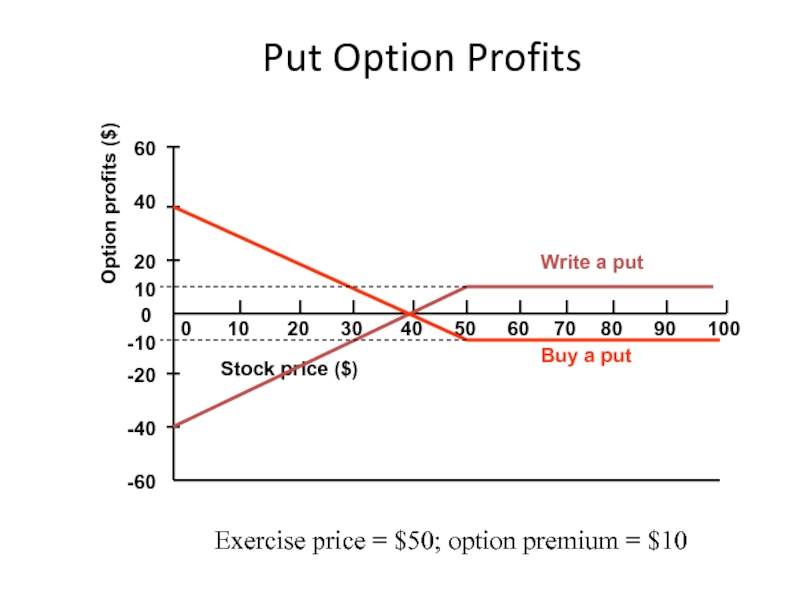
Слайд 16Put Option Profits
-20
100
90
80
70
60
0
10
20
30
40
50
-40
20
0
-60
40
60
Stock price ($)
Option profits ($)
Buy a put
Write a put
Exercise
price = $50; option premium = $10
10
-10
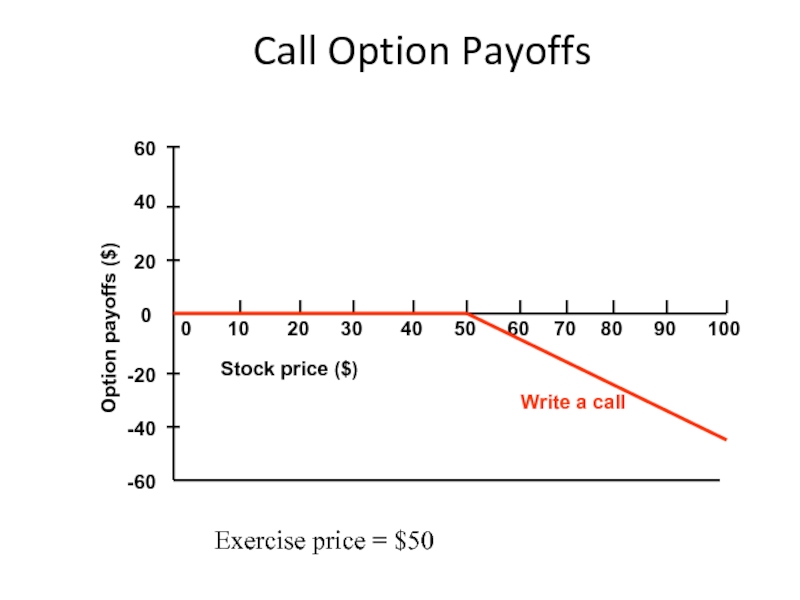
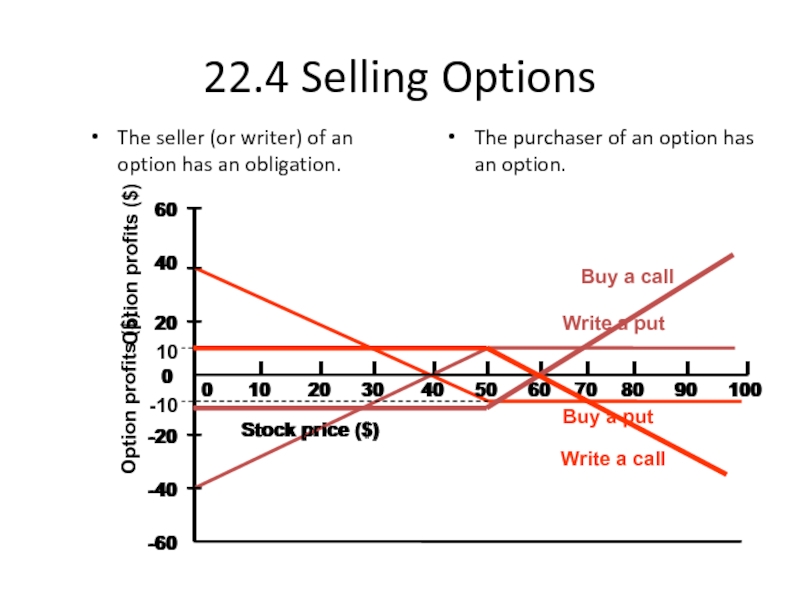
Слайд 1722.4 Selling Options
The seller (or writer) of an option has an
obligation.
The purchaser of an option has an option.
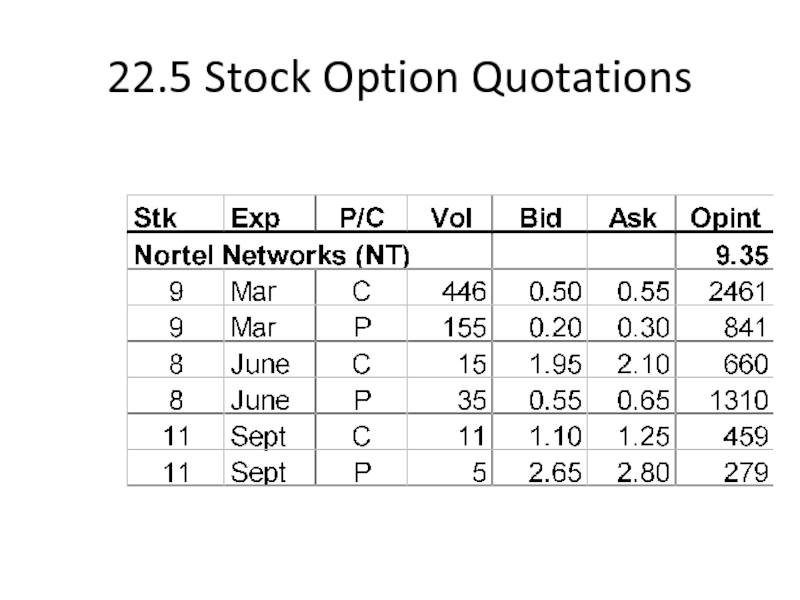
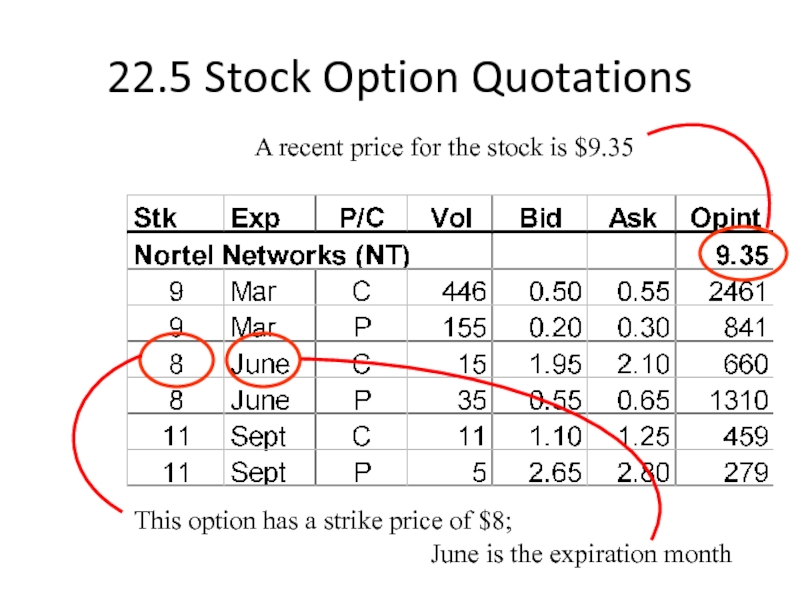
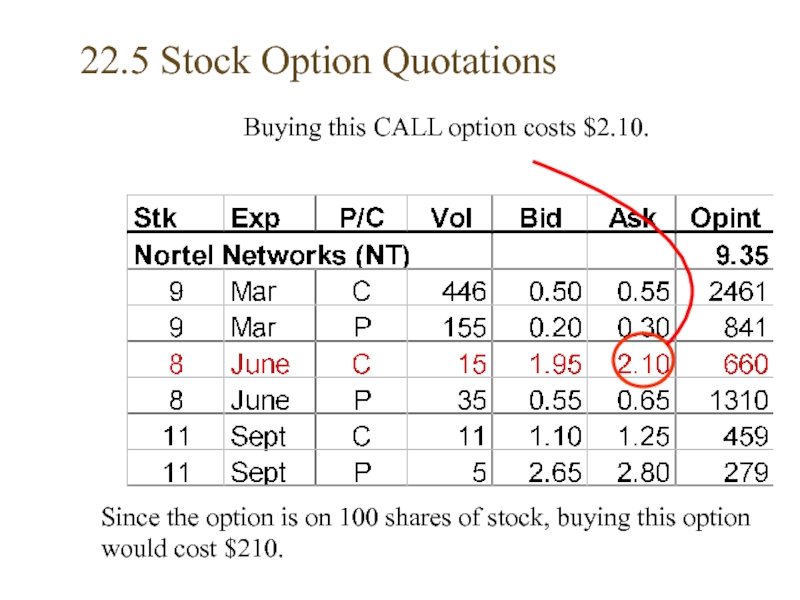
Слайд 1922.5 Stock Option Quotations
This option has a strike price of $8;
A
recent price for the stock is $9.35
June is the expiration month
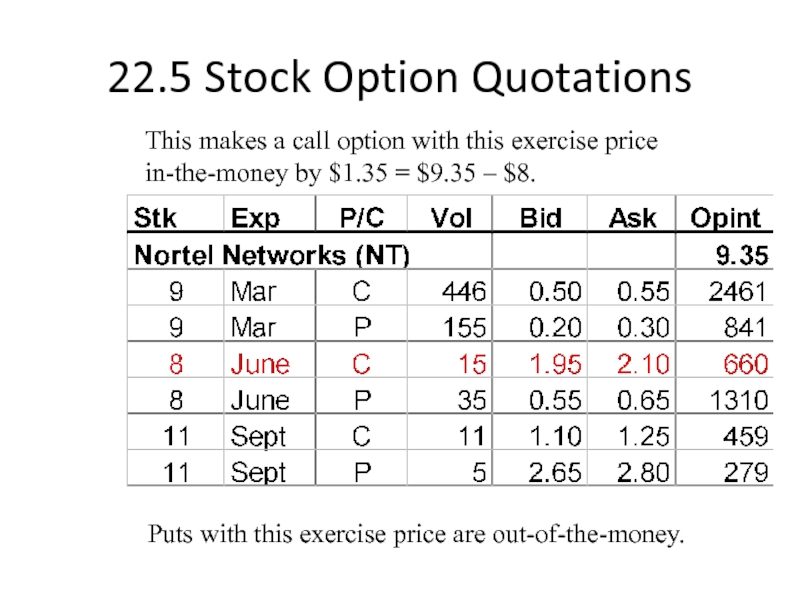
Слайд 2022.5 Stock Option Quotations
This makes a call option with this exercise
price in-the-money by $1.35 = $9.35 – $8.
Puts with this exercise price are out-of-the-money.
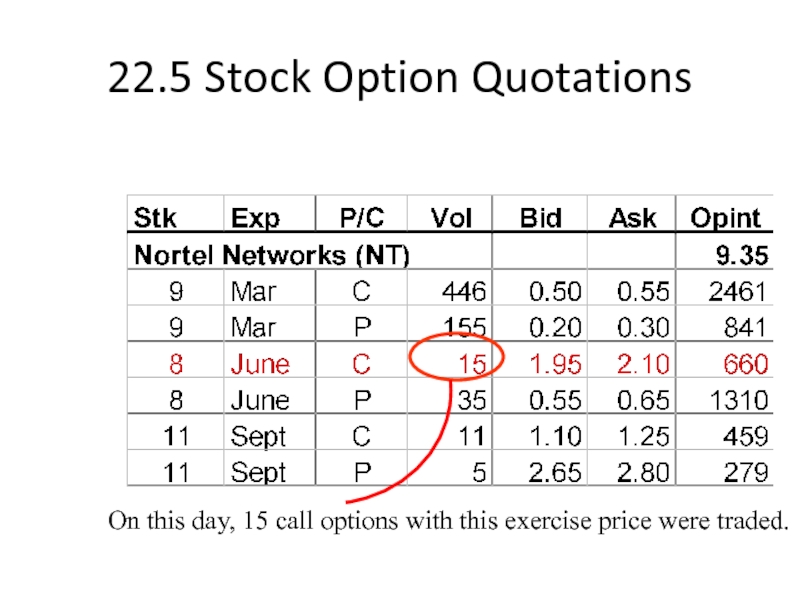
Слайд 2122.5 Stock Option Quotations
On this day, 15 call options with this
exercise price were traded.
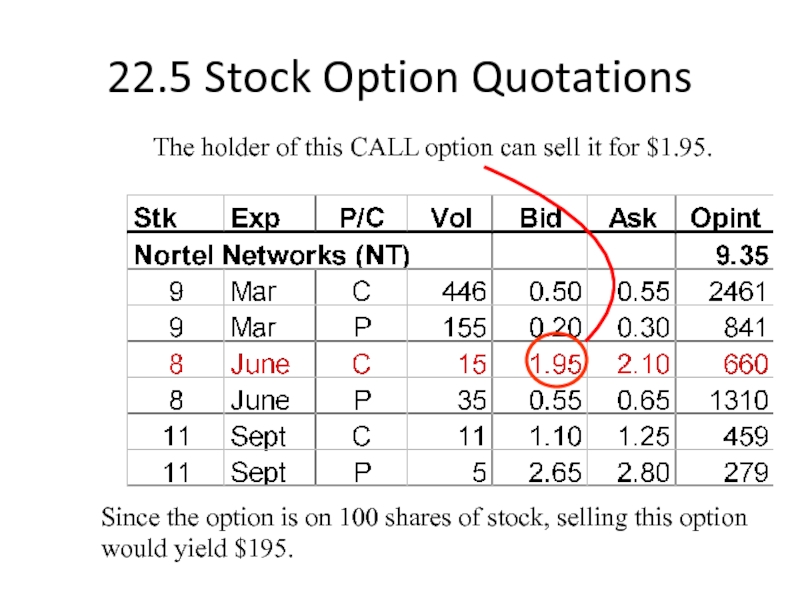
Слайд 2222.5 Stock Option Quotations
The holder of this CALL option can sell
it for $1.95.
Since the option is on 100 shares of stock, selling this option would yield $195.
Слайд 2322.5 Stock Option Quotations
Buying this CALL option costs $2.10.
Since the option
is on 100 shares of stock, buying this option would cost $210.
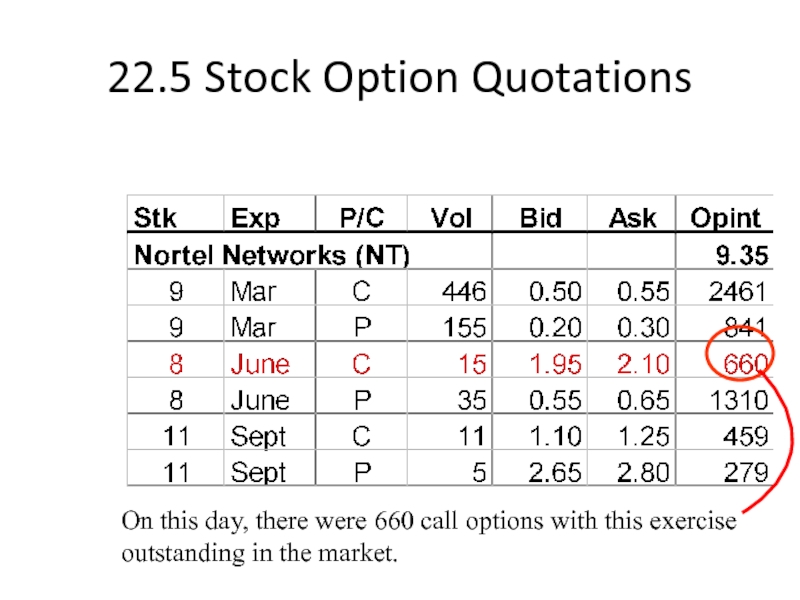
Слайд 2422.5 Stock Option Quotations
On this day, there were 660 call options
with this exercise outstanding in the market.
Слайд 2522.6 Combinations of Options
Puts and calls can serve as the building
blocks for more complex option contracts.
If you understand this, you can become a financial engineer, tailoring the risk-return profile to meet your client’s needs.
If you understand this, you can become a financial engineer, tailoring the risk-return profile to meet your client’s needs.
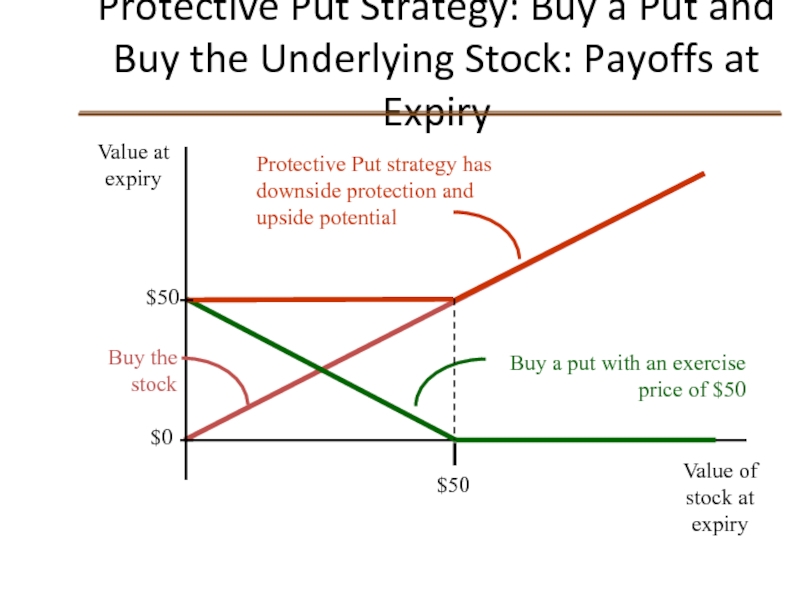
Слайд 26
Protective Put Strategy: Buy a Put and Buy the Underlying Stock:
Payoffs at Expiry
Buy a put with an exercise price of $50
Buy the stock
Protective Put strategy has downside protection and upside potential
$50
$0
$50
Value at expiry
Value of stock at expiry
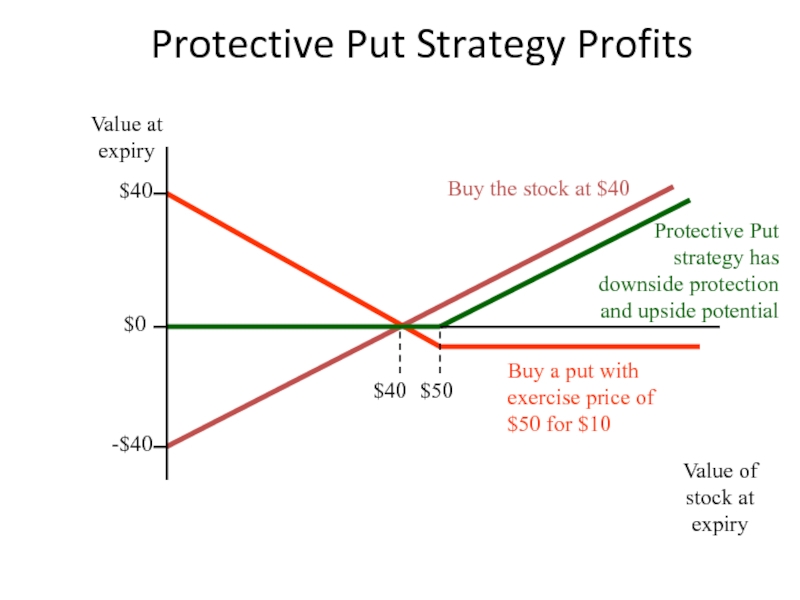
Слайд 27Protective Put Strategy Profits
Buy a put with exercise price of $50
for $10
Buy the stock at $40
$40
Protective Put strategy has downside protection and upside potential
$40
$0
-$40
$50
Value at expiry
Value of stock at expiry
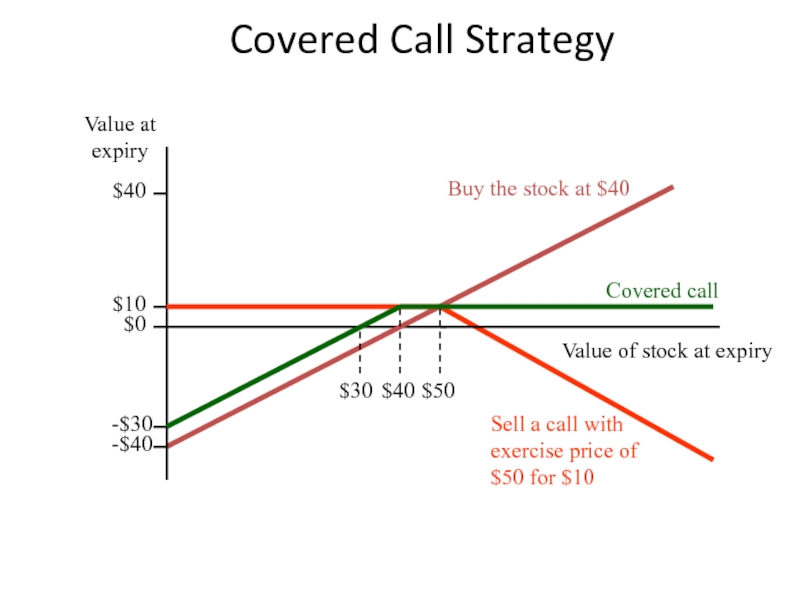
Слайд 28Covered Call Strategy
Sell a call with exercise price of $50 for
$10
Buy the stock at $40
$40
Covered call
$40
$0
-$40
$10
-$30
$30
$50
Value of stock at expiry
Value at expiry
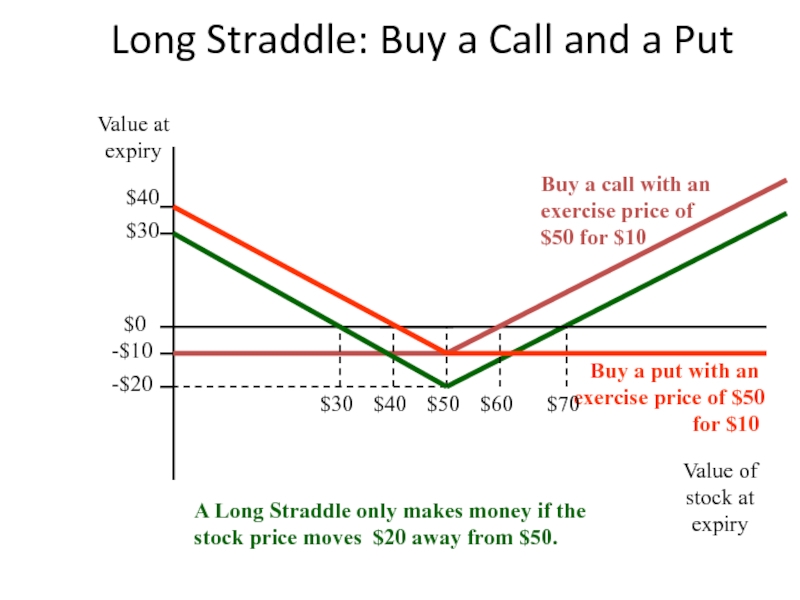
Слайд 29Long Straddle: Buy a Call and a Put
Buy a put with
an exercise price of $50 for $10
$40
A Long Straddle only makes money if the stock price moves $20 away from $50.
$40
$0
-$20
$50
Buy a call with an exercise price of $50 for $10
-$10
$30
$60
$30
$70
Value of stock at expiry
Value at expiry
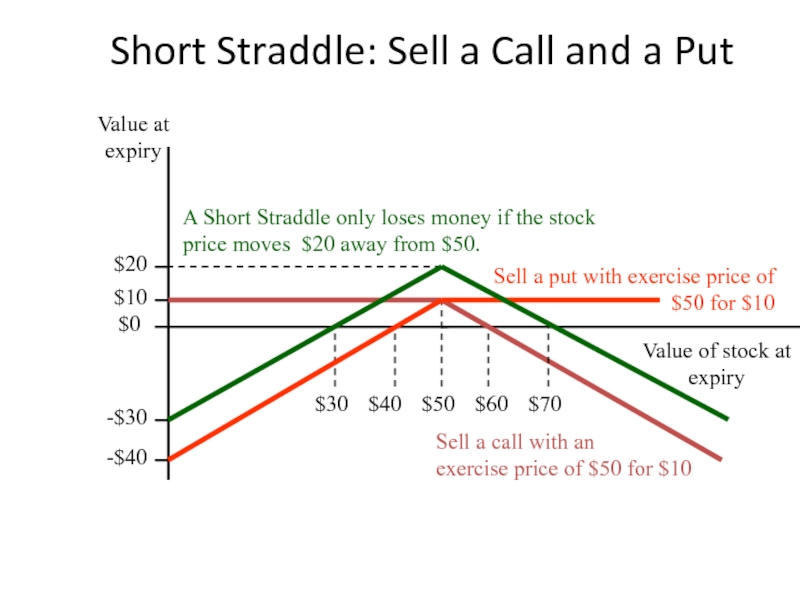
Слайд 30Short Straddle: Sell a Call and a Put
Sell a put with
exercise price of
$50 for $10
$50 for $10
$40
A Short Straddle only loses money if the stock price moves $20 away from $50.
-$40
$0
-$30
$50
Sell a call with an
exercise price of $50 for $10
$10
$20
$60
$30
$70
Value of stock at expiry
Value at expiry
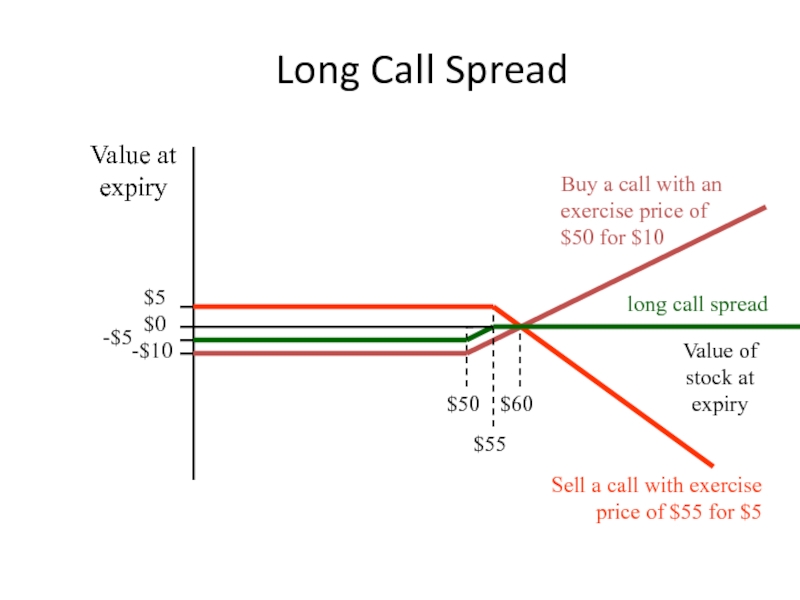
Слайд 31Long Call Spread
Sell a call with exercise price of $55 for
$5
$55
long call spread
$5
$0
$50
Buy a call with an exercise price of $50 for $10
-$10
-$5
$60
Value of stock at expiry
Value at expiry
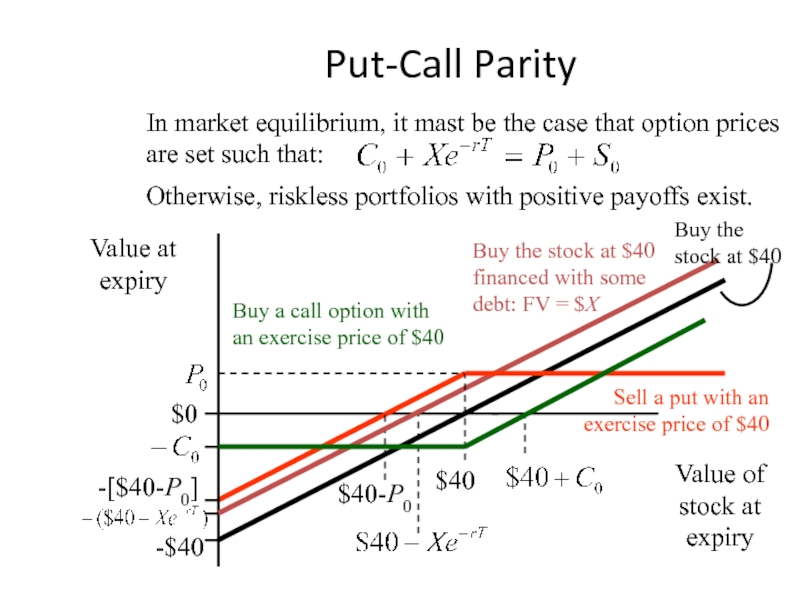
Слайд 32Put-Call Parity
Sell a put with an exercise price of $40
Buy the
stock at $40 financed with some debt: FV = $X
Buy a call option with an exercise price of $40
$0
-$40
$40-P0
$40
Buy the stock at $40
-[$40-P0]
In market equilibrium, it mast be the case that option prices are set such that:
Otherwise, riskless portfolios with positive payoffs exist.
Value of stock at expiry
Value at expiry
Слайд 3322.7 Valuing Options
The last section concerned itself with the value of
an option at expiry.
This section considers the value of an option prior to the expiration date.
A much more interesting question.
Слайд 34Option Value Determinants
Call Put
Stock price + –
Exercise price – +
Interest rate +
–
Volatility in the stock price + +
Expiration date + +
The value of a call option C0 must fall within
max (S0 – E, 0) < C0 < S0.
The precise position will depend on these factors.
Volatility in the stock price + +
Expiration date + +
The value of a call option C0 must fall within
max (S0 – E, 0) < C0 < S0.
The precise position will depend on these factors.
Слайд 35
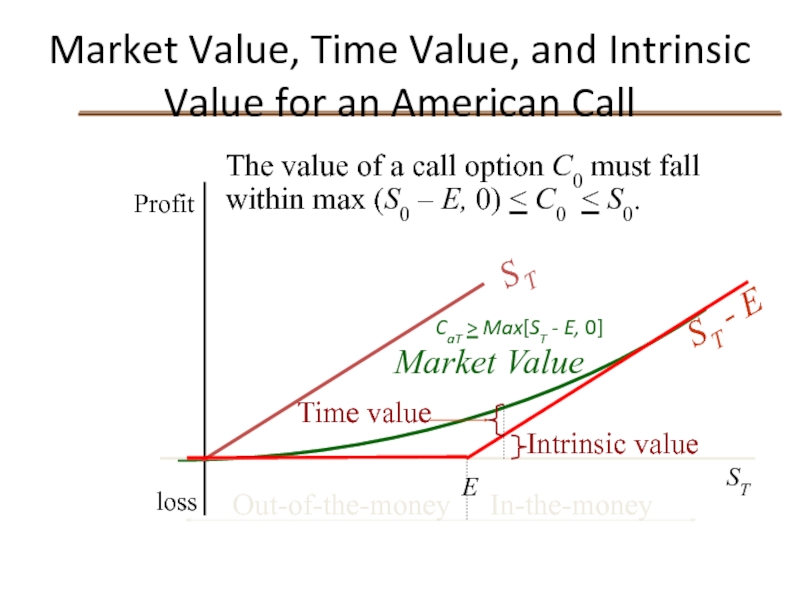
Market Value, Time Value, and Intrinsic Value for an American Call
CaT
> Max[ST - E, 0]
Profit
loss
E
ST
Market Value
Intrinsic value
ST - E
Time value
Out-of-the-money
In-the-money
ST
The value of a call option C0 must fall within max (S0 – E, 0) < C0 < S0.
Слайд 3622.8 An Option‑Pricing Formula
We will start with a binomial option pricing
formula to build our intuition.
Then we will graduate to the normal approximation to the binomial for some real-world option valuation.
Слайд 37
Binomial Option Pricing Model
Suppose a stock is worth $25 today and
in one period will either be worth 15% more or 15% less. S0= $25 today and in one year S1 is either $28.75 or $21.25. The risk-free rate is 5%. What is the value of an at-the-money call option?
$25
$21.25
$28.75
S1
S0
Слайд 38Binomial Option Pricing Model
A call option on this stock with exercise
price of $25 will have the following payoffs.
We can replicate the payoffs of the call option. With a levered position in the stock.
We can replicate the payoffs of the call option. With a levered position in the stock.
$25
$21.25
$28.75
S1
S0
C1
$3.75
$0
Слайд 39Binomial Option Pricing Model
Borrow the present value of $21.25 today and
buy one share.
The net payoff for this levered equity portfolio in one period is either $7.50 or $0.
The levered equity portfolio has twice the option’s payoff so the portfolio is worth twice the call option value.
The net payoff for this levered equity portfolio in one period is either $7.50 or $0.
The levered equity portfolio has twice the option’s payoff so the portfolio is worth twice the call option value.
$25
$21.25
$28.75
S1
S0
debt
- $21.25
portfolio
$7.50
$0
( - ) =
=
=
C1
$3.75
$0
- $21.25
Слайд 40Binomial Option Pricing Model
The levered equity portfolio value today
is today’s value of one share less the present value of a $21.25 debt:
$25
$21.25
$28.75
S1
S0
debt
- $21.25
portfolio
$7.50
$0
( - ) =
=
=
C1
$3.75
$0
- $21.25
Слайд 41Binomial Option Pricing Model
We can value the option today as half
of the value of the levered equity portfolio:
$25
$21.25
$28.75
S1
S0
debt
- $21.25
portfolio
$7.50
$0
( - ) =
=
=
C1
$3.75
$0
- $21.25
Слайд 42The Binomial Option Pricing Model
If the interest rate is 5%, the
call is worth:
$25
$21.25
$28.75
S1
S0
debt
- $21.25
portfolio
$7.50
$0
( - ) =
=
=
C1
$3.75
$0
- $21.25
Слайд 43The Binomial Option Pricing Model
If the interest rate is 5%, the
call is worth:
$25
$21.25
$28.75
S1
S0
debt
- $21.25
portfolio
$7.50
$0
( - ) =
=
=
C1
$3.75
$0
- $21.25
Слайд 44Binomial Option Pricing Model
the replicating portfolio intuition.
Many derivative securities can be
valued by valuing portfolios of primitive securities when those portfolios have the same payoffs as the derivative securities.
The most important lesson (so far) from the binomial option pricing model is:
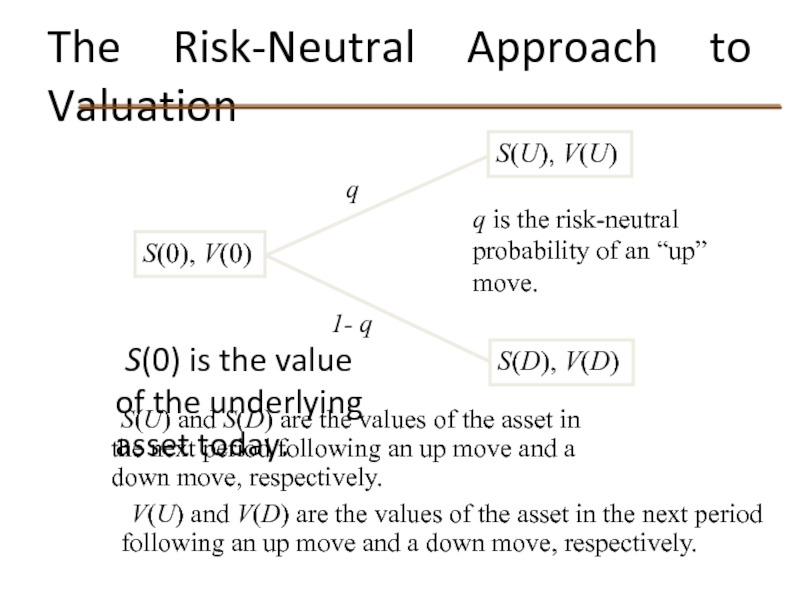
Слайд 45The Risk-Neutral Approach to Valuation
We could value V(0) as the value
of the replicating portfolio. An equivalent method is risk-neutral valuation
S(0), V(0)
S(U), V(U)
S(D), V(D)
q
1- q
Слайд 46
The Risk-Neutral Approach to Valuation
S(0) is the value of the underlying
asset today.
S(0), V(0)
S(U), V(U)
S(D), V(D)
S(U) and S(D) are the values of the asset in the next period following an up move and a down move, respectively.
q
1- q
V(U) and V(D) are the values of the asset in the next period following an up move and a down move, respectively.
q is the risk-neutral probability of an “up” move.
Слайд 47The Risk-Neutral Approach to Valuation
The key to finding q is to
note that it is already impounded into an observable security price: the value of S(0):
A minor bit of algebra yields:
Слайд 48Example of the Risk-Neutral Valuation of a Call:
Suppose a stock is
worth $25 today and in one period will either be worth 15% more or 15% less. The risk-free rate is 5%. What is the value of an at-the-money call option?
The binomial tree would look like this:
The binomial tree would look like this:
$21.25,C(D)
q
1- q
$25,C(0)
$28.75,C(D)
Слайд 49Example of the Risk-Neutral Valuation of a Call:
The next step would
be to compute the risk neutral probabilities
$21.25,C(D)
2/3
1/3
$25,C(0)
$28.75,C(D)
Слайд 50Example of the Risk-Neutral Valuation of a Call:
After that, find the
value of the call in the up state and down state.
$21.25, $0
2/3
1/3
$25,C(0)
$28.75, $3.75
Слайд 51Example of the Risk-Neutral Valuation of a Call:
Finally, find the value
of the call at time 0:
$25,$2.38
Слайд 52Risk-Neutral Valuation and the Replicating Portfolio
This risk-neutral result is consistent with
valuing the call using a replicating portfolio.
Слайд 53The Black-Scholes Model
The Black-Scholes Model is
Where
C0 = the value of a
European option at time t = 0
r = the risk-free interest rate.
N(d) = Probability that a standardized, normally distributed, random variable will be less than or equal to d.
The Black-Scholes Model allows us to value options in the real world just as we have done in the two-state world.
Слайд 54The Black-Scholes Model
Find the value of a six-month call option on
Microsoft with an exercise price of $150.
The current value of a share of Microsoft is $160.
The interest rate available in the U.S. is r = 5%.
The option maturity is six months (half of a year).
The volatility of the underlying asset is 30% per annum.
Before we start, note that the intrinsic value of the option is $10—our answer must be at least that amount.
The current value of a share of Microsoft is $160.
The interest rate available in the U.S. is r = 5%.
The option maturity is six months (half of a year).
The volatility of the underlying asset is 30% per annum.
Before we start, note that the intrinsic value of the option is $10—our answer must be at least that amount.
Слайд 55The Black-Scholes Model
Let’s try our hand at using the model. If
you have a calculator handy, follow along.
Then,
First calculate d1 and d2
Слайд 57Assume S = $50, X = $45, T = 6 months,
r = 10%,
and σ = 28%, calculate the value of a call and a put.
and σ = 28%, calculate the value of a call and a put.
From a standard normal probability table, look up N(d1) = 0.812 and N(d2) = 0.754 (or use Excel’s “normsdist” function)
Another Black-Scholes Example
Слайд 5822.9 Stocks and Bonds as Options
Levered Equity is a Call Option.
The
underlying asset comprises the assets of the firm.
The strike price is the payoff of the bond.
If at the maturity of their debt, the assets of the firm are greater in value than the debt, the shareholders have an in-the-money call, they will pay the bondholders, and “call in” the assets of the firm.
If at the maturity of the debt the shareholders have an out-of-the-money call, they will not pay the bondholders (i.e., the shareholders will declare bankruptcy), and let the call expire.
The strike price is the payoff of the bond.
If at the maturity of their debt, the assets of the firm are greater in value than the debt, the shareholders have an in-the-money call, they will pay the bondholders, and “call in” the assets of the firm.
If at the maturity of the debt the shareholders have an out-of-the-money call, they will not pay the bondholders (i.e., the shareholders will declare bankruptcy), and let the call expire.
Слайд 5922.9 Stocks and Bonds as Options
Levered Equity is a Put Option.
The
underlying asset comprise the assets of the firm.
The strike price is the payoff of the bond.
If at the maturity of their debt, the assets of the firm are less in value than the debt, shareholders have an in-the-money put.
They will put the firm to the bondholders.
If at the maturity of the debt the shareholders have an out-of-the-money put, they will not exercise the option (i.e., NOT declare bankruptcy) and let the put expire.
The strike price is the payoff of the bond.
If at the maturity of their debt, the assets of the firm are less in value than the debt, shareholders have an in-the-money put.
They will put the firm to the bondholders.
If at the maturity of the debt the shareholders have an out-of-the-money put, they will not exercise the option (i.e., NOT declare bankruptcy) and let the put expire.
Слайд 6022.9 Stocks and Bonds as Options
It all comes down to put-call
parity.
Stockholder’s position in terms of call options
Stockholder’s position in terms of put options
Слайд 6122.10 Capital-Structure Policy and Options
Recall some of the agency costs of
debt: they can all be seen in terms of options.
For example, recall the incentive shareholders in a levered firm have to take large risks.
For example, recall the incentive shareholders in a levered firm have to take large risks.
Слайд 62Balance Sheet for a Company in Distress
Assets BV MV Liabilities BV MV
Cash $200 $200 LT bonds $300 ?
Fixed Asset $400 $0 Equity $300 ?
Total $600 $200 Total $600 $200
What happens if
the firm is liquidated today?
The bondholders get $200; the shareholders get nothing.
Слайд 63
Selfish Strategy 1: Take Large Risks
(Think of a Call Option)
The
Gamble Probability Payoff
Win Big 10% $1,000
Lose Big 90% $0
Cost of investment is $200 (all the firm’s cash)
Required return is 50%
Expected CF from the Gamble = $1000 × 0.10 + $0 = $100
Win Big 10% $1,000
Lose Big 90% $0
Cost of investment is $200 (all the firm’s cash)
Required return is 50%
Expected CF from the Gamble = $1000 × 0.10 + $0 = $100
Слайд 64
Selfish Stockholders Accept Negative NPV Project with Large Risks
Expected cash flow
from the Gamble
To Bondholders = $300 × 0.10 + $0 = $30
To Stockholders = ($1000 - $300) × 0.10 + $0 = $70
PV of Bonds Without the Gamble = $200
PV of Stocks Without the Gamble = $0
PV of Bonds With the Gamble = $30 / 1.5 = $20
PV of Stocks With the Gamble = $70 / 1.5 = $47
To Bondholders = $300 × 0.10 + $0 = $30
To Stockholders = ($1000 - $300) × 0.10 + $0 = $70
PV of Bonds Without the Gamble = $200
PV of Stocks Without the Gamble = $0
PV of Bonds With the Gamble = $30 / 1.5 = $20
PV of Stocks With the Gamble = $70 / 1.5 = $47
The stocks are worth more with the high risk project because the call option that the shareholders of the levered firm hold is worth more when the volatility is increased.
Слайд 6522.11 Mergers and Options
This is an area rich with optionality, both
in the structuring of the deals and in their execution.
Слайд 6622.12 Investment in Real Projects & Options
Classic NPV calculations typically ignore
the flexibility that real-world firms typically have.
The next chapter will take up this point.
The next chapter will take up this point.
Слайд 6722.13 Summary and Conclusions
The most familiar options are puts and calls.
Put
options give the holder the right to sell stock at a set price for a given amount of time.
Call options give the holder the right to buy stock at a set price for a given amount of time.
Put-Call parity
Call options give the holder the right to buy stock at a set price for a given amount of time.
Put-Call parity
Слайд 6822.13 Summary and Conclusions
The value of a stock option depends on
six factors:
1. Current price of underlying stock.
2. Dividend yield of the underlying stock.
3. Strike price specified in the option contract.
4. Risk-free interest rate over the life of the contract.
5. Time remaining until the option contract expires.
6. Price volatility of the underlying stock.
Much of corporate financial theory can be presented in terms of options.
Common stock in a levered firm can be viewed as a call option on the assets of the firm.
Real projects often have hidden options that enhance value.
1. Current price of underlying stock.
2. Dividend yield of the underlying stock.
3. Strike price specified in the option contract.
4. Risk-free interest rate over the life of the contract.
5. Time remaining until the option contract expires.
6. Price volatility of the underlying stock.
Much of corporate financial theory can be presented in terms of options.
Common stock in a levered firm can be viewed as a call option on the assets of the firm.
Real projects often have hidden options that enhance value.
