- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование социально-экономических процессов презентация
Содержание
- 1. Моделирование социально-экономических процессов
- 2. 1. Математические модели в макроэкономике
- 3. 1.1 Классификация экономико-математических моделей
- 5. экономическая
- 19. 1.2. Секторные модели макроэкономики
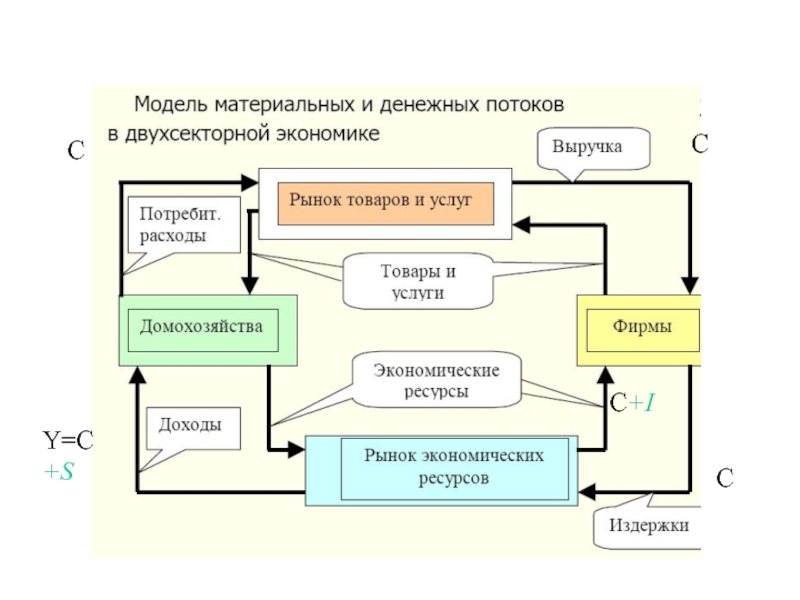
- 24. С Y=C+S C+I C C
- 25. В двухсекторной модели экономики, изображенной на рисунке
- 26. Следует отметить, что поскольку домохозяйства действуют рационально,
- 27. Совокупные расходы - непроизводственное потребление и инвестиционные
- 28. Описанная ситуация предопределяет возможность появления финансового рынка
- 29. В трехсекторную модель экономики наряду с домохозяйствами
- 30. В состоянии равновесия: В трехсекторной модели
- 31. Включение в схему кругооборота иностранного сектора дает
- 32. В состоянии равновесия В четырехсекторной модели должно выполняться основное макроэкономическое тождество
- 33. 2. Моделирование процесса производства
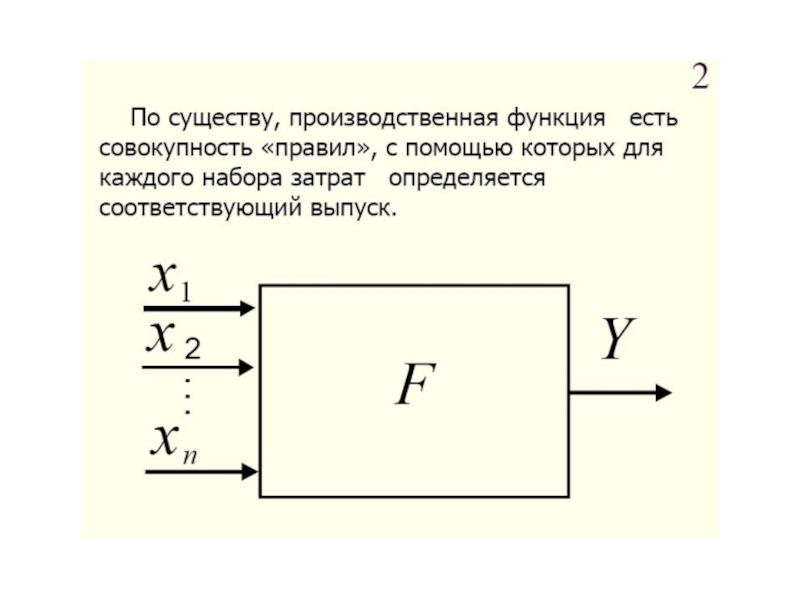
- 34. 2.1. Производственные функции и их свойства
- 37. Неоклассическая производственная функция обладает следующими свойствами:
- 40. 5. Производственная функция должна обладать свойством масштабируемости
- 41. Напомним, что A и α в этой
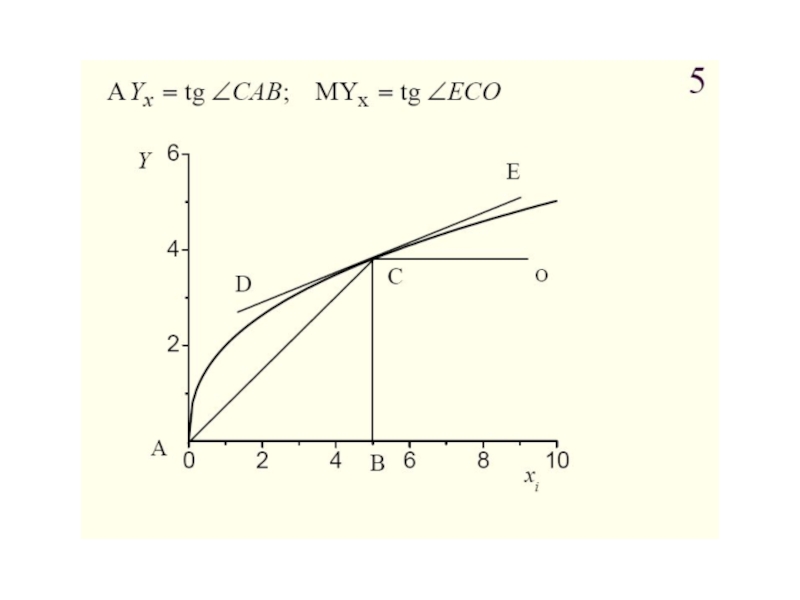
- 44. Характеристики производственной функции
- 58. 2.2. Производственные функции с постоянной эластичностью замещения факторов производства
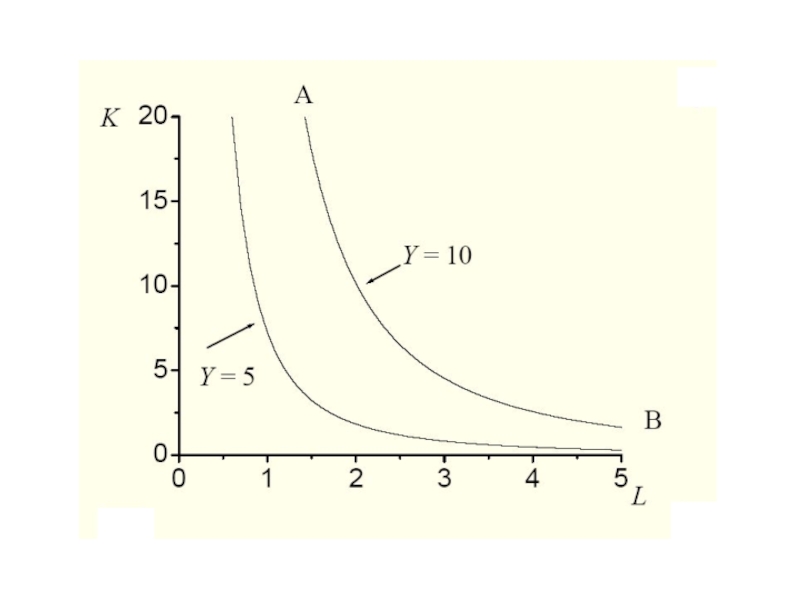
- 59. Замещение ресурсов в процессе производства
- 60. Рассмотрим производственную функцию из предыдущего примера: Мы можем зафиксировать выпуск на некотором уровне Y0.
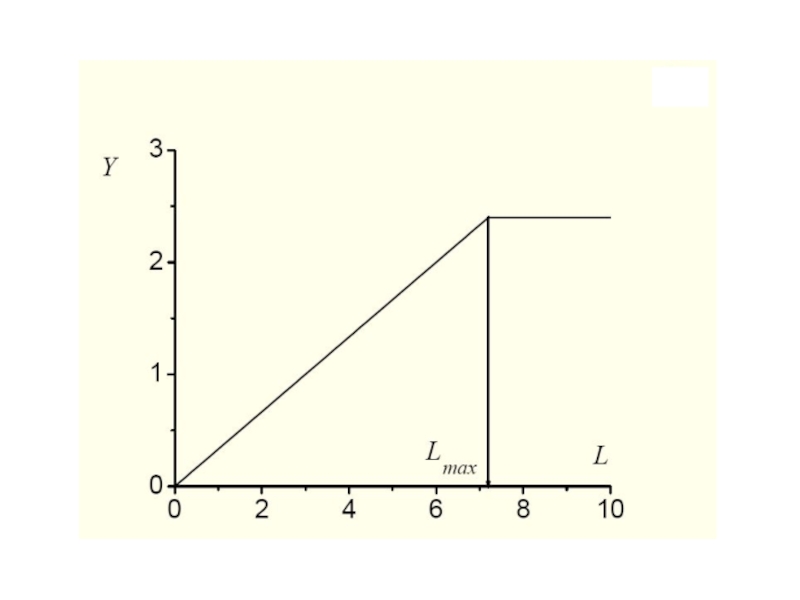
- 67. Если в процессе производства замена одного фактора
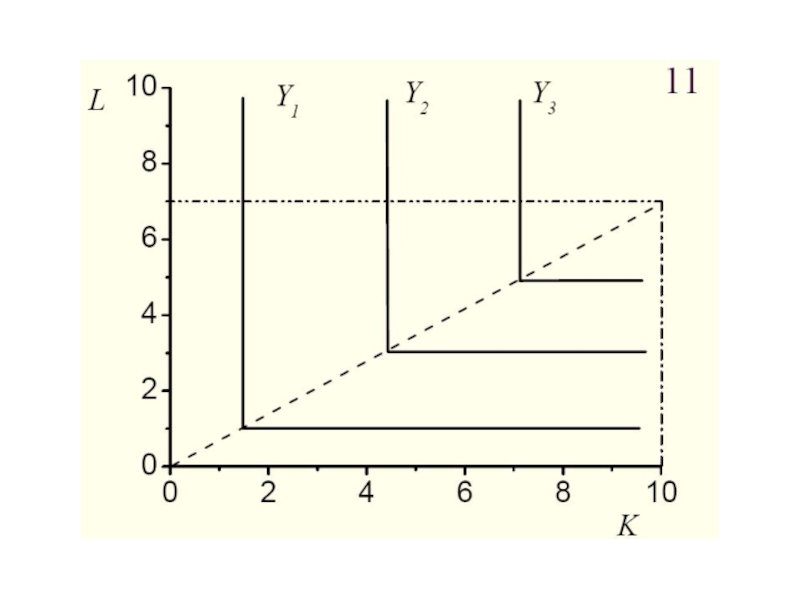
- 68. Чтобы построить множество изоквант производственной функции Леонтьева,
- 73. Предельная норма замещения факторов производства
- 74. Предельную норму замещения одного фактора производства другим
- 75. Полученную формулу предельной нормы замещения факторов
- 76. Предельная норма замещения труда капиталом показывает, какое
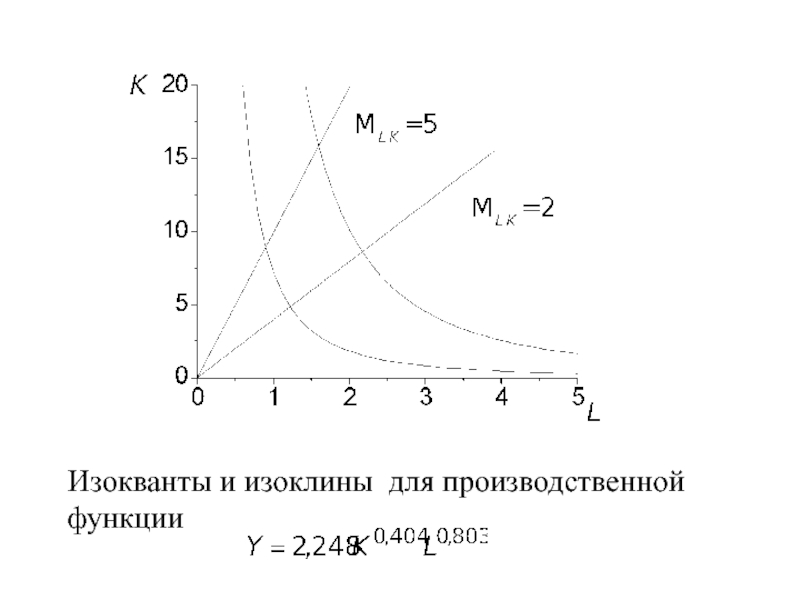
- 77. Предельная норма замещения труда капиталом прямо пропорциональна
- 78. Изокванты и изоклины для производственной функции
- 79. Эластичность замещения труда капиталом равна величине относительного
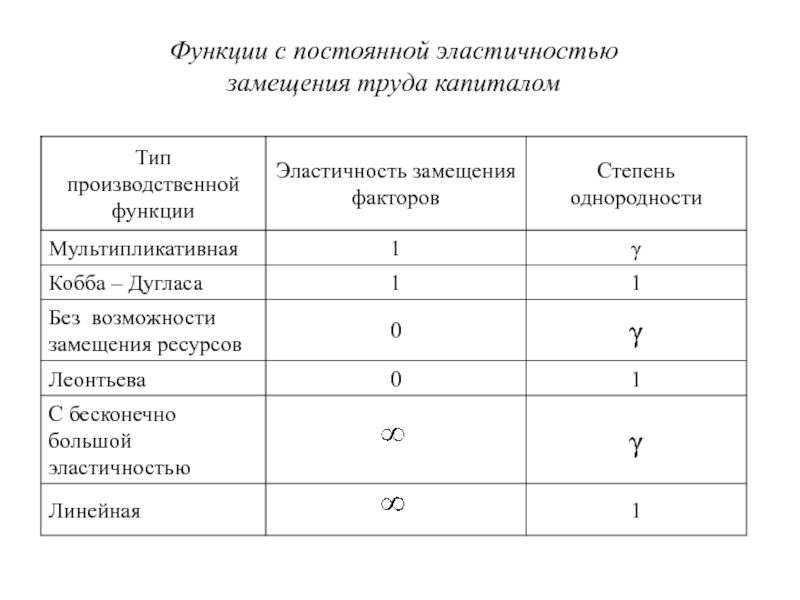
- 80. Функции с постоянной эластичностью замещения труда капиталом
- 81. Без возможности замещения ресурсов С бесконечно большой эластичностью Линейная
- 82. 2.3. Модель В. Леонтьева «Затраты - выпуск»
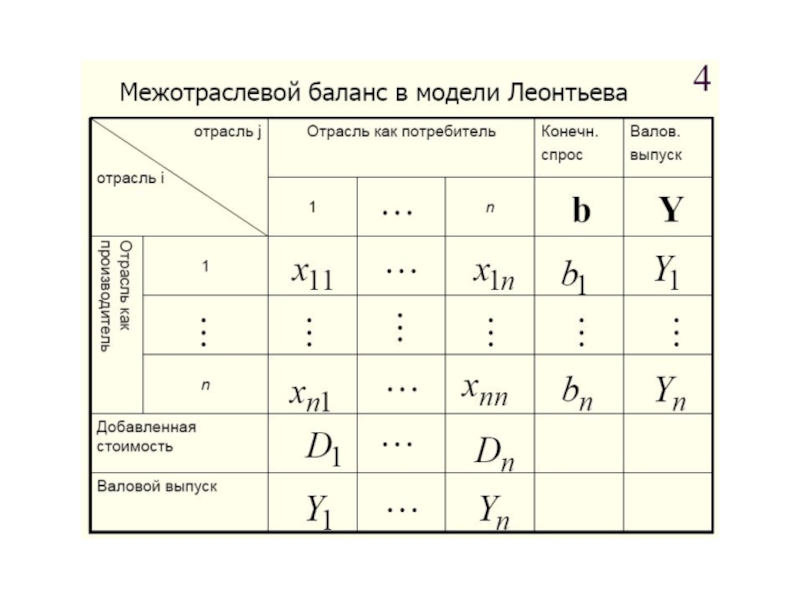
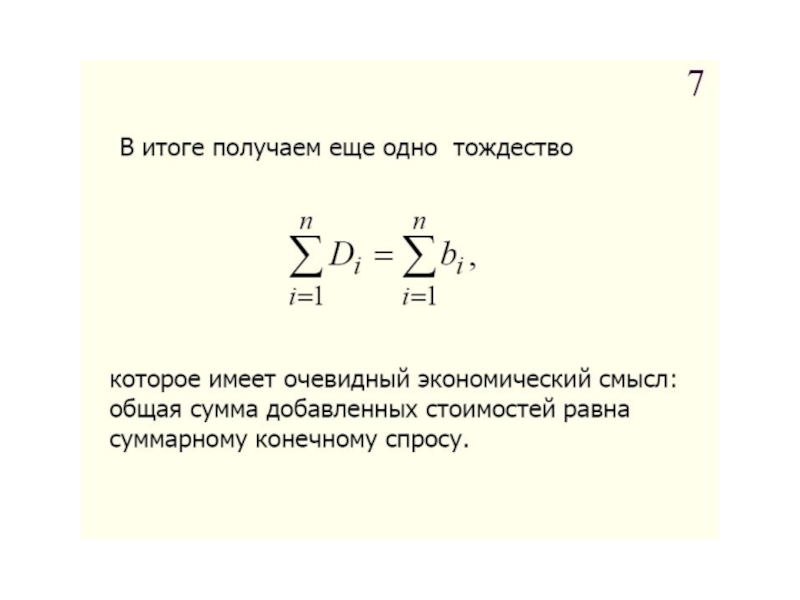
- 98. Таблица и тождества межотраслевого баланса
Слайд 1Моделирование социально-экономических процессов
доц. Гусева В. Б., кафедра информатики и математики. к.307
Размещение
Слайд 25В двухсекторной модели экономики, изображенной на рисунке предполагается, что:
Стоимость каждого
2. Совокупные расходы домохозяйств (потребление С) равны их совокупным доходам;
3. Национальный доход равен национальному продукту (Y);
4. Совокупный спрос равен совокупному предложению (фирмы продают все, что произвели, без остатка);
Описанная модель может быть представлена уравнением Y=C
Слайд 26Следует отметить, что поскольку домохозяйства действуют рационально, то они обычно тратят
С другой стороны, каждая фирмы испытывают постоянную необходимость вкладывать хотя бы небольшую часть средств в производство, обеспечивая его существование и расширение.
Слайд 27Совокупные расходы - непроизводственное потребление и инвестиционные расходы
Национальный доход -
В состоянии равновесия:
Слайд 28Описанная ситуация предопределяет возможность появления финансового рынка
Домохозяйства предоставляют свои сбережения
2. Домохозяйства тратят свои сбережения на покупку ценных бумаг, выпускаемых фирмами, напрямую обеспечивая их инвестиционными ресурсами.
Слайд 29В трехсекторную модель экономики наряду с домохозяйствами и предпринимателями включается государственный
Совокупные расходы состоят теперь из трех компонентов: потребления , инвестиций и государственных закупок :
Совокупный доход распределяется на потребление, сбережения и налоги:
Слайд 30В состоянии равновесия:
В трехсекторной модели национальный доход, являющийся доходом, заработанным собственниками
Слайд 31Включение в схему кругооборота иностранного сектора дает четырехсекторную модель экономики (модель
Расходы иностранного сектора носят название чистого экспорта и представляют собой разницу между экспортом и импортом
Слайд 32В состоянии равновесия
В четырехсекторной модели должно выполняться основное макроэкономическое тождество
Слайд 405. Производственная функция должна обладать свойством масштабируемости (при увеличении объема всех
*
Слайд 41Напомним, что A и α в этой функции – константы, характеризующие
Еще один пример – мультипликативная производственная функция
Y=AKαLβ
Слайд 60Рассмотрим производственную функцию из предыдущего примера:
Мы можем зафиксировать выпуск на некотором
Слайд 67Если в процессе производства замена одного фактора другим невозможна, для его
Коэффициенты c1 и с2 зависят от количества ресурса, необходимого для производства единицы товара (a, b).
Слайд 68Чтобы построить множество изоквант производственной функции Леонтьева, необходимо сначала построить прямую
Слайд 74Предельную норму замещения одного фактора производства другим определим соотношением
Рассмотрим производственную
Слайд 75
Полученную формулу предельной нормы замещения факторов производства можно записать, используя определение
Слайд 76Предельная норма замещения труда капиталом показывает, какое дополнительное количество капитала может
Предельная норма замещения труда капиталом численно равна тангенсу угла наклона касательной к изокванте.
Слайд 77Предельная норма замещения труда капиталом прямо пропорциональна фондовооруженности k=K/L
При условии постоянства
Слайд 79Эластичность замещения труда капиталом равна величине относительного изменения фондовооруженности в условиях