- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические методы в экономике презентация
Содержание
- 1. Математические методы в экономике
- 2. БАЗОВЫЙ УЧЕБНИК
- 3. История вопроса
- 4. История вопроса
- 5. История вопроса
- 6. Понятие о модели и моделировании
- 7. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
- 8. Математическая модель
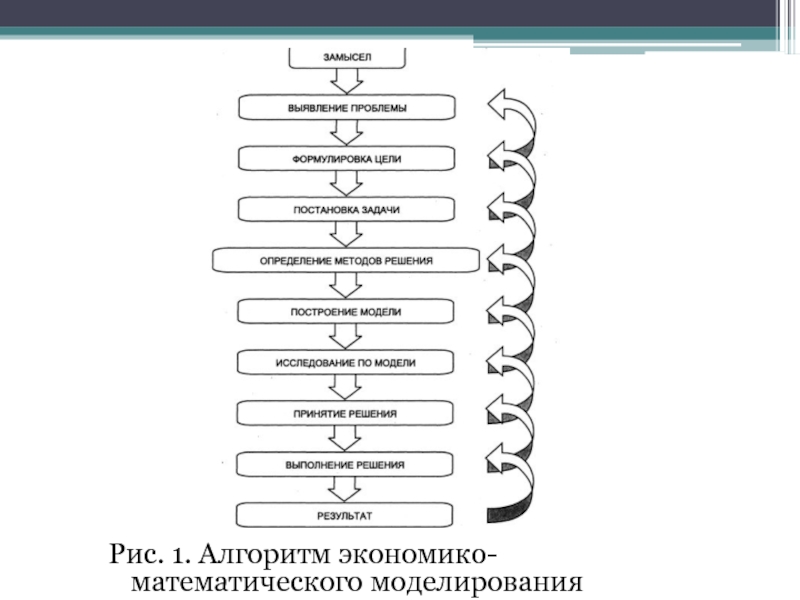
- 9. Рис. 1. Алгоритм экономико-математического моделирования
- 11. продолжение
- 12. Цель и критерии моделирования
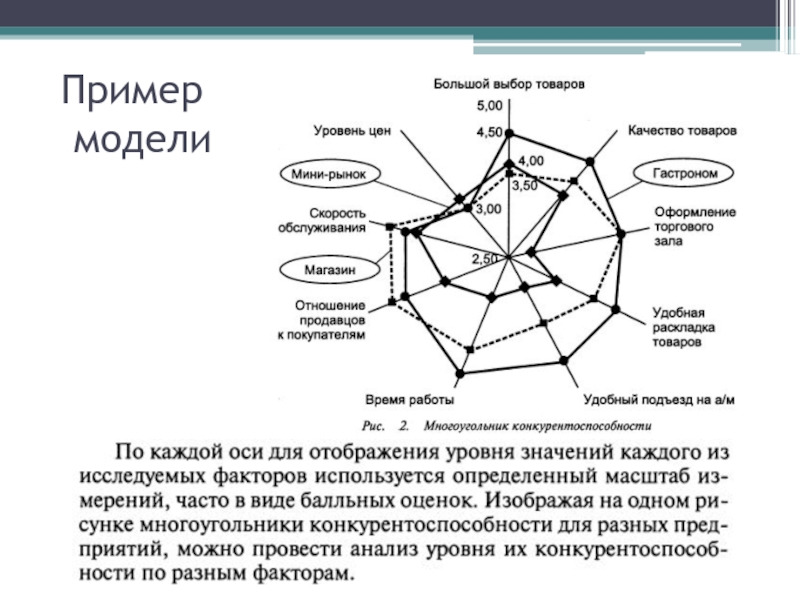
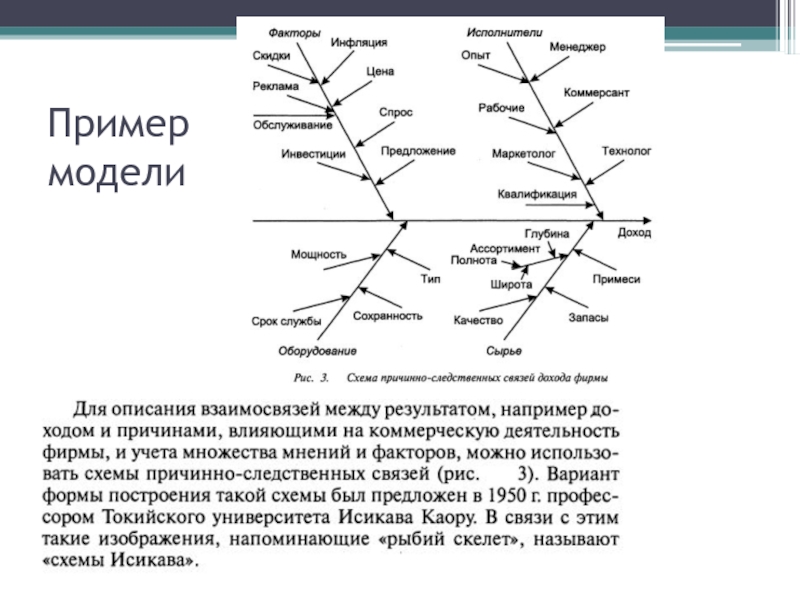
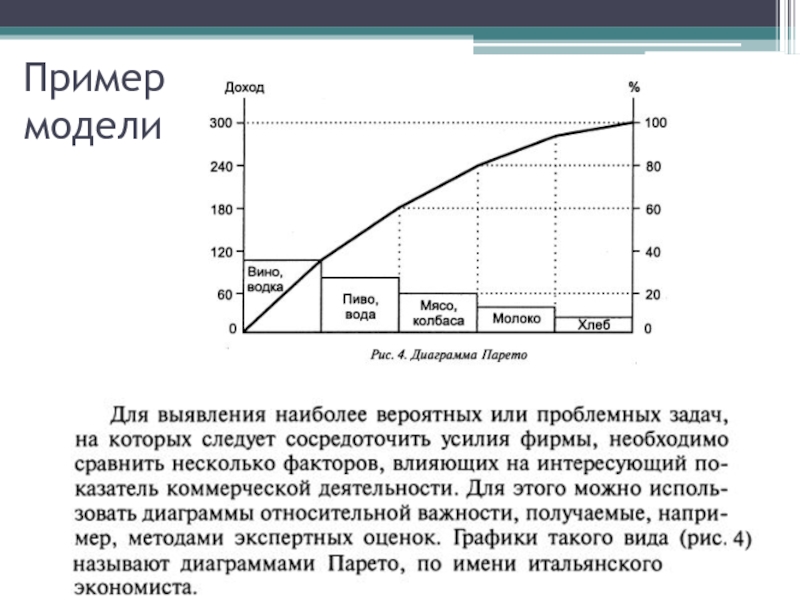
- 13. Пример модели
- 14. Пример модели
- 15. Пример модели
- 16. Специальная модель - производственная функция
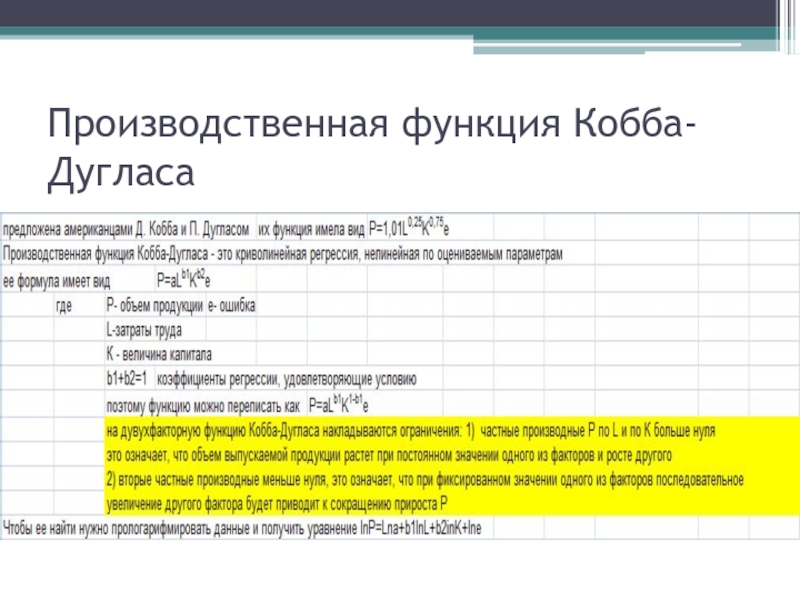
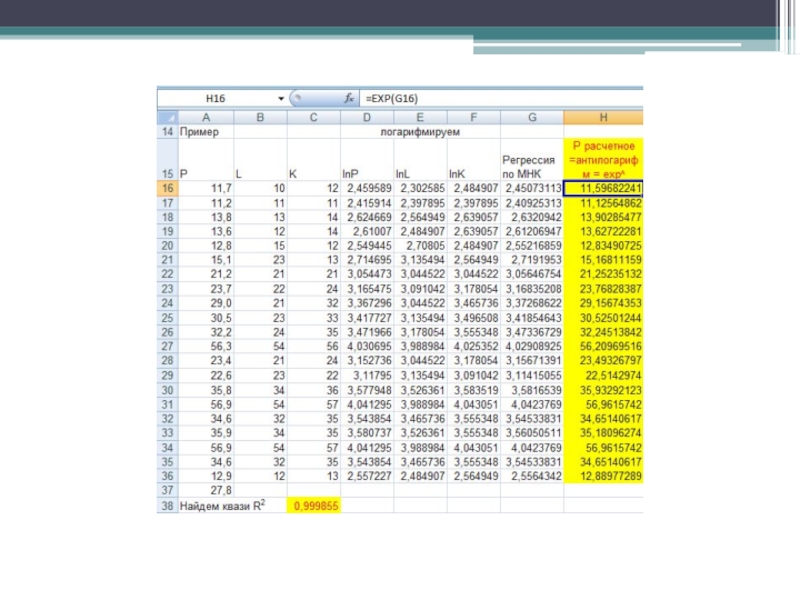
- 17. Производственная функция Кобба-Дугласа
- 19. Специальная модель - функция потребления
- 23. Математическое моделирование задач экономической (коммерческой) деятельности Особенности
- 25. ПОНЯТИЕ ЦЕЛЕВОЙ ФУНКЦИИ
- 27. Общая постановка задачи принятия решения включает: Задание цели; Средств достижения цели; Оценка результата
- 28. Математическая модель принятия решения Формализованное описание цели,
- 29. Если множества альтернатив и состояний
- 30. Целевая функция в виде матрицы
- 31. РЕШЕНИЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЯ В УСЛОВИЯХ ОПРЕДЕЛЕННОСТИ
- 32. Пример: решение задачи распределения коммерсантов по операциям (дан хронометраж по затратам времени на операцию)
- 33. Критерий эффективности: общее число человеко-часов на все операции (Т)
- 35. Если увеличивается число вариантов принятия решения (число
- 37. РЕШЕНИЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЯ ПРИ ЗАДАНИИ ОТНОШЕНИЙ
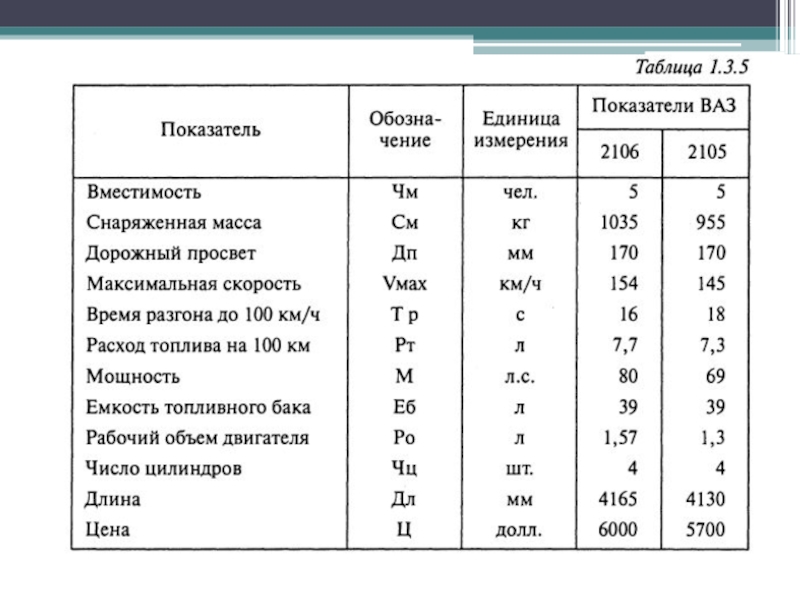
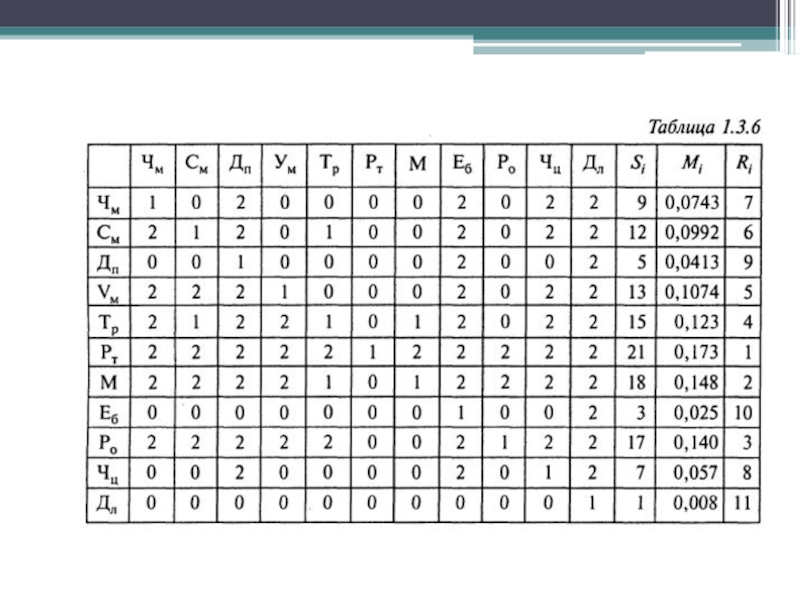
- 47. Расчет интегральных оценок F(2105) =0,0743*1+0,0992*1+0,413*1+0,1074*2+0,123*2+0,173*1+0,148*1+0,025* 2+0,14*2+0,057*1+0,08*2=1,4754 F(2106)
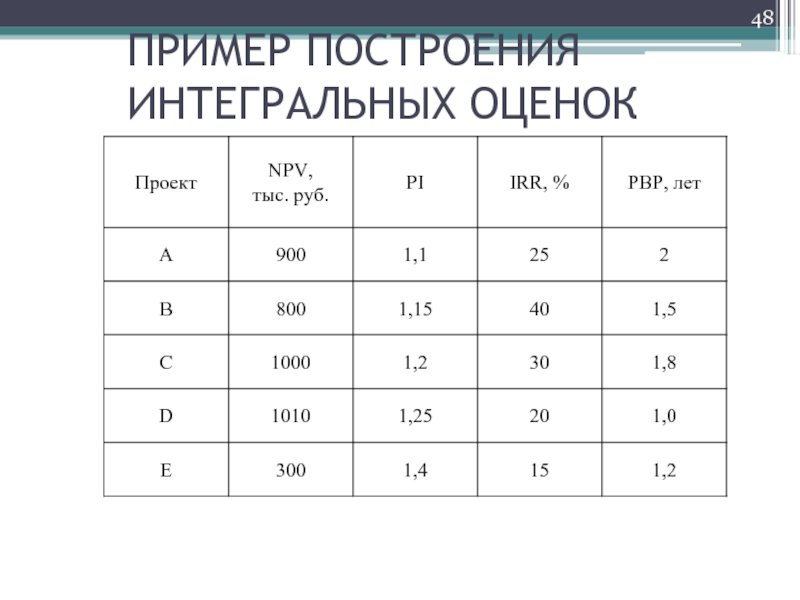
- 48. ПРИМЕР ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ОЦЕНОК
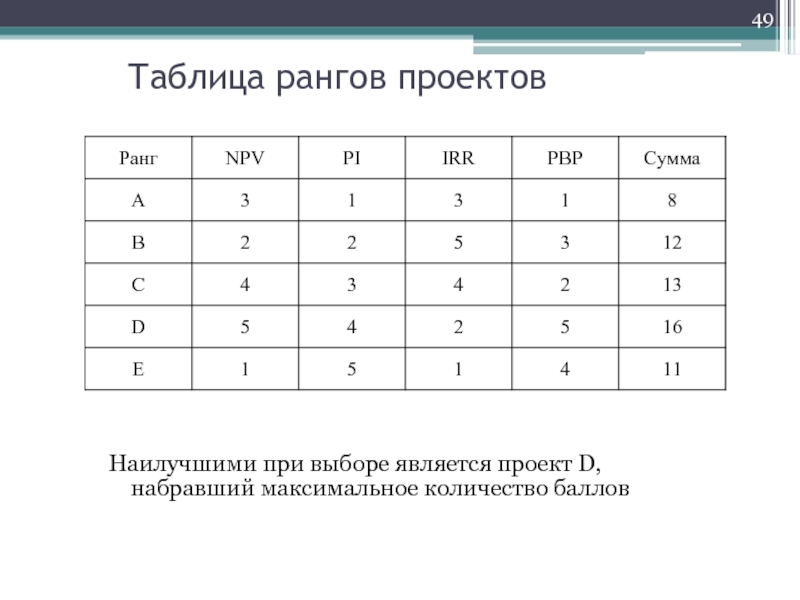
- 49. Таблица рангов проектов Наилучшими при выборе является проект D, набравший максимальное количество баллов
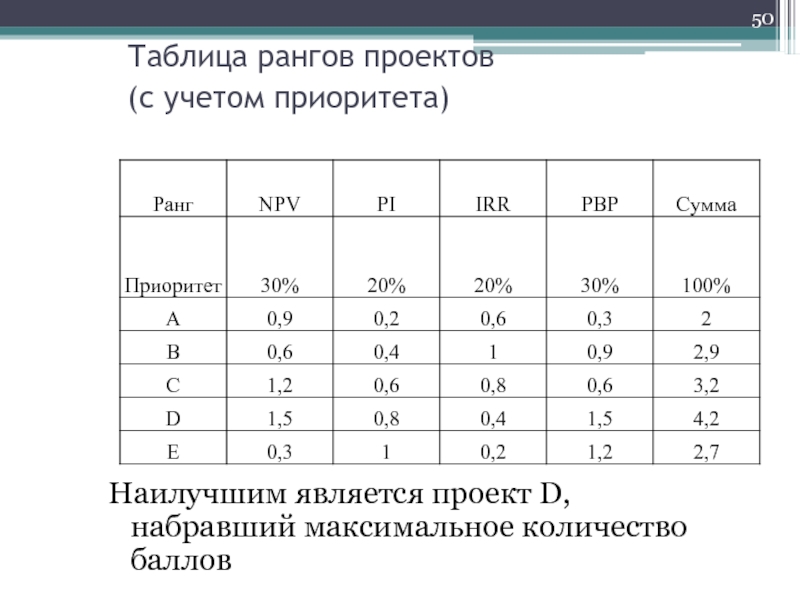
- 50. Таблица рангов проектов (с учетом приоритета)
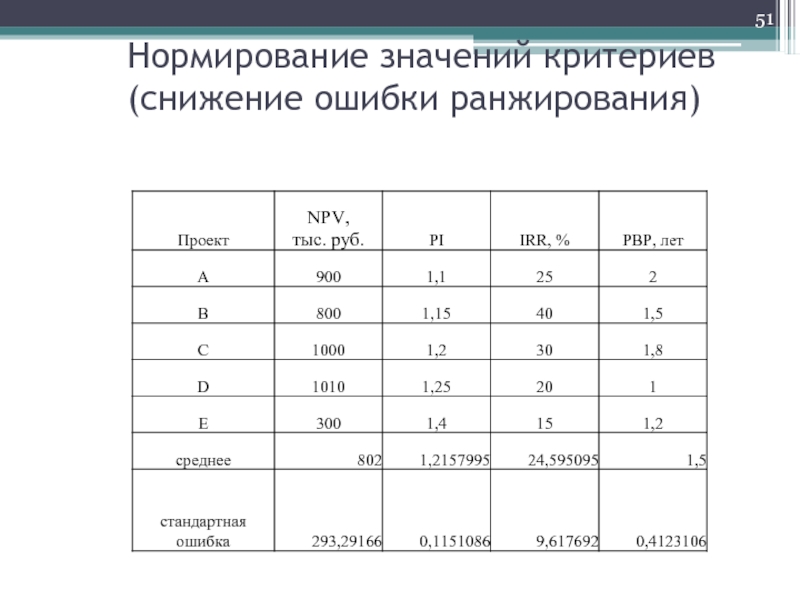
- 51. Нормирование значений критериев (снижение ошибки ранжирования)
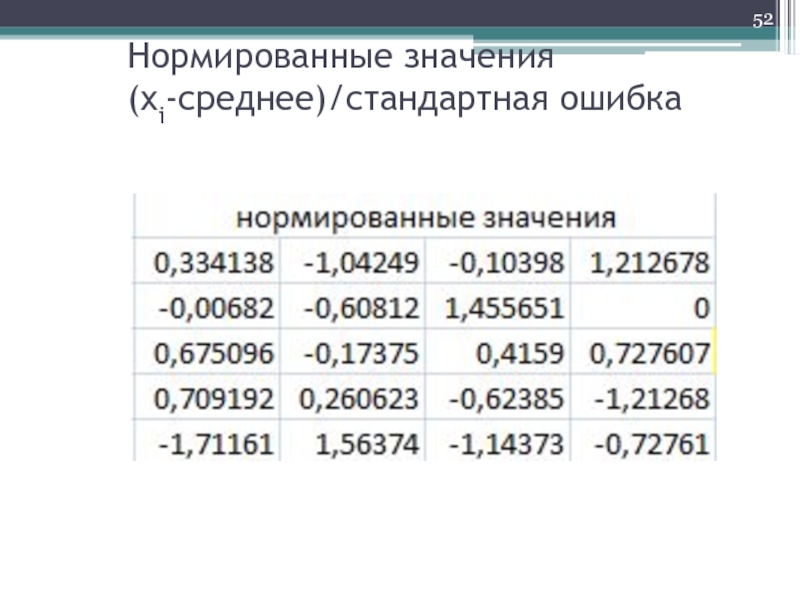
- 52. Нормированные значения (xi-среднее)/стандартная ошибка
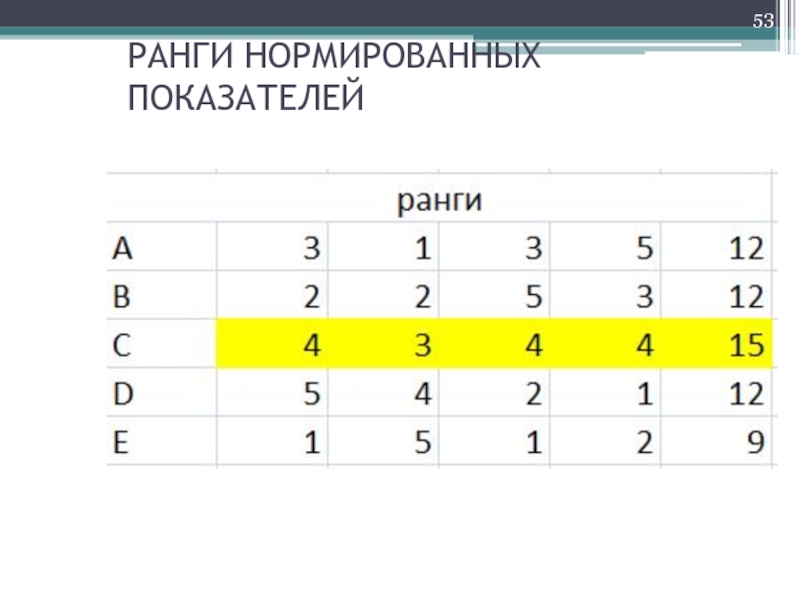
- 53. РАНГИ НОРМИРОВАННЫХ ПОКАЗАТЕЛЕЙ
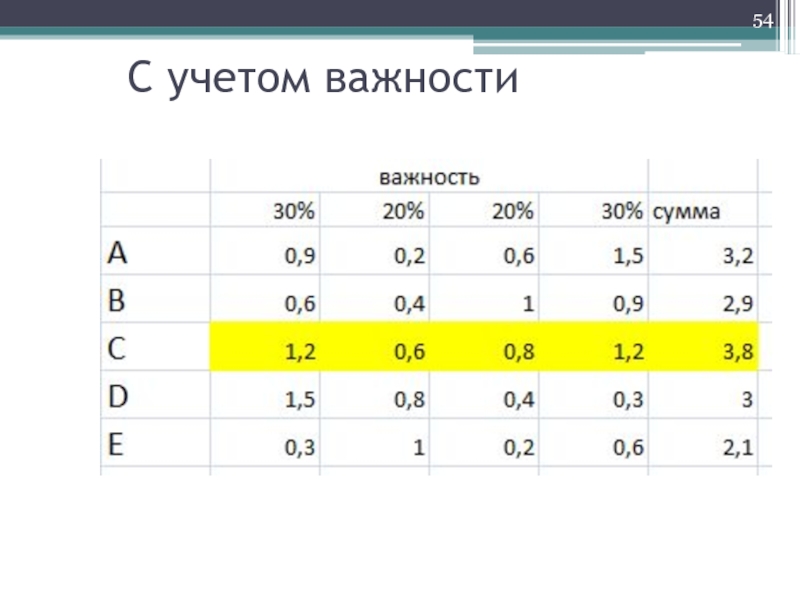
- 54. С учетом важности
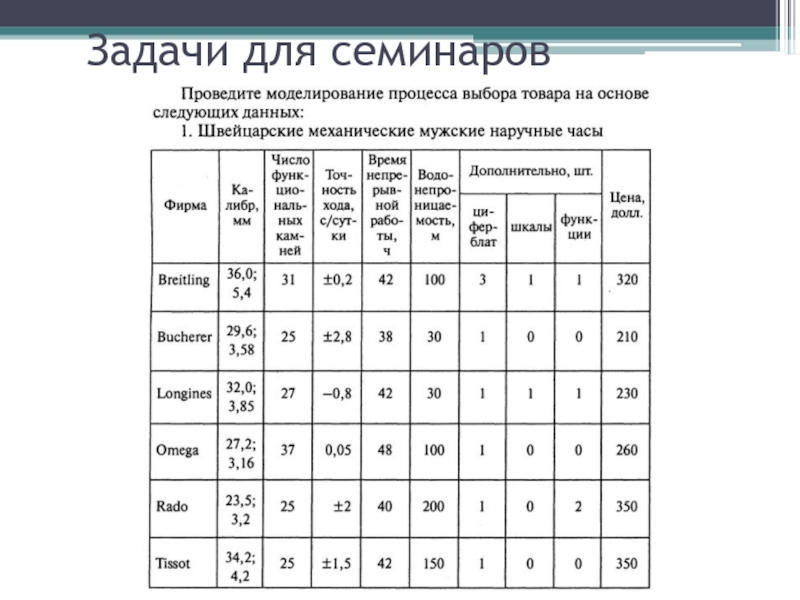
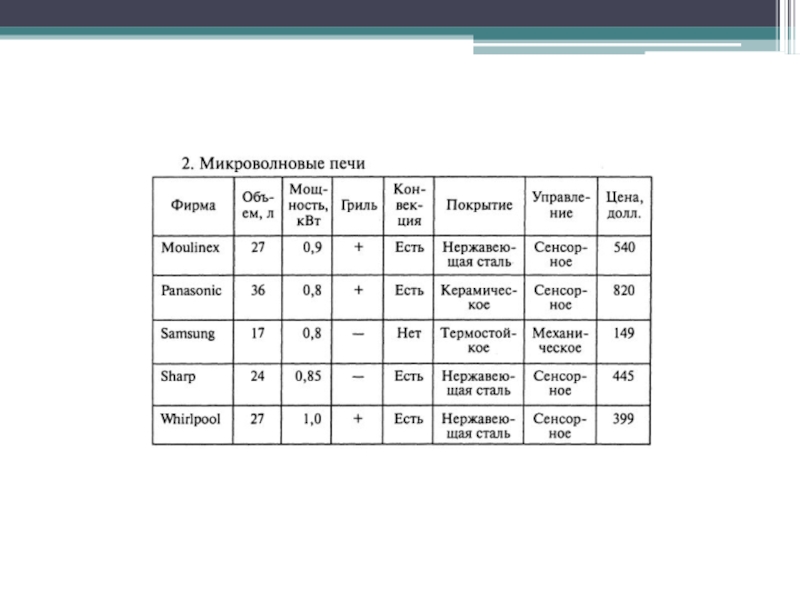
- 55. Задачи для семинаров
Слайд 1МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ
К.э.н., доцент
и.о. зав. каф. ЭЭММИ
Бурцева Татьяна Александровна
Слайд 23Математическое моделирование задач экономической (коммерческой) деятельности
Особенности данной деятельности определяющие необходимость применения
математического моделирования
Системность
Многофакторность
Многовариантность
Необходимость обеспечения оптимальности при принятии решений
Системность
Многофакторность
Многовариантность
Необходимость обеспечения оптимальности при принятии решений
Слайд 27Общая постановка задачи принятия решения включает:
Задание цели;
Средств достижения цели;
Оценка результата
Слайд 28Математическая модель принятия решения
Формализованное описание цели, средств, результатов и способа связи
между средствами и результатами.
Слайд 29 Если множества альтернатив и состояний конечны: то целевую функцию F можно
представить в матричном виде
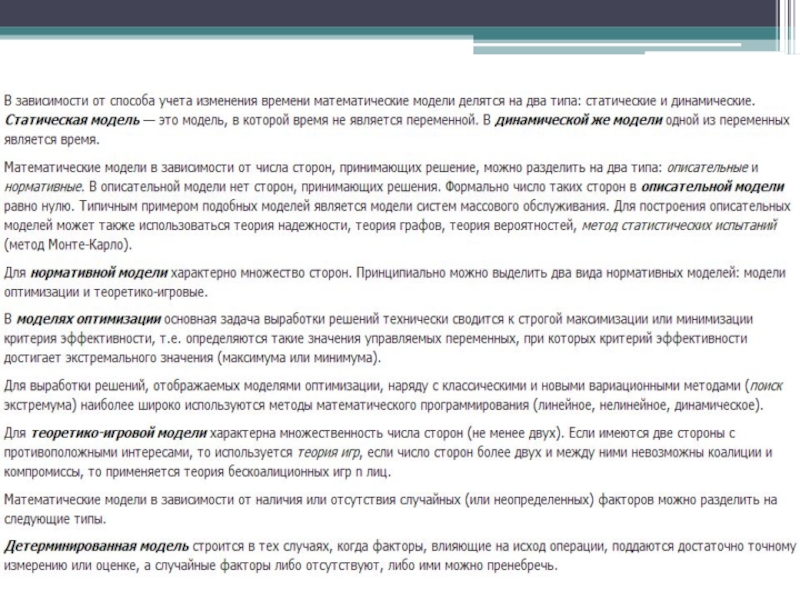
Слайд 31РЕШЕНИЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЯ В УСЛОВИЯХ ОПРЕДЕЛЕННОСТИ
Существует детерминированная связь между принятием
решения и результатом, поэтому задачи называются детерминированными
Существует единственное оптимальное решение и оно может быть определено с помощью нахождения экстремума целевой функции
Существует единственное оптимальное решение и оно может быть определено с помощью нахождения экстремума целевой функции
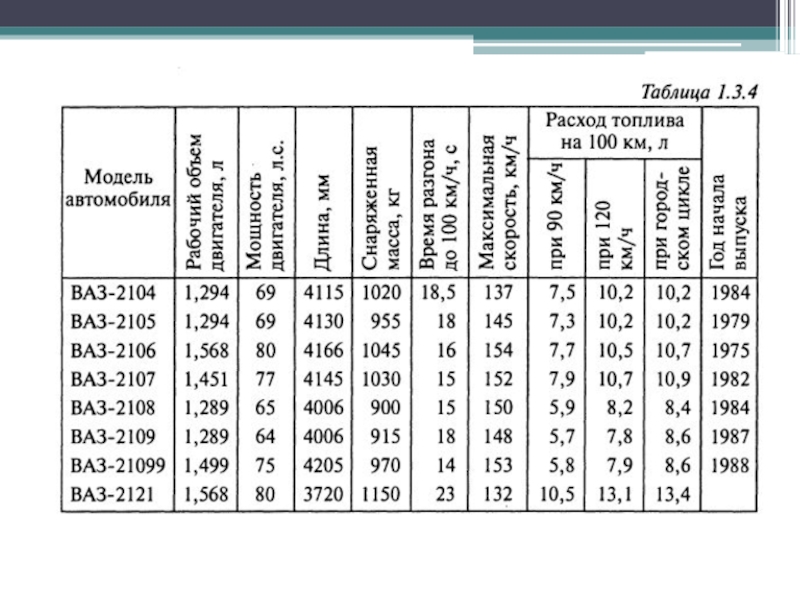
Слайд 32Пример: решение задачи распределения коммерсантов по операциям (дан хронометраж по затратам
времени на операцию)
Слайд 35Если увеличивается число вариантов принятия решения (число стратегий, то есть растет
n!), то уже нужно применять сложные методы, в данном случае методы линейного программирования
Слайд 37РЕШЕНИЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЯ ПРИ ЗАДАНИИ ОТНОШЕНИЙ ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ
Вводят
количественный критерий, позволяющий задать отношения предпочтения (прибыль, издержки, доход и т.п.)
Слайд 47Расчет интегральных оценок
F(2105) =0,0743*1+0,0992*1+0,413*1+0,1074*2+0,123*2+0,173*1+0,148*1+0,025* 2+0,14*2+0,057*1+0,08*2=1,4754
F(2106) =0,0743*1+0,0992*2+0,413*1+0,1074*1+0,123*1+0,173*2+0,148*1+0,025* 1+0,14*1+0,057*1+0,08*1=1,2722
Так как лучшему меньший ранг,
то 2106 лучше
Слайд 49Таблица рангов проектов
Наилучшими при выборе является проект D, набравший максимальное количество
баллов
Слайд 50Таблица рангов проектов
(с учетом приоритета)
Наилучшим является проект D, набравший
максимальное количество баллов