- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Lecture # 09. Inputs and Production Functions презентация
Содержание
- 1. Lecture # 09. Inputs and Production Functions
- 2. Outline The Production Function Marginal and Average
- 3. Definitions Inputs or factors of production are
- 4. Definitions Production transforms a set of inputs
- 5. Definitions The production function tells us the
- 6. Definitions A technically efficient firm is attaining
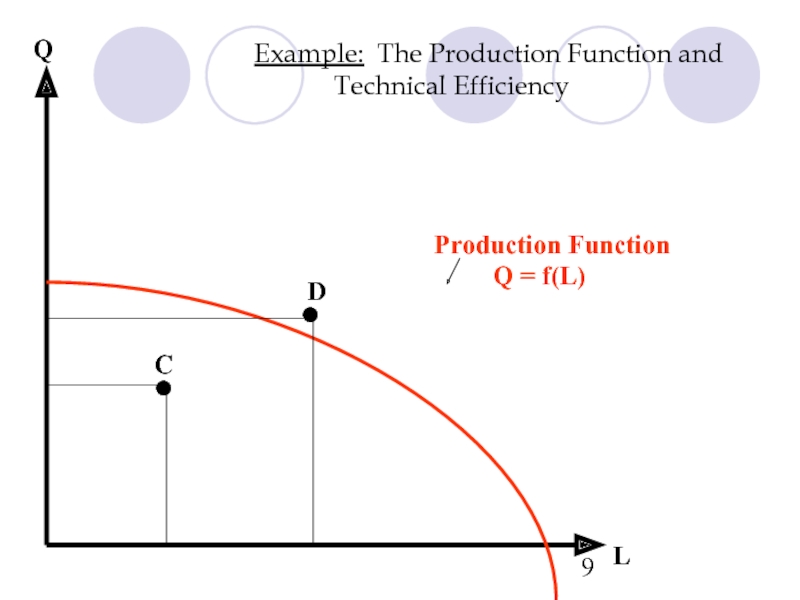
- 7. Example: The Production Function and Technical Efficiency L Q • C
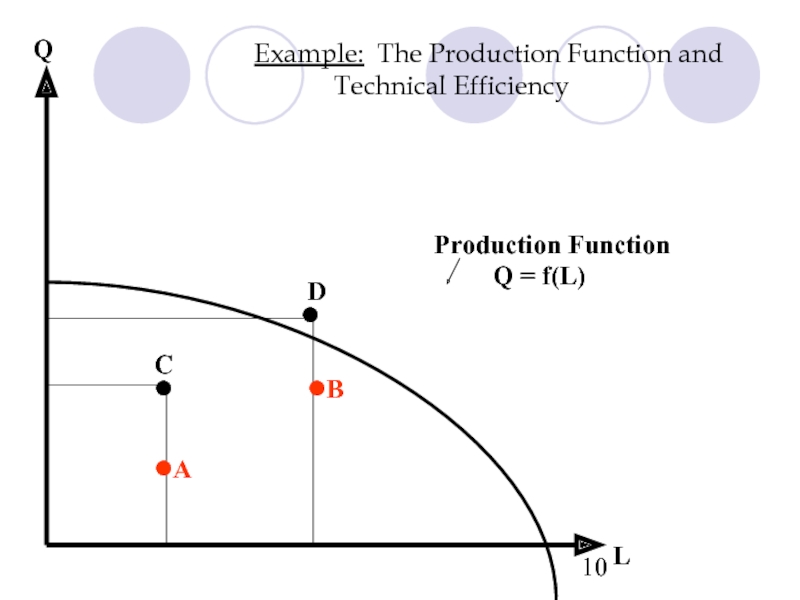
- 8. Example: The Production Function and Technical Efficiency L Q • • C D
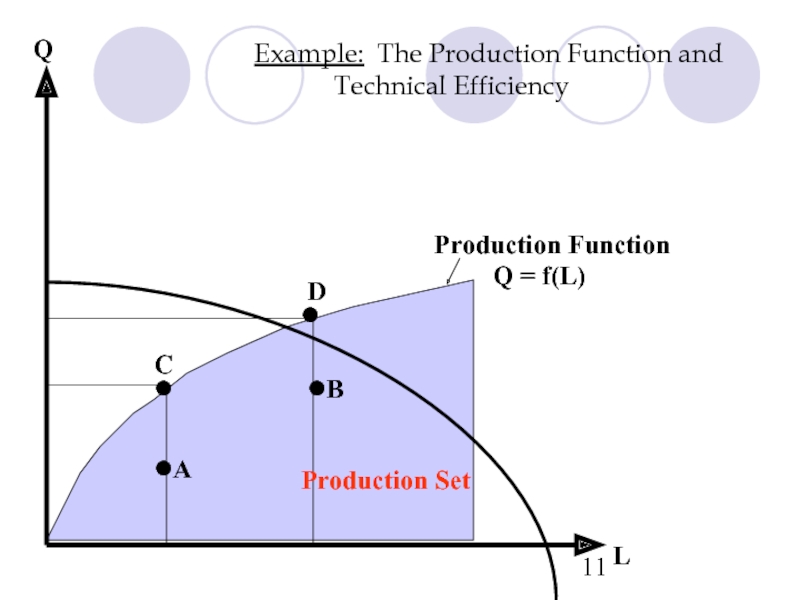
- 9. Example: The Production Function and Technical Efficiency
- 10. Example: The Production Function and Technical Efficiency
- 11. Example: The Production Function and Technical
- 12. Notes: The variables in the production function
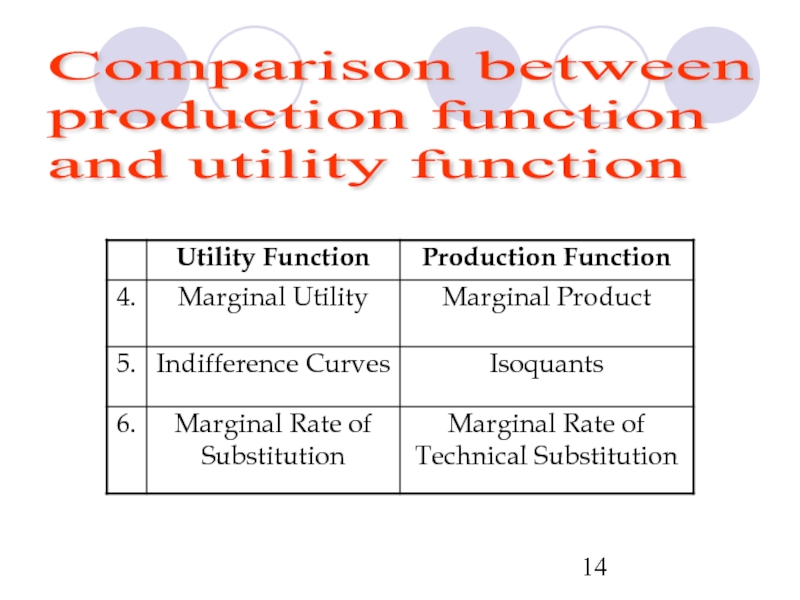
- 13. Comparison between production function and utility function
- 14. Comparison between production function and utility function
- 15. Marginal Product Definition: The marginal product of
- 16. Example: Suppose Q = K0.5L0.5 Then:
- 17. Average Product Definition: The average product of
- 18. Example: Suppose Q = K0.5L0.5 Then:
- 19. Law of Diminishing Marginal Returns Definition: The
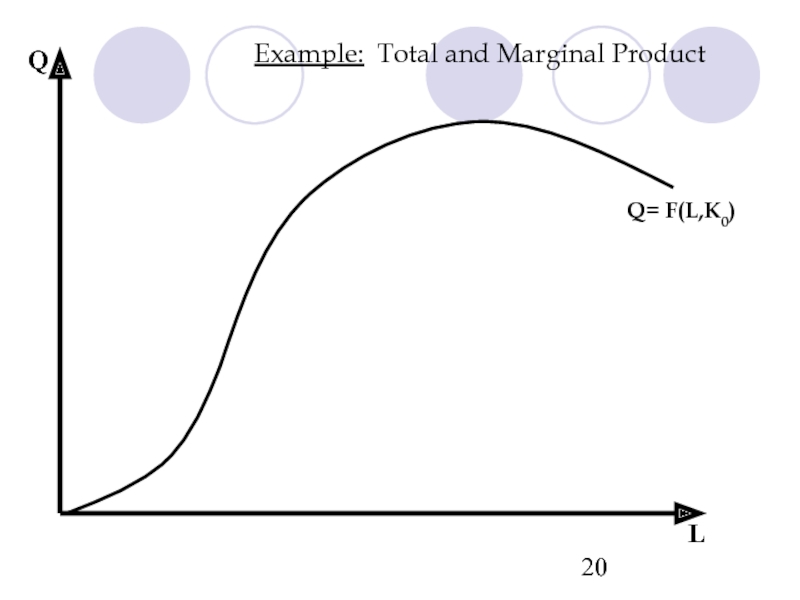
- 20. Q L Q= F(L,K0) Example: Total and Marginal Product
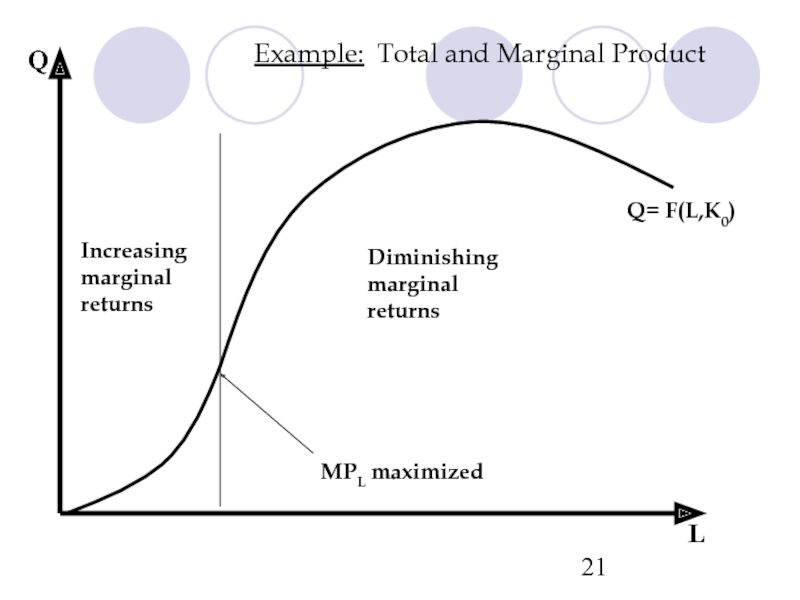
- 21. Q L MPL maximized Q=
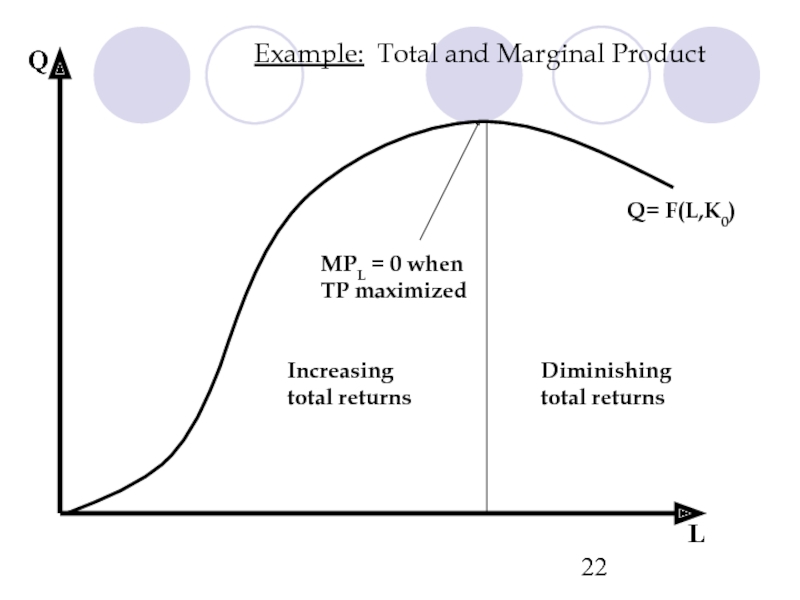
- 22. Q L MPL = 0
- 23. Example: Total and Marginal Product
- 24. Marginal and Average Products There is a
- 25. Marginal and Average Products When marginal product
- 26. Example: Average and Marginal Products L APL MPL MPL maximized APL maximized
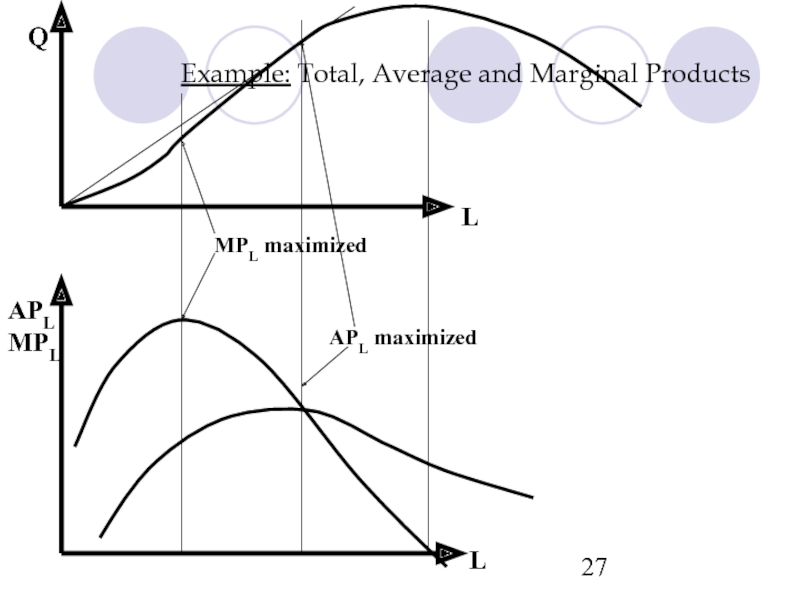
- 27. Example: Total, Average and Marginal Products
- 28. Isoquants Definition: An isoquant is a representation
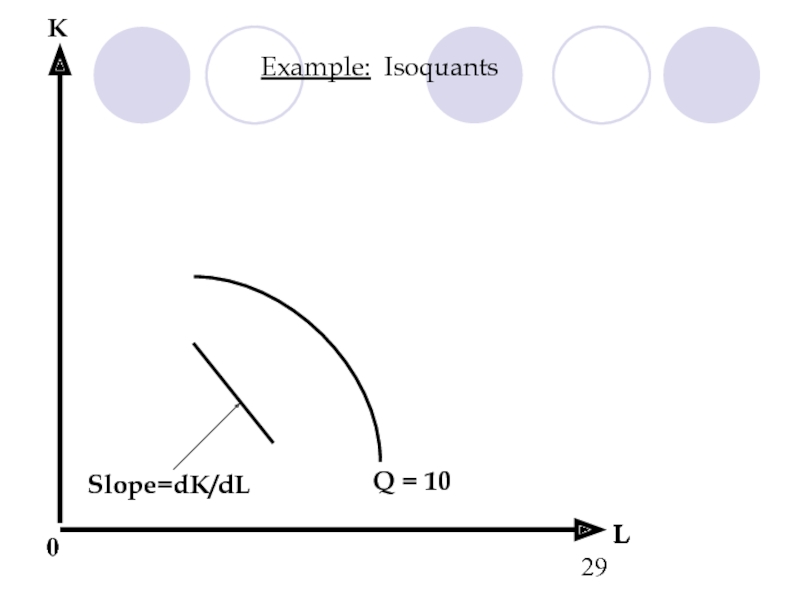
- 29. Example: Isoquants L K Q = 10 0 Slope=dK/dL L
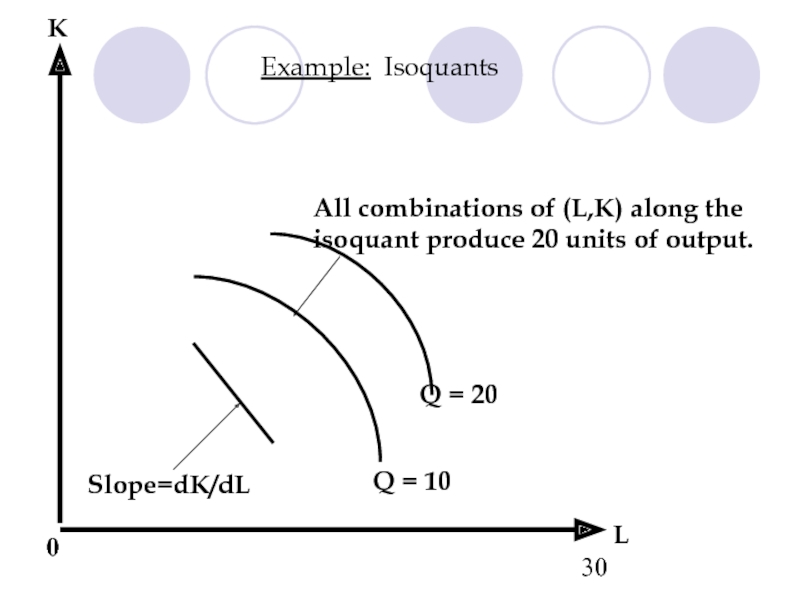
- 30. L Q = 10 Q = 20
- 31. Isoquants Example: Suppose Q = K0.5L0.5
- 32. Definition: The marginal rate of technical substitution
- 33. Marginal Rate Of Technical Substitution Alternative
- 34. Marginal Product and the Marginal Rate
- 35. Marginal Product and the Marginal Rate
- 36. Marginal Product and the Marginal Rate
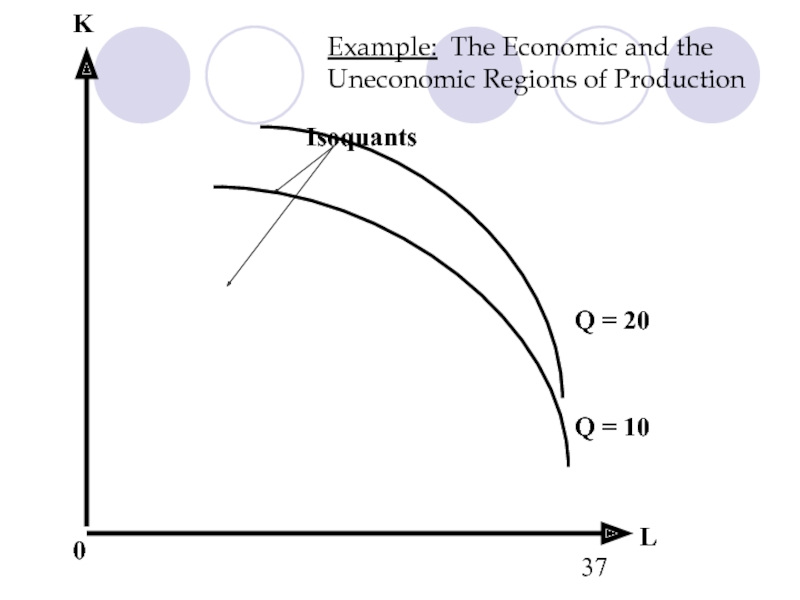
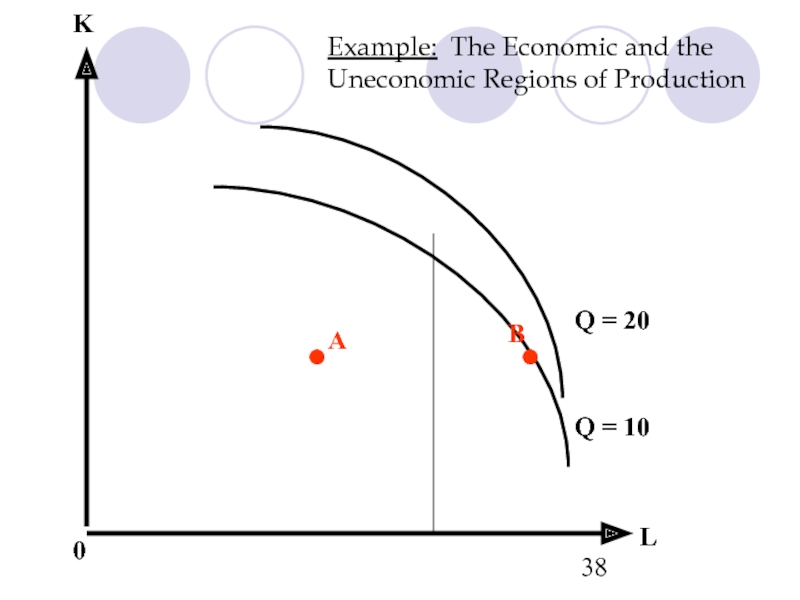
- 37. Example: The Economic and the Uneconomic Regions
- 38. Example: The Economic and the Uneconomic Regions
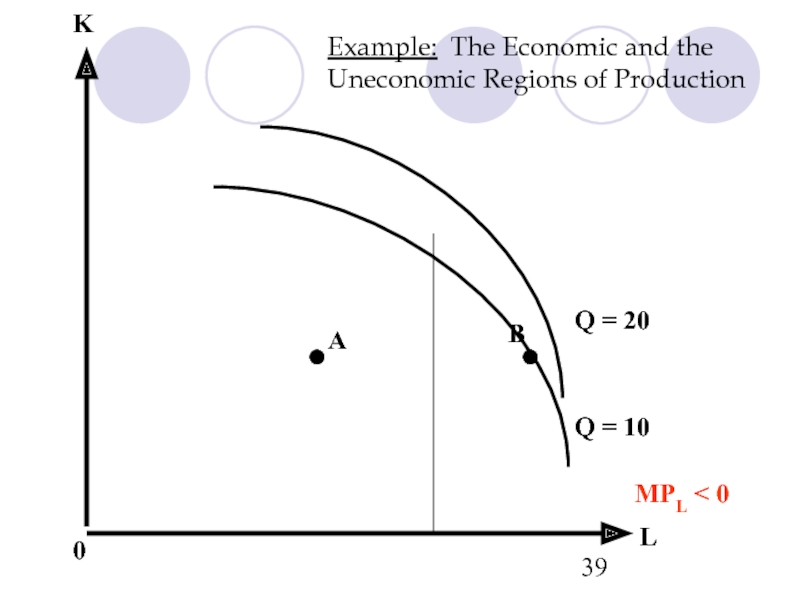
- 39. Example: The Economic and the Uneconomic Regions
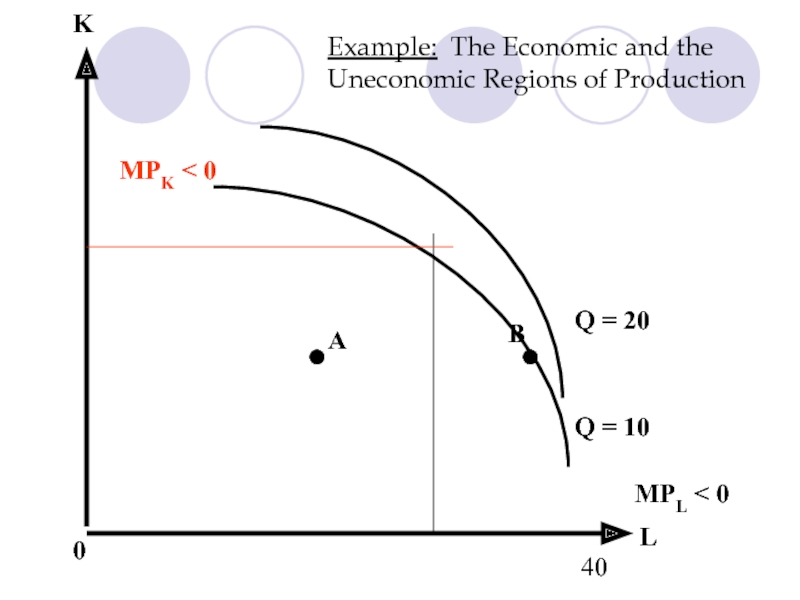
- 40. Example: The Economic and the Uneconomic Regions
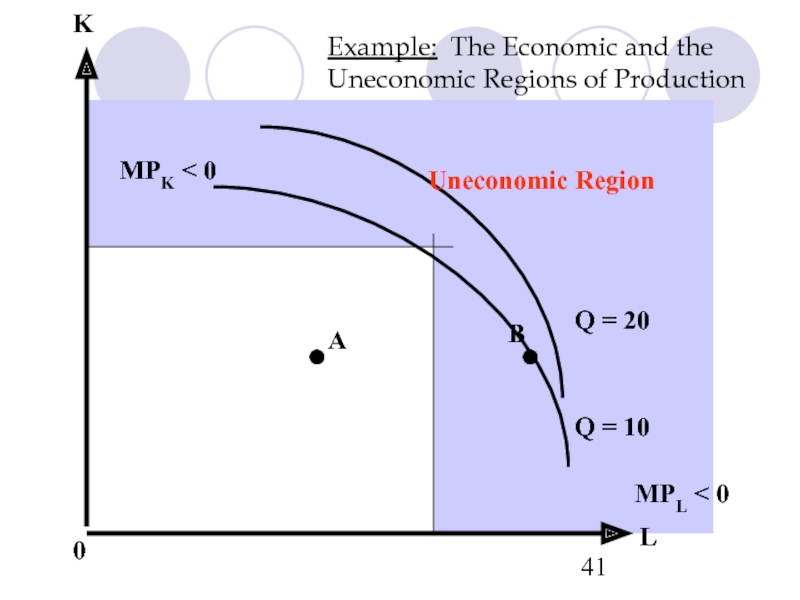
- 41. Example: The Economic and the
- 42. Example: The Economic and
Outline The Production Function Marginal and Average Products Isoquants Marginal Rate of Technical Substitution Returns to Scale Some Special Functional Forms Technological Progress
Слайд 2Outline
The Production Function
Marginal and Average Products
Isoquants
Marginal Rate of Technical Substitution
Returns to
Scale
Some Special Functional Forms
Technological Progress
Some Special Functional Forms
Technological Progress
Слайд 3Definitions
Inputs or factors of production are productive resources that firms use
to manufacture goods and services.
Example: labor, land, capital equipment…
The firm’s output is the amount of goods and services produced by the firm.
Example: labor, land, capital equipment…
The firm’s output is the amount of goods and services produced by the firm.
Слайд 4Definitions
Production transforms a set of inputs into a set of outputs
Technology
determines the quantity of output that is feasible to attain for a given set of inputs.
Слайд 5Definitions
The production function tells us the maximum possible output that can
be attained by the firm for any given quantity of inputs.
Q = F(L,K,T,M,…)
Q = F(L,K,T,M,…)
Слайд 6Definitions
A technically efficient firm is attaining the maximum possible output from
its inputs (using whatever technology is appropriate)
The firm’s production set is the set of all feasible points, including:
The production function (efficient point)
The inefficient points below the production function
The firm’s production set is the set of all feasible points, including:
The production function (efficient point)
The inefficient points below the production function
Слайд 10Example: The Production Function and Technical Efficiency
Q = f(L)
L
Q
•
•
•
•
C
D
A
B
Production Function
Слайд 11
Example: The Production Function and Technical Efficiency
Q = f(L)
L
Q
•
•
•
•
C
D
A
B
Production Set
Production
Function
Слайд 12Notes:
The variables in the production function are flows (amount of input
per unit of time), not stocks (the absolute quantity of the input).
Capital refers to physical capital (goods that are themselves produced goods) and not financial capital (money required to start or maintain production).
Capital refers to physical capital (goods that are themselves produced goods) and not financial capital (money required to start or maintain production).
Слайд 15Marginal Product
Definition: The marginal product of an input is the change
in output that results from a small change in an input
E.g.: MPL = ∂Q MPK = ∂Q
∂L ∂K
It assumes the levels of all other inputs are held constant.
E.g.: MPL = ∂Q MPK = ∂Q
∂L ∂K
It assumes the levels of all other inputs are held constant.
Слайд 16Example: Suppose Q = K0.5L0.5
Then: MPL = ∂Q = 0.5 K0.5
∂L L0.5
MPK = ∂Q = 0.5 L0.5
∂K K0.5
MPK = ∂Q = 0.5 L0.5
∂K K0.5
Marginal Product
Слайд 17Average Product
Definition: The average product of an input is equal to
the total output to be produced divided by the quantity of the input that is used in its production
E.g.: APL = Q APK = Q
L K
E.g.: APL = Q APK = Q
L K
Слайд 18Example: Suppose Q = K0.5L0.5
Then: APL = Q = K0.5L0.5 =
K0.5
L L L0.5
APK = Q = K0.5L0.5 = L0.5
K K K0.5
L L L0.5
APK = Q = K0.5L0.5 = L0.5
K K K0.5
Average Product
Слайд 19Law of Diminishing Marginal Returns
Definition: The law of diminishing marginal returns
states that the marginal product (eventually) declines as the quantity used of a single input increases.
Слайд 21Q
L
MPL maximized
Q= F(L,K0)
Example: Total and Marginal Product
Increasing marginal returns
Diminishing marginal returns
Слайд 22Q
L
MPL = 0 when
TP maximized
Q= F(L,K0)
Example: Total and Marginal Product
Diminishing total
returns
Increasing total returns
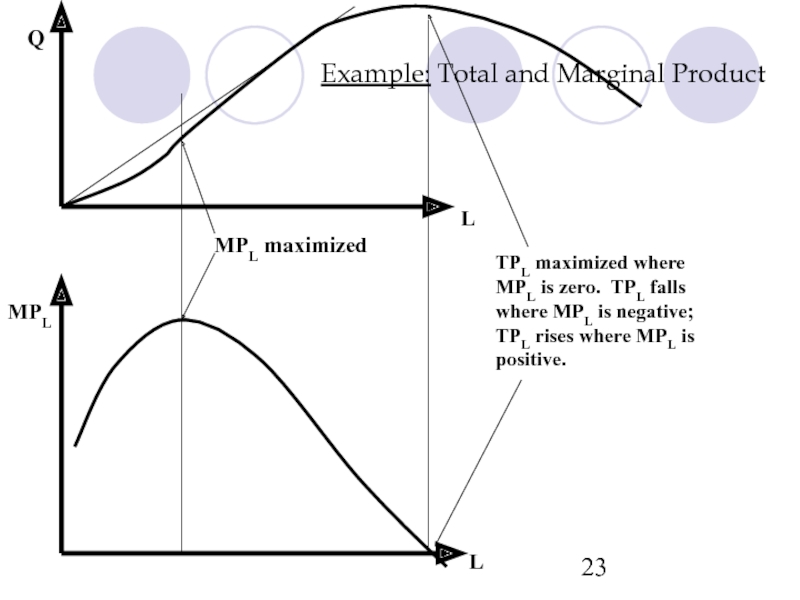
Слайд 23Example: Total and Marginal Product
L
MPL
Q
L
MPL maximized
TPL maximized where
MPL is zero. TPL
falls
where MPL is negative;
TPL rises where MPL is
positive.
where MPL is negative;
TPL rises where MPL is
positive.
Слайд 24Marginal and Average Products
There is a systematic relationship between average product
and marginal product.
This relationship holds for any comparison between any marginal magnitude with the average magnitude.
This relationship holds for any comparison between any marginal magnitude with the average magnitude.
Слайд 25Marginal and Average Products
When marginal product is greater than average product,
average product is increasing.
E.g., if MPL > APL , APL increases in L.
When marginal product is less than average product, average product is decreasing.
E.g., if MPL < APL, APL decreases in L.
E.g., if MPL > APL , APL increases in L.
When marginal product is less than average product, average product is decreasing.
E.g., if MPL < APL, APL decreases in L.
Слайд 28Isoquants
Definition: An isoquant is a representation of all the combinations of
inputs (labor and capital) that allow that firm to produce a given quantity of output.
Слайд 30L
Q = 10
Q = 20
All combinations of (L,K) along the
isoquant produce
20 units of output.
0
Slope=dK/dL
K
Example: Isoquants
Слайд 31Isoquants
Example: Suppose Q = K0.5L0.5
For Q = 20 => 20 =
K0.5L0.5
=> 400 = KL
=> K = 400/L
For Q = Q0 => K = (Q0)2 /L
=> 400 = KL
=> K = 400/L
For Q = Q0 => K = (Q0)2 /L
Слайд 32Definition: The marginal rate of technical substitution measures the rate at
which the firm can substitute a little more of an input for a little less of another input, in order to produce the same output as before.
Marginal Rate Of Technical Substitution
Слайд 33Marginal Rate Of Technical Substitution
Alternative Definition : It is the
negative of the slope of the isoquant:
MRTSL,K = — dK (for a constant level of
dL output)
MRTSL,K = — dK (for a constant level of
dL output)
Слайд 34Marginal Product and the Marginal
Rate of Technical Substitution
We can
express the MRTS as a ratio of the marginal products of the inputs in that basket
Using differentials, along a particular isoquant:
MPL . dL + MPK . dK = dQ = 0
Solving:
MPL = _ dK = MRTSL,K
MPK dL
Using differentials, along a particular isoquant:
MPL . dL + MPK . dK = dQ = 0
Solving:
MPL = _ dK = MRTSL,K
MPK dL
Слайд 35Marginal Product and the Marginal
Rate of Technical Substitution
Notes:
If we
have diminishing marginal returns, we also have a diminishing marginal rate of technical substitution.
In other words, the marginal rate of technical substitution of labour for capital diminishes as the quantity of labour increases along an isoquant.
In other words, the marginal rate of technical substitution of labour for capital diminishes as the quantity of labour increases along an isoquant.
Слайд 36Marginal Product and the Marginal
Rate of Technical Substitution
Notes:
If both
marginal products are positive, the slope of the isoquant is negative
For many production functions, marginal products eventually become negative. Then:
MRTS < 0
We reach an uneconomic region of production
For many production functions, marginal products eventually become negative. Then:
MRTS < 0
We reach an uneconomic region of production
Слайд 40Example: The Economic and the Uneconomic Regions of Production
L
K
Q =
10
Q = 20
0
MPK < 0
MPL < 0
•
•
B
A
Слайд 41
Example: The Economic and the Uneconomic Regions of Production
L
K
Q =
10
Q = 20
0
MPK < 0
MPL < 0
•
•
B
A
Uneconomic Region
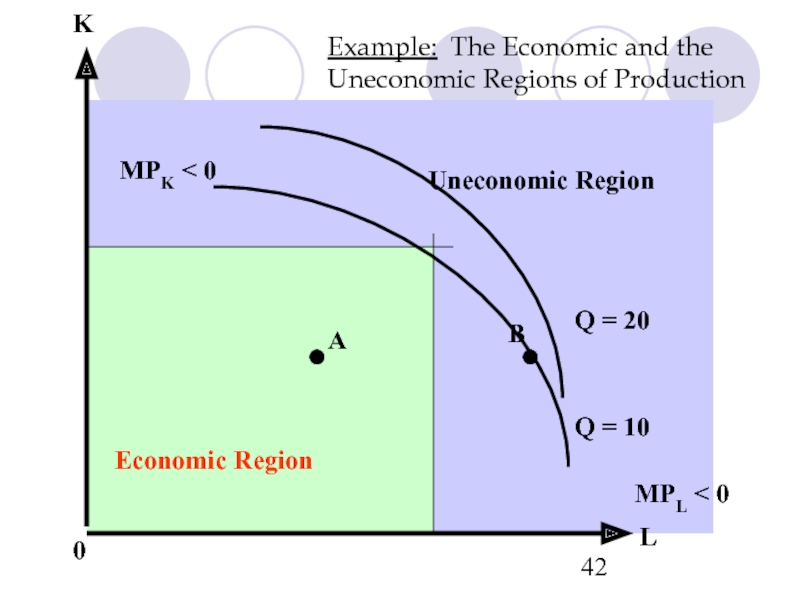
Слайд 42
Example: The Economic and the Uneconomic Regions of Production
L
K
Q =
10
Q = 20
0
MPK < 0
MPL < 0
•
•
B
A
Uneconomic Region
Economic Region
