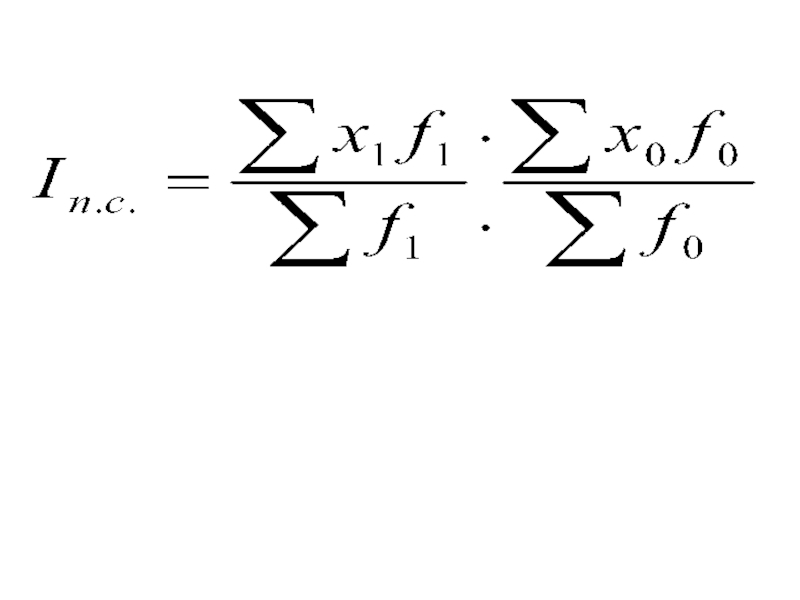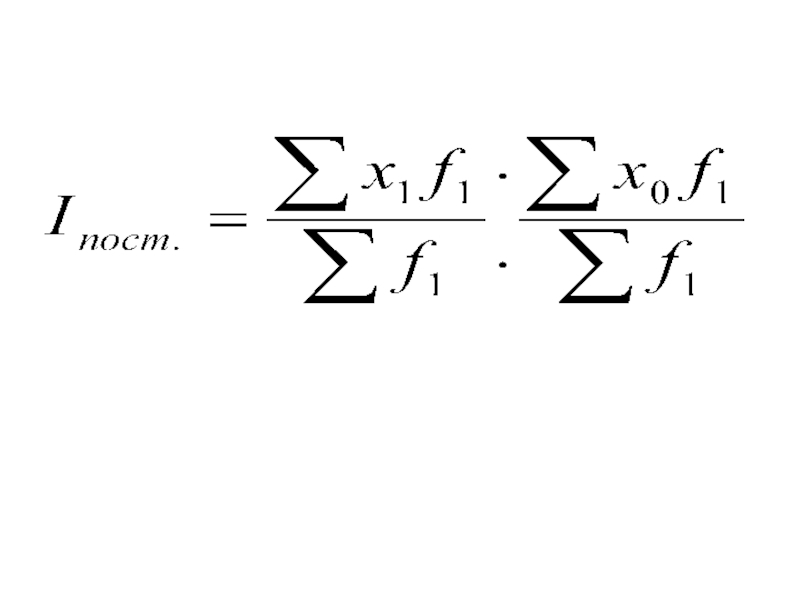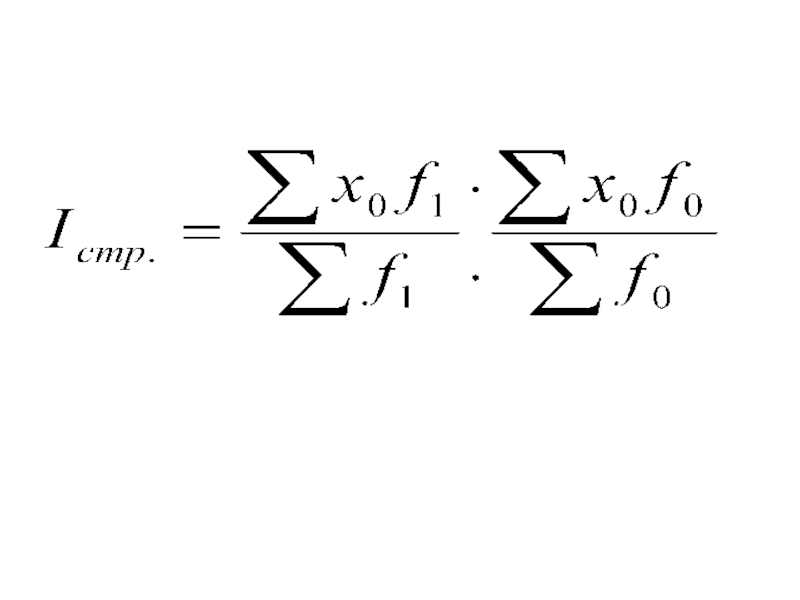объёма или уровня явлений в отчётном периоде по сравнению с базисным.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Индексы презентация
Содержание
- 1. Индексы
- 2. условные обозначения: i - индивидуальный индекс; I
- 3. индивидуальные индексы индивидуальный индекс цен индивидуальный индекс физического объёма индивидуальный индекс стоимости
- 4. Агрегатные индексы физического объёма, цен и
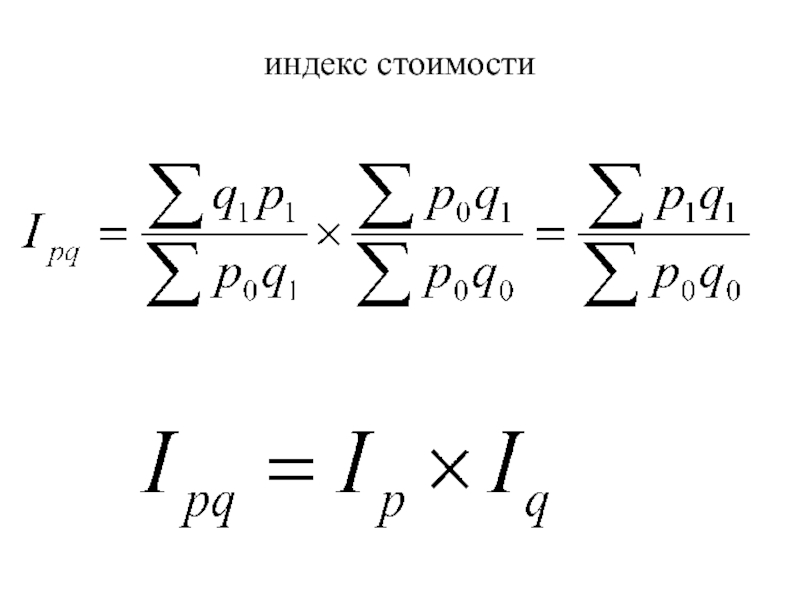
- 5. индекс стоимости
- 6. Формулы агрегатных индексов позволяют разложить общий абсолютный прирост стоимости по факторам
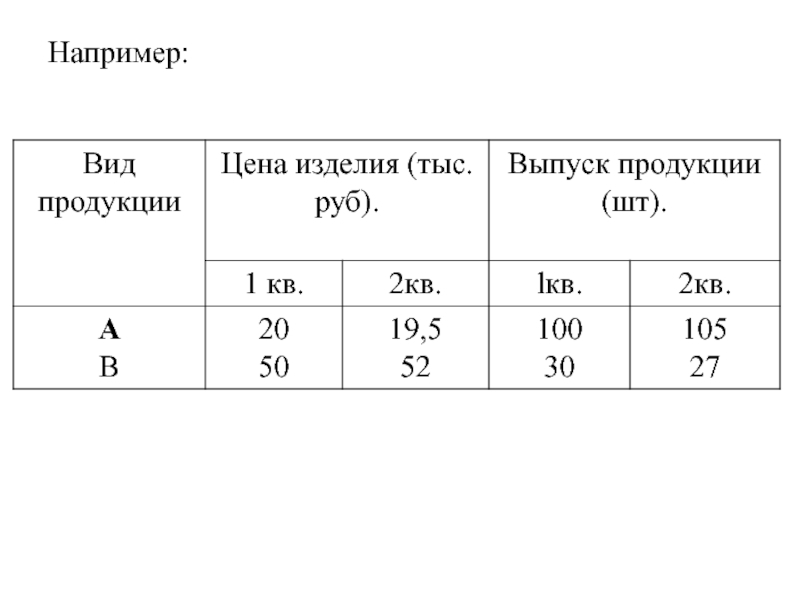
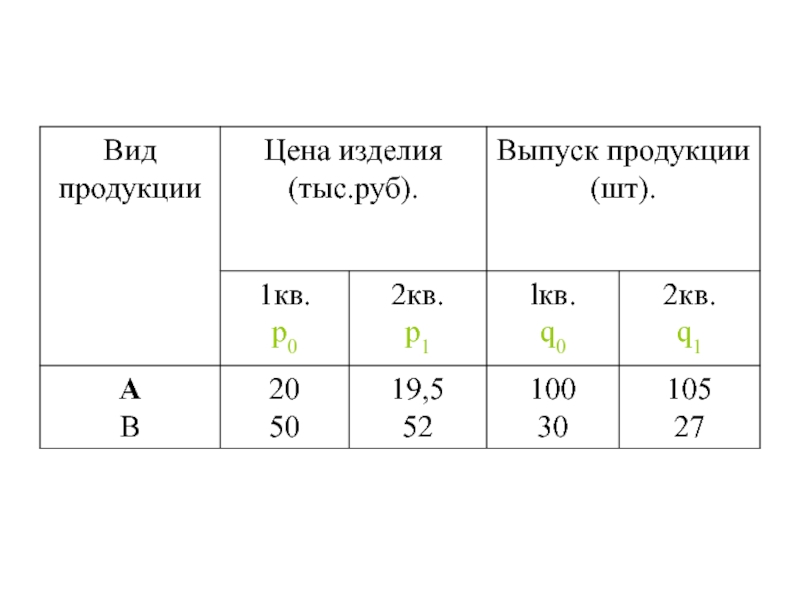
- 7. Например:
- 9. Решение 1. Определим общий индекс стоимости: Таким
- 10. 2. Определим общий индекс цены: Таким образом, общий
- 11. 3. Определим общий индекс физического объёма: Таким образом,
- 12. индексы себестоимости Индивидуальный индекс себестоимости характеризует изменение себестоимости отдельных видов продукции
- 13. Сводный индекс себестоимости рассчитывается для определения себестоимости
- 14. показывает сумму экономии предприятия от снижения себестоимости.
- 15. Сводный индекс физического объема, взвешенный по себестоимости
- 16. Сводный индекс затрат на производство
- 17. Средние арифметические и средние гармонические индексы На
- 18. Средний арифметический индекс физического объема
- 19. Рассмотрим вывод: т.к.
- 20. средний гармонический индекс физического объёма
- 21. Для индексов цены вывод аналогичен средний
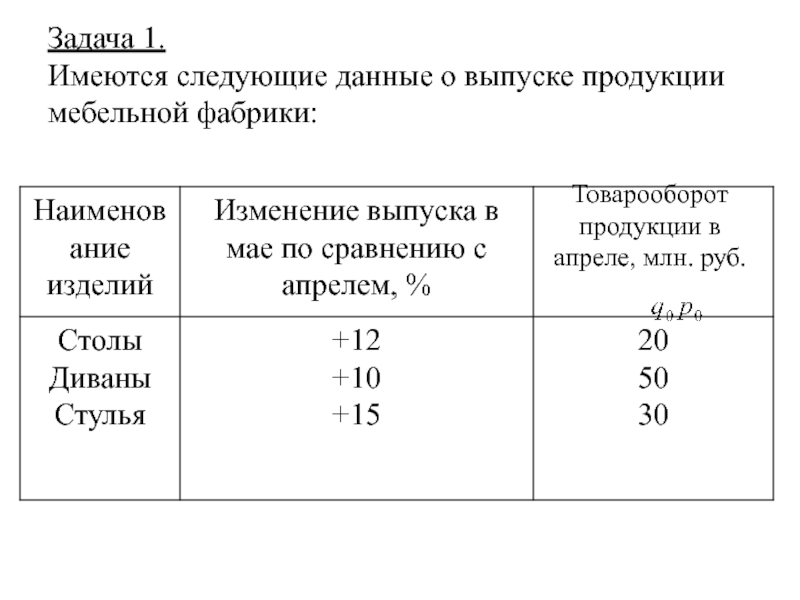
- 22. Задача 1. Имеются следующие данные о
- 23. Определить увеличение выпуска всей продукции в мае
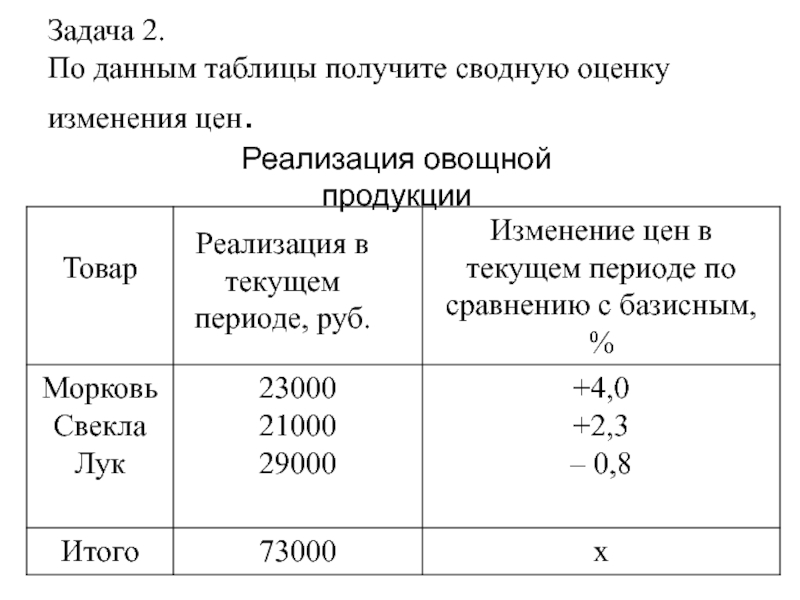
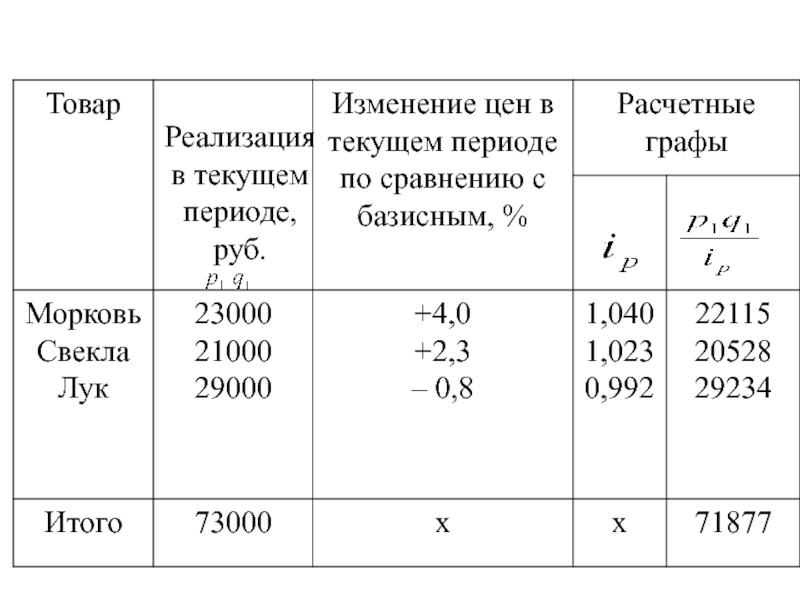
- 24. Задача 2. По данным таблицы получите
- 25. Реализация в текущем периоде, руб.
- 26. Решение Вычислим средний гармонический индекс цен:
- 27. Базисные и цепные индексы, их взаимосвязь
- 28. Для индивидуальных индексов цен, физического объёма и
- 29. 2. Отношение базисного индекса отчётного периода к базисному
- 30. Задача 3. Имеются следующие данные об
- 31. Определить на сколько процентов увеличилось число рабочих
- 32. Индексы средних величин 1. Индекс переменного состава
- 34. 2. Индекс постоянного состава 2. Индекс постоянного
- 36. 3. Индекс рассчитанных по типу индекс
- 38. Взаимосвязь:
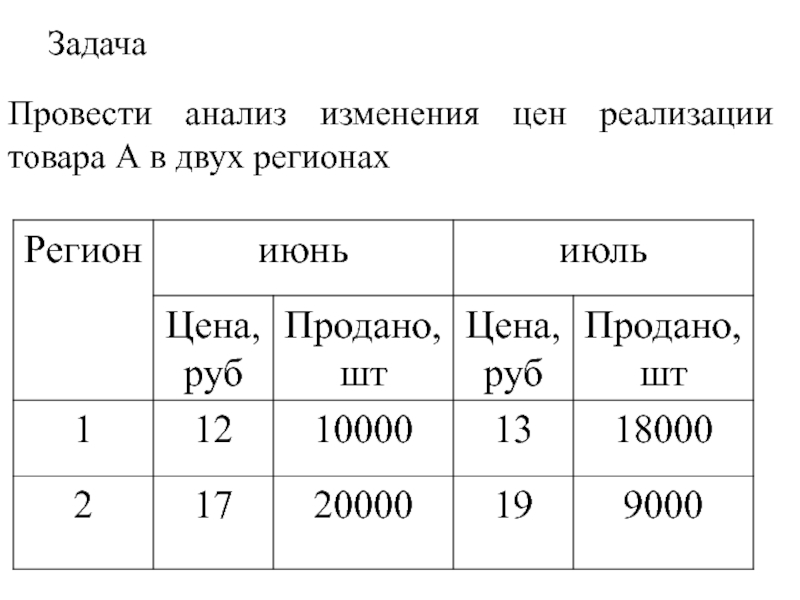
- 39. Задача Провести анализ изменения цен реализации товара А в двух регионах
- 40. 1. Вычислить индексы переменного, постоянного
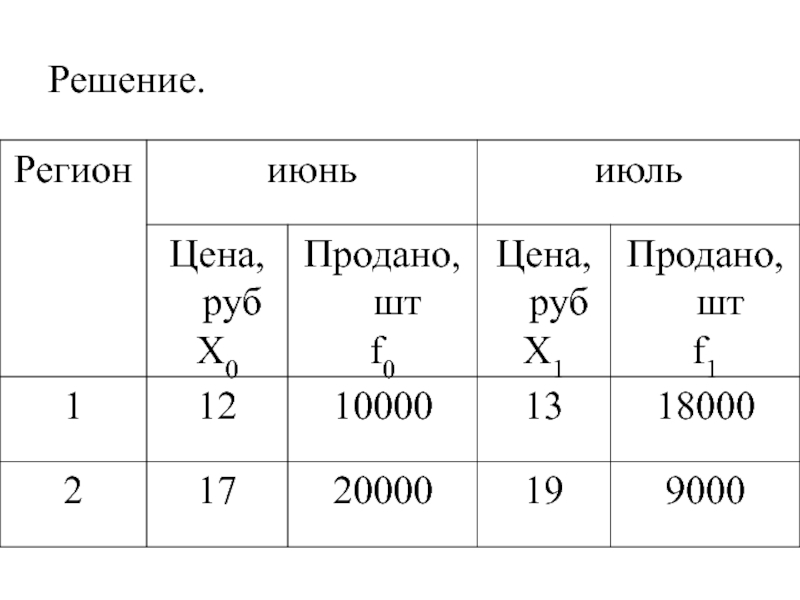
- 41. Решение.
- 42. 1. Вычислим индекс переменного состава или 97,8%
- 43. 2. Вычислим индекс постоянного состава или 109,7%
- 44. 3. Вычислим индекс структурных сдвигов или 89,17%
- 45. Проверим взаимосвязь вычисленных индексов: 0,978=1,097 х 0,8917 (верно)
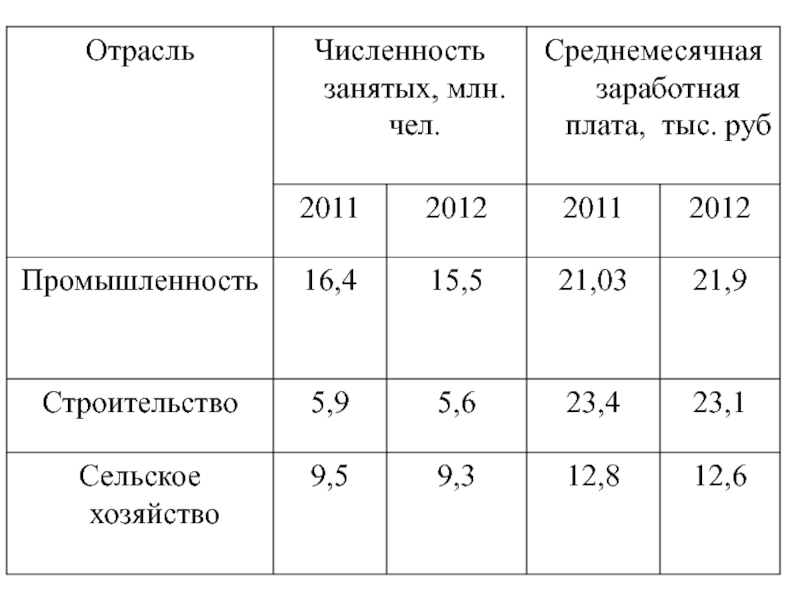
- 46. Задача 2: Имеются следующие данные за
- 48. Вычислить индексы переменного, постоянного состава и
- 50. 1. Вычислим индекс переменного состава Или 101,42%
- 51. 2. Вычислим индекс постоянного состава Или 101,7%
- 52. 3. Вычислим индекс структурных сдвигов Или 99,68%
- 53. Проверим взаимосвязь вычисленных индексов: 1,0142=1,017 х 0,9968 (верно)
условные обозначения: i - индивидуальный индекс; I - общий индекс; р - цена единицы продукции; q - объём выпуска продукции.
Слайд 1ИНДЕКСЫ
Индекс - это относительный показатель динамики общественных явлений, который характеризует изменение
Слайд 2условные обозначения:
i - индивидуальный индекс;
I - общий индекс;
р - цена
единицы продукции;
q - объём выпуска продукции.
Слайд 3индивидуальные индексы
индивидуальный индекс цен
индивидуальный индекс физического объёма
индивидуальный индекс стоимости
Слайд 4 Агрегатные индексы физического объёма, цен и себестоимости
агрегатный (общий) индекс
физического объёма (индекс количественного показателя)
агрегатный (общий) индекс цен (индекс качественного показателя)
Слайд 6Формулы агрегатных индексов позволяют разложить общий абсолютный прирост стоимости по факторам
Слайд 9Решение
1. Определим общий индекс стоимости:
Таким образом стоимость продукции уменьшилась на 1,39%,
а экономический эффект составил 48,5 тыс.руб.
Слайд 102. Определим общий индекс цены:
Таким образом, общий индекс цены возрос на 0,04%,
а абсолютный прирост стоимости, вызванный увеличением цен равен 1,5 тыс. руб.
Слайд 113. Определим общий индекс физического объёма:
Таким образом, на 1,43% стоимость снизилась из-за
уменьшения выпуска продукции, что в абсолютном выражении равно 50 тыс. руб.
Слайд 12индексы себестоимости
Индивидуальный индекс себестоимости
характеризует изменение себестоимости отдельных видов продукции
Слайд 13Сводный индекс себестоимости рассчитывается для определения себестоимости нескольких видов продукции, выпускаемых
предприятием.
При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода.
При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода.
Слайд 17Средние арифметические и средние гармонические индексы
На практике очень часто не известны
абсолютные значения индексируемых величин, а имеются данные об их относительном изменении. В таких случаях вместо агрегатных индексов вычисляются средние из индивидуальных индексов, которые в свою очередь делятся на:
- средние арифметические
- средние гармонические
Применение той или иной формулы индекса зависит от имеющейся в нашем распоряжении информации
- средние арифметические
- средние гармонические
Применение той или иной формулы индекса зависит от имеющейся в нашем распоряжении информации
Слайд 21Для индексов цены вывод аналогичен
средний арифметический индекс цены
средний гармонический
индекс цены
Слайд 22Задача 1.
Имеются следующие данные о выпуске продукции мебельной фабрики:
Товарооборот продукции
в апреле, млн. руб.
Слайд 23Определить увеличение выпуска всей продукции в мае по сравнению с апрелем
(в %), т.е. рассчитать общий индекс физического объема.
Решение.
Общий индекс физического объема может быть рассчитан как средний арифметический:
или 111,9%
Слайд 24Задача 2.
По данным таблицы получите сводную оценку изменения цен.
Реализация овощной
продукции
Реализация в текущем периоде, руб.
Слайд 26Решение
Вычислим средний гармонический индекс цен:
или 101,6%.
Таким образом, цены по данной
товарной группе в текущем периоде по сравнению с базисным периодом, в среднем выросли на 1,6%.
Слайд 27Базисные и цепные индексы, их взаимосвязь
Так как индексы являются относительной
величиной динамики, то они также могут быть базисными и цепными:
– базисные индексы получают сопоставлением с уровнем периода, принятого за базу сравнения, т.е. база сравнения, остаётся постоянной;
– цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
– базисные индексы получают сопоставлением с уровнем периода, принятого за базу сравнения, т.е. база сравнения, остаётся постоянной;
– цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
Слайд 28Для индивидуальных индексов цен, физического объёма и стоимости продукции справедливо следующие
правила:
1. Последовательное произведение цепных индексов даёт базисный индекс последнего периода:
или
Слайд 292. Отношение базисного индекса отчётного периода к базисному индексу предшествующего периода даёт
цепной индекс отчётного периода
или
Слайд 30Задача 3.
Имеются следующие данные об изменении численности рабочих на заводе,
в % к предыдущему году:
Слайд 31Определить на сколько процентов увеличилось число рабочих на заводе за 5
лет, т.е. в 2011 году по сравнению с 2006 годом.
Решение.
Зная, что базисный индекс можно получить путем перемножения цепных индексов, находим:
(или 130%), т.е. за 5 лет число рабочих на заводе возросло на 30%.
Слайд 32Индексы средних величин
1. Индекс переменного состава -
- отношение 2-х средних величин – учитывает
одновременно и структурные изменения в составе совокупности и изменение уровня качественного признака у отдельных объектов. Если индексируемую величину обозначить через х, а веса через f , то в общем виде индекс переменного состава можно записать в виде:
Индекс переменного состава -
-
Слайд 342. Индекс постоянного состава
2. Индекс постоянного состава
- вычисляется
по типу индекса цены. Если при расчете средних величин за два периода зафиксировать веса одного и того же периода, то при сравнении таких средних величин индекс постоянного (или фиксированного) состава:
2. Индекс постоянного состава
Слайд 363. Индекс рассчитанных по типу
индекс структурных изменений (сдвигов) -
- показывает, во
сколько раз изменился общий средний уровень за счёт изменения удельного веса каждого объекта в общем объёме признака. При сравнении средних показателей принимают неизменными значения х, тогда на динамику изменения средних будет оказывать влияние только изменение весов.
Слайд 401. Вычислить индексы переменного,
постоянного
состава и структурных сдвигов.
2. Проверить
взаимосвязь вычисленных
индексов
индексов
Слайд 46Задача 2:
Имеются следующие данные за 2011 и
2012 гг. о средней
заработной плате
и численности занятых в трех отраслях
экономики РФ:
и численности занятых в трех отраслях
экономики РФ:
Слайд 48Вычислить индексы переменного, постоянного
состава и структурных сдвигов средней
заработной платы.
Проверить взаимосвязь
вычисленных индексов
Решение.
вычисленных индексов
Решение.
