- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ekonomie 1 Bakaláři První cvičení Základní pojmy, zákony a principy ekonomie презентация
Содержание
- 1. Ekonomie 1 Bakaláři První cvičení Základní pojmy, zákony a principy ekonomie
- 2. Povinná literatura:
- 3. Co je hlavní příčinou vzniku ekonomické vědy?
- 4. Co je hlavní příčinou vzniku ekonomické vědy? Nutnost optimalizovat využití vzácných zdrojů!
- 5. Klasická ekonomie se zabývá: nabídkovou stranou
- 6. Klasická ekonomie se zabývá: nabídkovou stranou
- 7. Jaká ekonomická věda se zabývá poptávkovou stranu trhu?
- 8. Jaká ekonomická věda se zabývá poptávkovou stranu trhu? Marginalistická ekonomie jako část neoklasické ekonomie.
- 9. Jak se liší mikroekonomie od makroekonomie?
- 10. Jak se liší mikroekonomie od makroekonomie? Základními subjekty jsou: podnikatelé, spotřebitelé státy, národní ekonomika
- 11. Definujte ekonomii!
- 12. Vymezení ekonomie „Ekonomie je věda
- 13. Co je to makroekonomie?
- 14. Makroekonomie je věda zkoumající komplexní účinky chování
- 15. Jakou formu má kapitál?
- 16. peníze půda, budovy stroje zařízení, nástroje lidé
- 17. Z čeho plyne omezenost a tím i vzácnost výrobních faktorů?
- 18. Z čeho plyne omezenost a tím i
- 19. Jaké jsou klíčové otázky praktické ekonomie?
- 20. CO ? Jak ? Kolik ? Za kolik ?
- 21. Jakou ztrátu oproti nákladům obětované příležitosti utrpíte pokud vykonáváte optimální povolání?
- 22. Princip nákladů obětované příležitosti
- 23. Jaké povolání je nejvhodnější?
- 24. Jaké povolání je nejvhodnější? Kde nejvíc vyděláte.
- 25. Jaké povolání je nejvhodnější? Kde nejvíc vyděláte.
- 26. Je někdo schopen uspokojit všechny své potřeby osobně?
- 27. Je někdo schopen uspokojit všechny své potřeby
- 28. Je někdo schopen uspokojit všechny své potřeby
- 29. Otázky a příklady kap.1, str.34
- 30. Otázky a příklady kap.1, str.34 Student VŠ
- 31. Jak souvisí vymezení ekonomického zisku a efektivnosti na úrovni podniku?
- 32. Efektivnost Pro podnikatele je výstupem celkový
- 33. Může se při stálé efektivnosti rozšiřovat produkce
- 34. Může se při stálé efektivnosti rozšiřovat produkce
- 35. Co se mění při čistě extenzivním vývoji, zisk nebo efektivnost?
- 36. Změnila se efektivnost? Př. 14/1.kap.
- 37. Změnila se efektivnost? Př. 14/1.kap.
- 38. Změnila se efektivnost? Př. 14/1.kap. TR TR=4 TC=2 EP=2 TR=8 TC=4 EP=4 TR=8 TC=2 EP=6
- 39. Ekonomický zisk (EP) dostaneme tak, že od
- 40. Ekonomický zisk (EP) dostaneme tak, že od
- 41. Co je to synergický efekt?
- 42. Každý obchod by měl být paretovsky efektivní!! Podstatou této efektivnosti je synergický efekt!!
- 43. Podstatou této optimalizace je synergický efekt!! ?
- 44. Podstatou této efektivnosti je synergický efekt!!
- 45. Numerický příklad na synergický efekt: Optimálně
- 46. Numerický příklad na synergický efekt: Optimálně
- 47. Co je hlavním zdrojem ekonomické optimalizace?
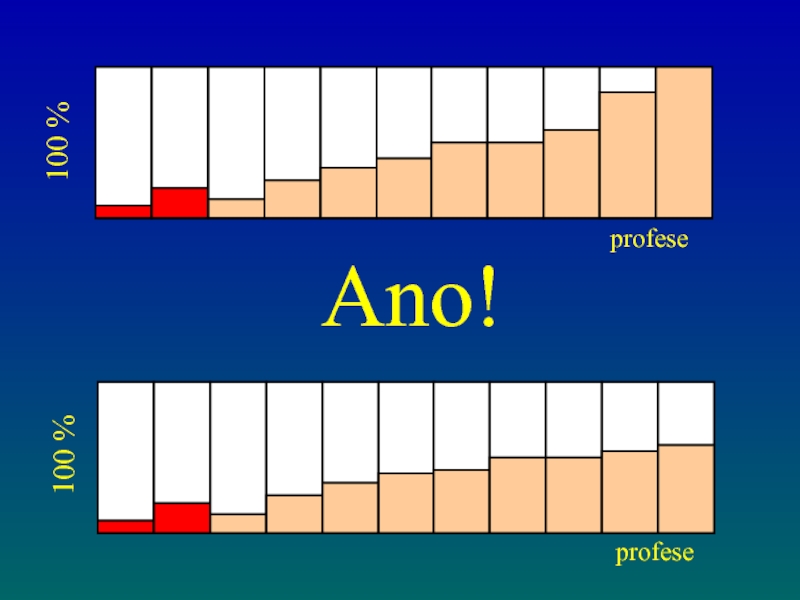
- 48. Synergický efekt! 100 % 100 % profese profese
- 49. Má každý člověk nějaké optimální povolání?
- 50. Ano! 100 % 100 % profese profese
- 51. Co je to zlaté pravidlo podnikatele?
- 52. Zlaté pravidlo podnikatele MR ≥ MC
- 53. Rovnováha firmy nastává tam, kde se protínají
- 54. Rovnováha firmy nastává tam, kde se protínají
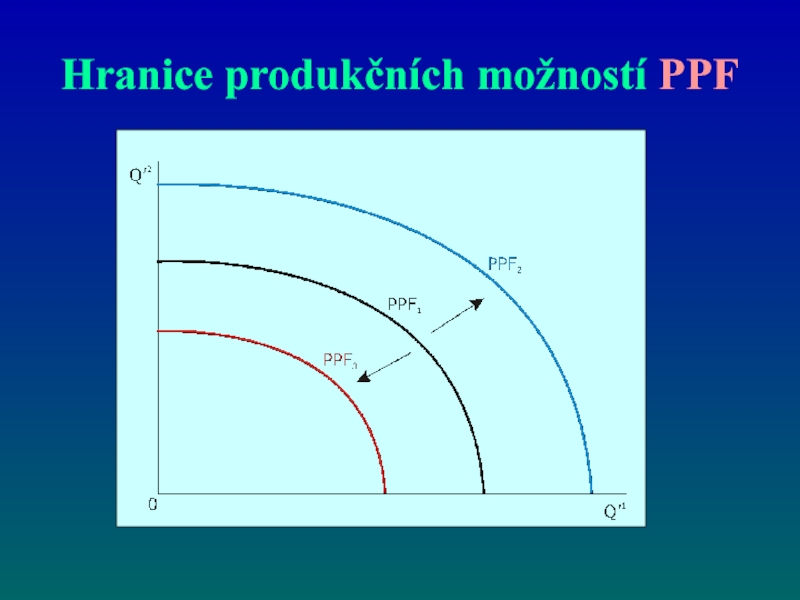
- 55. Co je to hranice produkčních možností PPF?
- 56. Hranice produkčních možností PPF
- 57. Hranice produkčních možností PPF
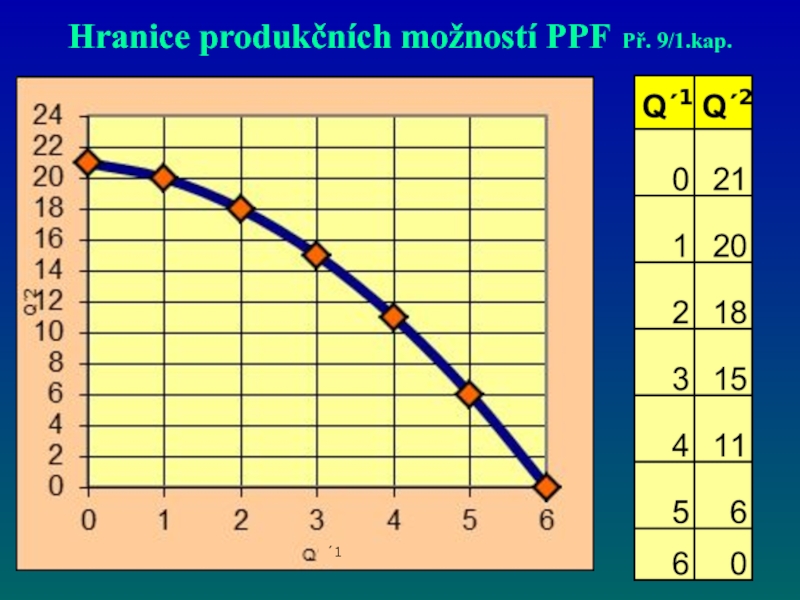
- 58. Otázky a příklady kap.1, str.34; př. 9
- 59. Hranice produkčních možností PPF Př. 9/1.kap. ´1
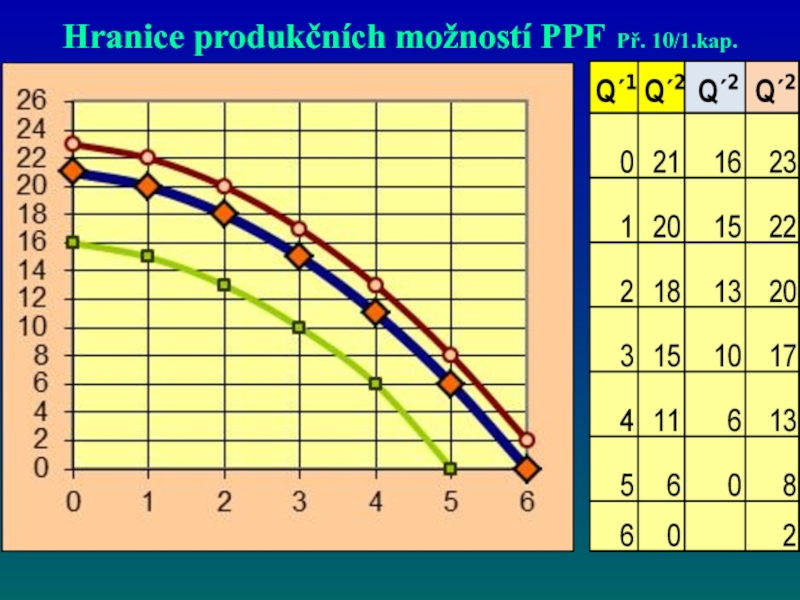
- 60. Otázky a příklady kap.1, str.34; př. 10
- 61. Hranice produkčních možností PPF Př. 10/1.kap.
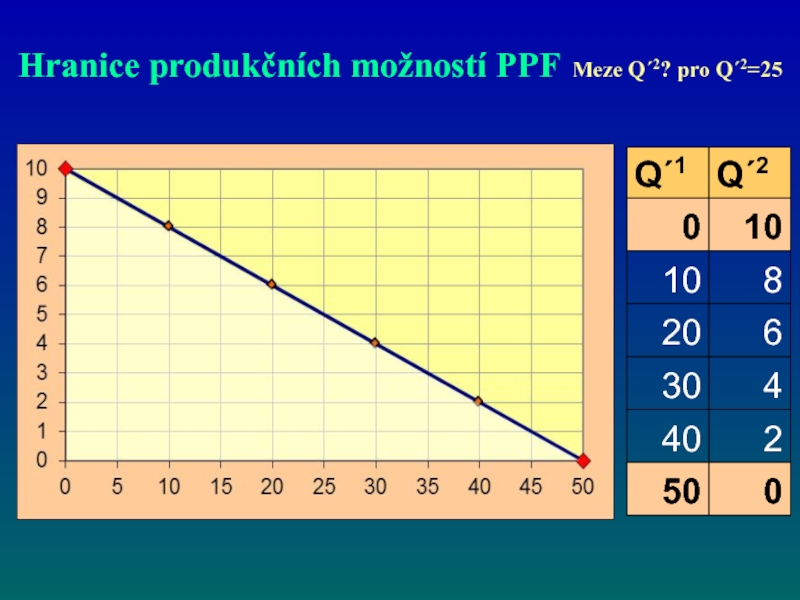
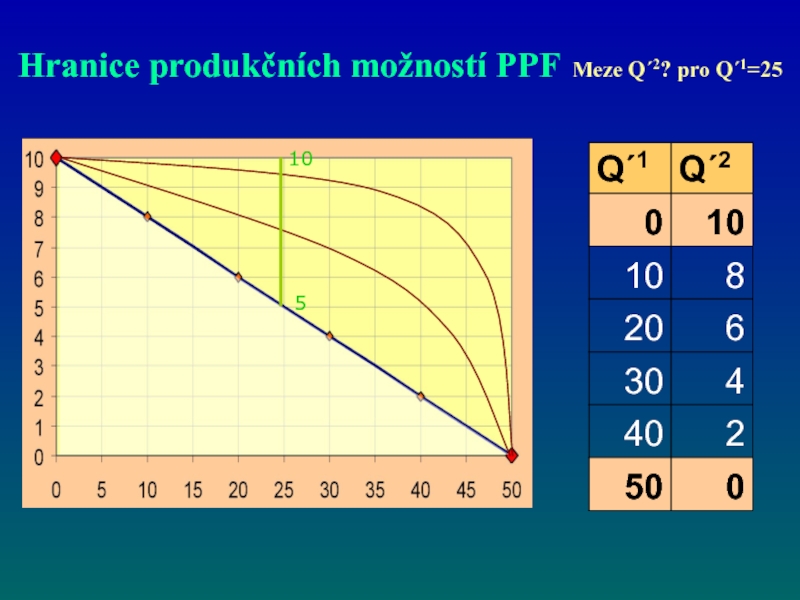
- 62. Hranice produkčních možností PPF Meze Q´2? pro
- 63. Hranice produkčních možností PPF Meze Q´2? pro Q´2=25
- 64. Hranice produkčních možností PPF Meze Q´2? pro Q´1=25 10 5
- 65. Co je to produkční funkce?
- 66. Je to funkční vztah mezi vstupy (nezávisle proměnná) a výstupy (závisle proměnná)
- 67. Otázky a příklady kap.1, str.34; př.24 Na
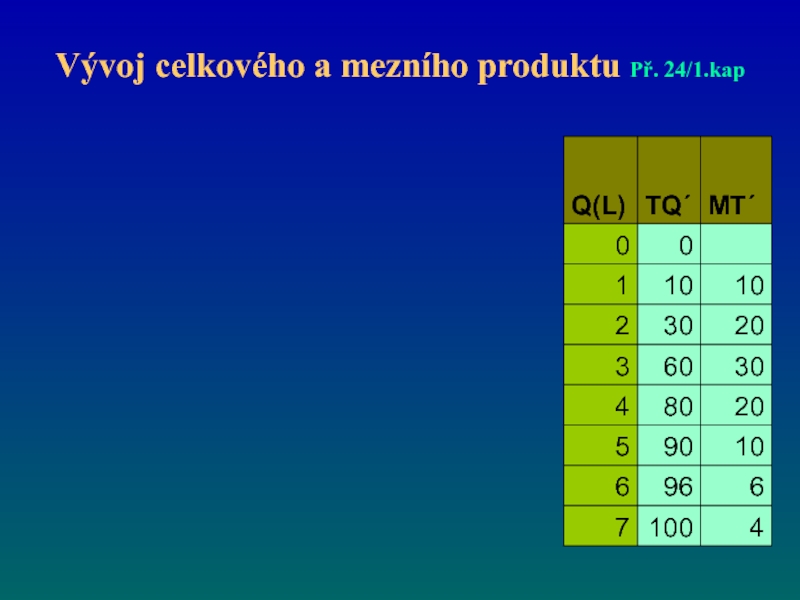
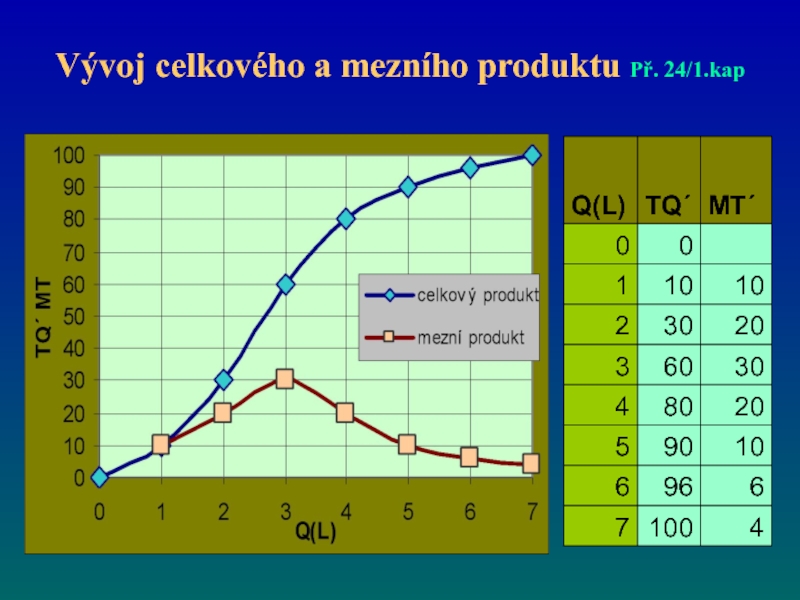
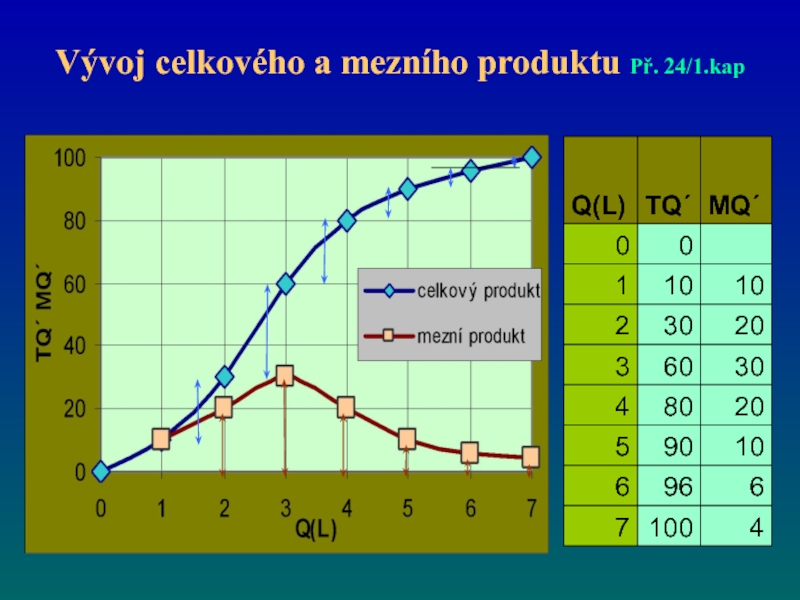
- 68. Vývoj celkového a mezního produktu Př. 24/1.kap
- 69. Vývoj celkového a mezního produktu Př. 24/1.kap
- 70. Vývoj celkového a mezního produktu Př. 24/1.kap
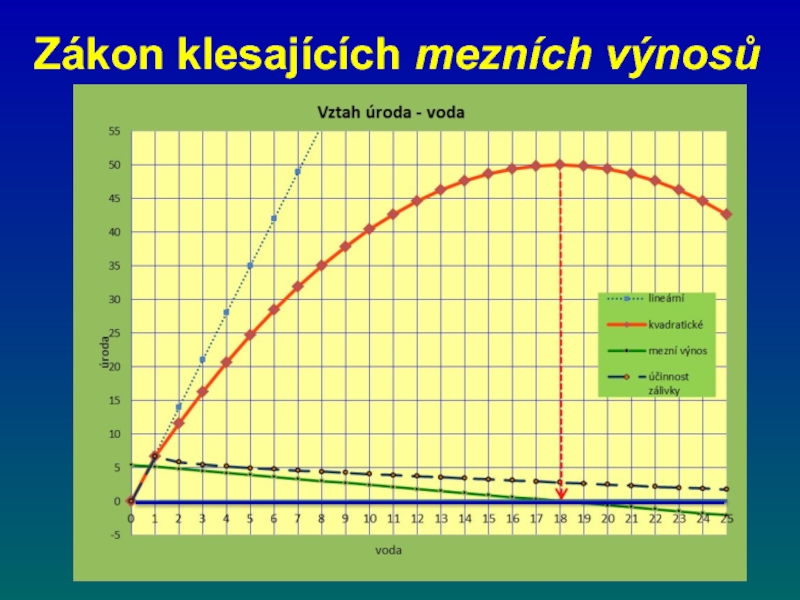
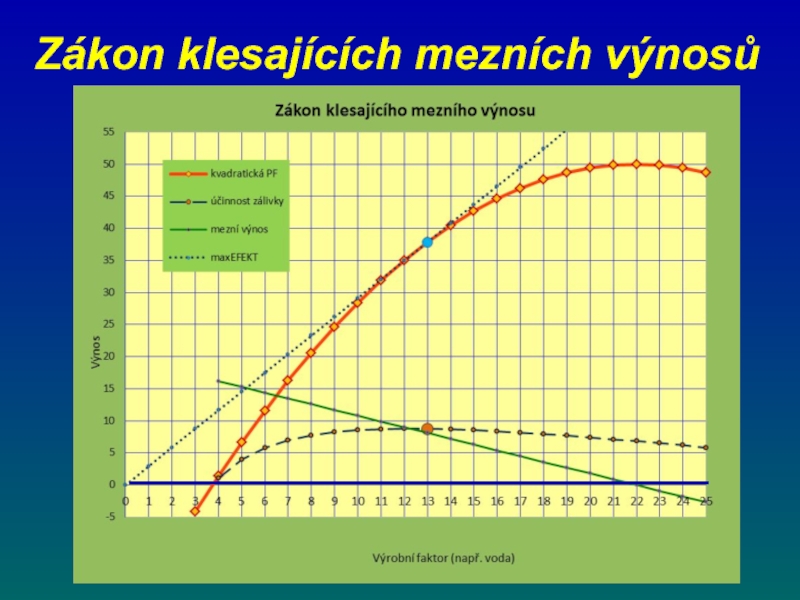
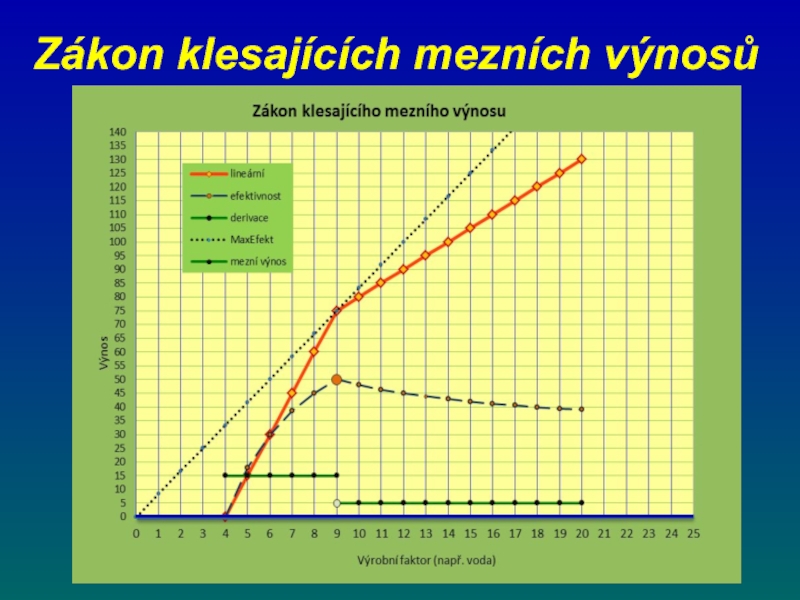
- 71. Zákon klesajících mezních výnosů
- 72. Zákon klesajících mezních výnosů
- 73. Zákon klesajících mezních výnosů
- 74. Marie si koupila nový deštník, ale zapomněla
- 75. Marie si koupila nový deštník, ale zapomněla
- 76. Nakreslete funkce Lineární
- 77. Děkuji za pozornost. Ekonomie 1, bakaláři,
Слайд 1Ekonomie 1 Bakaláři
První cvičení
Základní pojmy, zákony
a principy ekonomie
Jiří Mihola
jiri.mihola@quick.cz
+420 603
Слайд 5Klasická ekonomie se zabývá:
nabídkovou stranou trhu,
poptávkovou stranou trhu,
všeobecnou
monetární politikou.
Слайд 6Klasická ekonomie se zabývá:
nabídkovou stranou trhu,
poptávkovou stranou trhu,
všeobecnou
monetární politikou.
Слайд 8Jaká ekonomická věda se zabývá poptávkovou stranu trhu?
Marginalistická ekonomie jako část
Слайд 10Jak se liší mikroekonomie od makroekonomie?
Základními subjekty jsou:
podnikatelé, spotřebitelé
státy, národní ekonomika
Слайд 12Vymezení ekonomie
„Ekonomie je věda optimalizující využití vzácných zdrojů sloužících
Слайд 14Makroekonomie je věda zkoumající komplexní účinky chování ekonomických subjektů na celou
Слайд 16peníze
půda, budovy
stroje zařízení, nástroje
lidé se svými schopnostmi
………
Jakou formu má kapitál?
Слайд 18Z čeho plyne omezenost a tím i vzácnost výrobních faktorů?
Z toho,
Слайд 21Jakou ztrátu oproti nákladům obětované příležitosti utrpíte pokud vykonáváte optimální povolání?
Слайд 22Princip nákladů obětované příležitosti
Pokud realizujeme optimální
oproti každé jiné variantě nulová!
O nic nepřicházíme.
Слайд 24Jaké povolání je nejvhodnější?
Kde nejvíc vyděláte.
Pro které máte nejlepší schopnosti.
O které
Které vám doporučí rodiče.
Které vás nejvíc baví.
Слайд 25Jaké povolání je nejvhodnější?
Kde nejvíc vyděláte.
Pro které máte nejlepší schopnosti.
O které
Které vám doporučí rodiče.
Které vás nejvíc baví.
Слайд 27Je někdo schopen uspokojit všechny své potřeby osobně?
Jak lidé získávají ty
Слайд 28Je někdo schopen uspokojit všechny své potřeby osobně?
Jak lidé získávají ty
Za jakých podmínek bude získávání příjmů nejpříjemnější?
Слайд 29Otázky a příklady kap.1, str.34
Student VŠ dostává stipendium
3 000 PJ,
b) 18 000 PJ,
c) 25 000 PJ
d) 22 000 PJ.
Слайд 30Otázky a příklady kap.1, str.34
Student VŠ dostává stipendium 3 000 PJ. Kdyby
3 000 PJ,
b) 18 000 PJ,
c) 25 000 PJ
d) 22 000 PJ.
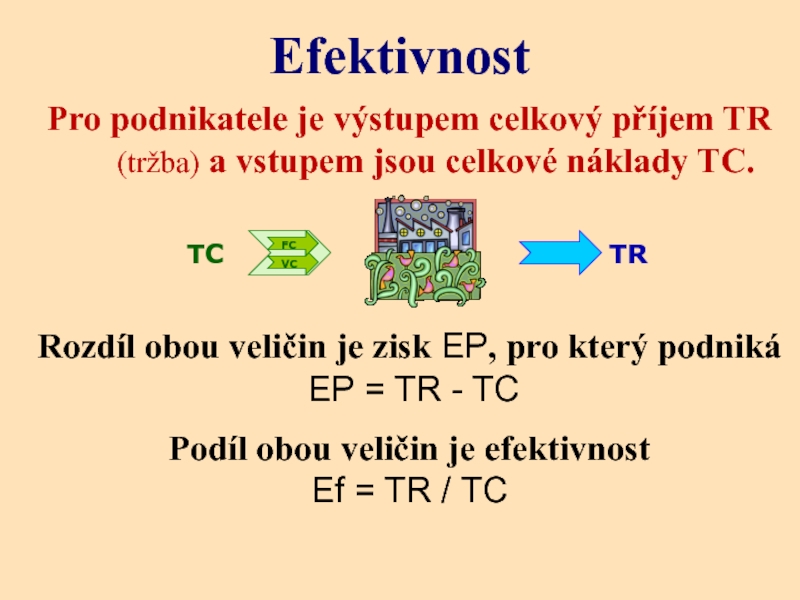
Слайд 32Efektivnost
Pro podnikatele je výstupem celkový příjem TR (tržba) a vstupem
Rozdíl obou veličin je zisk EP, pro který podniká
EP = TR - TC
Podíl obou veličin je efektivnost
Ef = TR / TC
TC
FC
VC
TR
Слайд 33Může se při stálé efektivnosti rozšiřovat produkce tak, že při tom
Ano, je to čistě intenzivní vývoj.
Ano, je to čistě extenzivní vývoj.
Ne, pokud neroste efektivnost, neroste ani zisk.
Ne, růst zisku je svázán s růstem efektivnosti.
Слайд 34Může se při stálé efektivnosti rozšiřovat produkce tak, že při tom
Ano, je to čistě intenzivní vývoj.
Ano, je to čistě extenzivní vývoj.
Ne, pokud neroste efektivnost, neroste ani zisk.
Ne, růst zisku je svázán s růstem efektivnosti.
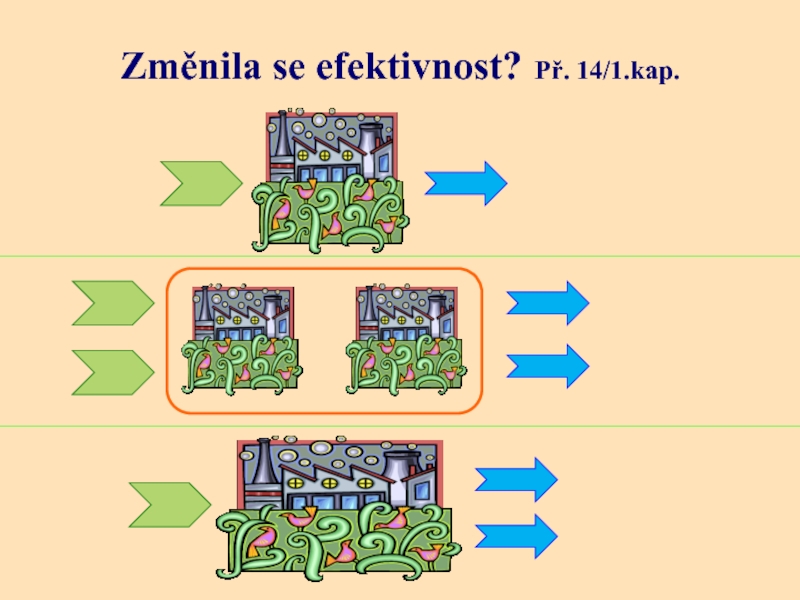
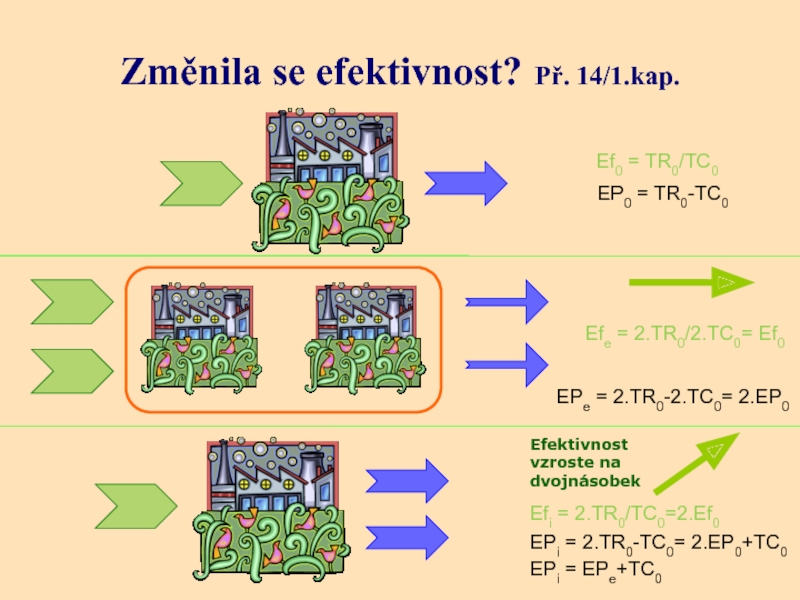
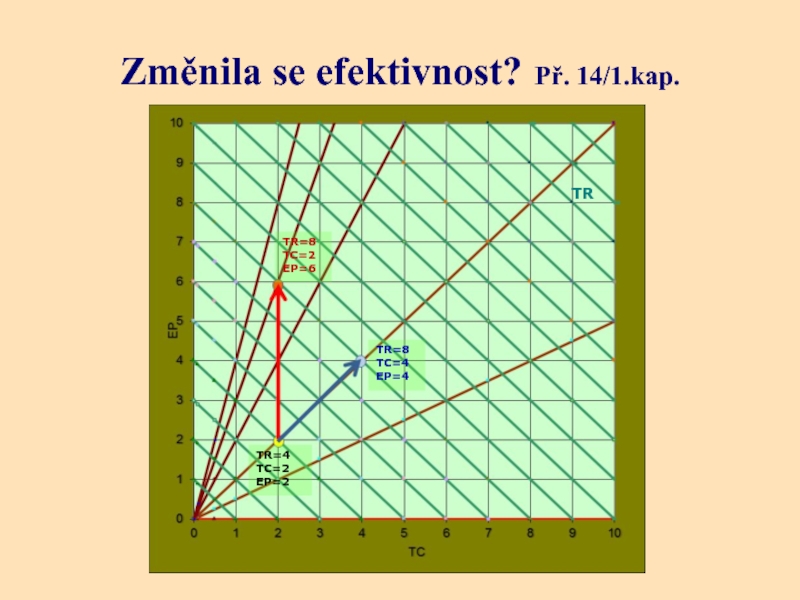
Слайд 37Změnila se efektivnost? Př. 14/1.kap.
Efe = 2.TR0/2.TC0= Ef0
Ef0 =
Efi = 2.TR0/TC0=2.Ef0
EP0 = TR0-TC0
EPe = 2.TR0-2.TC0= 2.EP0
EPi = 2.TR0-TC0= 2.EP0+TC0
EPi = EPe+TC0
Слайд 39Ekonomický zisk (EP) dostaneme tak, že od celkových příjmů odečteme:
jak účetní
pouze ACC
pouze OPC
Слайд 40Ekonomický zisk (EP) dostaneme tak, že od celkových příjmů odečteme:
jak účetní
pouze ACC
pouze OPC
Слайд 42Každý obchod by měl být paretovsky efektivní!!
Podstatou této efektivnosti je synergický
Слайд 45Numerický příklad na synergický efekt:
Optimálně získáte z 10 m2 cca 5
Běžně získáte z 10 m2 cca 3 q brambor – cena 20 Kč/kg
Optimálně získáte z 10 m2 cca 4 q zelí – cena 20 Kč/kg
Běžně získáte z 10 m2 jen cca 3 q zelí – cena 20 Kč
Слайд 46Numerický příklad na synergický efekt:
Optimálně získáte z 10 m2 cca 5
Běžně získáte z 10 m2 cca 3 q brambor – cena 20 Kč/kg
Optimálně získáte z 10 m2 cca 4 q zelí – cena 20 Kč/kg
Běžně získáte z 10 m2 jen cca 3 q zelí – cena 20 Kč
Synergický efekt [(5-3).20 + (4-3).20].100 = 6 000 Kč
Слайд 56Hranice produkčních možností PPF
je maximální možná
Слайд 58Otázky a příklady kap.1, str.34; př. 9
Nakreslete hranici
(1, 20), (2, 18), (3, 15), (4, 11), (5, 6), (6, 0).
Слайд 60Otázky a příklady kap.1, str.34; př. 10
Na základě
pokud díky technologické inovaci může zvýšit produkci obou statků,
pokud v důsledku požáru musí snížit produkci obou statků.
Слайд 62Hranice produkčních možností PPF Meze Q´2? pro Q´1=25
Máte-li
Q´1=25
Слайд 67Otázky a příklady kap.1, str.34; př.24
Na základě hodnot uvedených v příkladu
Слайд 74Marie si koupila nový deštník, ale zapomněla jej v metru, odkud
náklady obětované příležitosti,
transakční náklady,
utopené náklady,
reprodukční náklady,
Průměrné náklady.
Слайд 75Marie si koupila nový deštník, ale zapomněla jej v metru, odkud
náklady obětované příležitosti,
transakční náklady,
utopené náklady,
reprodukční náklady,
Průměrné náklady.
Слайд 76Nakreslete funkce
Lineární rostoucí y = F (x) =
a < 0 b) a = 0 c) a > 0
2) Nelineární rostoucí y = F (x)
konkávní b) konvexní c) s inflexním bodem
3) Nakreslete funkci
konstanty b) periodickou c) neklesající
4) Nakreslete nějakou funkci
sudou (x2) b) lichou (x3) c) y = │x│