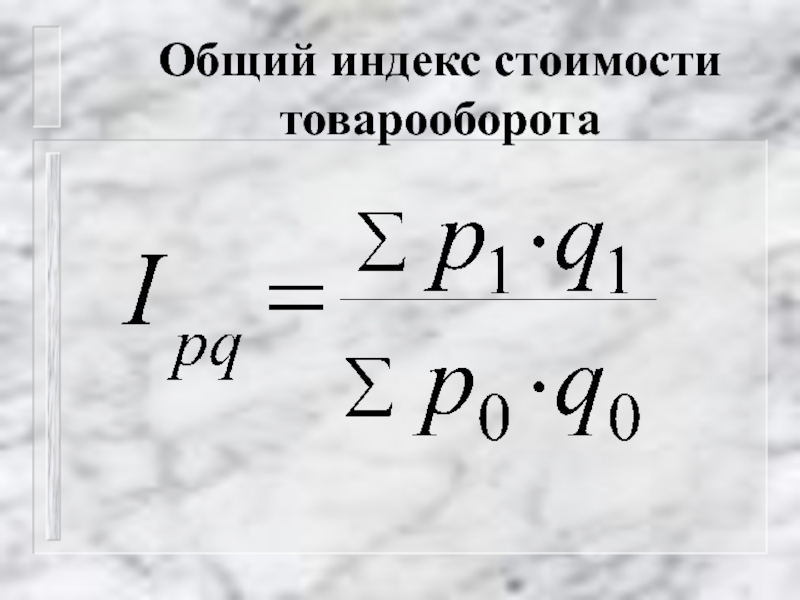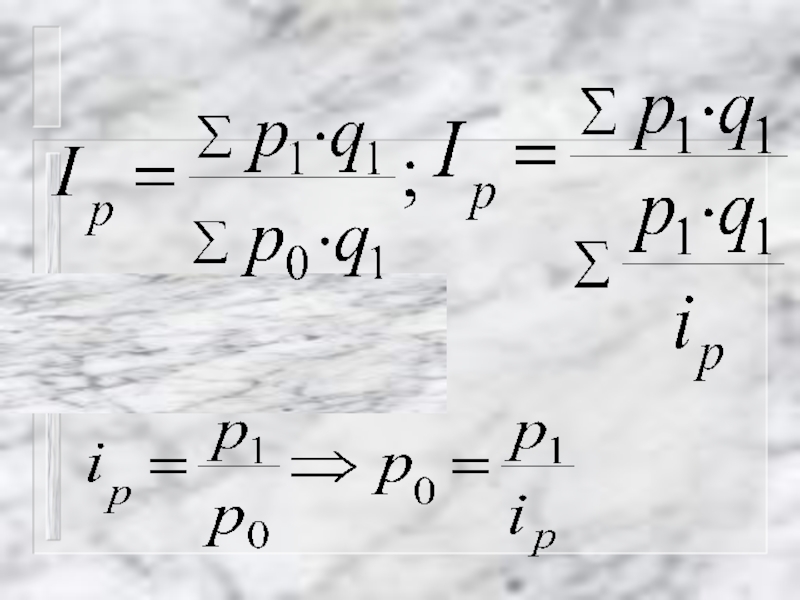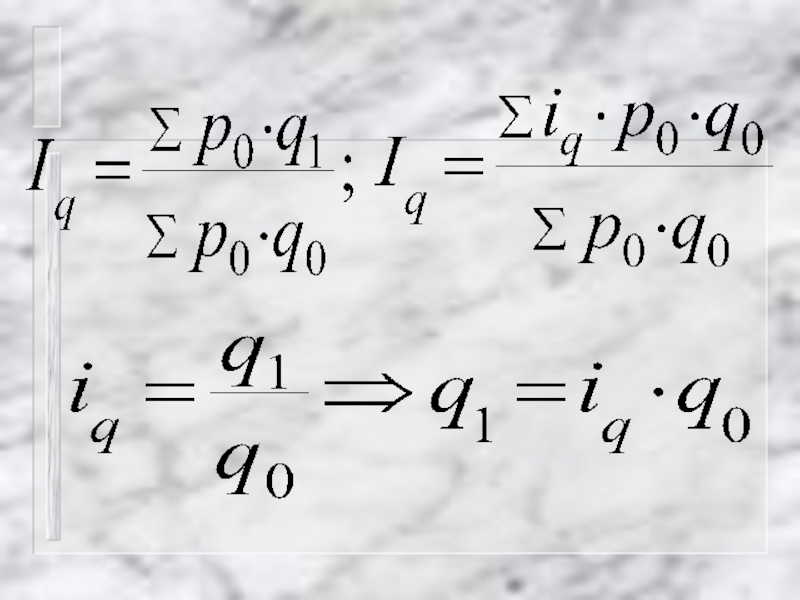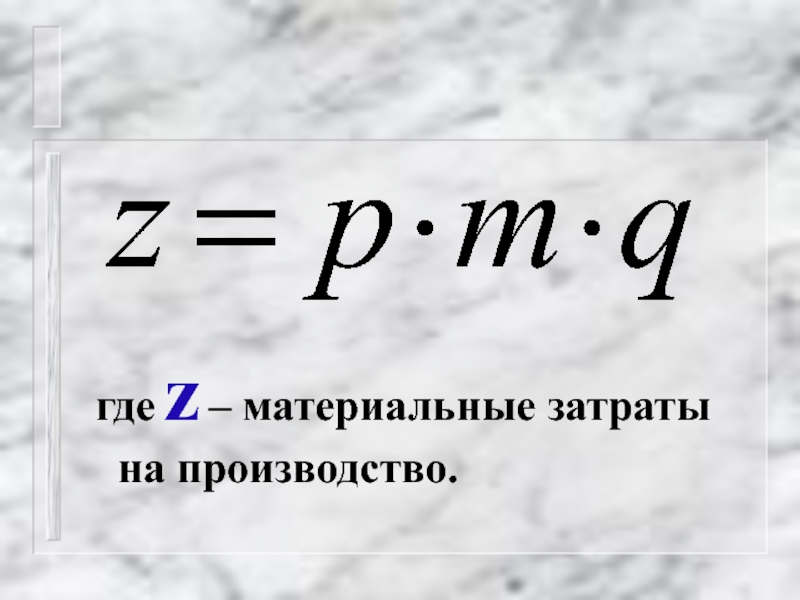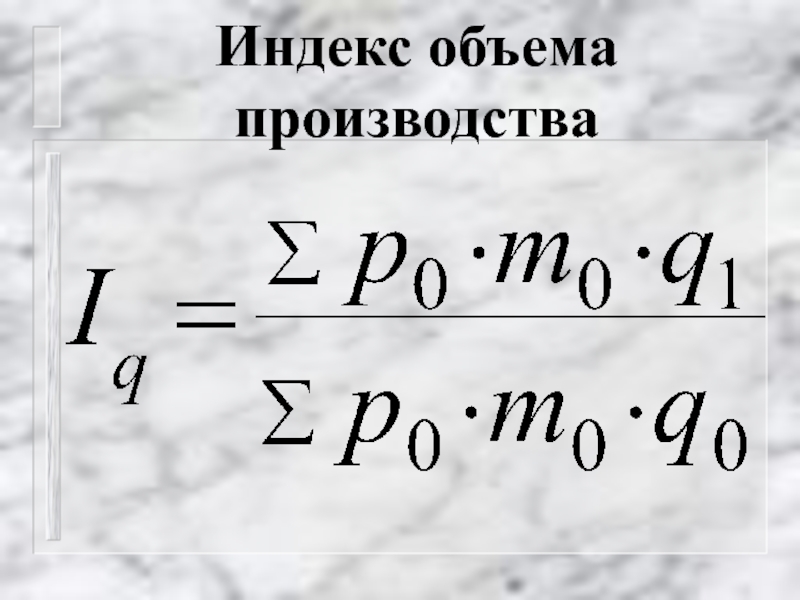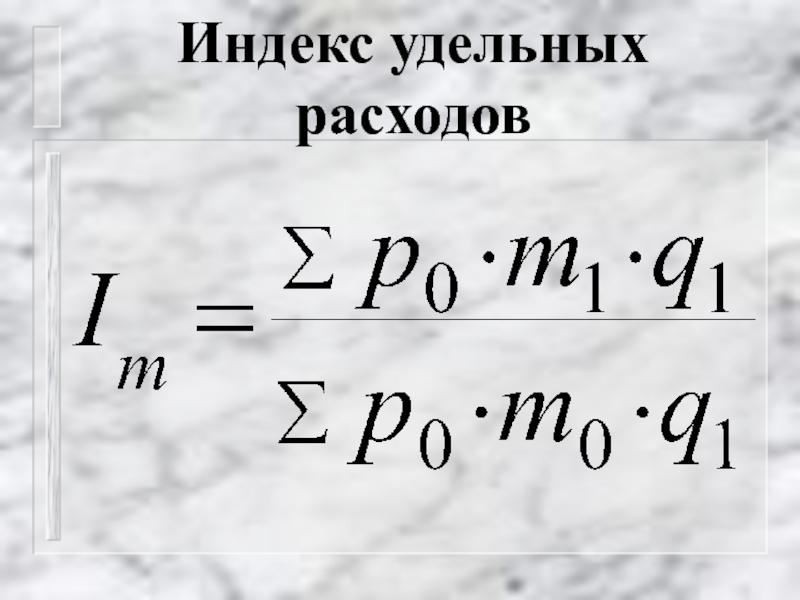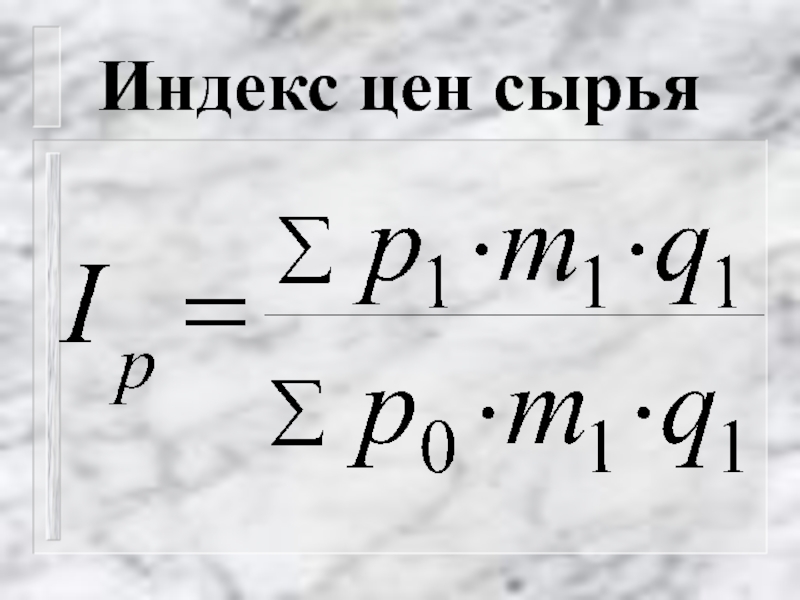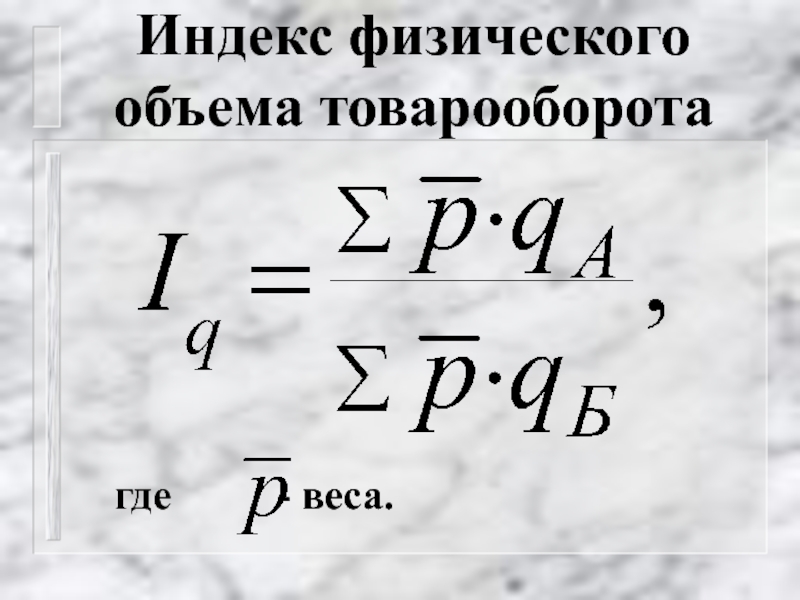- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экономические индексы презентация
Содержание
- 1. Экономические индексы
- 2. Индексами в статистике называются обобщающие показатели
- 3. Индексный метод применяется для решения следующих задач:
- 4. Индексы подразделяются на индивидуальные и общие (сводные).
- 5. Индивидуальным называется индекс, который применяется для
- 6. Индивидуальный индекс цены
- 7. Индивидуальный индекс физического объема товарооборота где
- 8. Индивидуальный индекс товарооборота
- 10. Общим индексом называется относительный показатель,
- 11. Идея построения общего индекса цен
- 12. На величину товарооборота влияют два фактора:
- 13. Возможны два варианта: 1. Количество проданных товаров
- 14. 2. Количество проданных товаров фиксируется на уровне базисного
- 15. Для получения единого результата используется индекс Фишера,
- 16. Общий индекс физического объема товарооборота
- 17. Общий индекс стоимости товарооборота
- 18. Эти индексы представляют собой систему:
- 19. или:
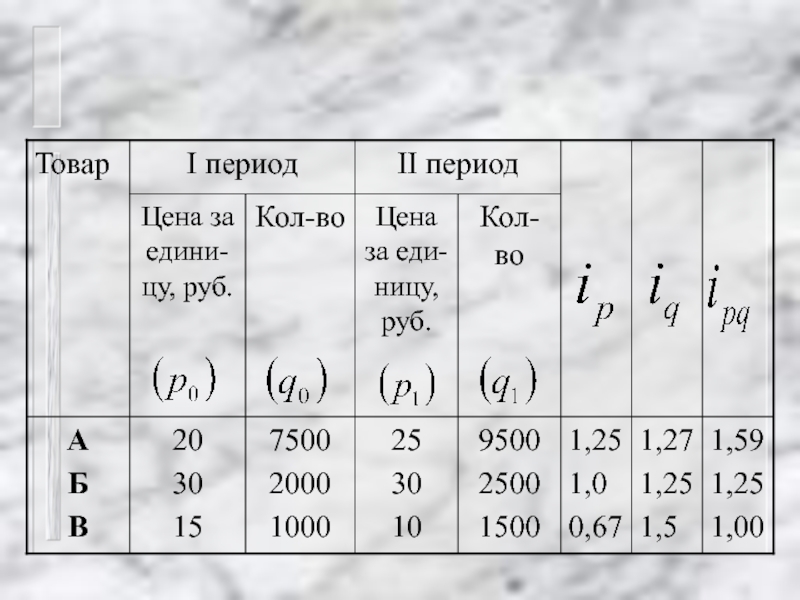
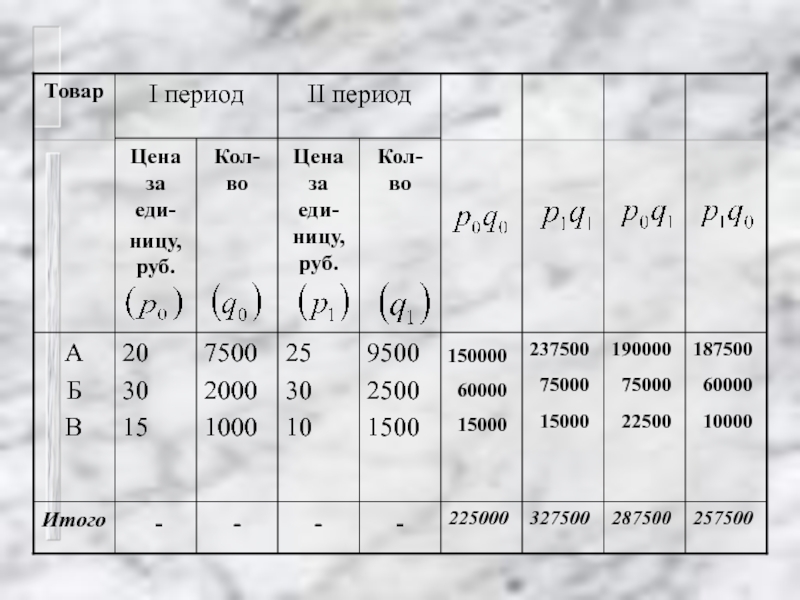
- 20. 150000 60000 15000
- 21. Факторный анализ Для анализа влияния отдельных факторов
- 22. 1. Абсолютное изменение товарооборота (числитель минус знаменатель индекса стоимости товарооборота):
- 23. Факторный анализ Прирост стоимости товарооборота происходит под
- 24. Факторный анализ Для получения сопоставимых результатов рекомендуется
- 25. 2. Абсолютное изменение товарооборота за счет изменения
- 26. 3. Абсолютное изменение товарооборота за счет изменения
- 27. Взаимосвязь абсолютных величин
- 28. Средний гармонический индекс
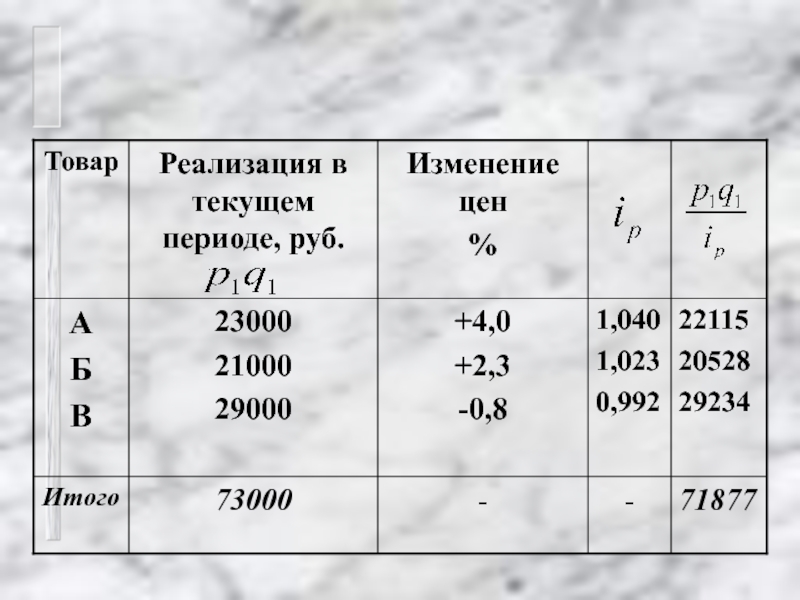
- 30. В данном случае общий индекс цен
- 32. Цены по данной товарной группе в текущем
- 33. Средний арифметический индекс
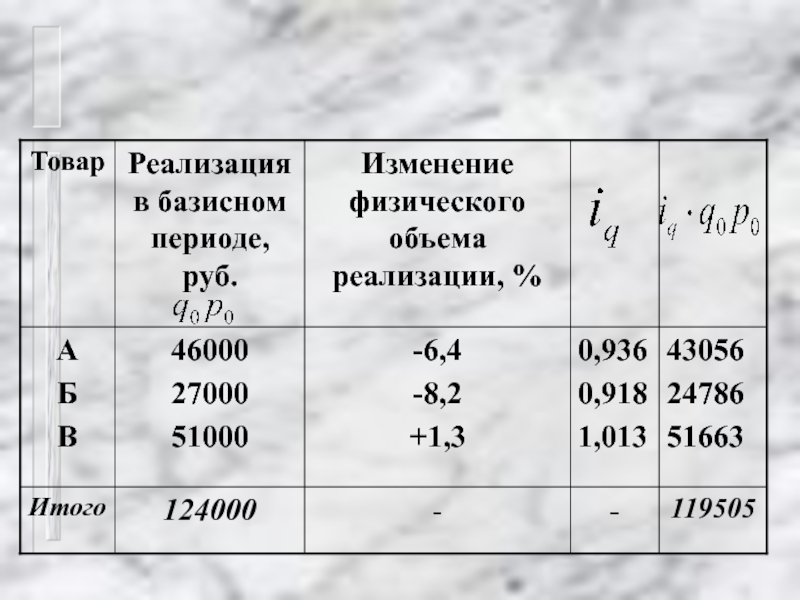
- 35. В данном случае общий индекс физического
- 37. Физический объем реализации данных товаров в среднем снизился на 3,6%
- 38. Индексы средних уровней (индексы переменного состава, постоянного состава и структурных сдвигов)
- 39. Рассматривается реализация товара А несколькими фирмами. У
- 40. .Индекс средней цены (Индекс переменного состава)
- 41. Из формулы индекса переменного состава
- 42. 1. Субиндекс - индекс постоянного состава.
- 43. 2. Субиндекс - индекс структурных сдвигов.
- 44. Перечисленные индексы образуют систему:
- 45. 1. Абсолютное изменение средней цены исчисляется
- 46. 2. Изменение средней цены за счет изменения цен
- 47. 3. Изменение средней цены за счет структурных сдвигов
- 48. Перечисленные абсолютные величины образуют систему:
- 49. Трехфакторные индексы
- 50. Cтоимость материальных затрат на производство продукции зависит
- 51. где z – материальные затраты на производство.
- 52. Индекс материальных затрат на производство
- 53. Индекс объема производства
- 54. Индекс удельных расходов
- 55. Индекс цен сырья
- 56. Эти индексы образуют систему
- 57. Территориальные индексы
- 58. При построении территориальных индексов возникают вопросы о
- 59. В качестве весов берем количество товаров, проданных в регионе А.
- 60. В качестве весов берем количество товаров, проданных в регионе Б.
- 61. Данные индексы не взаимосвязаны между собой:
- 62. Для получения единого результата в качестве весов используется суммарный объем продаж двух регионов.
- 63. Возможно построение индекса цен на основе метода косвенной стандартизации.
- 64. где - средняя цена для двух регионов.
- 65. Индекс физического объема товарооборота где - веса.
- 66. Индекс товарооборота по двум регионам
- 67. Цепные и базисные индексы
- 68. Если индексы рассчитываются для большего, чем два,
- 69. Индивидуальные индексы
- 70. Рассмотрим реализацию какого-либо товара в разные периоды времени.
- 72. - количество проданного товара в базисном
- 73. Произведение цепных индексов дает базисный индекс последнего периода времени.
- 74. Общие индексы
- 75. Отмеченная выше взаимосвязь безусловна только для индивидуальных
- 76. Пусть имеются данные о реализации нескольких товаров за четыре периода времени.
- 77. Система базисных индексов За базисный принимается первый по порядку период времени.
- 78. Система цепных индексов с постоянными весами
- 80. Система цепных индексов с переменными весами
- 82. Iq = Σ iq q0 p0
Индексами в статистике называются обобщающие показатели сравнения во времени или пространстве величин какого-либо общественного явления.
Слайд 2 Индексами
в статистике называются обобщающие показатели сравнения во времени или пространстве
величин какого-либо общественного явления.
Слайд 3Индексный метод применяется для решения следующих задач:
для изучения изменения явлений во
времени;
для проведения пространственных сравнений;
для характеристики степени выполнения плана;
для характеристики степени влияния структурных изменений.
для проведения пространственных сравнений;
для характеристики степени выполнения плана;
для характеристики степени влияния структурных изменений.
Слайд 5Индивидуальным называется индекс, который применяется для определения степени изменения отдельного элемента
сложного общественного явления.
Слайд 7Индивидуальный индекс физического объема товарооборота
где q1 – количество проданного товара
в отчетном периоде;
q0 – количество проданного товара в базисном периоде.
q0 – количество проданного товара в базисном периоде.
Слайд 10 Общим индексом называется относительный показатель, характеризующий изменение сложного явления, состоящего из
элементов, не поддающихся непосредственному суммированию.
Слайд 11Идея построения
общего индекса цен
Общий индекс цен показывает, как в среднем
меняются цены по всем рассматриваемым товарным группам.
Так как цены, относящиеся к различным товарам, непосредственно суммировать нельзя, то нужно выбрать некий показатель, чтобы действие суммирования имело смысл.
Таким показателем является товарооборот или выручка
Так как цены, относящиеся к различным товарам, непосредственно суммировать нельзя, то нужно выбрать некий показатель, чтобы действие суммирования имело смысл.
Таким показателем является товарооборот или выручка
Слайд 12На величину товарооборота влияют два фактора:
уровень цен;
количество проданных товаров.
Так как нас
интересует только изменение цен, то влияние второго фактора необходимо устранить. Для этого количество проданных товаров фиксируется на постоянном уровне.
Слайд 13Возможны два варианта:
1. Количество проданных товаров фиксируется на уровне отчетного периода:
где
- индекс Пааше
Слайд 142. Количество проданных товаров фиксируется на уровне базисного периода:
где
- индекс цен Ласпейреса
Слайд 15Для получения единого результата используется индекс Фишера, который рассчитывается как средняя
геометрическая величина из индексов Пааше и Ласпейреса:
Слайд 16
Общий индекс
физического объема товарооборота
Данный индекс показывает, как изменяется общая выручка
в связи с изменением количества проданных товаров
Слайд 21Факторный анализ
Для анализа влияния отдельных факторов на прирост товарооборота берут разность
между числителем и знаменателем соответствующего общего индекса
Слайд 221. Абсолютное изменение товарооборота (числитель минус знаменатель индекса стоимости товарооборота):
Слайд 23Факторный анализ
Прирост стоимости товарооборота происходит под влиянием двух факторов: изменения количества
проданных товаров и изменения цены за единицу товара. Сумма приростов под влиянием этих факторов должна равняться общему приросту стоимости товарооборота
Слайд 24Факторный анализ
Для получения сопоставимых результатов рекомендуется соблюдать такую последовательность включения факторов
в анализ: вначале идут количественные факторы (в нашем случае q), затем качественные (Р)
Слайд 252. Абсолютное изменение товарооборота за счет изменения количества проданных товаров (числитель
минус знаменатель общего индекса физического объема товарооборота по Ласпейресу):
Слайд 263. Абсолютное изменение товарооборота за счет изменения цен (числитель минус знаменатель
индекса цен по Пааше):
Здесь возможны два случая:
экономия или
перерасход покупателей за счет изменения цен
Слайд 30В данном случае общий индекс цен рассчитывается как средняя гармоническая величина
из индивидуальных индексов, где в качестве весов выступают величины товарооборота отчетного периода.
Слайд 32Цены по данной товарной группе в текущем периоде по сравнению с
базисным в среднем возросли на 1,6%
Слайд 35В данном случае общий индекс физического объёма товарооборота рассчитывается как средняя
арифметическая величина из индивидуальных индексов физического объема товарооборота , где в качестве весов выступают величины товарооборота базисного периода:
Слайд 38Индексы средних уровней
(индексы переменного состава, постоянного состава и структурных сдвигов)
Слайд 39 Рассматривается реализация товара А несколькими фирмами. У каждой фирмы определенный объем
реализации и своя цена.
Требуется проанализировать, как изменяется средняя цена товара
Слайд 41Из формулы индекса переменного состава видно, что средняя цена изменяется в
результате действия двух факторов:
изменение цен в отдельных фирмах;
изменение удельного веса фирм в общем объеме реализации товаров.
Следовательно, индекс переменного состава может быть разложен на два субиндекса, каждый из которых характеризует действия одного из этих факторов
Слайд 421. Субиндекс - индекс постоянного состава. Он показывает, как изменяется средняя цена
в результате изменения цен в отдельных фирмах.
Слайд 432. Субиндекс - индекс структурных сдвигов. Он показывает, как изменяется средняя цена
в результате изменения удельного веса фирм в общем объеме реализации товаров (в результате структурных сдвигов):
Слайд 451. Абсолютное изменение средней цены исчисляется как разность делимого и делителя индекса
переменного состава
Слайд 462. Изменение средней цены за счет изменения цен в отдельных фирмах
исчисляется как разность делимого и делителя индекса фиксированного состава:
Слайд 473. Изменение средней цены за счет структурных сдвигов исчисляется как разность
делимого и делителя индекса структурных сдвигов:
Слайд 50Cтоимость материальных затрат на производство продукции зависит от:
q - количества
выпускаемой продукции ;
m - удельных расходов сырья и материалов ;
p - цен на сырье и материалы.
m - удельных расходов сырья и материалов ;
p - цен на сырье и материалы.
Слайд 58 При построении территориальных индексов возникают вопросы о базе сравнения и объекте,
на уровне которого следует зафиксировать веса индекса.
Эти вопросы решаются, исходя из конкретных задач исследования.
Например, необходимо сравнить уровни цен двух регионов
(регионов А и Б).
Эти вопросы решаются, исходя из конкретных задач исследования.
Например, необходимо сравнить уровни цен двух регионов
(регионов А и Б).
Слайд 62Для получения единого результата в качестве весов используется суммарный объем продаж
двух регионов.
Слайд 68 Если индексы рассчитываются для большего, чем два, числа периодов времени, то
они могут быть получены базисным и цепным способом.
Рассмотрим построение базисных и цепных индексов на примере индекса физического объема товарооборота.
Рассмотрим построение базисных и цепных индексов на примере индекса физического объема товарооборота.
Слайд 72 - количество проданного товара в базисном периоде;
- количество проданного
товара в первом периоде и так далее.
Слайд 75 Отмеченная выше взаимосвязь безусловна только для индивидуальных индексов.
Для общих же
индексов эта взаимосвязь будет справедлива лишь тогда, когда общие индексы будут рассчитываться с так называемыми постоянными весами.
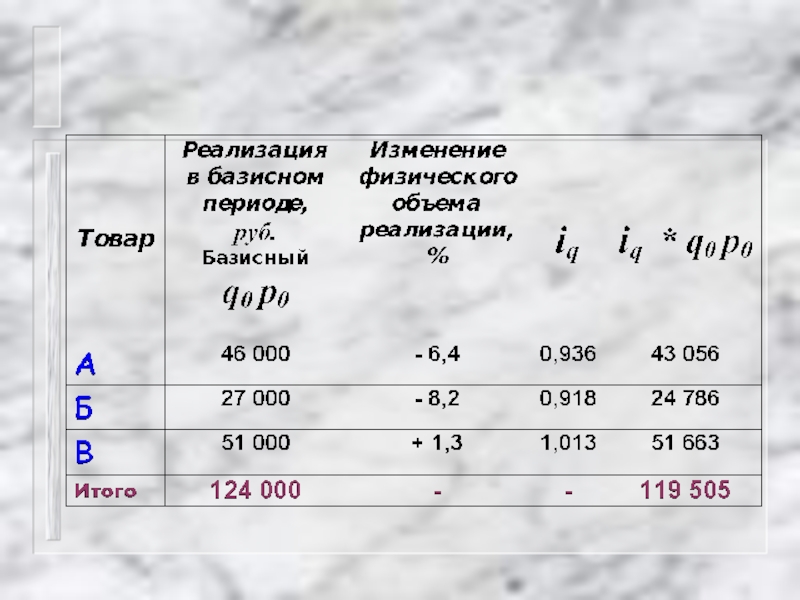
Слайд 82
Iq = Σ iq q0 p0 / Σ q0 p0 =
=119 505 / 124 000 =
0, 964 или 96,4 %
Физический объем реализации данных товаров в среднем снизился на 3,6 %
