- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дуополия и теория игр презентация
Содержание
- 1. Дуополия и теория игр
- 2. Введение При олигополистической структуре рынка фирма более
- 3. Олигополия характеризуется стратегическим поведением фирм Стратегическое поведение
- 4. некооперативное взаимодействие (самостоятельная политика на рынке
- 5. Дуополия – частный случай олигополии, когда на
- 6. Классификация моделей некооперативных стратегий поведения
- 7. 2. Теория игр: основные элементы анализа Предмет
- 8. Цели теории игр Анализ и объяснение ситуаций
- 9. Полезность и выгода Для теории игр безразлично,
- 10. Основные определения: Игрок - это лицо, принимающее
- 11. Игра в нормальной форме Одношаговая Игроки не
- 12. Симметричная информация У каждого игрока информационное множество
- 13. Равновесие по Нэшу в смешанных стратегиях У
- 14. Игра 2 лиц в общем виде
- 15. Решение проблемы На практике (игра «Недоросль») изменить
- 16. Смешанная стратегия Смешанная стратегия – это вероятностное
- 17. Теорема Нэша (1950) Ref J.F.Nash. Equilibrium Points
- 18. Кооперативные игры Игра называется кооперативной, если игроки
- 19. Аксиоматическая теория переговоров Что должен рекомендовать сторонам
- 20. Аксиомы решения по Нэшу (1950) Оптимальность по
- 21. Полезные выводы Каждая из сторон может обладать
- 22. 3. Модели дуополии. Модель Курно Задача каждого
- 23. Дуополия: модель Курно Функции общих прибылей игроков:
- 24. q2 q1 900 q1m = 450
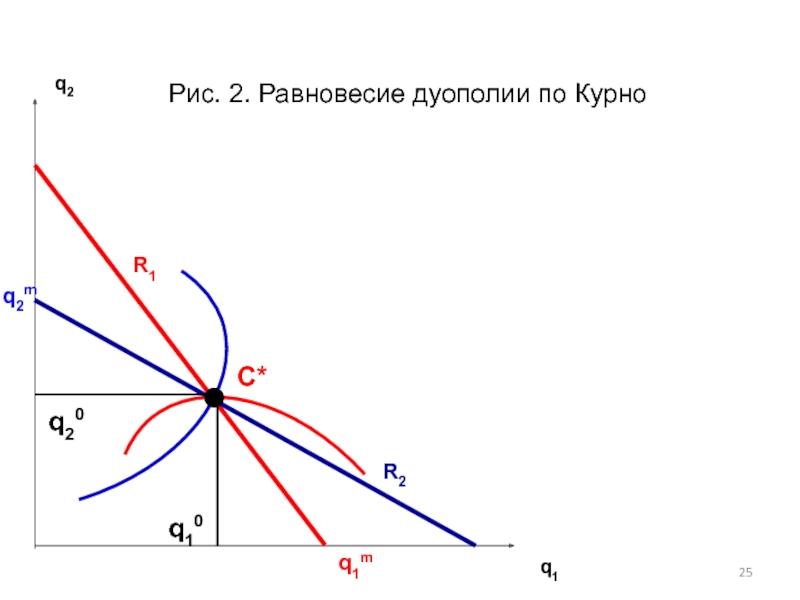
- 25. q2 q1 q2m q20
- 26. Дуополия: модель Бертрана Критика Бертраном модели Курно.
- 27. Дуополия: модель Бертрана В классической модели Бертрана
- 28. Однородность продукта: покупатели предпочтут продукцию фирмы, назначившей
- 29. Равновесие в простой модели ценовой конкуренции Бертрана:
- 30. «Слабые места» модели Бертрана: Однородность продукции →
- 31. Одна из фирм установит объем выпуска первой,
- 32. Пусть лидером будет первая фирма, последователем –
- 33. На рис.3. равновесие дуополии по Штакельбергу показано
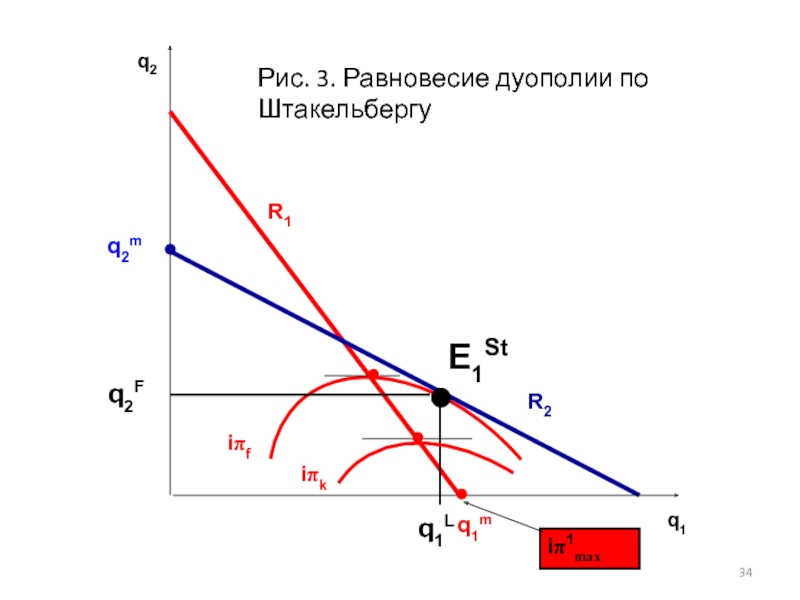
- 34. q2 q1 q2m q2F q1L q1m E1St
- 35. Дуополия: модель Форхаймера Модель Форхаймера – это
- 36. Ограничения в модели Форхаймера Издержки доминирующей фирмы
- 37. Этапы формирования цены: Лидер предлагает последователям продавать
Слайд 1Тема 11. Дуополия и теория игр
Дуополия: понятие и подходы к анализу
Теория игр: основные элементы анализа
Модели дуополии
Слайд 2Введение
При олигополистической структуре рынка фирма более не сталкивается с пассивным окружением,
Слайд 3Олигополия характеризуется стратегическим поведением фирм
Стратегическое поведение фирмы – такое поведение, когда
1. Дуополия: понятие и подходы к анализу
Слайд 4 некооперативное взаимодействие (самостоятельная политика на рынке + конкуренция с другими
кооперативное поведение (сговор + совместные действия на рынке)
Стратегическое поведение осуществляется в двух формах:
Слайд 5Дуополия – частный случай олигополии, когда на рынке действуют два игрока
Объем продаж делится между двумя игроками
От решений об объемах выпуска каждого участника зависит уровень рыночной цены и, следовательно, возможности извлечения прибыли
Дуополия: понятие и характеристика
Слайд 72. Теория игр: основные элементы анализа
Предмет теории игр:
Ситуации, в которых есть
Интересы субъектов могут быть как противоположными (военные конфликты), так и просто не совпадающими.
Слайд 8Цели теории игр
Анализ и объяснение ситуаций в различных предметных областях
Выработка рекомендаций
Основные понятия: игроки (субъекты), действия, платежи и информация
Слайд 9Полезность и выгода
Для теории игр безразлично, что получают субъекты от игры:
Игроки могут получать выгоду в разных единицах измерения.
Выгода каждого игрока
может быть измерена одним числом;
может быть положительной или отрицательной;
известна игрокам.
Слайд 10Основные определения:
Игрок - это лицо, принимающее решения. Целью каждого игрока является
Действие или ход игрока — выбор одной из нескольких доступных для этого игрока альтернатив поведения.
Информация в игре — вероятностное знание ходов природы и других игроков
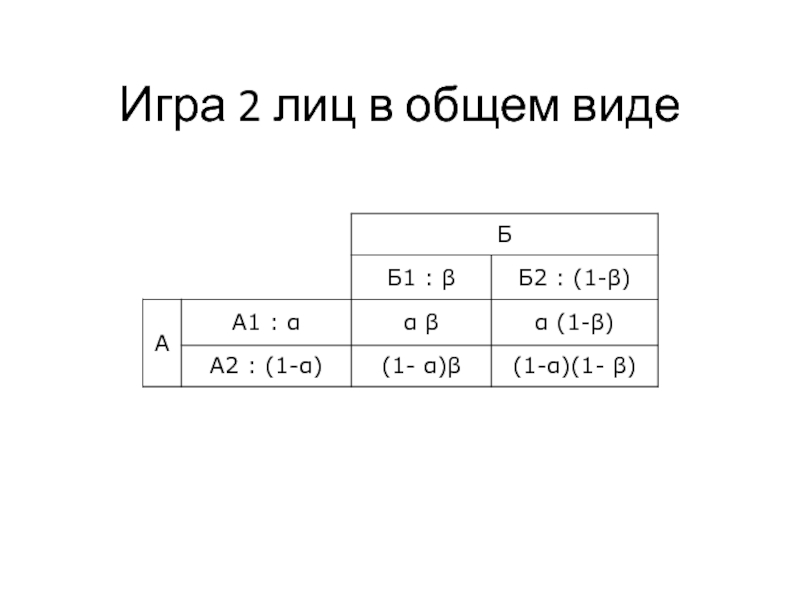
Слайд 11Игра в нормальной форме
Одношаговая
Игроки не знают выбора друг друга
Чистая стратегия =
Представление:
2 игрока — в форме платежной матрицы
>2 игроков — пары (действия; платежи)
Слайд 12Симметричная информация
У каждого игрока информационное множество в моменты принятия им решений
Игра будет симметричной тогда, когда соответствующие стратегии у игроков будут равны, то есть иметь одинаковые платежи. Например, «Дилемма заключённого».
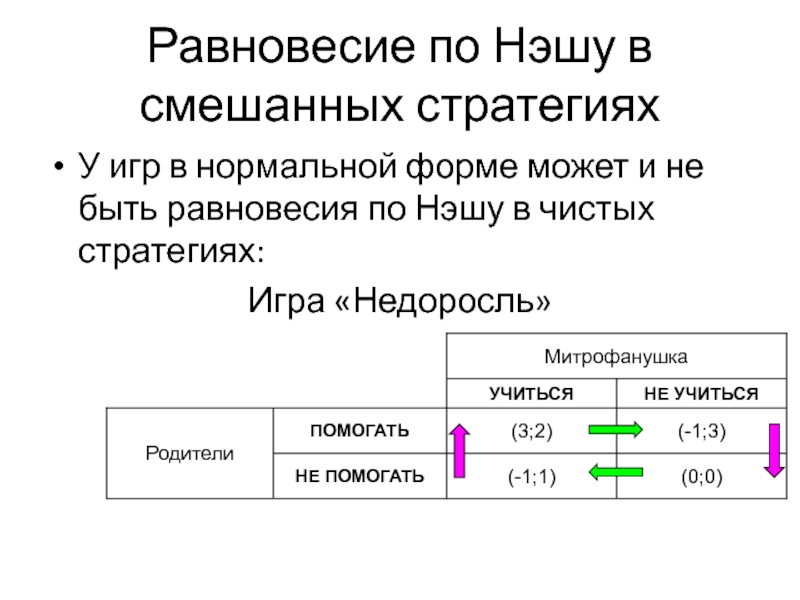
Слайд 13Равновесие по Нэшу в смешанных стратегиях
У игр в нормальной форме может
Игра «Недоросль»
Слайд 15Решение проблемы
На практике (игра «Недоросль»)
изменить правила игры, улучшить контроль и мотивацию
В теории
ввести понятие смешанной стратегии.
Слайд 16Смешанная стратегия
Смешанная стратегия – это вероятностное распределение на пространстве действий игрока
Число действий:
конечно (счетно)?дискретное распределение
несчетно ? непрерывное распределение
Слайд 17Теорема Нэша (1950)
Ref J.F.Nash. Equilibrium Points in N-Person Games. Proceedings of
У каждой конечной игры существует равновесие в смешанных стратегиях
Слайд 18Кооперативные игры
Игра называется кооперативной, если игроки могут объединяться в группы, беря
Кооперативные игры отличаются целями, а не коммуникацией игроков.
Соглашение между участниками о стратегиях поведения будет выполнено, поскольку:
«Договоры надо исполнять»
По внутреннему убеждению или по внешнему принуждению
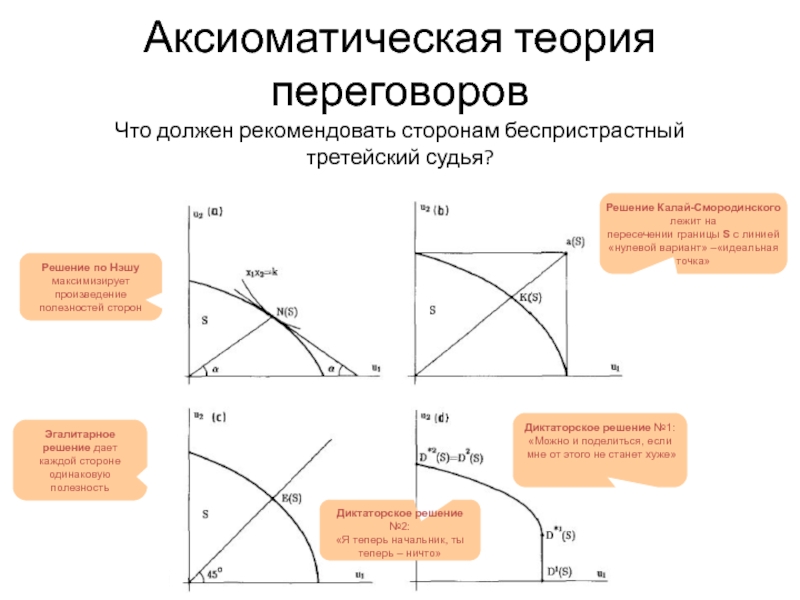
Слайд 19Аксиоматическая теория переговоров
Что должен рекомендовать сторонам беспристрастный третейский судья?
Решение по Нэшу
Решение Калай-Смородинского лежит на
пересечении границы S с линией «нулевой вариант» –«идеальная точка»
Эгалитарное решение дает каждой стороне одинаковую полезность
Диктаторское решение №2:
«Я теперь начальник, ты теперь – ничто»
Диктаторское решение №1:
«Можно и поделиться, если мне от этого не станет хуже»
Слайд 20Аксиомы решения по Нэшу (1950)
Оптимальность по Парето: ни одна сторона не
Симметричность: если в формулировке задачи нет различий между сторонами, то и решение должно быть симметричным
Анонимность
Независимость от соотношения масштабов полезностей сторон и сторонних альтернатив.
Слайд 21Полезные выводы
Каждая из сторон может обладать различным влиянием (1 и 2,
Обычное решение по Нэшу:
maxS u1·u2
Взвешенное решение по Нэшу:
maxS u11 ·u22
Решение по Нэшу характеризуется свойством индивидуальной рациональности для каждого игрока
Слайд 223. Модели дуополии. Модель Курно
Задача каждого игрока – выбрать объем выпуска
Фирмы производят однородный продукт и знают функцию рыночного спроса
Отраслевая функция сбыта определяется так:
p(q1 + q2) = D-1
Слайд 23Дуополия: модель Курно
Функции общих прибылей игроков:
Tπ1(q1,q2) = [p(q1 + q2)]q1
Tπ2(q2,q1) = [p(q1 + q2)]q2 – TC(q2)
Каждый игрок максимизирует собственную общую прибыль, выбирая для себя объем выпуска (с учетом решений конкурента)
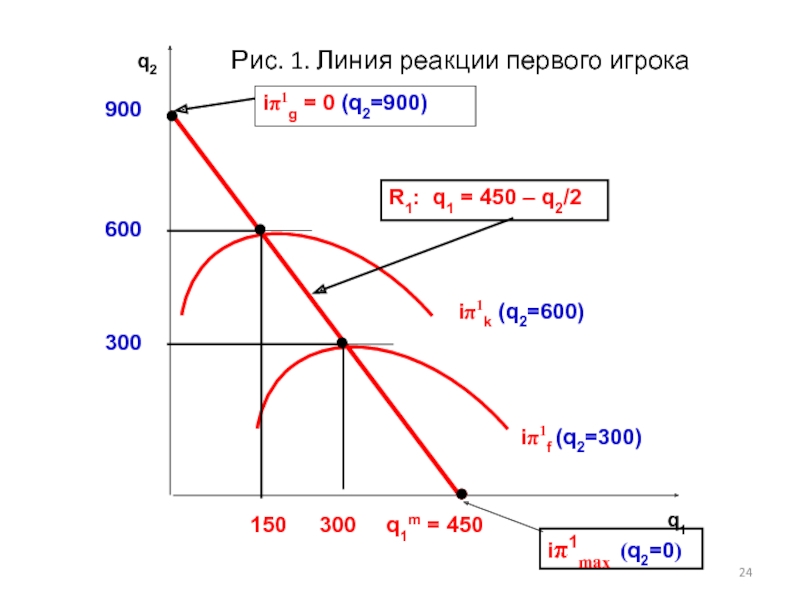
Изопрофита – кривая равной прибыли – отражает возможности получения прибыли конкретным игроком на неизменном уровне при различном распределении выпусков (рис.1).
Слайд 24
q2
q1
900
q1m = 450
R1: q1 = 450 – q2/2
iπ1k (q2=600)
iπ1max (q2=0)
iπ1f
Рис. 1. Линия реакции первого игрока
300
600
150
300
iπ1g = 0 (q2=900)
Слайд 26Дуополия: модель Бертрана
Критика Бертраном модели Курно.
Олигополисты назначают цены, а не объемы.
Последовательность
1) Фирмы назначают цены pj (одновременно)
2) Покупатели решают, у какой фирмы и сколько покупать.
Слайд 27Дуополия: модель Бертрана
В классической модели Бертрана издержки на единицу продукции считаются
Фирмы могут производить благо в произвольном количестве при одних и тех же предельных издержках.
Спрос на продукцию фирмы зависит также от цен, назначенных другими.
Выигрыш - это прибыль в зависимости от назначенных цен.
Слайд 28Однородность продукта: покупатели предпочтут продукцию фирмы, назначившей меньшую цену, тогда фирма
При назначении фирмами одинаковых цен покупателям безразлично – продукцию которой из фирм приобретать. Следовательно, объемы продаж у фирм одинаковы
Дуополия: модель Бертрана
Слайд 29Равновесие в простой модели ценовой конкуренции Бертрана:
Фирмы назначат цены на
p1 = MC1 = C; p2 = MC2 = C p1 = p2
и нет стимулов для увеличения/снижения цен → равновесие Нэша: наилучшее поведение каждого игрока при данном поведении конкурента
Каждый игрок в равновесии получает нулевую экономическую прибыль (если FC = 0):
Tπ1 = Tπ2 = 0
Дуополия: модель Бертрана
Слайд 30«Слабые места» модели Бертрана:
Однородность продукции → естественно конкурировать по объемам, а
Равномерное распределение объемов при назначении одинаковых цен – не всегда.
«Сильная сторона» модели Бертрана:
Позволяет выявить существенные различия равновесия по Нэшу в зависимости от выбора стратегической переменной (объем или цена)
Дуополия: модель Бертрана
Слайд 31Одна из фирм установит объем выпуска первой, т.е. получит преимущество первого
Лидер знает все возможные «ходы» последователя – его функцию реакции (RF) и максимизирует свою прибыль
При последовательном принятии решений в отрасли устанавливается равновесие дуополии по Штакельбергу
Дуополия: модель Штакельберга
Слайд 32Пусть лидером будет первая фирма, последователем – вторая
Тогда функции общих
Tπ1L(q1,q2(q1)) = [p(q1 + q2(q1))]q1 – TC(q1)
Tπ2F(q2,q1) = [p(q1 + q2)]q2 – TC(q2)
Дуополия: модель Штакельберга
Слайд 33На рис.3. равновесие дуополии по Штакельбергу показано точкой E1St с координатами
Нахождение равновесия дуополии по Штакельбергу графическим методом предполагает поиск точки, в которой линия реакции последователя (R2) является касательной к одной из изопрофит лидера
Дуополия: модель Штакельберга
Слайд 35Дуополия: модель Форхаймера
Модель Форхаймера – это ситуация, когда одну активную фирму
Но, войдя на рынок, крупная фирма предпринимает попытку занять определенную долю на нем.
Слайд 36Ограничения в модели Форхаймера
Издержки доминирующей фирмы ниже, издержек фирм–аутсайдеров. Более того,
Количество фирм–аутсайдеров фиксировано;
Аутсайдеры производят равное количество изделий;
Доминирующая фирма знает спрос на продукцию;
Фирмы–аутсайдеры ориентируются по цене на лидера
Слайд 37Этапы формирования цены:
Лидер предлагает последователям продавать продукцию по цене, превышающей издержки.
Фирмы-последователи,
Тогда на долю лидера выпадает остаточный спрос.
Лидер выбирает оптимальную цену, исходя из максимизации прибыли на остаточном спросе.


















![Дуополия: модель КурноФункции общих прибылей игроков: Tπ1(q1,q2) = [p(q1 + q2)]q1 – TC(q1)Tπ2(q2,q1) = [p(q1](/img/tmb/5/459621/3e5b48292409453f87dbc12ef15f4bc4-800x.jpg)