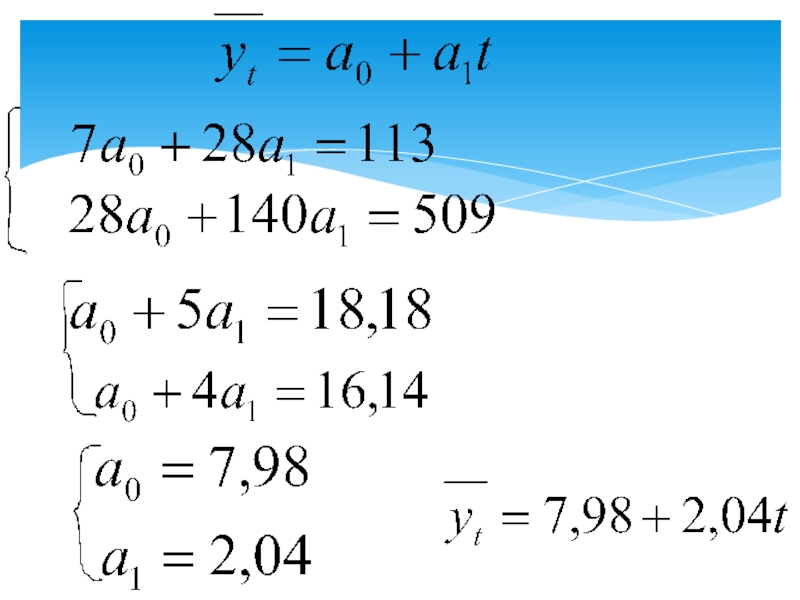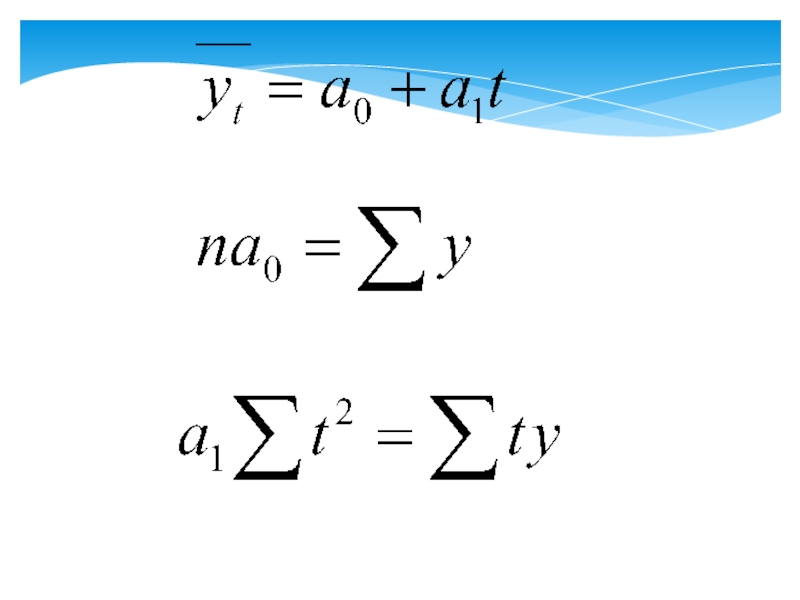- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика социально-экономических явлений презентация
Содержание
- 1. Динамика социально-экономических явлений
- 2. Ряд динамики – это временная последовательность значений конкретного статистического показателя
- 4. 1. По фактору времени: Ряды динамики бывают: - интервальные - моментные
- 5. Интервальным называется ряд динамики, уровни которого характеризуют СЭЯ за интервалы времени
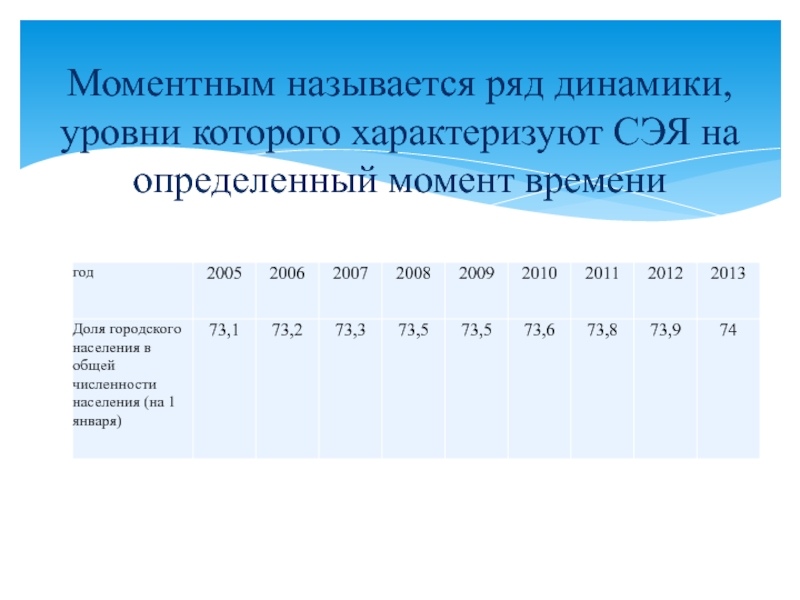
- 6. Моментным называется ряд динамики, уровни которого характеризуют СЭЯ на определенный момент времени
- 7. 2. По форме выражения уровней: Ряды динамики бывают: - абсолютные - относительные - средние
- 8. 3. По расстоянию между уровнями: Ряды динамики бывают: - равноотстоящие - не равноотстоящие
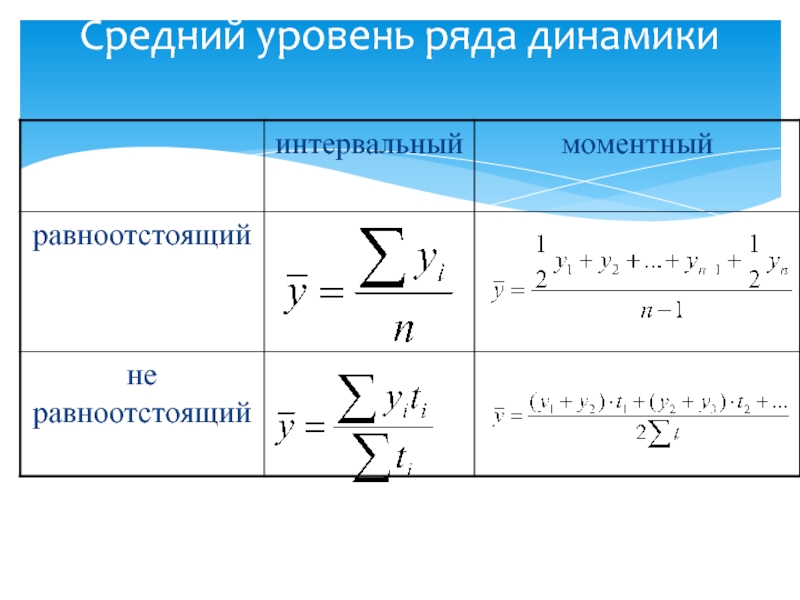
- 9. Средний уровень ряда динамики
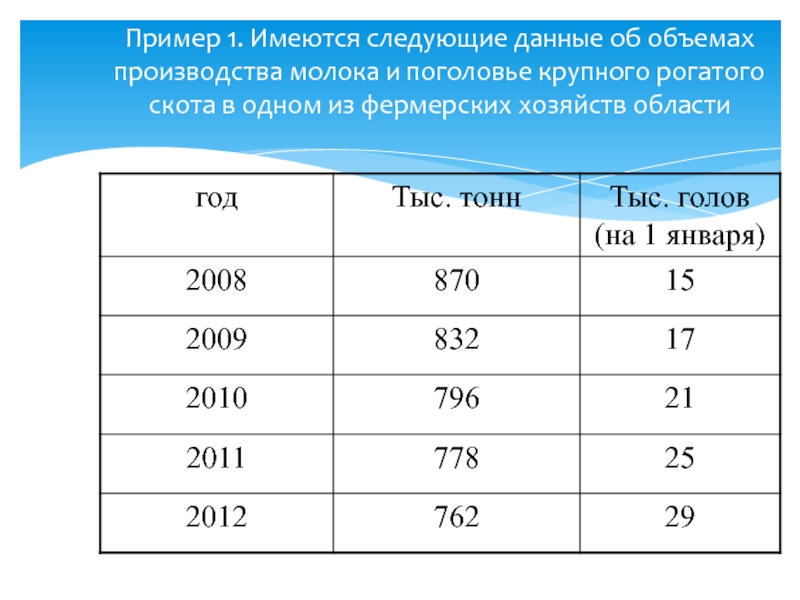
- 10. Пример 1. Имеются следующие данные об объемах
- 11. 1. 2.
- 12. Пример 1. Имеются следующие данные о поголовье
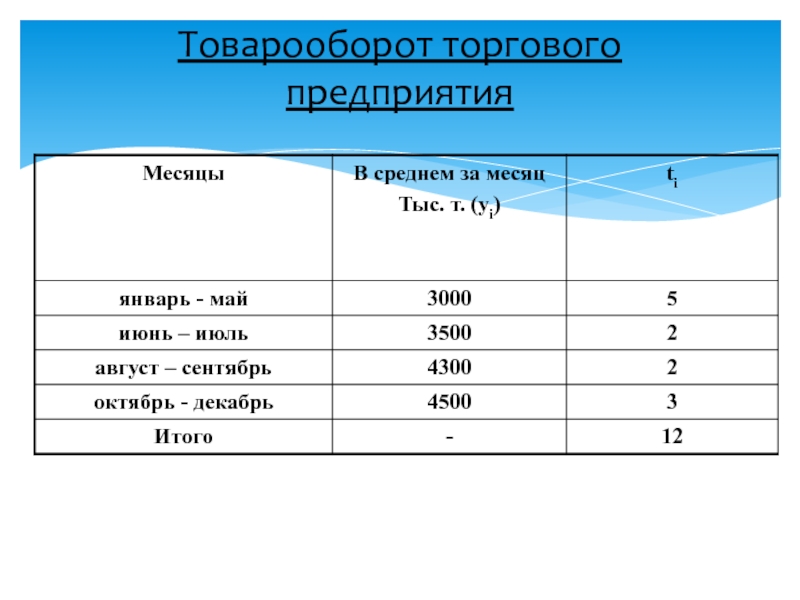
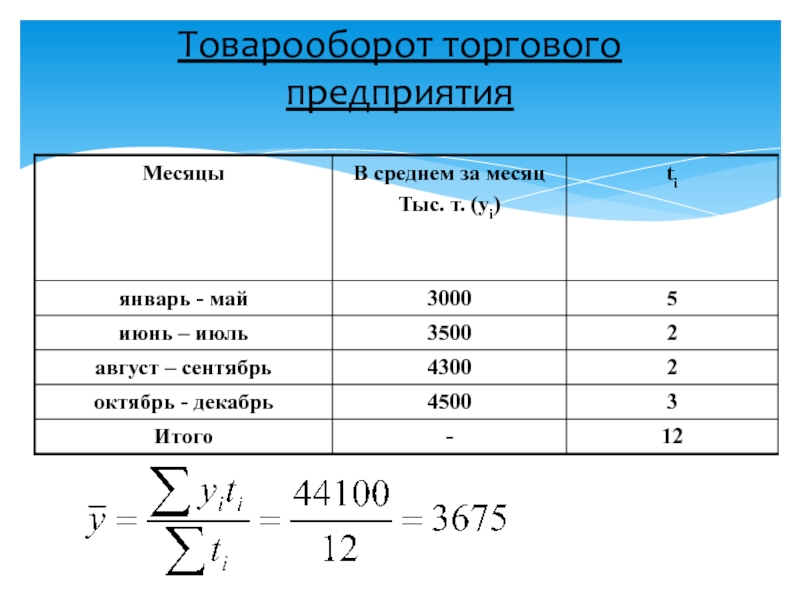
- 14. Товарооборот торгового предприятия
- 15. Товарооборот торгового предприятия
- 16. Товарооборот торгового предприятия
- 17. Абсолютный прирост Темп роста Темп прироста Абсолютное значение 1% прироста Аналитические показатели рядов динамики
- 18. Абсолютный прирост - цепной базисный - средний
- 19. Темп роста цепной базисный - средний
- 20. Темп прироста
- 21. Темп прироста цепной базисный средний
- 22. Абсолютное значение одного процента прироста
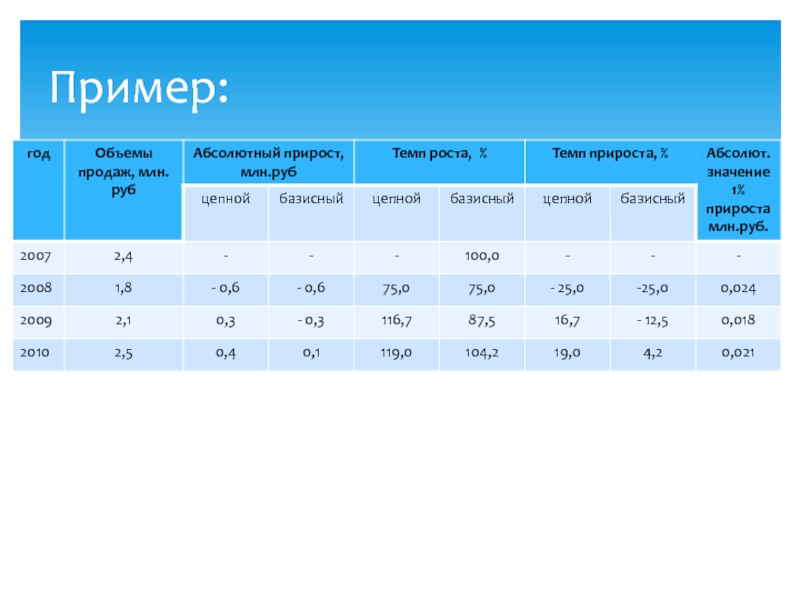
- 23. Пример:
- 25. несопоставимость по территории несопоставимость вследствие различных единиц
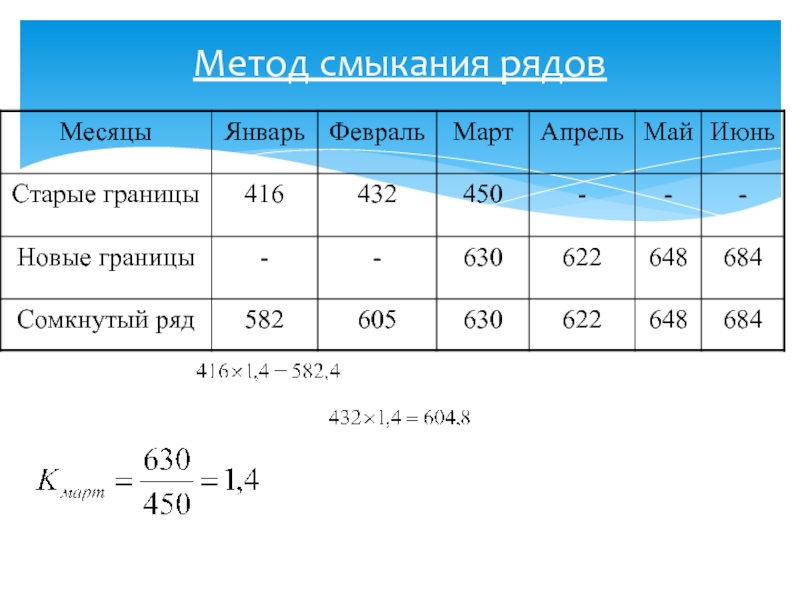
- 26. Метод смыкания рядов
- 27. Метод смыкания рядов
- 28. Метод смыкания рядов
- 29. Январь 125:150=0,822 или 82,2% Февраль 130:150=0,867 или
- 30. Статистическое изучение основной тенденции развития социально-экономического явления тренд yi t
- 31. T – основная тенденция (тренд) S –
- 32. Мультипликативная модель Yt=T*S*Е
- 33. Аддитивная модель Yt=T+S+Е
- 34. Под основной тенденцией в статистике понимают изменения
- 35. Методы выявления основной тенденции - метод скользящей средней - метод аналитического выравнивания
- 36. Исследование основной тенденции динамики методом скользящей средней
- 37. Расчет простой скользящей средней по исследуемому динамическому
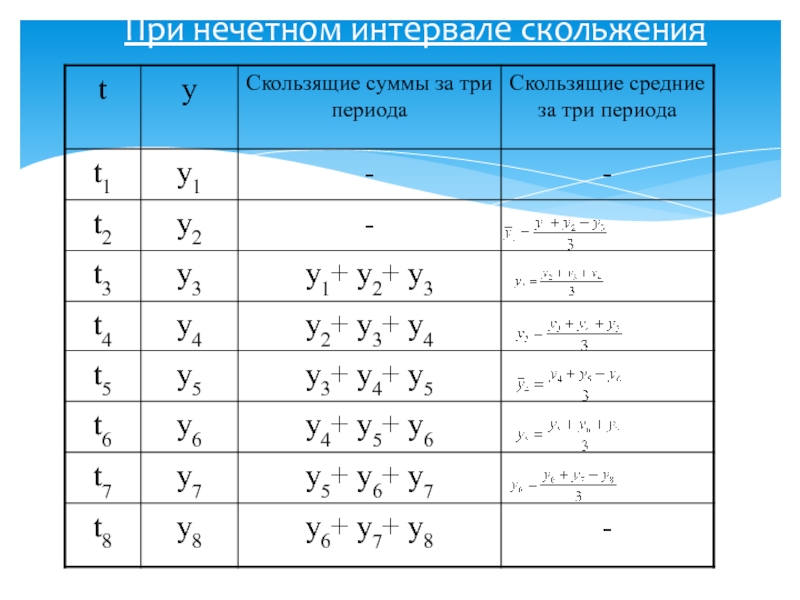
- 38. При нечетном интервале скольжения
- 39. При четном интервале скольжения
- 40. Метод скользящих средних в анализе урожайности зерновых
- 42. Условное обозначение t
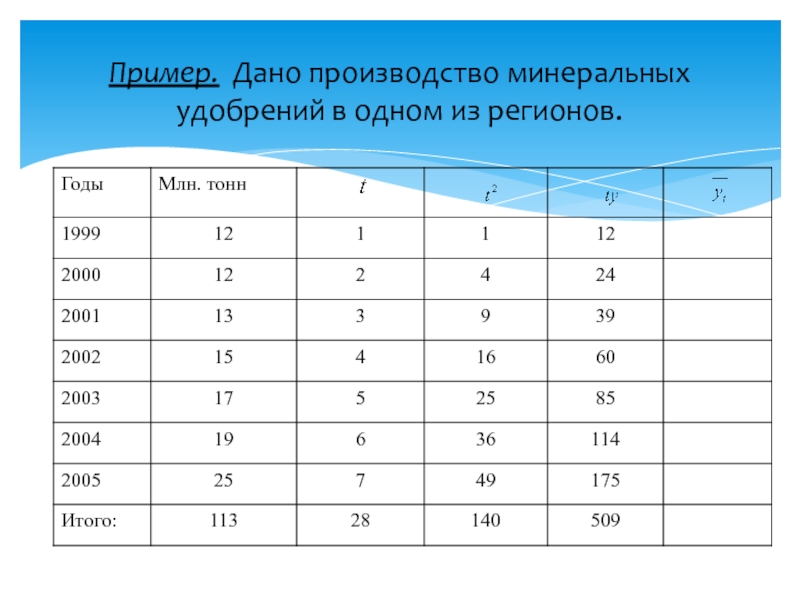
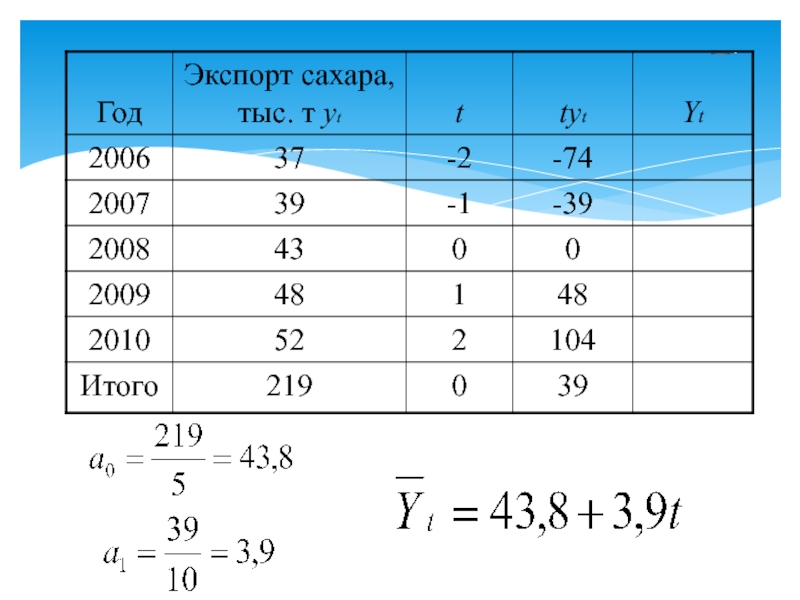
- 45. Пример. Дано производство минеральных удобрений в одном из регионов.
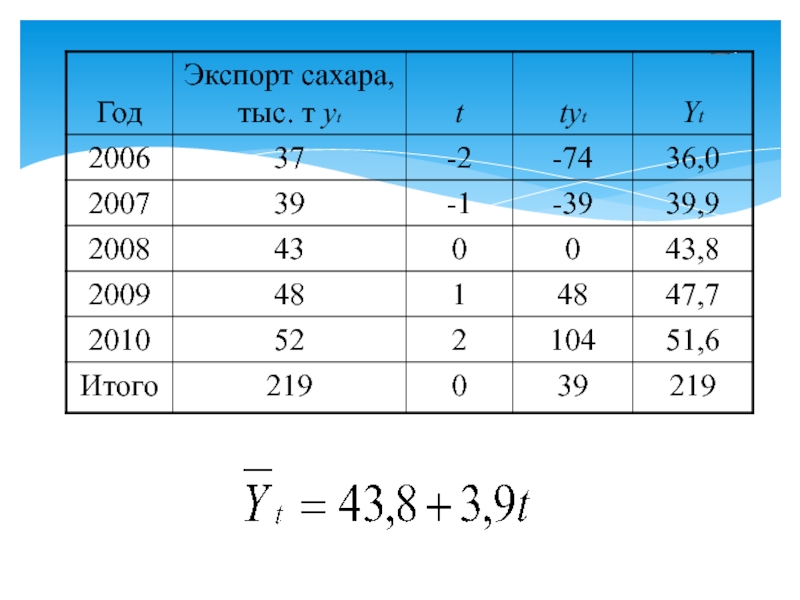
- 47. Пример. Дано производство минеральных удобрений в одном из регионов.
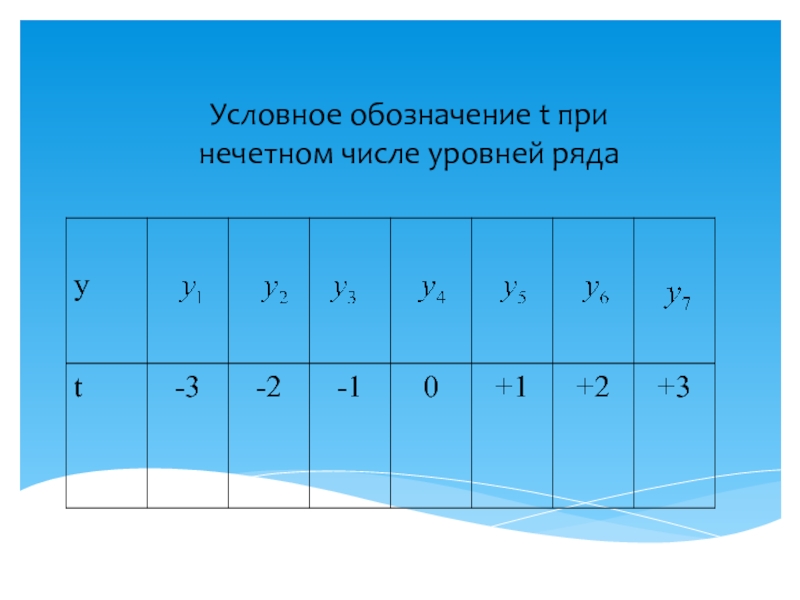
- 48. Условное обозначение t при нечетном числе уровней ряда
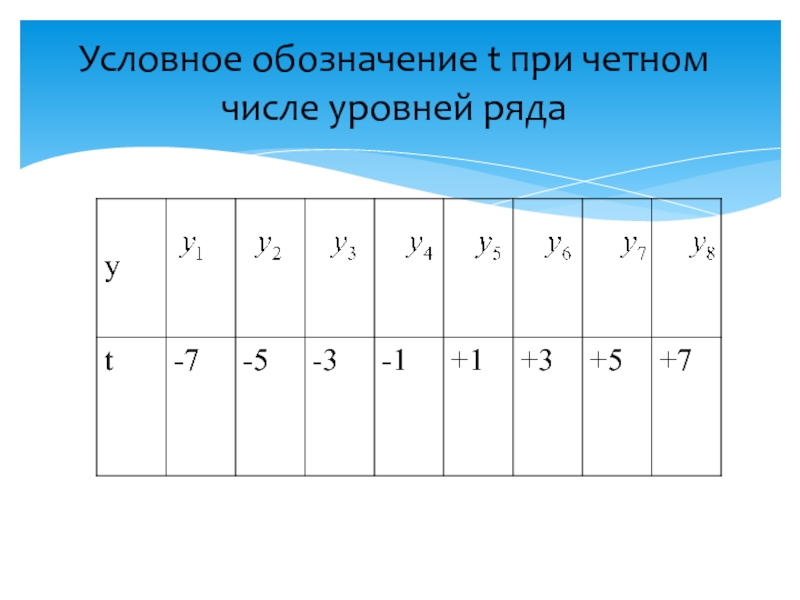
- 49. Условное обозначение t при четном числе уровней ряда
- 55. Сезонность – это колебания в уровнях ряда
- 56. Если нет основной тенденции
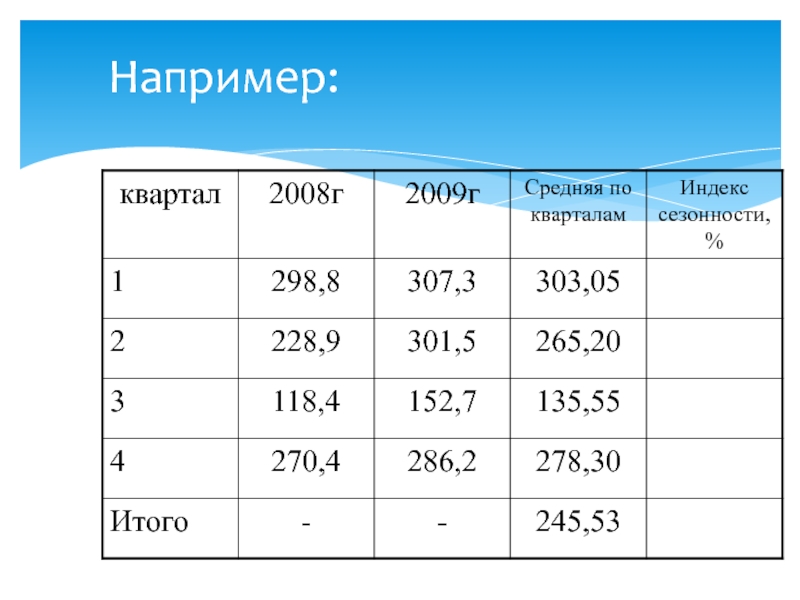
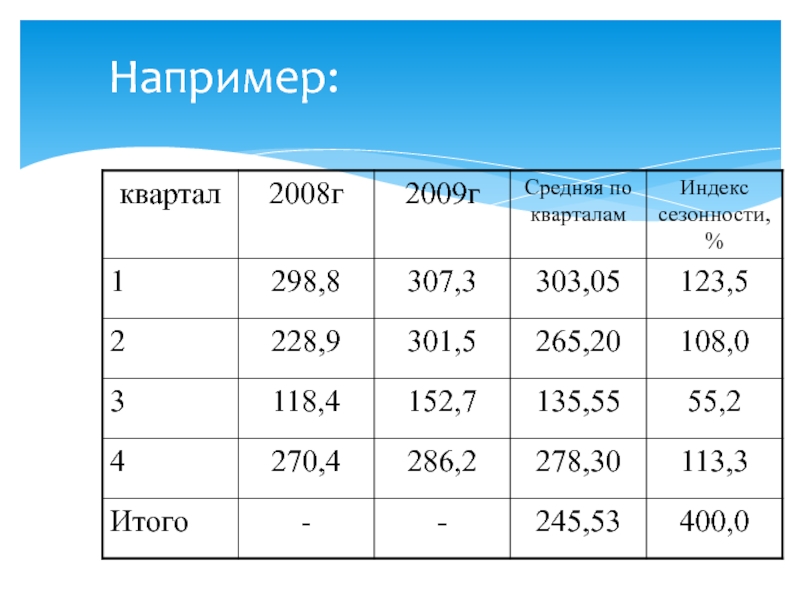
- 57. Например:
- 58. Например:
- 59. Ряди динамики с тенденцией
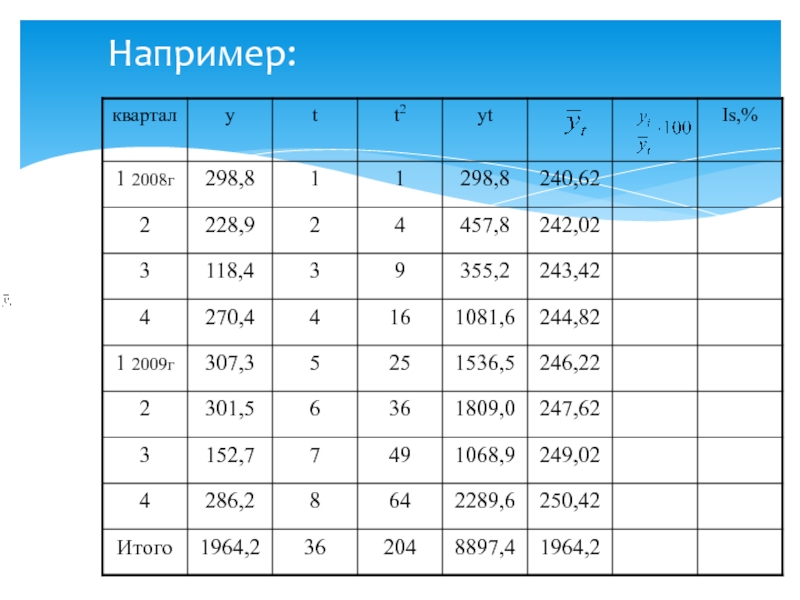
- 60. Например:
- 61. Например:
- 62. yt = a0 + Σ(ak cos kt
- 63. Гармоника Фурье
- 64. k=1: yt =
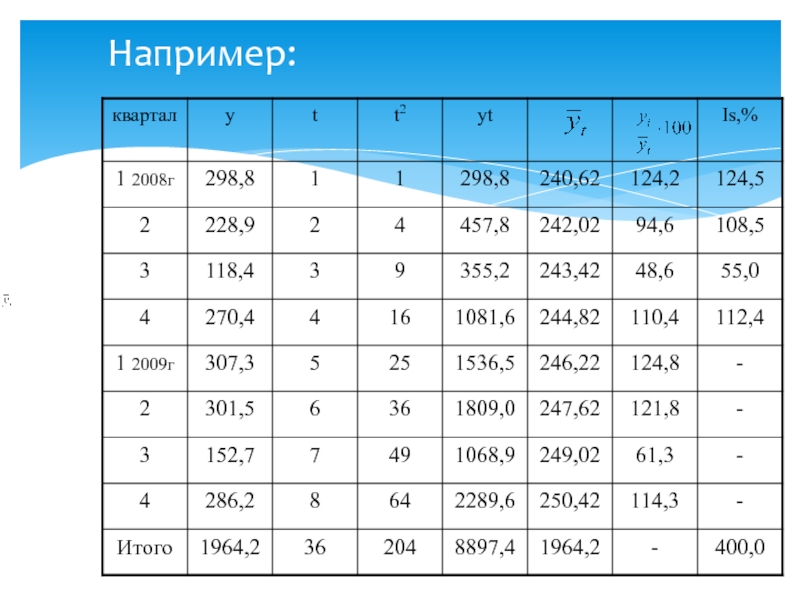
- 65. Например:
Ряд динамики – это временная последовательность значений конкретного статистического показателя
Слайд 2Ряд динамики – это временная последовательность значений конкретного статистического показателя
Слайд 6Моментным называется ряд динамики, уровни которого характеризуют СЭЯ на определенный момент
времени
Слайд 10Пример 1. Имеются следующие данные об объемах производства молока и поголовье
крупного рогатого скота в одном из фермерских хозяйств области
Слайд 12Пример 1. Имеются следующие данные о поголовье крупного рогатого скота в
одном из фермерских хозяйств области
Слайд 17Абсолютный прирост
Темп роста
Темп прироста
Абсолютное значение 1% прироста
Аналитические показатели рядов динамики
Слайд 25несопоставимость по территории
несопоставимость вследствие различных единиц измерения и единиц счета
Несопоставимость по
методологии учета или расчета показателей
Несопоставимость по кругу охватываемых объектов
Несопоставимость по кругу охватываемых объектов
Несопоставимость уровней рядов динамики
Слайд 29Январь 125:150=0,822 или 82,2%
Февраль 130:150=0,867 или 86,7%
Март – 100%
Апрель 175:170=1,029 или
102,9%
Май 180:170=1,059 или 105,9%
Май 180:170=1,059 или 105,9%
Слайд 30Статистическое изучение основной тенденции развития социально-экономического явления
тренд
yi
t
Слайд 31T – основная тенденция (тренд)
S – сезонная составляющая (циклическая)
Е – случайная
компонента
Компоненты ряда динамики
Слайд 34Под основной тенденцией в статистике понимают изменения в уровнях ряда динамики,
определяющие направление развития явления во времени во времени
Слайд 35Методы выявления основной тенденции
- метод скользящей средней
- метод аналитического выравнивания
Слайд 36 Исследование основной тенденции динамики методом скользящей средней
Общая формула скользящей средней
где: МА
– скользящая средняя (от англ. – moving average);
k – порядок скользящей средней, т. е. число уровней, входящих в интервал сглаживания;
уi – i-й уровень ряда динамики;
k – порядок скользящей средней, т. е. число уровней, входящих в интервал сглаживания;
уi – i-й уровень ряда динамики;
Слайд 37 Расчет простой скользящей средней по исследуемому динамическому ряду, состоящему из n
уровней включает следующие этапы:
1. Выбирается период осреднения (k).
2. Вычисляется сумма первых k уровней.
3. Делением данной суммы на k получается скользящая средняя.
4. Из рассчитанной в п.2 суммы вычитается первый уровень и прибавляется следующий за интервалом осреднения уровень динамического ряда.
5. Этапы 3 и 4 повторяются до исчерпания всех уровней.
Рассмотрим пример вычисления простой скользящей средней.
1. Выбирается период осреднения (k).
2. Вычисляется сумма первых k уровней.
3. Делением данной суммы на k получается скользящая средняя.
4. Из рассчитанной в п.2 суммы вычитается первый уровень и прибавляется следующий за интервалом осреднения уровень динамического ряда.
5. Этапы 3 и 4 повторяются до исчерпания всех уровней.
Рассмотрим пример вычисления простой скользящей средней.
Слайд 40Метод скользящих средних в анализе урожайности зерновых культур в РФ (в хозяйствах
всех категорий; ц с 1 га)
Слайд 55Сезонность – это колебания в уровнях ряда динамики периодически повторяющиеся в
определенное время каждого года, месяца, дня.
Методы изучения сезонной компоненты
Слайд 62yt = a0 + Σ(ak cos kt + bk sin kt)
где:
k – определяет номер гармоники ряда Фурье и может быть взята с разной степенью точности (чаще от «1» до «4»).
Гармоника Фурье
Слайд 64k=1: yt = a0 + a1 cos
t + b1 sin t ;
k=2:
yt = a0 + a1 cos t + b1 sin t + a2 cos 2t + +b2 sin 2t
k = 3
yt = a0+a1cost+b1sint+a2cos2t+b2sin2t+
+a3cos3t + b3sin3t
k=2:
yt = a0 + a1 cos t + b1 sin t + a2 cos 2t + +b2 sin 2t
k = 3
yt = a0+a1cost+b1sint+a2cos2t+b2sin2t+
+a3cos3t + b3sin3t
Гармоники Фурье
