- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритм оценки запаса промысловой части популяции рыб презентация
Содержание
- 1. Алгоритм оценки запаса промысловой части популяции рыб
- 2. ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ РАСЧЕТА ЗАПАСА ПРОМЫСЛОВОЙ ЧАСТИ ПОПУЛЯЦИИ
- 3. 4. Коэффициенты смертности рыб:
- 4. 5. Оценка уровня эксплуатации промысловой части
- 5. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ МЕЖДУ ДЛИНОЙ
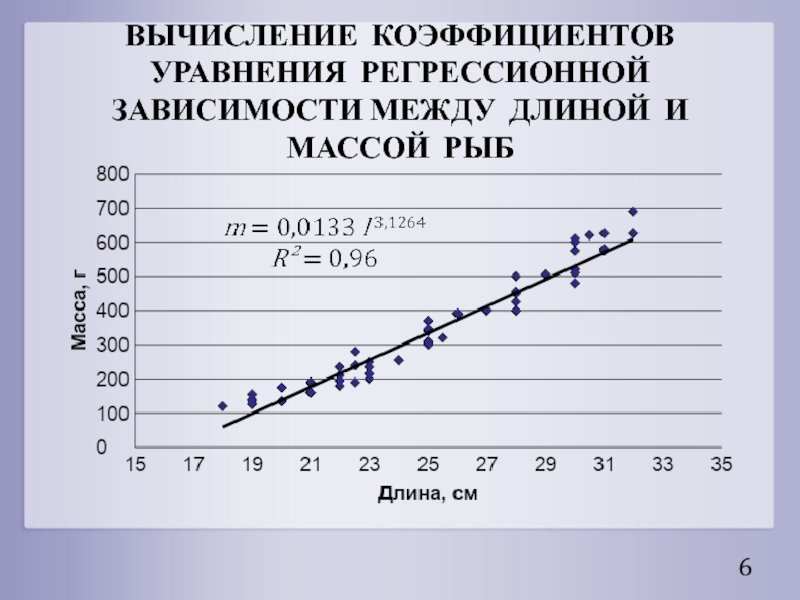
- 6. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ МЕЖДУ ДЛИНОЙ И МАССОЙ РЫБ
- 7. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ МЕЖДУ ДЛИНОЙ
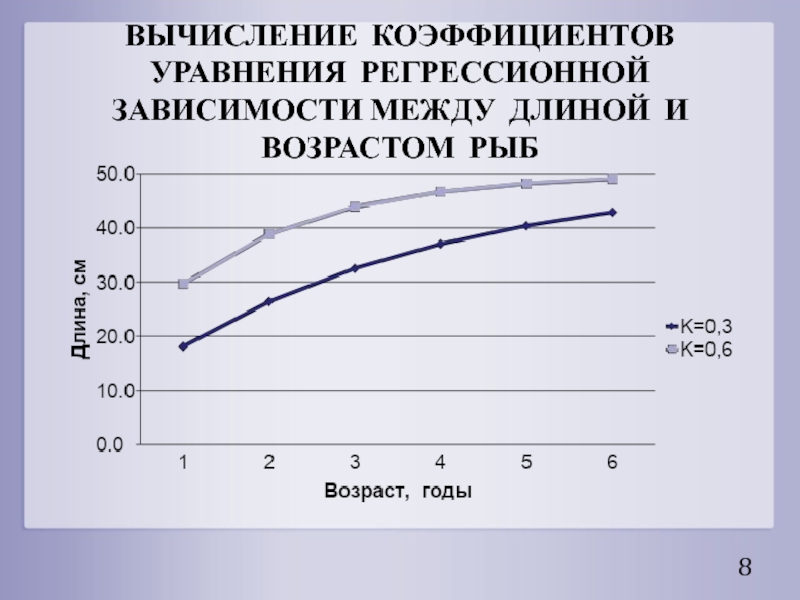
- 8. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ МЕЖДУ ДЛИНОЙ И ВОЗРАСТОМ РЫБ
- 9. РАСЧЕТ ВЕЛИЧИН ПОКАЗАТЕЛЕЙ СКОРОСТИ РОСТА МАССЫ (Ф)
- 10. ОЦЕНКА ОБЩЕЙ СМЕРТНОСТИ НА ОСНОВЕ ВОЗРАСТНОЙ СТРУКТУРЫ
- 11. ОЦЕНКА ЕСТЕСТВЕННОЙ СМЕРТНОСТИ ПОПУЛЯЦИИ РЫБ
- 12. ОЦЕНКА ПРОМЫСЛОВОЙ СМЕРТНОСТИ ПОПУЛЯЦИИ РЫБ Промысловая смертность
- 13. ОЦЕНКА УРОВНЯ ЭКСПЛУАТАЦИИ ПРОМЫСЛОВОЙ ЧАСТИ ПОПУЛЯЦИИ РЫБ
- 14. ОЦЕНКА БИОМАССЫ ПРОМЫСЛОВОЙ ЧАСТИ ПОПУЛЯЦИИ РЫБ
- 15. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ ДЛИНЫ РЫБ ДЛЯ
- 16. РАСЧЕТ ОТНОСИТЕЛЬНОГО ПОКАЗАТЕЛЯ ПРОДУКТИВНОСТИ ПРОМЫСЛОВОЙ ЧАСТИ ПОПУЛЯЦИИ
- 17. РАСЧЕТ ОТНОСИТЕЛЬНОГО ПОКАЗАТЕЛЯ ПРОДУКТИВНОСТИ ПРОМЫСЛОВОЙ ЧАСТИ ПОПУЛЯЦИИ
- 18. БЛАГОДАРИМ ЗА ВНИМАНИЕ
ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ РАСЧЕТА ЗАПАСА ПРОМЫСЛОВОЙ
ЧАСТИ ПОПУЛЯЦИИ РЫБ 1. Вычисление коэффициентов уравнения регрессионной зависимости между длиной и массой рыб;
2. Вычисление коэффициентов уравнения регрессионной зависимости между длиной и возрастом рыб;
Слайд 2ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ РАСЧЕТА ЗАПАСА ПРОМЫСЛОВОЙ
ЧАСТИ ПОПУЛЯЦИИ РЫБ
1. Вычисление коэффициентов уравнения регрессионной
зависимости между длиной и массой рыб;
2. Вычисление коэффициентов уравнения регрессионной зависимости между длиной и возрастом рыб;
3. Расчет величин показателей скорости роста массы и длины рыб;
Слайд 3
4. Коэффициенты смертности рыб:
4.1. Оценка общей смертности на основе
возрастной структуры популяции;
4.2. Оценка естественной смертности популяции рыб; 4.3. Оценка промысловой смертности популяции рыб;
4.2. Оценка естественной смертности популяции рыб; 4.3. Оценка промысловой смертности популяции рыб;
Слайд 4
5. Оценка уровня эксплуатации промысловой части популяции рыб;
6. Оценка биомассы промысловой
части популяции рыб;
7. Определение оптимальной длины рыб для промысла; 8. Расчет относительного показателя продуктивности промысловой части популяции рыб.
7. Определение оптимальной длины рыб для промысла; 8. Расчет относительного показателя продуктивности промысловой части популяции рыб.
Слайд 5ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ МЕЖДУ ДЛИНОЙ И МАССОЙ РЫБ
Дж. Гексли
[1922]
где m и l – это масса и длина рыбы, а параметры a и b зависят от вида рыбы и среды обитания.
где m и l – это масса и длина рыбы, а параметры a и b зависят от вида рыбы и среды обитания.
Слайд 7ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ МЕЖДУ ДЛИНОЙ И ВОЗРАСТОМ РЫБ
К. Л.
фон Берталанфи [1938]
где l – длина рыбы, t – возраст рыбы,
L∞ – асимптотическая длина рыбы,
K – параметр, характеризующий темп роста, t0 – условное значение возраста, в котором длина рыбы равна нулю.
где l – длина рыбы, t – возраст рыбы,
L∞ – асимптотическая длина рыбы,
K – параметр, характеризующий темп роста, t0 – условное значение возраста, в котором длина рыбы равна нулю.
Слайд 9РАСЧЕТ ВЕЛИЧИН ПОКАЗАТЕЛЕЙ СКОРОСТИ РОСТА МАССЫ (Ф) И ДЛИНЫ (Ф’) РЫБ
Ж.
Л. Мунро и Д. Паули [1983]
где величины коэффициентов K и L∞ берутся из уравнения Берталанфи, а m∞ находится через уравнение Гексли.
где величины коэффициентов K и L∞ берутся из уравнения Берталанфи, а m∞ находится через уравнение Гексли.
Слайд 10ОЦЕНКА ОБЩЕЙ СМЕРТНОСТИ НА ОСНОВЕ
ВОЗРАСТНОЙ СТРУКТУРЫ ПОПУЛЯЦИИ
Общая смертность – характеризуется годовым
(φZ) и мгновенным (Z) коэффициентами:
где n – число возрастных групп, а Nt – количество экземпляров в возрасте t.
где n – число возрастных групп, а Nt – количество экземпляров в возрасте t.
Слайд 11
ОЦЕНКА ЕСТЕСТВЕННОЙ
СМЕРТНОСТИ ПОПУЛЯЦИИ РЫБ
Естественная смертность – годовой (φM) и мгновенный (M)
коэффициенты [Паули, 1980] :
где T – среднегодовая температура водоема, а K и L∞ берутся из уравнения Берталанфи.
где T – среднегодовая температура водоема, а K и L∞ берутся из уравнения Берталанфи.
Слайд 12ОЦЕНКА ПРОМЫСЛОВОЙ
СМЕРТНОСТИ ПОПУЛЯЦИИ РЫБ
Промысловая смертность – характеризуется годовым (φF) и мгновенным
(F) коэффициентами [Засосов, 1970] :
Слайд 13ОЦЕНКА УРОВНЯ ЭКСПЛУАТАЦИИ ПРОМЫСЛОВОЙ ЧАСТИ ПОПУЛЯЦИИ РЫБ
Р. Дж. Х. Бивертон и
С. Дж. Холт [1966]
где F и Z – мгновенные коэффициенты промысловой и общей смертности.
где F и Z – мгновенные коэффициенты промысловой и общей смертности.
Слайд 14ОЦЕНКА БИОМАССЫ ПРОМЫСЛОВОЙ
ЧАСТИ ПОПУЛЯЦИИ РЫБ
Р. Дж. Х. Бивертон и
С. Дж. Холт [1966]
где C – величина улова, а U – уровень эксплуатации.
Максимально допустимый улов
Ж.-П. Троадек [1977] (формула Кадимы):
где C – величина улова, а U – уровень эксплуатации.
Максимально допустимый улов
Ж.-П. Троадек [1977] (формула Кадимы):
Слайд 15
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ
ДЛИНЫ РЫБ ДЛЯ ПРОМЫСЛА
Р. Дж. Х. Бивертон [1992]
где величины коэффициентов K и L∞ берутся из уравнения Берталанфи, а M – мгновенный коэффициент естественной смертности.
Слайд 16РАСЧЕТ ОТНОСИТЕЛЬНОГО ПОКАЗАТЕЛЯ ПРОДУКТИВНОСТИ ПРОМЫСЛОВОЙ
ЧАСТИ ПОПУЛЯЦИИ РЫБ
Р. Дж. Х. Бивертон
и С. Дж. Холт [1966]
где lc – длина рыб, начиная с которой они входят в промысловую часть популяции.
где lc – длина рыб, начиная с которой они входят в промысловую часть популяции.
