- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кривые размножения и жизненные таблицы (life tables) презентация
Содержание
- 1. Кривые размножения и жизненные таблицы (life tables)
- 2. Мы вновь возвращаемся к формированию возрастной структуры
- 3. Кривая размножения – удельная скорость размножения (или
- 4. Кривые размножения: примеры (1) Мятлик однолетний Poa
- 5. Кривые размножения: примеры (2) Вошь Pediculus humanus
- 6. Кривые размножения: примеры (3) Среднее число яиц
- 7. (1) Однократное размножение на протяжении жизни (semelparity,
- 8. Жизненная таблица и связанные с ней понятия
- 9. Какой смысл имеет чистая скорость воспроизводства R0?
- 10. Какой смысл имеет чистая скорость воспроизводства R0?
- 11. Среднее время генерации G – это средний
- 12. Понятно ли, что среднее (оно же «средневзвешенное»,
- 13. Механическая модель для определения длительности поколения* (1)
- 14. Тот факт, что балансир находится в равновесии,
- 15. Приближённый способ расчета удельной скорости роста численности
- 16. R0 - безразмерная величина, которая показывает,
- 17. Кому давать орден «Мать-героиня»? Из лекций А.М. Гилярова
- 18. Популяция, где по пять детей у молодых
- 19. r1 = (ln 2.5) / 20 =
- 20. Мы вновь возвращаемся к жизненной таблице. Теперь
- 21. Параметры, которые вводятся на следующих слайдах n0(t),
- 22. Как формируется численность популяции и отдельных возрастных
- 23. Как формируется численность популяции и отдельных возрастных
- 24. Экспоненциальный рост общей численности популяции (см. λ
- 25. Теорема Лотки Alfred James Lotka (1880-1949) Фото:
- 26. Из лекций А.М. Гилярова
- 27. Матрицы Лесли (Paul H. Leslie, британский эколог):
- 28. Для тех, кто знаком с основными понятиями
- 29. Значение теоремы Лотки Иногда полагают, что в
- 30. Фундаментальное значение роста в геометрической прогрессии “Geometrical
- 31. Вслед за Дарвином считаем слонов … ☺
- 32. – количество родившихся
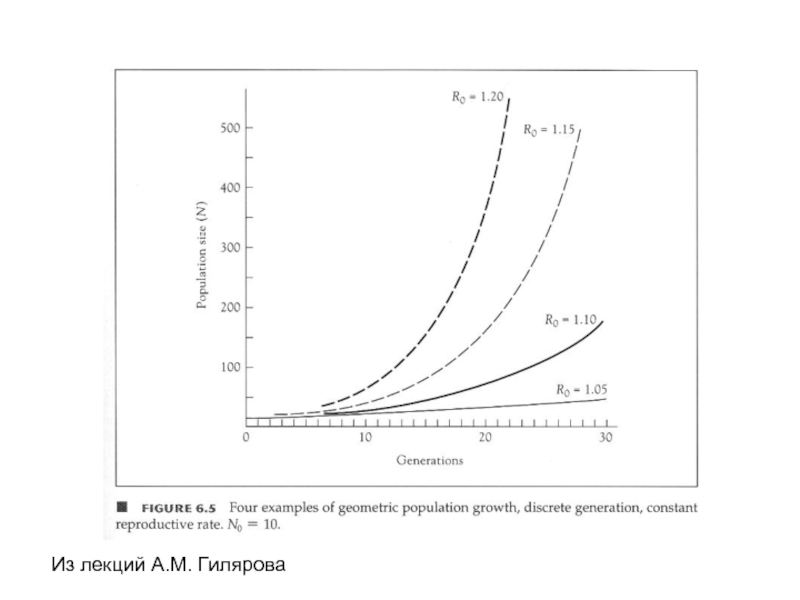
- 33. Расчет удельной скорости роста численности r по
- 34. Как найти r из уравнения Эйлера-Лотки?
- 35. Решение уравнения Эйлера-Лотки в пакете Excel (1)
- 36. Решение уравнения Эйлера-Лотки в пакете Excel (2)
- 37. Сумма в левой части уравнения Эйлера-Лотки приняла
- 38. Пример расчета r по формуле Эйлера-Лотки, или
- 39. IUCN Red List - Международная Красная книга
- 40. Расчет r (точнее, λ) по Russel Lande
- 41. Преобразование уравнения Эйлера-Лотки (продолжение)
- 42. Демографические характеристики пятнистой неясыти (по Lande 1988)
- 43. Расчет коэффициента роста численности λ для пятнистой
- 44. Вызов команды «Поиск решения» и задание в
- 45. Сумма в левой части уравнения для λ
- 46. Заключение При указанных значениях демографических параметров пятнистая
- 47. Согласно теореме Лотки (см. также рассмотренный выше
- 48. Возрастное распределение Homo sapiens, 1970 г.
- 49. Разгадка: Возрастное распределение Homo sapiens, 1970 г.
- 50. Возрастное распределение народонаселения Франции на 1
- 51. Возрастное распределение народонаселения России на
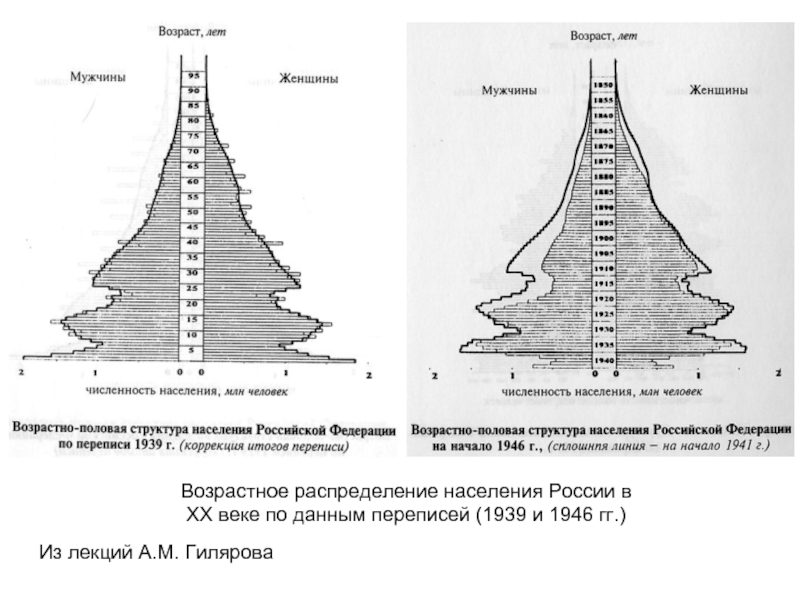
- 52. Из лекций А.М. Гилярова Возрастное распределение населения
- 53. Из лекций А.М. Гилярова Возрастное распределение населения
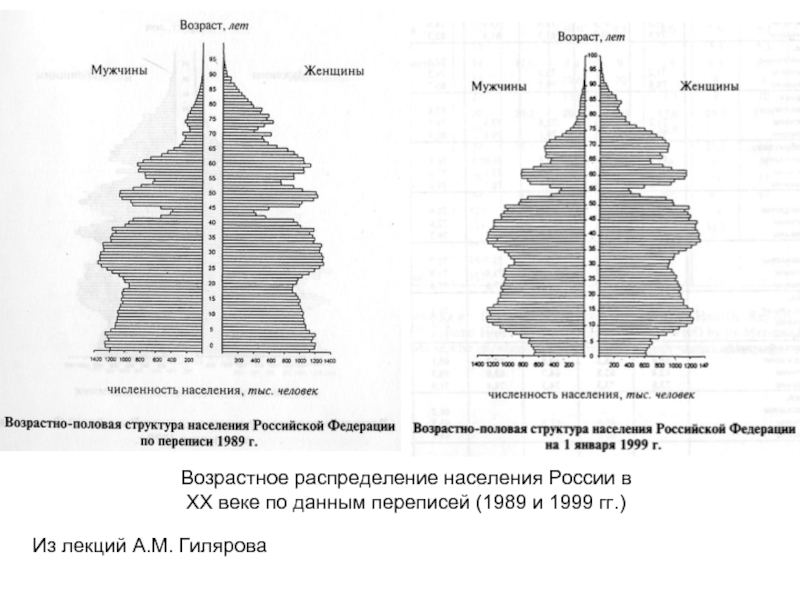
- 54. Из лекций А.М. Гилярова Возрастное распределение населения
- 55. Из лекций А.М. Гилярова Возрастное распределение населения
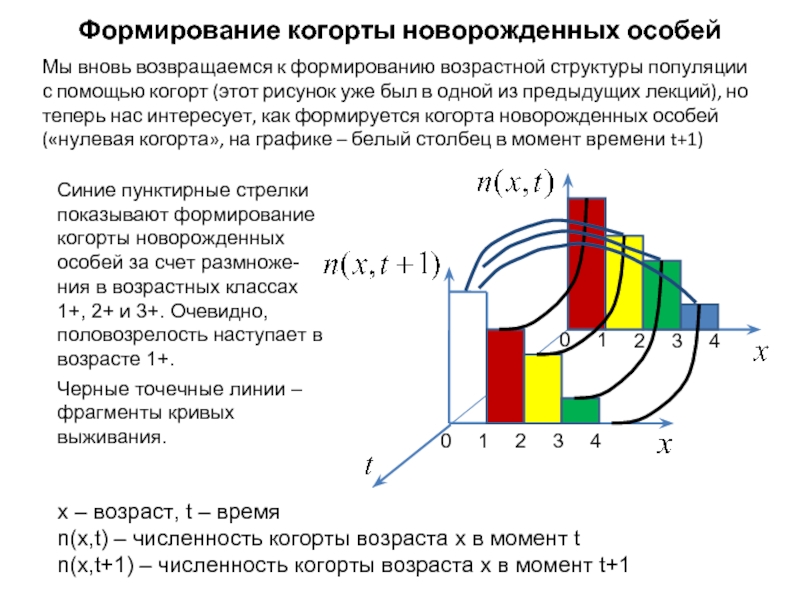
Слайд 2Мы вновь возвращаемся к формированию возрастной структуры популяции с помощью когорт
x – возраст, t – время
n(x,t) – численность когорты возраста x в момент t
n(x,t+1) – численность когорты возраста x в момент t+1
Синие пунктирные стрелки показывают формирование когорты новорожденных особей за счет размноже-ния в возрастных классах
1+, 2+ и 3+. Очевидно, половозрелость наступает в возрасте 1+.
Черные точечные линии – фрагменты кривых выживания.
1
2
3
4
0
1
0
2
3
4
Формирование когорты новорожденных особей
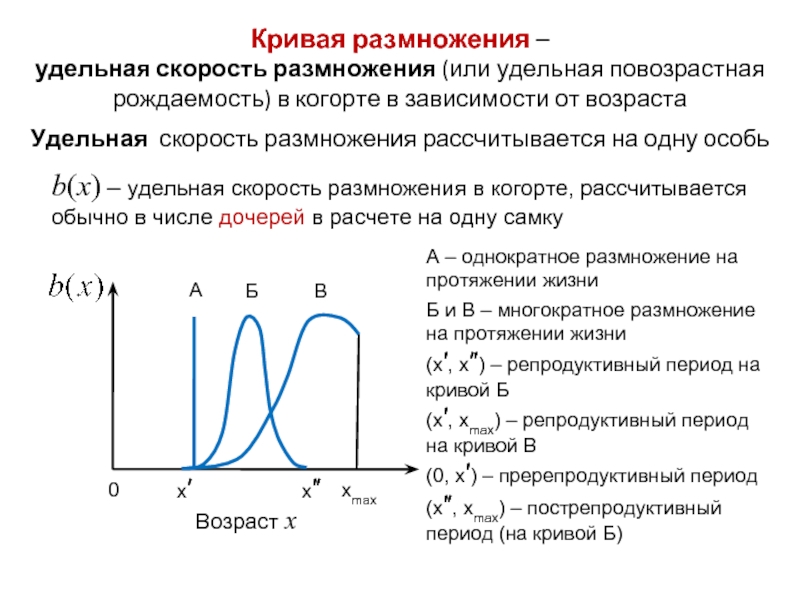
Слайд 3Кривая размножения –
удельная скорость размножения (или удельная повозрастная рождаемость) в когорте
Удельная скорость размножения рассчитывается на одну особь
Возраст x
xmax
0
x′
x″
Б
В
А – однократное размножение на протяжении жизни
Б и В – многократное размножение на протяжении жизни
(x′, x″) – репродуктивный период на кривой Б
(x′, xmax) – репродуктивный период на кривой В
(0, x′) – пререпродуктивный период
(x″, xmax) – пострепродуктивный период (на кривой Б)
А
b(x) – удельная скорость размножения в когорте, рассчитывается обычно в числе дочерей в расчете на одну самку
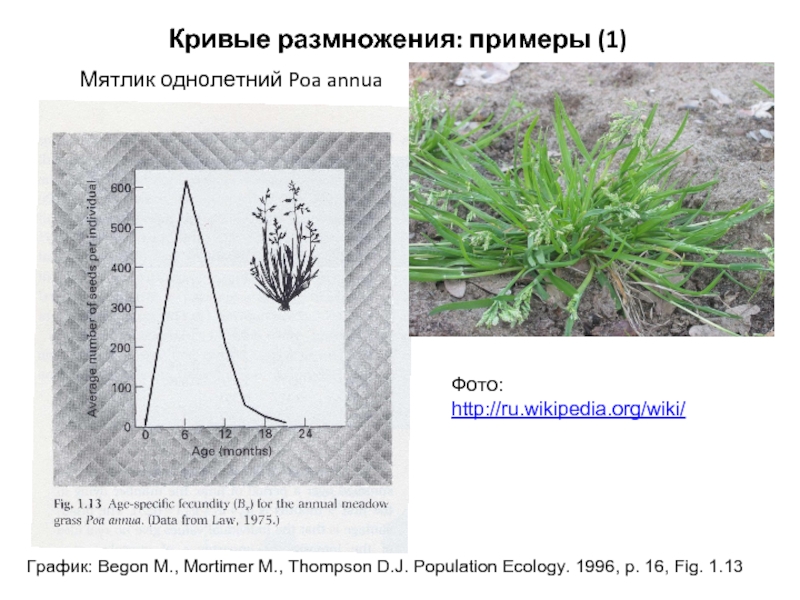
Слайд 4Кривые размножения: примеры (1)
Мятлик однолетний Poa annua
Фото: http://ru.wikipedia.org/wiki/
График: Begon M., Mortimer
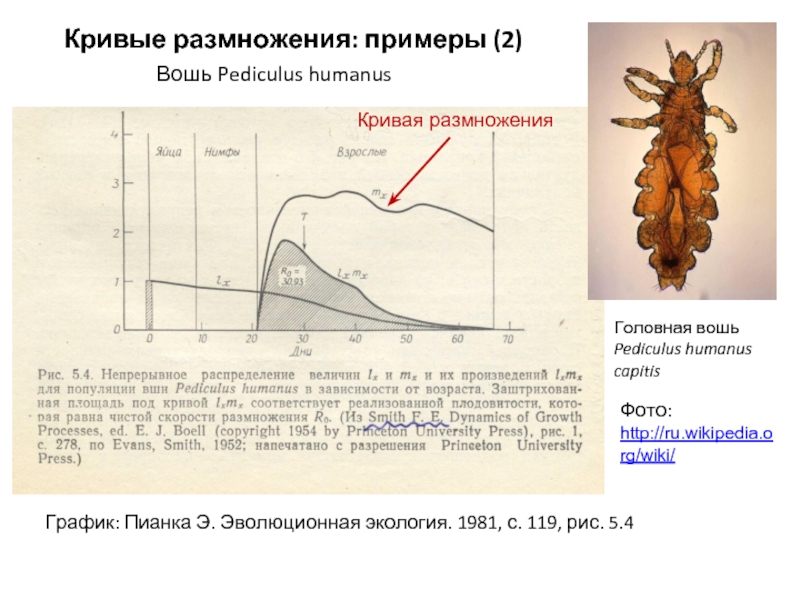
Слайд 5Кривые размножения: примеры (2)
Вошь Pediculus humanus
Головная вошь Pediculus humanus capitis
Кривая размножения
Фото:
График: Пианка Э. Эволюционная экология. 1981, с. 119, рис. 5.4
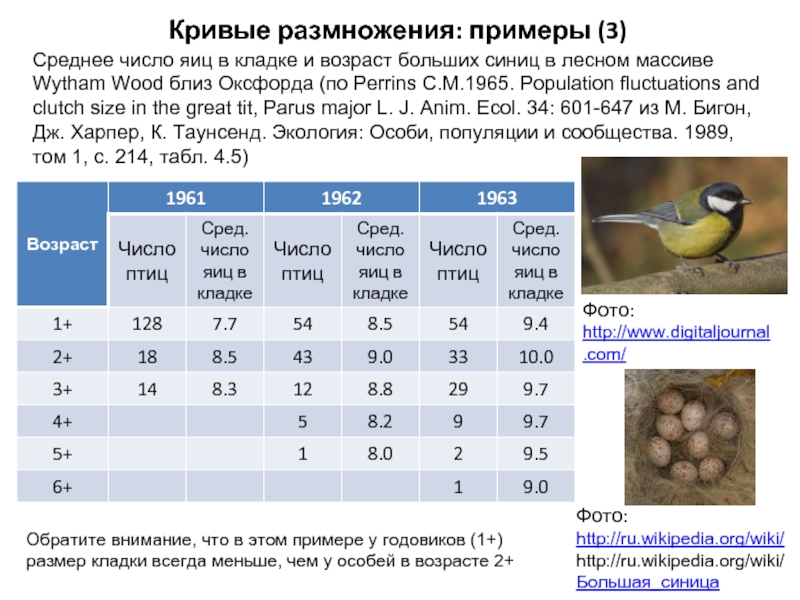
Слайд 6Кривые размножения: примеры (3)
Среднее число яиц в кладке и возраст больших
Обратите внимание, что в этом примере у годовиков (1+) размер кладки всегда меньше, чем у особей в возрасте 2+
Фото:
http://www.digitaljournal.com/
Фото:
http://ru.wikipedia.org/wiki/http://ru.wikipedia.org/wiki/Большая_синица
Слайд 7(1) Однократное размножение на протяжении жизни (semelparity, big-bang reproduction). Типичные r-стратеги
Примеры:
Две стратегии размножения
(2) Многократное размножение на протяжении жизни (iteroparity). Относительно организмов с однократным размножением такие организмы являются K-стратегами. Наблюдается у большинства организмов. (Однако вспомните пример с дафниями в 4-й лекции, когда при недостатке пищи они вели себя как K-стратеги (вкладывали ресурсы в основном в соматическую массу, т.е. в поддержание жизнедеятельности), а при избытке пищи – как r-стратеги (вкладывали ресурсы в размножение.))
Фото: http://en.wikipedia.org
Горох
Поденка Caenis horaria
(Ephemeroptera)
Чавыча (king salmon)
Oncorhynchus tschawytscha
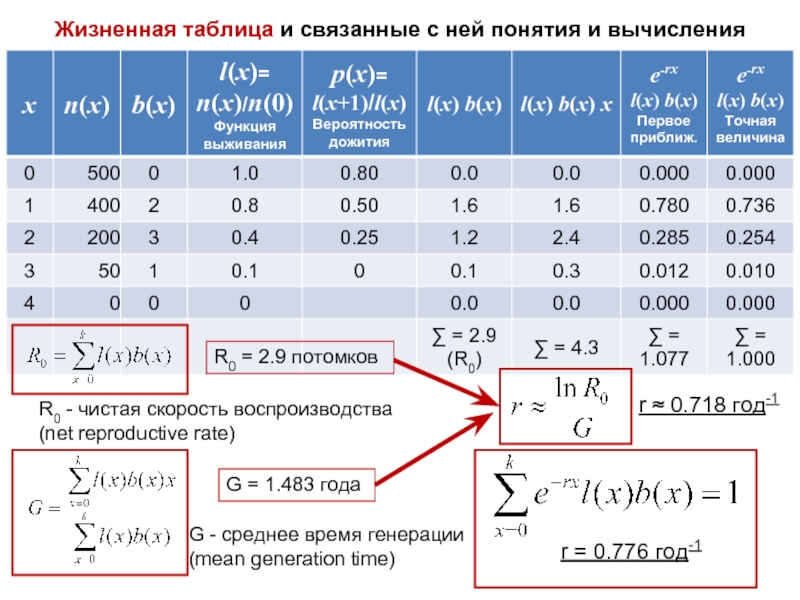
Слайд 8Жизненная таблица и связанные с ней понятия и вычисления
R0 = 2.9
G = 1.483 года
r ≈ 0.718 год-1
r = 0.776 год-1
R0 - чистая скорость воспроизводства (net reproductive rate)
G - среднее время генерации (mean generation time)
Слайд 9Какой смысл имеет чистая скорость воспроизводства R0? (1)
R0 – это
Для выяснения смысла какого-то выражения, чтобы выяснить его основное содержание, бывает полезно его несколько «огрубить» или упростить
Слайд 10Какой смысл имеет чистая скорость воспроизводства R0? (2)
Упростим выражение для
(3)
(1)
(2)
Примем, что b(x) = b – это средняя удельная рождаемость по всем возрастам (тогда ее можно вынести за знак суммы в формуле (1))
a – возраст достижения половой зрелости (на нижнем пределе суммы и в индексах),
la – доля особей, доживших до возраста a
∑l(x) в формуле (2) – это площадь под кривой выживания, а эта площадь, как мы знаем из лекции 8, делённая на la, равна средней продолжитель-ности жизни после достижения возраста a, Ta. Поэтому ∑l(x) в (2) равна Ta ∙la в (3).
Уравнение (3) показывает, что
R0 – это то количество потомков, которые произведены самкой за время ее жизни (b∙Ta) и дожили до следующего периода размножения (b∙Ta∙la)
Слайд 11Среднее время генерации G – это средний возраст размножения, т.е. средний
Что означает среднее время генерации G?
Это видно из формулы для G:
Доля особей, родившихся в возрасте x, от общего числа
особей R0, произведен-ных за
время жизни
Таким образом, сумма
то есть G представляет собой средневзвешенный возраст размножения, где «вес» возраста определяется долей произведенных в этом возрасте потомков
Слайд 12Понятно ли, что среднее (оно же «средневзвешенное», хотя это слово является
Среднее значение
Отдельные значения случайной величины
Частоты (или «веса») этих отдельных значений; сумма «весов» равна 1
Если непонятно, решите следующую школьную задачку: Найти среднее значение скорости пешехода, если ½ времени он шел со скоростью 10 км/час (видимо, бежал, торопился на лекцию ☺), ¼ времени со скоростью 4 км/час и ¼ времени со скоростью 8 км/час (опять бежал).
Пояснение: ½, ¼ и еще раз ¼ - это и есть «веса», сумма которых равна 1
Ответ: средняя скорость Vср= 8 км/час.
Почему Vср= 8 км/час (если забыть про формулу для среднего значения)? Рассмотрите произвольное время t. Какой путь прошел пешеход за время t? А теперь поделите путь на t – это и будет средняя скорость
Формула для среднего значения
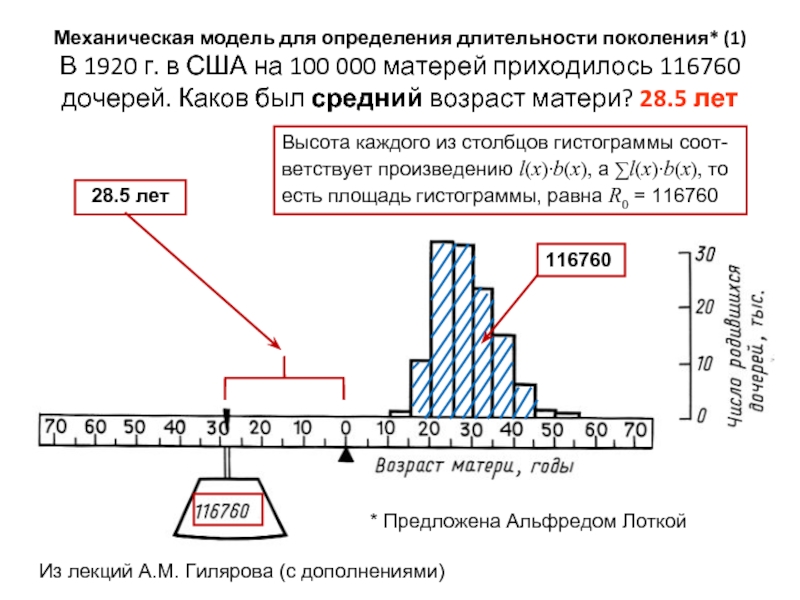
Слайд 13Механическая модель для определения длительности поколения* (1) В 1920 г. в США
Из лекций А.М. Гилярова (с дополнениями)
28.5 лет
Высота каждого из столбцов гистограммы соот-ветствует произведению l(x)∙b(x), а ∑l(x)∙b(x), то есть площадь гистограммы, равна R0 = 116760
* Предложена Альфредом Лоткой
116760
Слайд 14Тот факт, что балансир находится в равновесии, следует из формулы для
и из основных законов механики (о равенстве суммы моментов сил как усло-вии равновесия балансира)
Механическая аналогия (см. предыдущий слайд) состоит в том, что справа от оси балансира висит распределенный по возрастам груз общей «массой» 116760, а слева точечный груз (приходящийся на один возраст) с той же самой массой 116760. Спрашивается, на каком расстоянии от оси балансира нужно подвесить точечный груз, чтобы балансир находился в равновесии?
Механическая модель для определения длительности поколения (2)
или
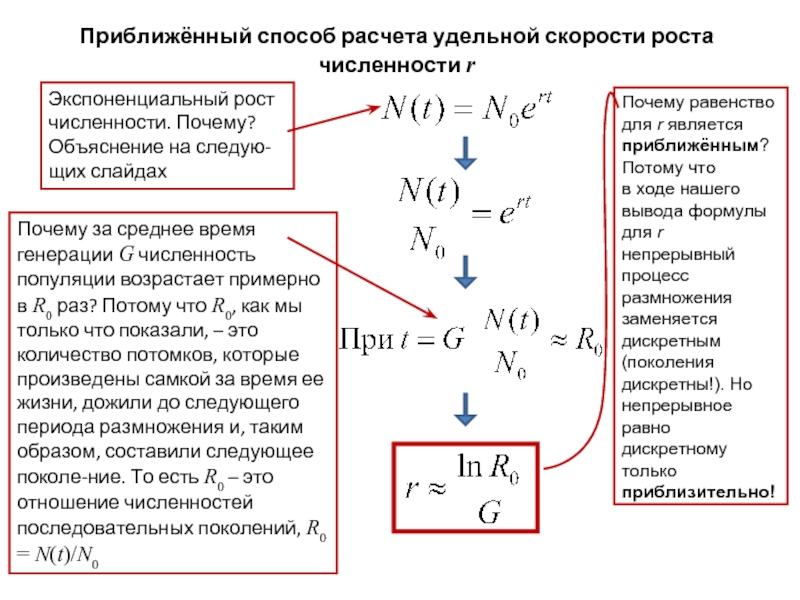
Слайд 15Приближённый способ расчета удельной скорости роста численности r
Экспоненциальный рост численности.
Почему за среднее время генерации G численность популяции возрастает примерно в R0 раз? Потому что R0, как мы только что показали, – это количество потомков, которые произведены самкой за время ее жизни, дожили до следующего периода размножения и, таким образом, составили следующее поколе-ние. То есть R0 – это отношение численностей последовательных поколений, R0 = N(t)/N0
Почему равенство для r является приближённым? Потому что
в ходе нашего вывода формулы для r непрерывный процесс размножения заменяется дискретным (поколения дискретны!). Но непрерывное равно дискретному только приблизительно!
Слайд 16
R0 - безразмерная величина,
которая показывает, во сколько раз возросла численность популяции
Из лекций А.М. Гилярова
Слайд 18Популяция, где по пять детей у молодых матерей (в год по
R0 = 2.5 G = 20 лет
Популяция, где по десять детей у более взрослых матерей (в год по ребенку с 31 до 40 лет):
R0 = 5 G = 35.5 лет
Кому давать орден «Мать-героиня»?
Из лекций А.М. Гилярова
Слайд 19r1 = (ln 2.5) / 20 =
0.916 / 20 =
r2 = (ln 5) / 35.5 =
1.609 / 35.5 = 0.0453 год-1
Кому давать орден «Мать-героиня»?
Из лекций А.М. Гилярова
Замечание 1. А почему все-таки правы те, кто присуждали орден за 10 детей? Потому что r1 может быть реализована только в чреде поколений, то есть если дочери этих матерей будут заводить столько же детей в столь же раннем возрасте (что, конечно, совсем необязательно)
Замечание 2. И величина r1, и величина r2, конечно, завышены, поскольку не учитывают, что la < 1. (Напомним, что R0 = b∙Ta∙la.)
Замечание 3 (точнее, вопрос). Почему r1 > r2 несмотря на то, что R0 у молодых матерей в 2 раза меньше? Ответ «потому что время генерации у них меньше» не годится, потому что время генерации у них меньше только в 1.5 раза.
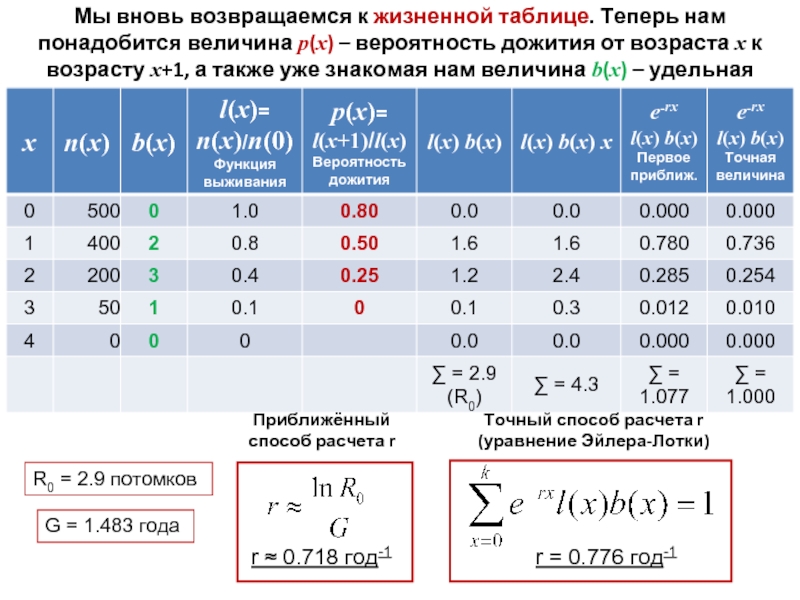
Слайд 20Мы вновь возвращаемся к жизненной таблице. Теперь нам понадобится величина p(x)
R0 = 2.9 потомков
G = 1.483 года
r ≈ 0.718 год-1
r = 0.776 год-1
Приближённый способ расчета r
Точный способ расчета r (уравнение Эйлера-Лотки)
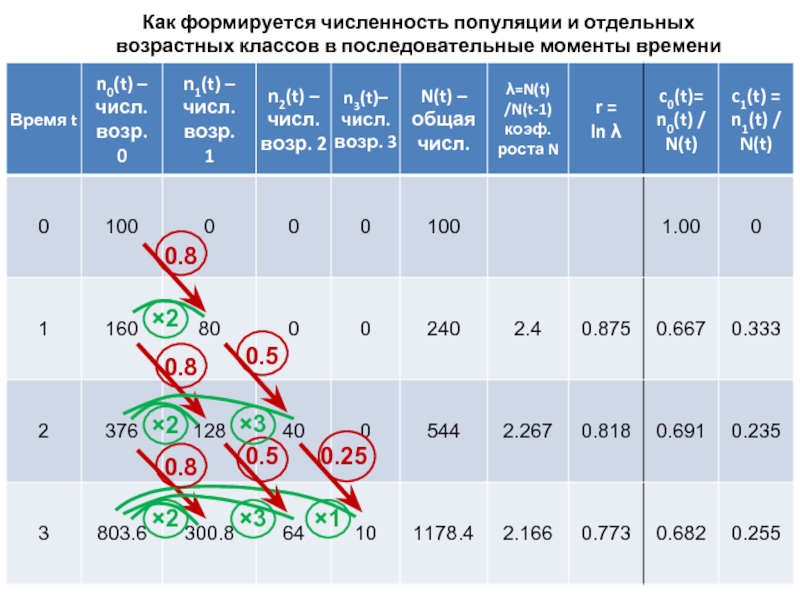
Слайд 21Параметры, которые вводятся на следующих слайдах
n0(t), n1(t), n2(t), n3(t) – численность
N(t) – общая численность популяции, N(t) = ∑ni(t), где i = 0, 1, 2, 3
λ = N(t)/N(t-1) – коэффициент роста численности N. Обратите внимание, что при экспоненциальном росте численности λ есть знаменатель геометрической прогрессии.
r – удельная скорость роста численности. Так как N(t) = N(t-1)∙er, то λ = er и r = ln λ
c0(t), c1(t), c2(t), c3(t) – доля особей возраста 0, 1, 2, 3 соответственно от общей численности популяции в момент времени t, то есть c0(t) = n0(t) / N(t), c1(t) = n1(t) / N(t) и т.д.
Слайд 22Как формируется численность популяции и отдельных возрастных классов в последовательные моменты
0.8
0.8
0.8
×2
×3
×2
×3
×2
×1
0.5
0.5
0.25
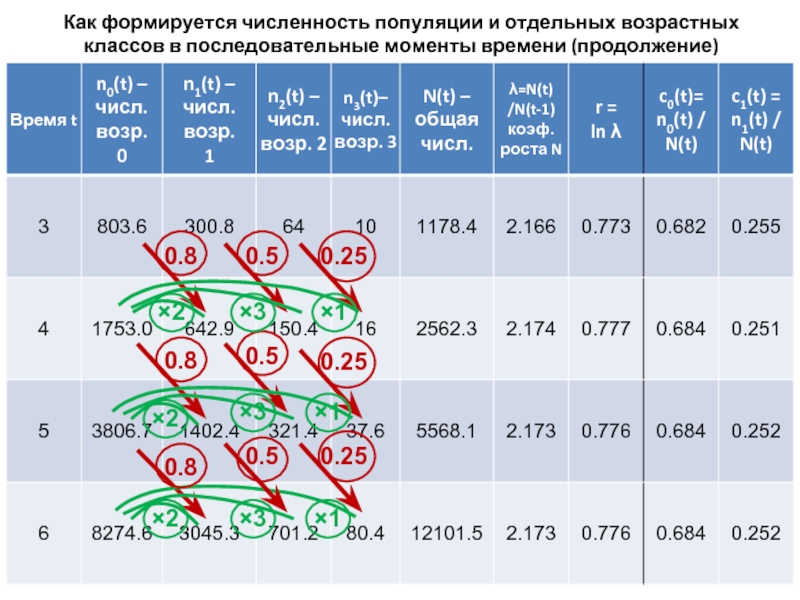
Слайд 23Как формируется численность популяции и отдельных возрастных классов в последовательные моменты
0.8
0.8
0.8
×2
×3
×2
×3
×2
×1
0.5
0.5
0.25
0.5
0.25
0.25
×3
×1
×1
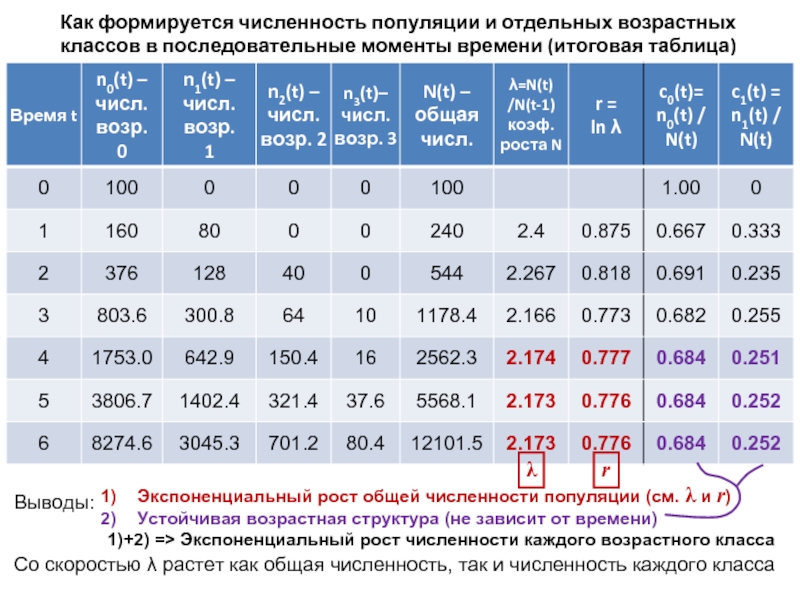
Слайд 24Экспоненциальный рост общей численности популяции (см. λ и r)
Устойчивая возрастная структура
1)+2) => Экспоненциальный рост численности каждого возрастного класса
Со скоростью λ растет как общая численность, так и численность каждого класса
Как формируется численность популяции и отдельных возрастных классов в последовательные моменты времени (итоговая таблица)
Выводы:
λ
r
Слайд 25Теорема Лотки
Alfred James Lotka (1880-1949)
Фото: http://www.eoearth.org
Lotka, A.J. (1907). Relation between birth
Sharpe, F.R. & Lotka, A.J. (1911). A problem in age distribution. Philosophical Magazine, 21: 435–438.
Если l(x) и b(x) кривые всех последовательно нарождающихся в популяции когорт в течение достаточно длительного времени одинаковы, то независимо от начальной возрастной структуры в популяции с течением времени установится устойчивая, неизменная во времени возрастная структура, и численность такой популяции будет расти в геометри-ческой прогрессии.
Слайд 27Матрицы Лесли (Paul H. Leslie, британский эколог):
самое общее, приблизительное представление о
Численность особей разных возрастных классов в последовательные моменты времени (т.е. то, чем мы только что занимались), на самом деле рассчитывают не с помощью жизненной таблицы, а с помощью матриц Лесли. То, что мы только что делали с помощью стрелок и цифр в кружочках, делают путем умножения матрицы Лесли на вектор возрастного состава по правилам умножения матриц. Записывается это так:
Вектор возрастного состава в момент t+1
Вектор возрастного состава в момент t
Матрица Лесли L
Матрица Лесли позволяет перейти от возрастного состава популяции в момент времени t к возрастному составу в момент времени t+1. Поэтому ее называют прогностической матрицей (population projection matrix). Лесли догадался, как нужно записать переходную матрицу L, чтобы переход от возрастного состава в момент t к возрастному составу в момент t+1 можно было осуществить, опираясь на обычные правила матричного умножения. Матрица Лесли основана на величинах b(x) и p(x) из жизненной таблицы. К сожалению, «устройство» матриц Лесли, как и правила умножения матриц (если Вы их не знаете), находятся за пределами нашего курса ☹ ☺
Матрица Лесли – это один из (немногих!) универсальных инст-рументов экологии,
о которых шла речь в первой лекции
Слайд 28Для тех, кто знаком с основными понятиями линейной алгебры, на этом
Связь между матрицей Лесли, уравнением Эйлера-Лотки и коэффициентом роста численности λ
(2) Уравнение Эйлера-Лотки
(1) Коэффициент роста численности λ
(5) Уравнение Эйлера-Лотки – это характеристический многочлен матрицы Лесли
(3) λ – это наибольшее собственное число матрицы Лесли
(4) Вектор устойчивого возрастного состава – это правый собственный вектор матрицы Лесли
Слайд 29Значение теоремы Лотки
Иногда полагают, что в геометрической прогрессии растут только «простые»,
Слайд 30Фундаментальное значение роста в геометрической прогрессии
“Geometrical ratio of increase
A struggle for
Задача: Проверьте Дарвина! ☺ У меня получилось 878 лет!
Charles Darwin (1809-1882)
Фото: http://en.wikipedia.org/wiki/Charles_Darwin
Слайд 31Вслед за Дарвином считаем слонов … ☺
Согласно Дарвину, слониха за время
e0.0183 x = 9500000, откуда 0.0183 x = ln(9500000) = 16.067.
x = 878 лет
А за 750 лет, о которых говорит Дарвин, численность слоних составит только e0.0183∙750 = 913,465 особей, или 1,826,929 самцов и самок, что в 10 раз меньше того, что получилось у Дарвина!
Фото:
http://en.wikipedia.org/wiki/File:African_Bush_Elephants.jpg
Слайд 32 – количество родившихся в момент времени t
Уравнение
(внизу в красной рамке его непрерывный аналог)
0
t-x
t
– количество родившихся в момент времени t
Факт экспоненциального роста общей численности, который используется в ходе этого доказательства, не доказан! Он следует из теоремы Лотки
Основные демографические понятия и соотношения: уравнение для r
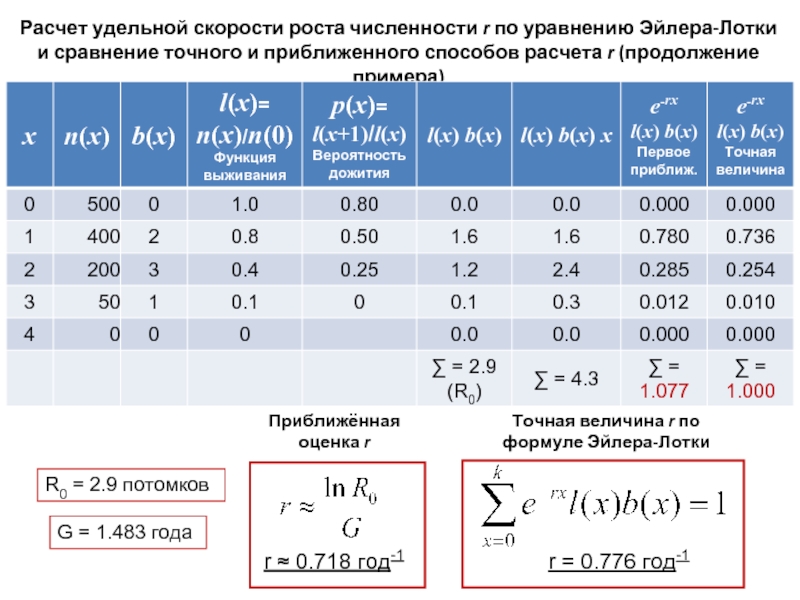
Слайд 33Расчет удельной скорости роста численности r по уравнению Эйлера-Лотки и сравнение
R0 = 2.9 потомков
G = 1.483 года
r ≈ 0.718 год-1
r = 0.776 год-1
Приближённая оценка r
Точная величина r по формуле Эйлера-Лотки
Слайд 34Как найти r из уравнения Эйлера-Лотки?
Выразить r из уравнения Эйлера-Лотки
В Excel решение уравнений осуществляет надстройка (Add-in), которая называется «Поиск решения» ([Equation] Solver). Для численного решения уравнения нужно задать начальное значение r, которое находят по приближенной формуле r = (lnR0)/G. Решение уравнения Эйлера-Лотки в условиях наше-го численного примера дано на следующих слайдах.
В пакете R решение уравнений осуществляется, например, с помощью функции uniroot
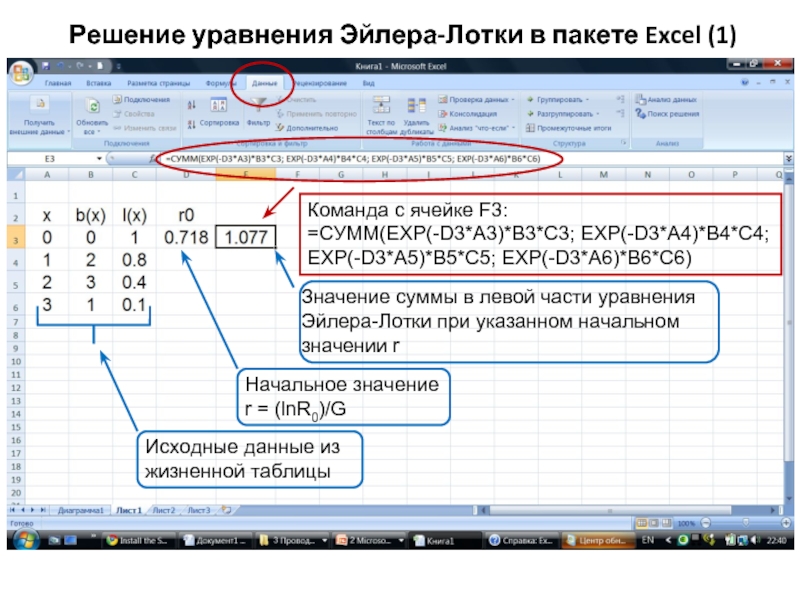
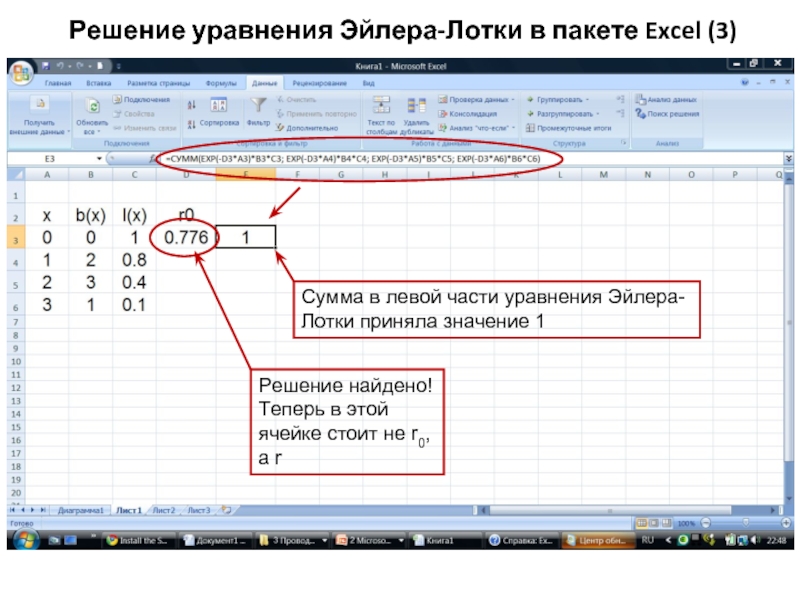
Слайд 35Решение уравнения Эйлера-Лотки в пакете Excel (1)
Исходные данные из жизненной
Начальное значение
r = (lnR0)/G
Значение суммы в левой части уравнения Эйлера-Лотки при указанном начальном значении r
Команда с ячейке F3:
=СУММ(EXP(-D3*A3)*B3*C3; EXP(-D3*A4)*B4*C4; EXP(-D3*A5)*B5*C5; EXP(-D3*A6)*B6*C6)
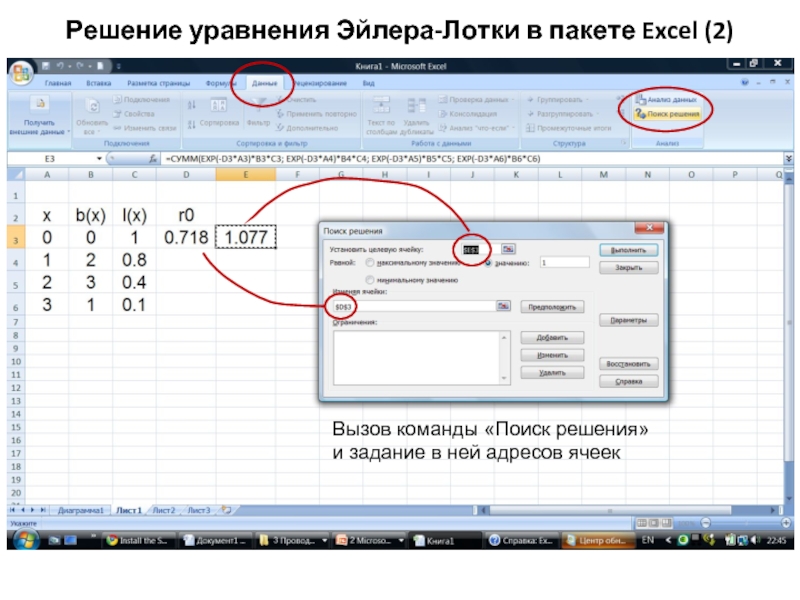
Слайд 36Решение уравнения Эйлера-Лотки в пакете Excel (2)
Вызов команды «Поиск решения»
Слайд 37Сумма в левой части уравнения Эйлера-Лотки приняла значение 1
Решение найдено! Теперь
Решение уравнения Эйлера-Лотки в пакете Excel (3)
Слайд 38Пример расчета r по формуле Эйлера-Лотки, или находится ли пятнистая неясыть
Фото:http://en.wikipedia.org/wiki/Strix_occidentalis
Пятнистая неясыть распространена
на западе Северной Америки
Карта: The IUCN Red List of Threatened Species http://www.iucnredlist.org/apps/redlist/details/143247/0
«Этот вид птиц был причиной значительных разногласий в конце 1980-х и начале 1990-х годов, так как в результате присвоения статуса «находящийся под угрозой вид» деревообрабатывающая промышленность не могла начать разработку млн. га старых лесов в штатах Вашингтон, Орегон и Калифорния.» (Википедия)
«The controversy pitted individual loggers and small sawmill owners against environmen-talists. Bumper stickers reading Kill a Spotted Owl—Save a Logger and I Like Spotted Owls—Fried appeared to support the loggers.» (Wikipedia)
Strix occidentalis
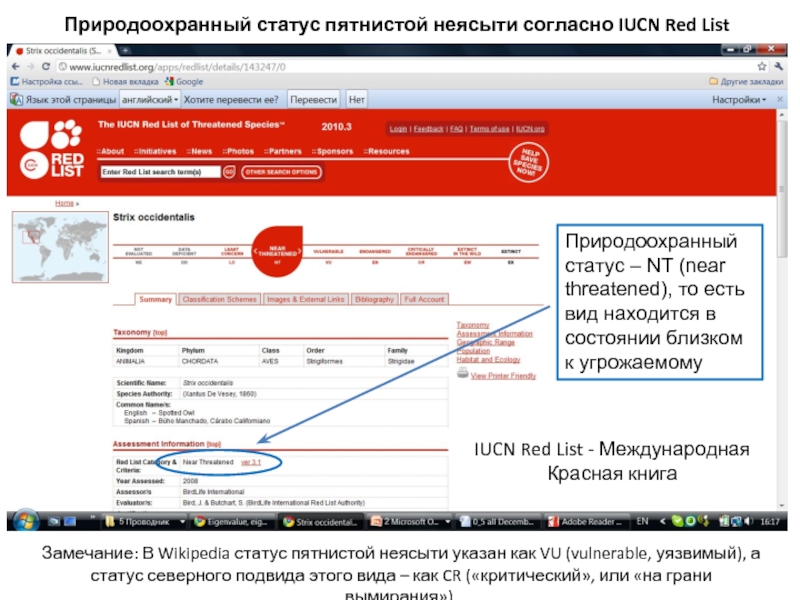
Слайд 39IUCN Red List - Международная Красная книга
Замечание: В Wikipedia статус пятнистой
Природоохранный статус – NT (near threatened), то есть вид находится в состоянии близком к угрожаемому
Природоохранный статус пятнистой неясыти согласно IUCN Red List
Слайд 40Расчет r (точнее, λ) по Russel Lande (Oecologia 1988 75: 601-607)
Начинаем
Преобразуем и упростим ту его форму, которая записана справа
(1)
Пусть a – возраст наступления половой зрелости, тогда в сумму (1) войдут только члены, начиная с возраста a, поскольку для более молодых возрастов b(x) = 0
Примем, что b(x) = b – это средняя удельная рождаемость по всем возрастам (тогда ее можно вынести за знак суммы в уравнении (1))
При x = a l(x) = la, где la – доля особей, доживших до половой зрелости (то есть до возраста a)
Примем, что вероятность дожития p(x) = l(x+1)/l(x) после достижения возраста a (то есть у взрослых особей) не зависит от возраста; p(x) = p
При x > a выразим l(x) через p: l(a+1) = la∙p, l(a+2) = la∙ p2, l(a+3) = la∙p3 и т.д. В общем виде
Слайд 41Преобразование уравнения Эйлера-Лотки (продолжение)
Мы провели замену переменной (x-a = z) и
Из этого уравнения можно найти λ!
Слайд 42Демографические характеристики пятнистой неясыти (по Lande 1988)
Самки первый раз размножаются
Самки приносят 0.48 потомков обоего пола в год (с учетом того, что самки не каждый год размножаются), то есть 2∙ b = 0.48 и b = 0.24 самок в год (принимая, что соотношение полов в помете составляет 1:1)
Доля особей, доживающих до половой зрелости (то есть до a = 3 года) равна la = 0.0722
Вероятность дожития у взрослых особей за год составляет p = 0.942
Подставляем эти величины в уравнение для λ
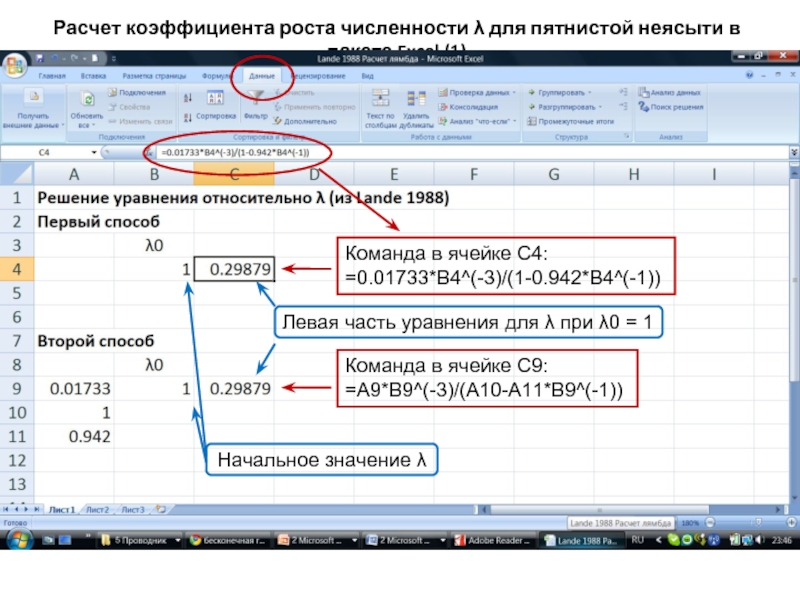
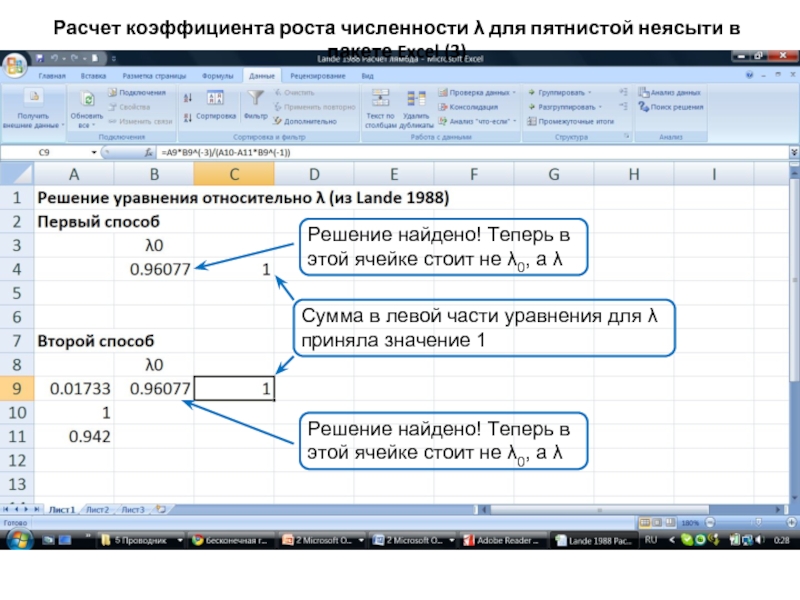
Слайд 43Расчет коэффициента роста численности λ для пятнистой неясыти в пакете Excel
Команда в ячейке C4:
=0.01733*B4^(-3)/(1-0.942*B4^(-1))
Начальное значение λ
Команда в ячейке С9:
=A9*B9^(-3)/(A10-A11*B9^(-1))
Левая часть уравнения для λ при λ0 = 1
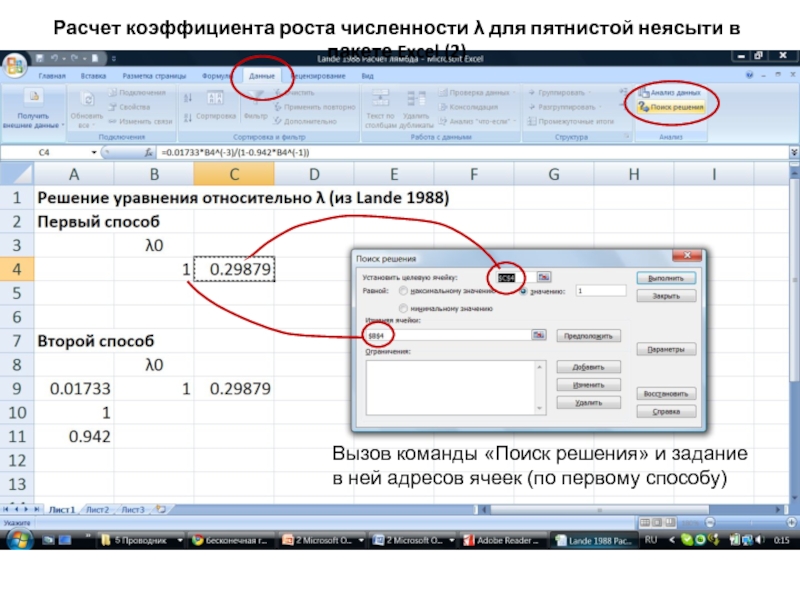
Слайд 44Вызов команды «Поиск решения» и задание в ней адресов ячеек (по
Расчет коэффициента роста численности λ для пятнистой неясыти в пакете Excel (2)
Слайд 45Сумма в левой части уравнения для λ приняла значение 1
Решение найдено!
Решение найдено! Теперь в этой ячейке стоит не λ0, а λ
Расчет коэффициента роста численности λ для пятнистой неясыти в пакете Excel (3)
Слайд 46Заключение
При указанных значениях демографических параметров пятнистая неясыть находится в стабильном состоянии
Слайд 47Согласно теореме Лотки (см. также рассмотренный выше пример формирования возрастных классов
Возрастной состав
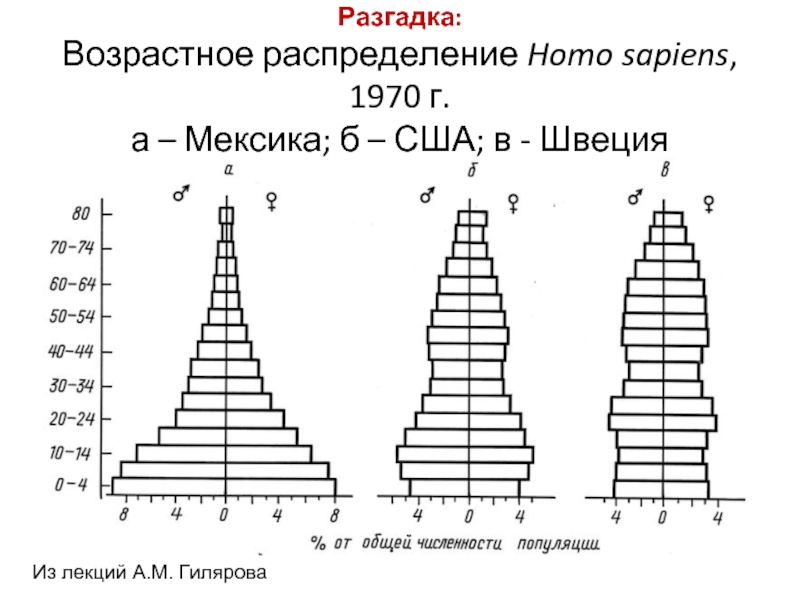
Слайд 48Возрастное распределение Homo sapiens, 1970 г. а – Мексика; б –
Рисунок из лекций А.М. Гилярова
Загадка:
Здесь показаны возрастные распределения населения трех стран – Швеции, Мексики и США. Какой стране принадлежит каждое из этих распределений?
Возраст, годы
Слайд 49Разгадка: Возрастное распределение Homo sapiens, 1970 г. а – Мексика; б –
Из лекций А.М. Гилярова
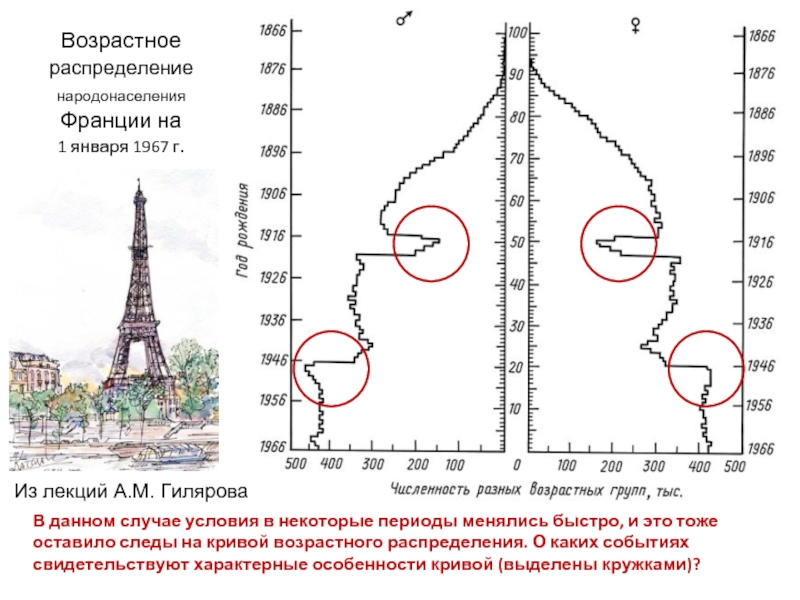
Слайд 50Возрастное распределение народонаселения Франции на
1 января 1967 г.
Из лекций А.М.
В данном случае условия в некоторые периоды менялись быстро, и это тоже оставило следы на кривой возрастного распределения. О каких событиях свидетельствуют характерные особенности кривой (выделены кружками)?
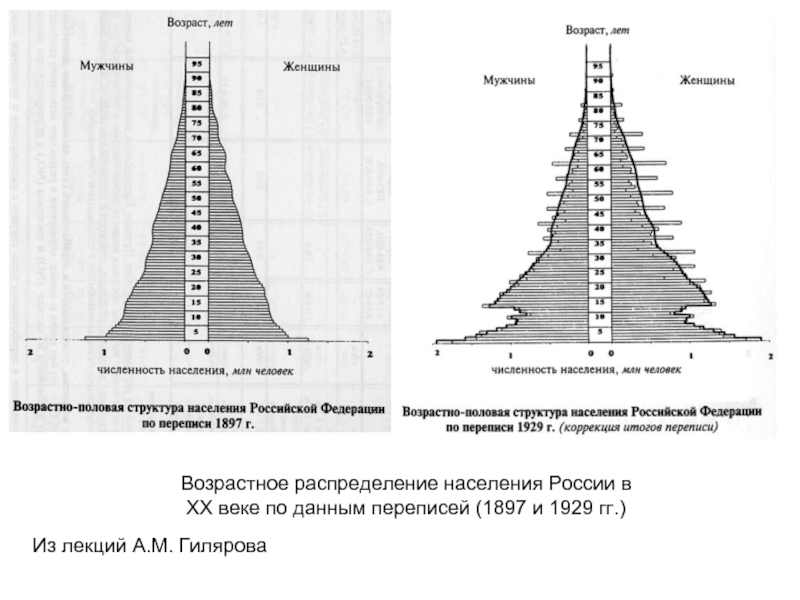
Слайд 51Возрастное распределение народонаселения
России
на
1 января 1997 г.
Из лекций А.М.
Бэби-бум 1987 г.?