- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы биореологии и гемодинамики. (Лекция 4) презентация
Содержание
- 1. Основы биореологии и гемодинамики. (Лекция 4)
- 2. Биореология – это наука, которая изучает упругие
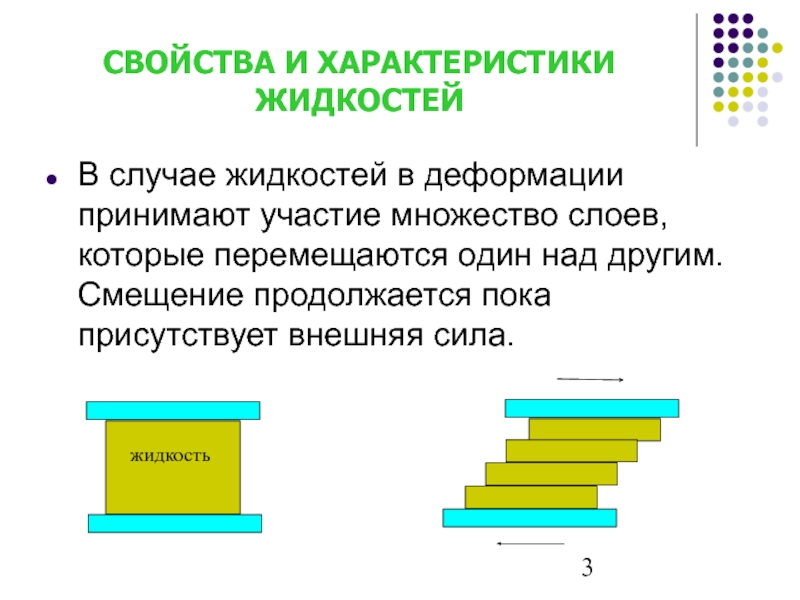
- 3. В случае жидкостей в деформации принимают участие
- 4. Вязкость Жидкости проявляют сопротивление движению из-за своей
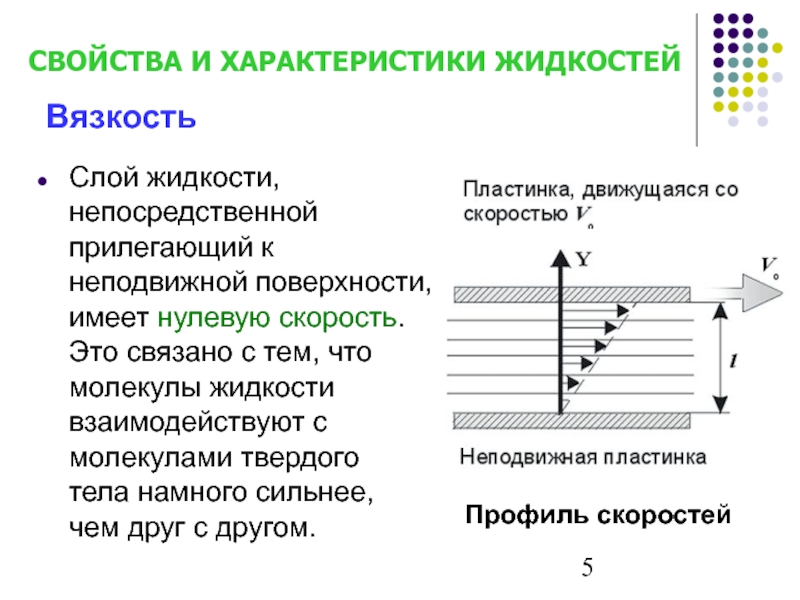
- 5. Слой жидкости, непосредственной прилегающий к неподвижной поверхности,
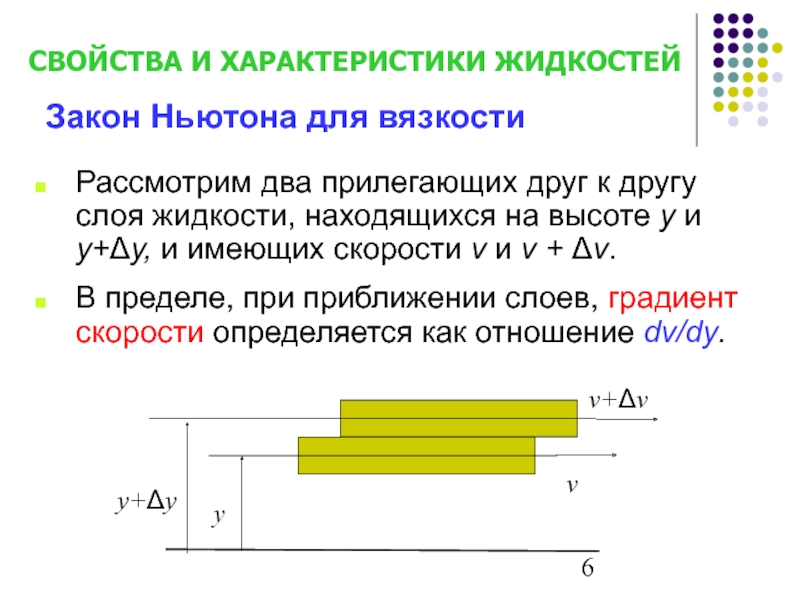
- 6. Рассмотрим два прилегающих друг к другу слоя
- 7. Ньютон предположил, что сдвигающая сила (между слоями)
- 8. Величина η называется еще динамической вязкостью (или
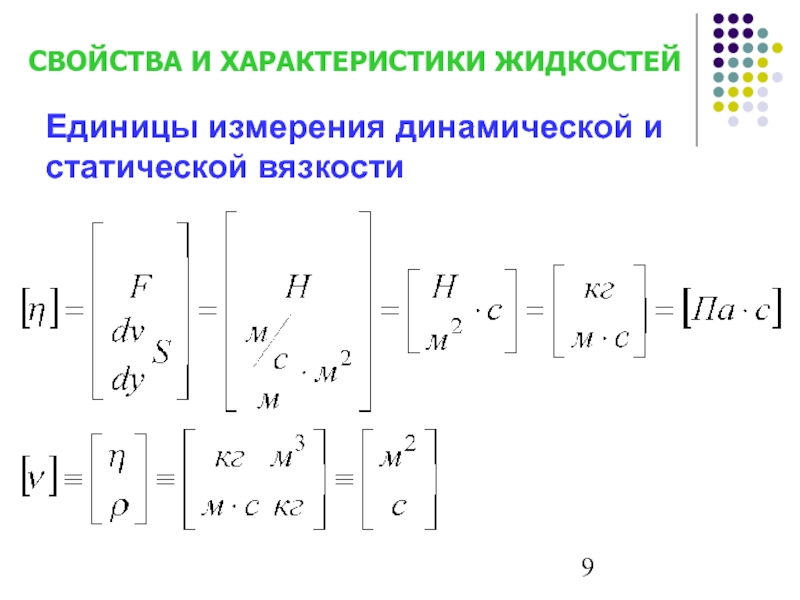
- 9. Единицы измерения динамической и статической вязкости СВОЙСТВА И ХАРАКТЕРИСТИКИ ЖИДКОСТЕЙ
- 10. НЬЮТОНОВСКИЕ И НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ Жидкость называется ньютоновской,
- 11. Кровь является неньютоновской жидкостью. Вязкость человеческой
- 12. Кровь состоит из большого числа макромолекул (альбумина
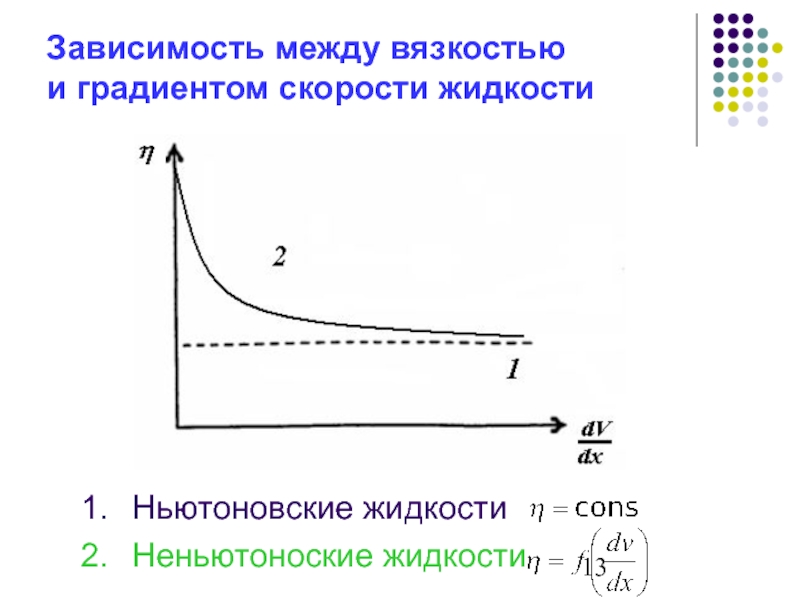
- 13. Ньютоновские жидкости Неньютоноские жидкости Зависимость между вязкостью и градиентом скорости жидкости
- 14. Модель Кессона Реологические свойства крови могут
- 15. Жидкости в движении Течение называется однородным, если
- 16. Линии тока Линиями тока называются
- 17. Два типа течения Первый тип потока
- 18. Число Рейнольдса Re < Re кр ‒
- 19. Для трубы с круглым сечением при нормальных
- 20. Распределение скоростей в вязкой жидкости, текущей через трубу Жидкости в движении
- 21. где: l – длина трубы R
- 22. Основы гидродинамики. Идеальная жидкость. “Идеальная жидкость” является
- 23. где S1 и S2 – площади
- 24. p - давление, ρ - плотность, v
- 25. Уравнение Бернулли является следствием из закона сохранения энергии Жидкости в движении
- 26. Элементы гемодинамики Кровеносная система представляет из себя
- 27. Механизмы циркуляции крови Сердце ‒ это
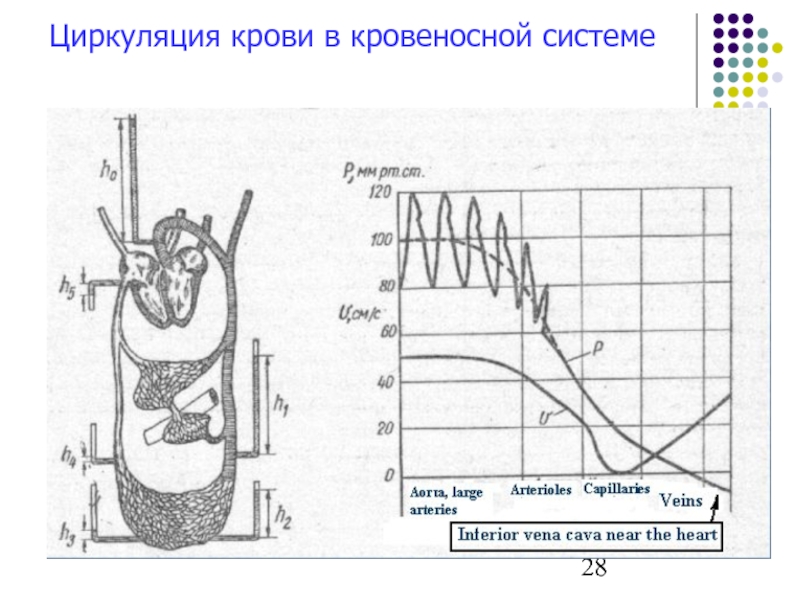
- 28. Циркуляция крови в кровеносной системе
- 29. Модели кровеносной системы Уравнение Пуазейля
- 30. Пульсовая волна Кровь циркулирует по венам и
- 31. Модель Франка Все крупные кровеносные сосуды представляются
- 32. Пульсовая волна Скорость распространения пульсовой волны в
- 33. Эквивалентная электрическая модель течения крови по сосудам
- 34. Современная электрическая модель циркуляции крови – четырехэлементная обобщенная параметрическая артериальная модель
- 35. Выводы: 1. Рассмотрены основные упругие свойства жидкостей
- 36. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Лекция 4
Основы биореологии и гемодинамики
Лектор: к.т.н. Якимов А.Н.
Кафедра медицинской и биологической
ГУ «Луганский государственный медицинский университет»
Слайд 2Биореология – это наука, которая изучает упругие свойства твердых тел, жидкостей
Гемодинамика описывает движение этих сред под действие внешних и внутренних сил.
БИОРЕОЛОГИЯ И ГЕМОДИНАМИКА
Слайд 3В случае жидкостей в деформации принимают участие множество слоев, которые перемещаются
СВОЙСТВА И ХАРАКТЕРИСТИКИ ЖИДКОСТЕЙ
Слайд 4Вязкость
Жидкости проявляют сопротивление движению из-за своей вязкости, или, как ее еще
Чем выше вязкость жидкости, тем больше возникающее между ее слоями сопротивление движению.
Явление внутреннего трения возникает из-за взаимодействия молекул, находящихся в соседних слоях жидкости.
СВОЙСТВА И ХАРАКТЕРИСТИКИ ЖИДКОСТЕЙ
Слайд 5Слой жидкости, непосредственной прилегающий к неподвижной поверхности, имеет нулевую скорость. Это
Профиль скоростей
Вязкость
СВОЙСТВА И ХАРАКТЕРИСТИКИ ЖИДКОСТЕЙ
Слайд 6Рассмотрим два прилегающих друг к другу слоя жидкости, находящихся на высоте
В пределе, при приближении слоев, градиент скорости определяется как отношение dv/dy.
Закон Ньютона для вязкости
СВОЙСТВА И ХАРАКТЕРИСТИКИ ЖИДКОСТЕЙ
Слайд 7Ньютон предположил, что сдвигающая сила (между слоями) пропорциональна градиенту скорости, перпендикулярному
Величина η называется коэффициентом вязкости жидкости. Коэффициент вязкости зависит от физических свойств и строения жидкости (т.е. степени взаимодействия молекул).
Закон Ньютона для вязкости
СВОЙСТВА И ХАРАКТЕРИСТИКИ ЖИДКОСТЕЙ
Слайд 8Величина η называется еще динамической вязкостью (или просто вязкостью) жидкости.
Коэффициент η
Большинство жидкостей подчиняются уравнению Ньютона (так называемые «ньютоновские жидкости»).
Для жидкостей η уменьшается с увеличением температуры.
Другим свойством жидкости является ее кинематическая вязкость ν = η /ρ .
Закон Ньютона для вязкости
СВОЙСТВА И ХАРАКТЕРИСТИКИ ЖИДКОСТЕЙ
Слайд 10НЬЮТОНОВСКИЕ И НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ
Жидкость называется ньютоновской, если ее течение подчиняется уравнению
Жидкости, которые не удовлетворяют уравнению Ньютона называются неньютоновскими. Их вязкость зависит, в частности, от градиента скорости (высокомолекулярные органические смеси, эмульсии, суспензии и т.д.).
Слайд 11
Кровь является неньютоновской жидкостью. Вязкость человеческой крови находится в пределах от
СОСТАВ И СВОЙСТВА КРОВИ
Слайд 12Кровь состоит из большого числа макромолекул (альбумина (белок), липидов, карбогидратов) и
СОСТАВ И СВОЙСТВА КРОВИ
Эритроциты оказывают наибольшее влияние на реологию крови. Они занимают около 46 % всего объема крови. Это значение (0.46) называется гематокритом крови.
Слайд 13Ньютоновские жидкости
Неньютоноские жидкости
Зависимость между вязкостью
и градиентом скорости жидкости
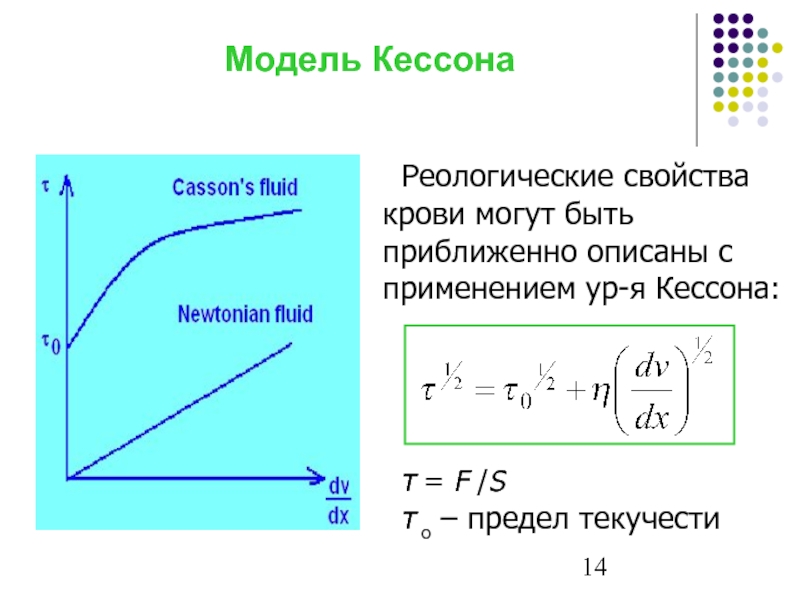
Слайд 14Модель Кессона
Реологические свойства крови могут быть приближенно описаны с применением
τ = F /S
τ o – предел текучести
Слайд 15Жидкости в движении
Течение называется однородным, если его свойства одинаковы во всем
Если величины va = vb = vc, pa = pb = pc и т.д. имеют одинаковые значение во всех точках, то такой поток ‒ однородный.
Однородный поток
Слайд 16Линии тока
Линиями тока называются линии, к которым векторы скорости
Однородный поток
Густота линий тока пропорциональна скорости.
Линии тока в случае однородного потока изображаются прямыми и параллельными друг другу линиями.
Жидкости в движении
Слайд 17
Два типа течения
Первый тип потока характерен для течения жидкости с низкой
Второй тип течения наблюдается при высоких скоростях перемещения жидкости и называется турбулентным. В нем частицы движутся не прямолинейно, но более беспорядочно, а слои жидкости смешиваются друг с другом.
Между полностью ламинарным и полностью турбулентным типом потока можно выделить переходную область.
Жидкости в движении
Слайд 18Число Рейнольдса
Re < Re кр ‒ ламинарное течение
Re > Re кр
Re ≈ Re кр ‒ переходное течение
Тип потока может быть определен с применением простого параметра - числа Рейнольдса:
Жидкости в движении
Слайд 19Для трубы с круглым сечением при нормальных условиях критическое значение числа
Re кр = 2000..4000
Таким образом:
Re < 2000: ламинарное течение
2000 < Re < 4000: переходное течение
Re > 4000: турбулентное течение
Число Рейнольдса
Жидкости в движении
Слайд 21где:
l – длина трубы
R – радиус трубы
(P1 – P2) –
Объем Q ньютоновской жидкости, протекающей за секунду через трубу с круглым поперечным сечением, равен:
Жидкости в движении
Закон Пуазейля
Слайд 22Основы гидродинамики.
Идеальная жидкость.
“Идеальная жидкость” является своеобразной идеализацией в гидродинамике.
Под идеальной
Жидкости в движении
Слайд 23
где S1 и S2 – площади поперечного сечения,
v1
Уравнение непрерывности потока
Жидкости в движении
Для идеальных жидкостей
Слайд 24p - давление, ρ - плотность, v – скорость,
g –
В уравнении Бернулли слагаемое p называется статическим давлением, ρgh ‒ гидростатическим давлением, а 1/2 ρv2 ‒ гидродинамическим давлением. Согласно этому уравнению полное давление гидродинамической системы остается постоянным.
Уравнение Бернулли
Жидкости в движении
Слайд 26Элементы гемодинамики
Кровеносная система представляет из себя закрытую систему эластичных сосудов: гидравлическую
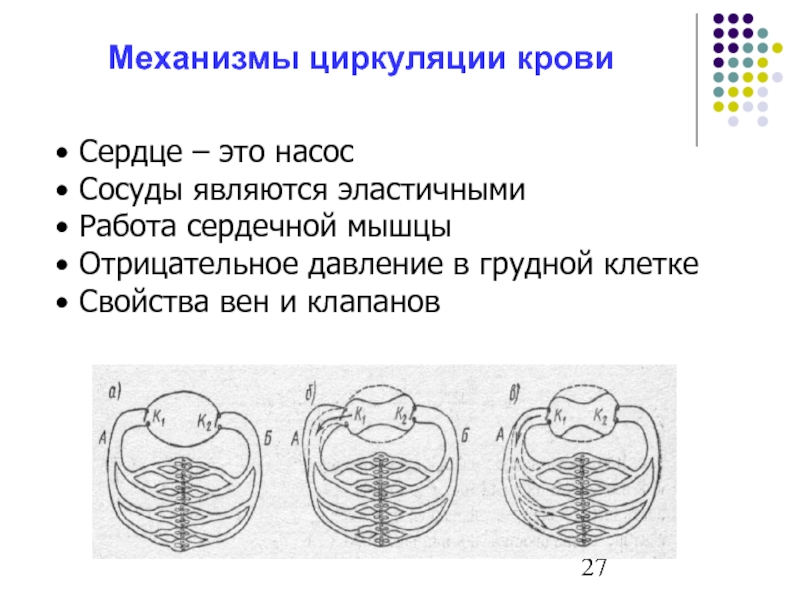
Слайд 27Механизмы циркуляции крови
Сердце ‒ это насос
Сосуды являются эластичными
Работа
Отрицательное давление в грудной клетке
Свойства вен и клапанов
Слайд 29Модели кровеносной системы
Уравнение Пуазейля
может быть записано в форме
где
Эта формула аналогично закону Ома
Разность давлений P1 – P2 является аналогией разность электрических потенциалов (напряжению). Т.о. по аналогии мы можем записать формулы для параллельно и последовательно соединенных проводников:
Слайд 30Пульсовая волна
Кровь циркулирует по венам и артериям, благодаря эластичности которых прерывный
Артерии представляют собой систему соединенных трубок с некоторой допустимой емкостью. Емкость эластичных кровеносных сосудов определяется степенью их растяжимости Di
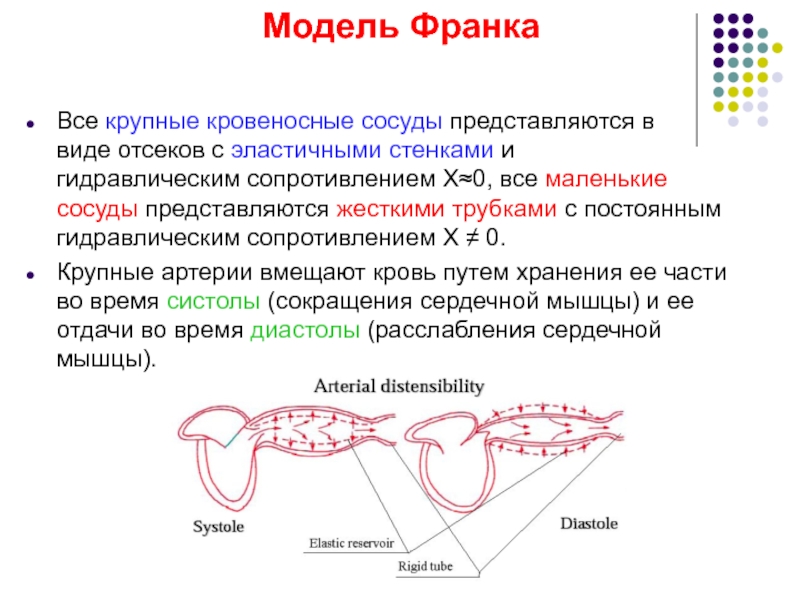
Слайд 31Модель Франка
Все крупные кровеносные сосуды представляются в
виде отсеков с эластичными стенками
Крупные артерии вмещают кровь путем хранения ее части во время систолы (сокращения сердечной мышцы) и ее отдачи во время диастолы (расслабления сердечной мышцы).
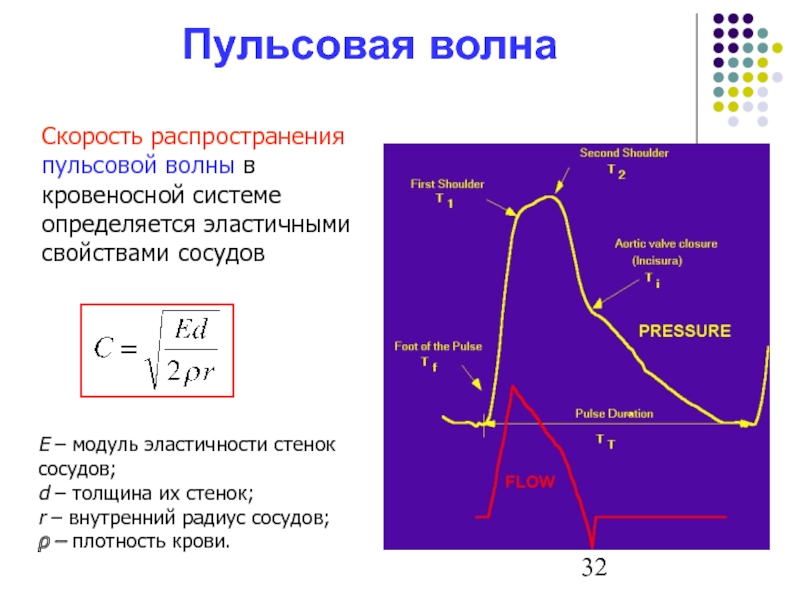
Слайд 32Пульсовая волна
Скорость распространения пульсовой волны в кровеносной системе определяется эластичными свойствами
E – модуль эластичности стенок сосудов;
d – толщина их стенок;
r – внутренний радиус сосудов;
ρ ‒ плотность крови.
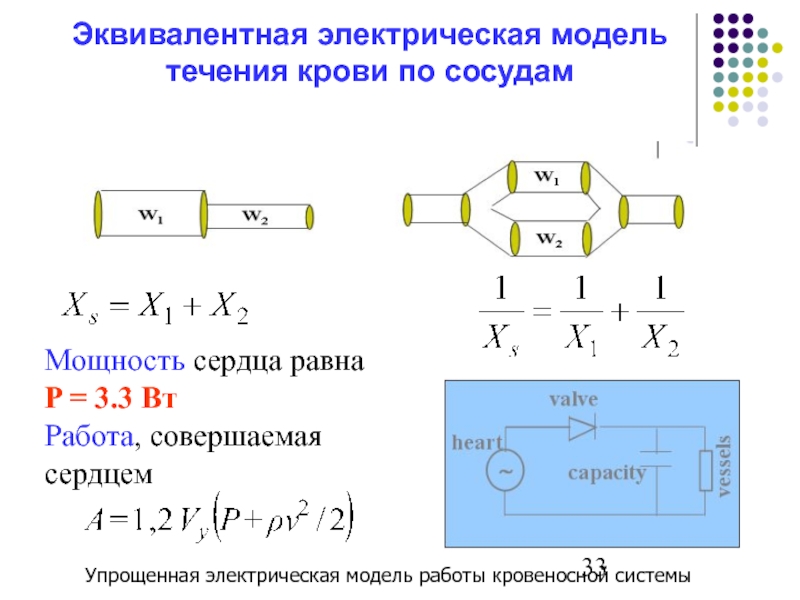
Слайд 33Эквивалентная электрическая модель течения крови по сосудам
Мощность сердца равна
P = 3.3
Работа, совершаемая сердцем
Упрощенная электрическая модель работы кровеносной системы
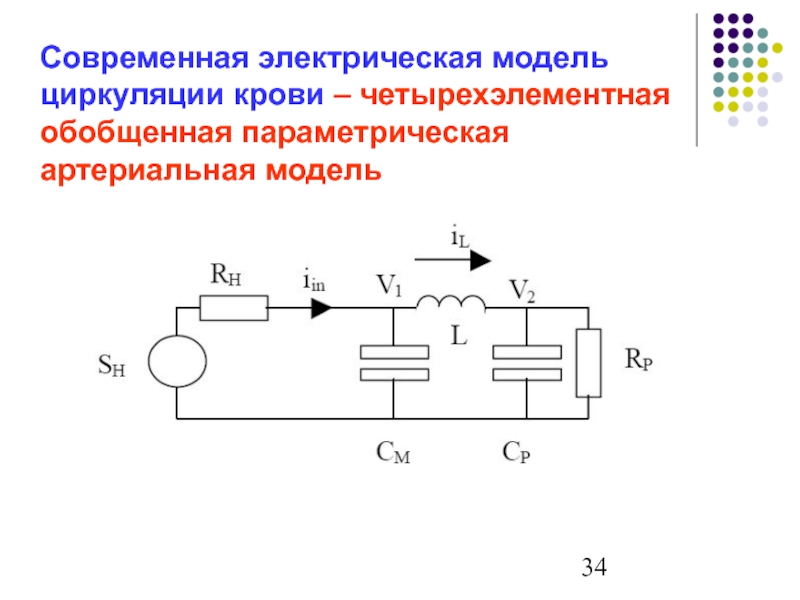
Слайд 34Современная электрическая модель циркуляции крови – четырехэлементная обобщенная параметрическая артериальная модель
Слайд 35Выводы:
1. Рассмотрены основные упругие свойства жидкостей
(статическая, динамическая вязкость и
2. Дано уравнение Ньютона для величины внутреннего трения в ньютоновских жидкостях и уравнение Кессона для оценки внутреннего трения крови (неньютоновской жидкости).
3. Рассмотрены основные типы течения жидкости и формула для вычисления характеризующего их числа Рейнольдса.
4. Приведены основные законы и уравнения движения идеальной несжимаемой жидкости:
уравнение непрерывности потока;
уравнение Пуазейля для удельного объема жидкости, протекающей по трубке;
уравнение Бернулли, учитывающее высоту, скорость и давление жидкости в различных участках потока.
5. Рассмотрено устройство и модели работы кровеносной системы человека (модель Франка и пульсовой волны).