- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
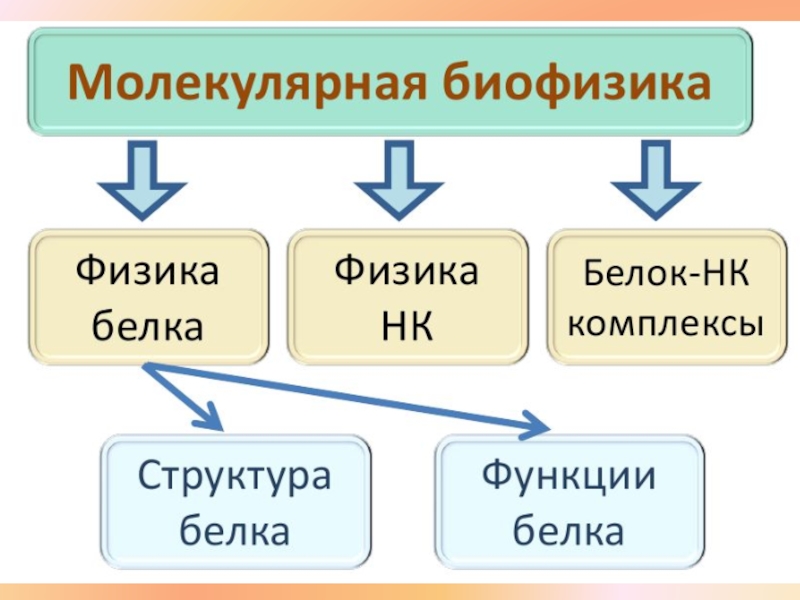
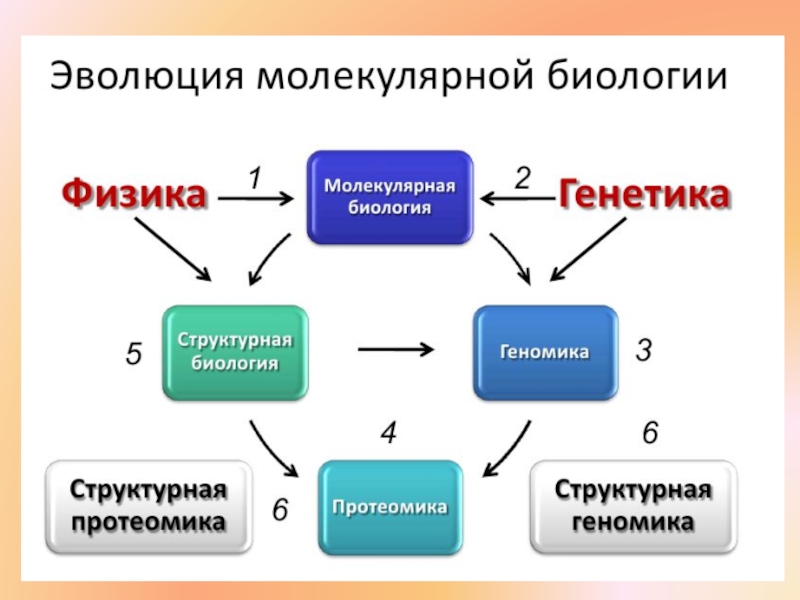
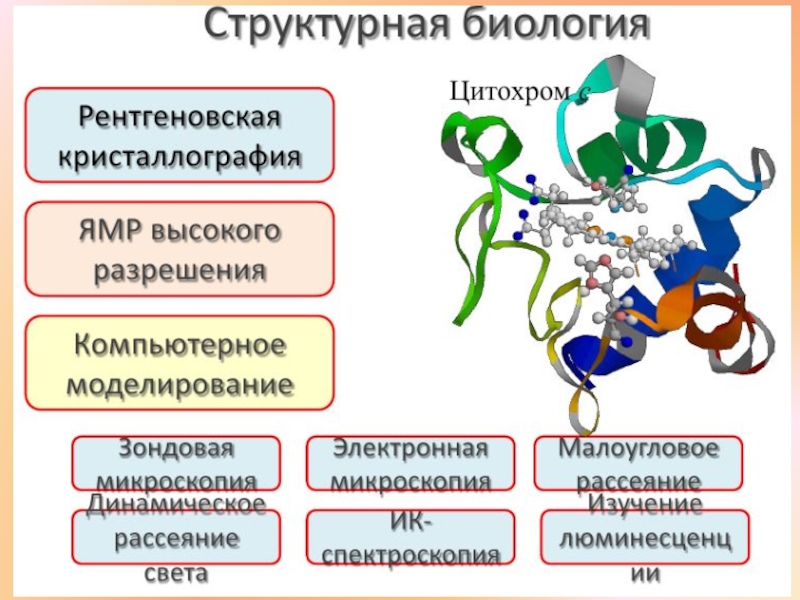
Молекулярная биофизика. Биологические макромолекулы в растворе, теория Дебая - Хюккеля презентация
Содержание
- 1. Молекулярная биофизика. Биологические макромолекулы в растворе, теория Дебая - Хюккеля
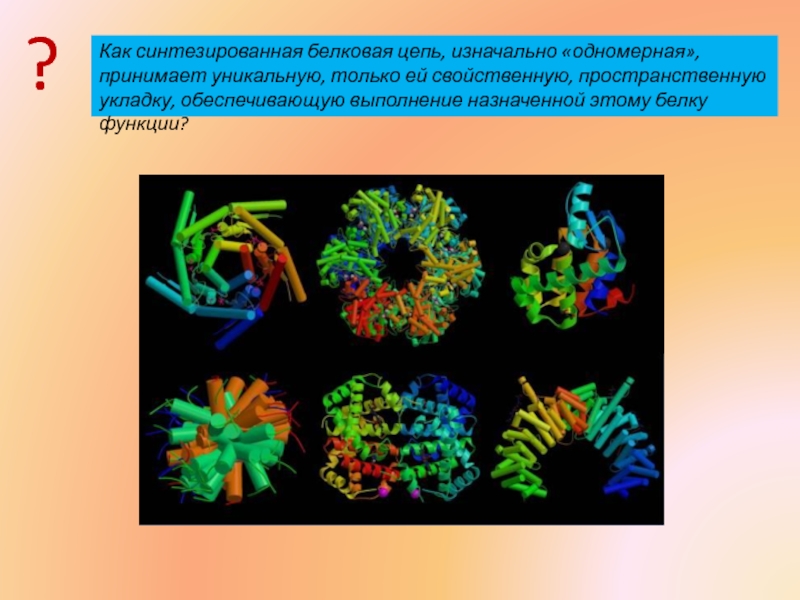
- 2. Как синтезированная белковая цепь, изначально «одномерная», принимает
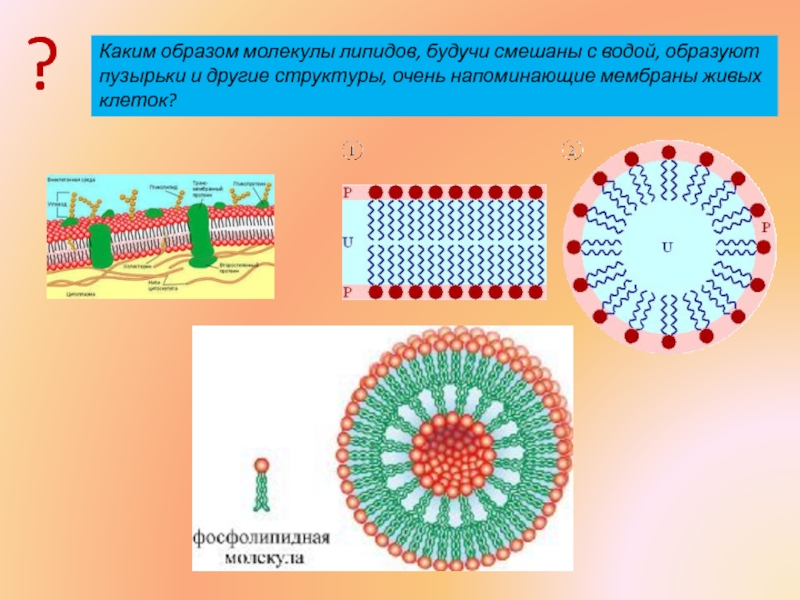
- 3. Каким образом молекулы липидов, будучи смешаны с
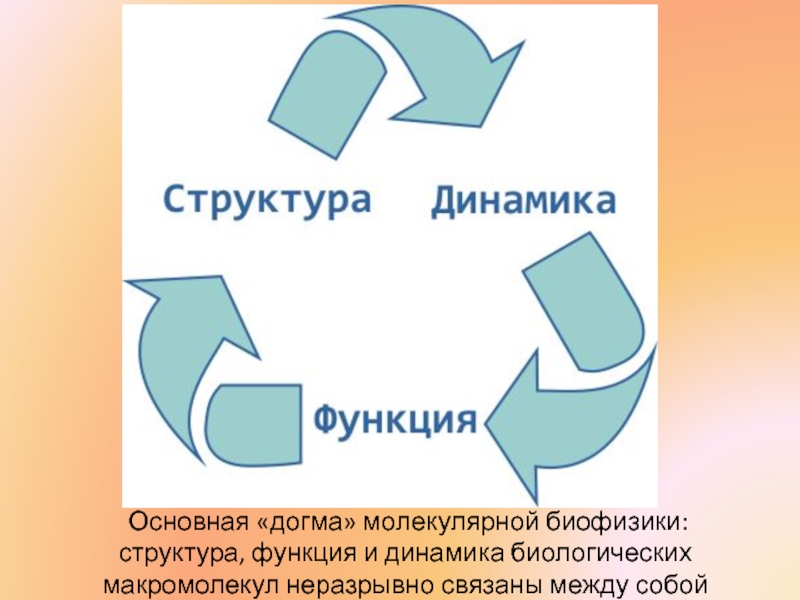
- 4. Основная «догма» молекулярной биофизики: структура,
- 5. Одним из первых биофизических экспериментов может считаться знаменитый
- 6. Одним из первых молекулярных биофизиков может считаться
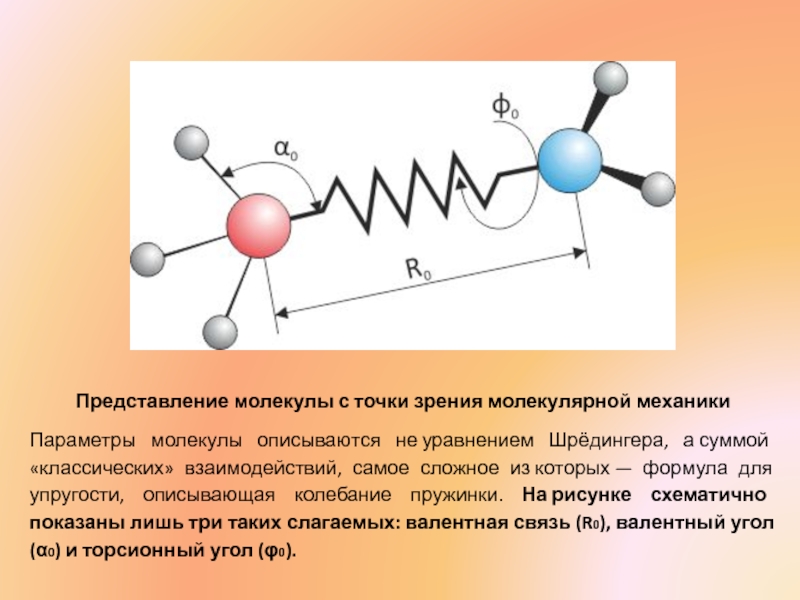
- 7. Представление молекулы с точки зрения молекулярной механики
- 17. Масс-спектроскопия (масс-спектроскопия,
- 22. СПЕЦИФИКА БИОМАКРОМОЛЕКУЛ СТАТИСТИЧЕСКИЙ ХАРАКТЕР ПОВЕДЕНИЯ, Т.К. БИОМАКРОМОЛЕКУЛЫ
- 23. Теория Дебая-Хюккеля Теория сильных электролитов (1923 г.)
- 24. БММ (белки, НК) содержат большое число ионизированных
- 25. Используем для решения уравнение Пуассона, которое связывает
- 26. Подставив в уравнение Пуассона (1) уравнения (2)
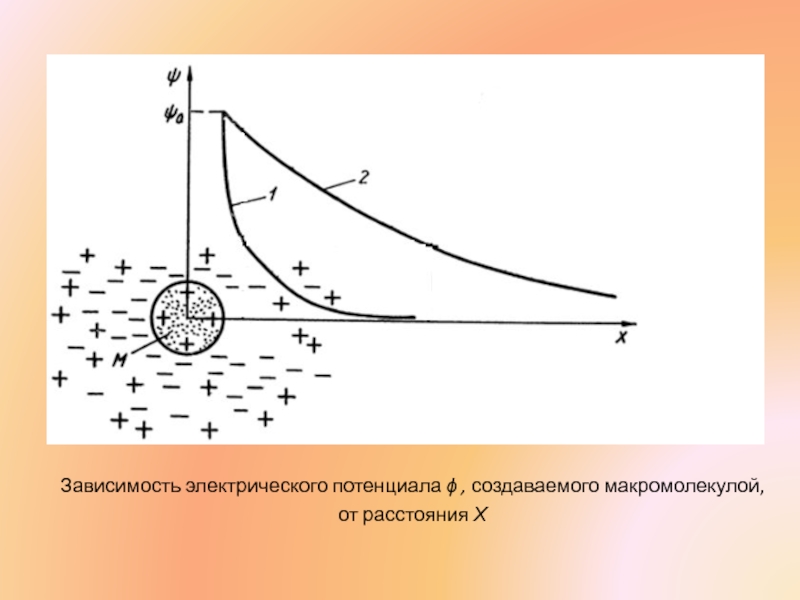
- 27. Зависимость электрического потенциала ϕ , создаваемого макромолекулой, от расстояния Х
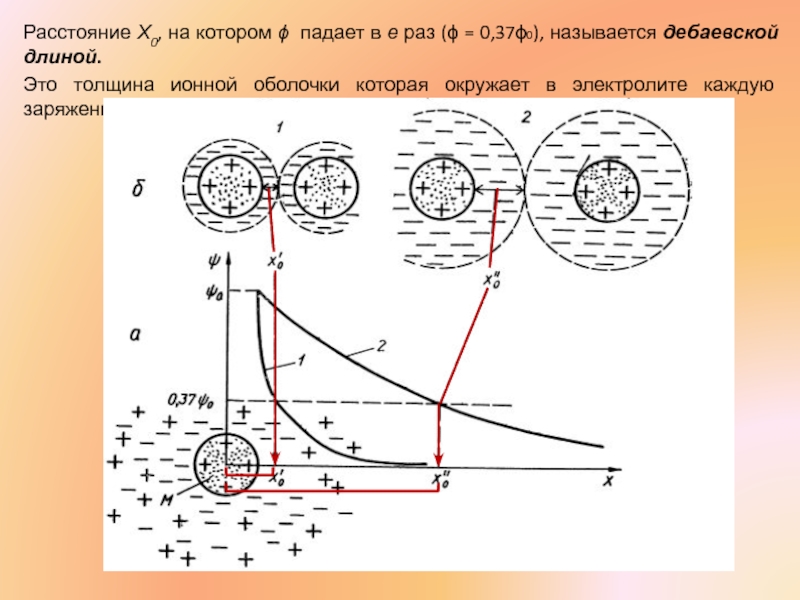
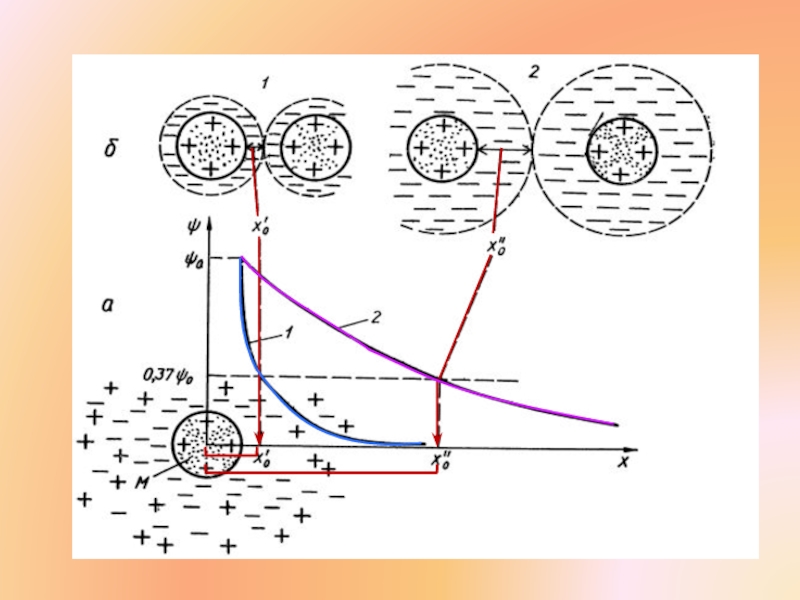
- 28. Расстояние Х0, на котором ϕ падает в
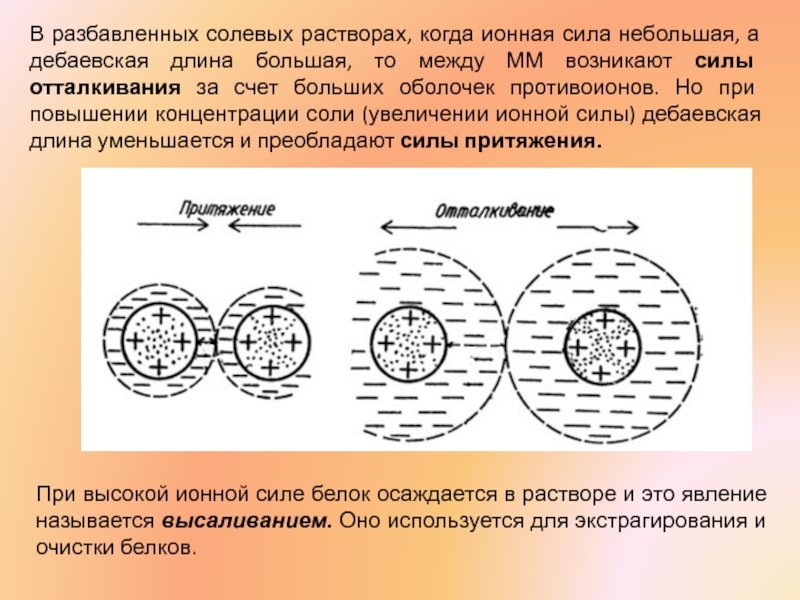
- 29. Влияние концентрации ионов на взаимодействие заряженных ММ
- 31. В разбавленных солевых растворах, когда ионная сила
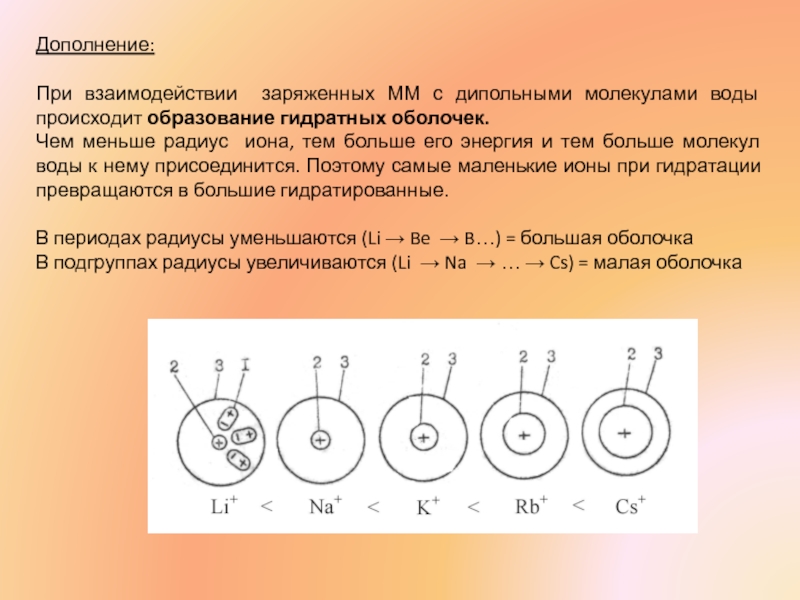
- 32. Дополнение: При взаимодействии заряженных ММ с
- 33. Лекция №2 «Конформация макромолекул. Виды
Слайд 2Как синтезированная белковая цепь, изначально «одномерная», принимает уникальную, только ей свойственную, пространственную
?
Слайд 3Каким образом молекулы липидов, будучи смешаны с водой, образуют пузырьки и
?
Слайд 4 Основная «догма» молекулярной биофизики: структура, функция и динамика биологических макромолекул
Слайд 5Одним из первых биофизических экспериментов может считаться знаменитый опыт Гальвани — во времена, когда
Luigi Galvani
1737—1798
Слайд 6Одним из первых молекулярных биофизиков может считаться
Эрвин Шрёдингер, чья книга «Что
(12.08.1887 - 4.01.1961)
Слайд 7Представление молекулы с точки зрения молекулярной механики
Параметры молекулы описываются не уравнением Шрёдингера,
Слайд 17Масс-спектроскопия
(масс-спектроскопия, масс-спектрография, масс-спектральный анализ, масс-спектрометрический анализ) — метод исследования вещества,
Слайд 22СПЕЦИФИКА БИОМАКРОМОЛЕКУЛ
СТАТИСТИЧЕСКИЙ ХАРАКТЕР ПОВЕДЕНИЯ, Т.К. БИОМАКРОМОЛЕКУЛЫ СОСТОЯТ ИЗ БОЛЬШОГО ЧИСЛА ОДНОТИПНЫХ
НАЛИЧИЕ НЕ ТОЛЬКО ХИМИЧЕСКИХ СВЯЗЕЙ, НО И ДРУГИХ ВЗАИМОДЕЙСТВИЙ РАЗНОГО ТИПА, ЧТО ОГРАНИЧИВАЕТ ЧИСЛО ВОЗМОЖНЫХ КОНФОРМАЦИЙ.
Слайд 23Теория Дебая-Хюккеля
Теория сильных электролитов (1923 г.)
Основные положения:
Сильные электролиты в водных растворах
При высокой концентрации ионов и малыми расстояниями между ними ионы взаимодействуют между собой (кулоновские взаимодействия);
Межионное взаимодействие приводит к тому, что каждый из ионов становится кружен «роем» противоионов, так называемой ионной атмосферой;
Межионное взаимодействие приводит к снижению подвижности ионов и уменьшает степень их участия в процессах, происходящих в растворах.
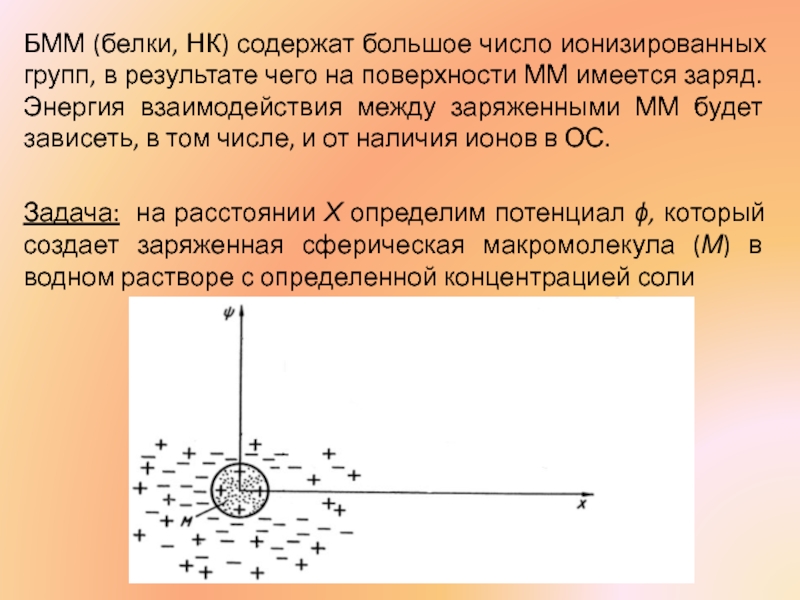
Слайд 24БММ (белки, НК) содержат большое число ионизированных групп, в результате чего
Задача: на расстоянии Х определим потенциал ϕ, который создает заряженная сферическая макромолекула (М) в водном растворе с определенной концентрацией соли
Слайд 25Используем для решения уравнение Пуассона, которое связывает плотность заряда (ρ) в
Также необходимо учесть, что на ориентацию ионов вблизи ММ будут влиять тепловые колебания, в результате чего количество ионов будет подчиняться распределению Больцмана:
(2)
(1)
Обозначим заряд иона i – типа ei и количество ионов в единице объема n’i
Электрическая энергия иона
Тепловая
энергия иона
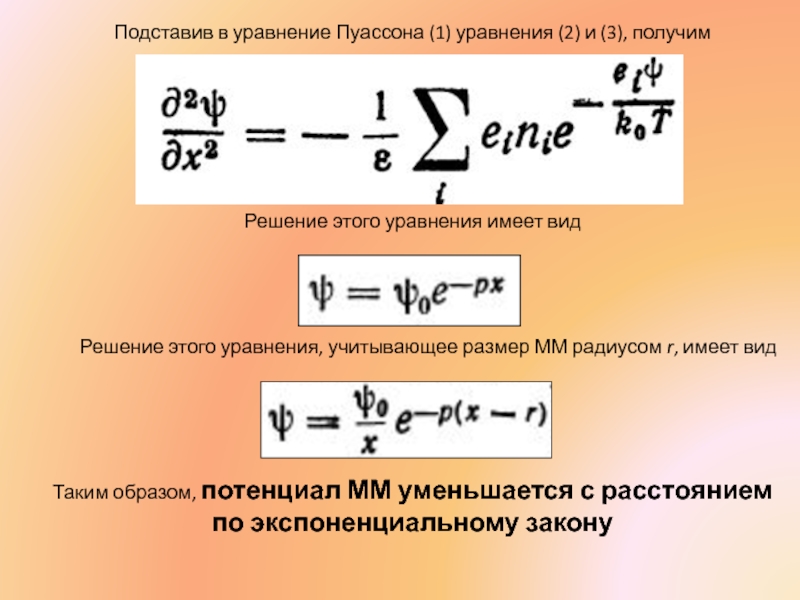
Подставив в уравнение Пуассона (1) уравнения (2) и (3), получим
(3)
Слайд 26Подставив в уравнение Пуассона (1) уравнения (2) и (3), получим
Решение этого
Таким образом, потенциал ММ уменьшается с расстоянием по экспоненциальному закону
Решение этого уравнения, учитывающее размер ММ радиусом r, имеет вид
Слайд 28Расстояние Х0, на котором ϕ падает в е раз (ϕ =
Это толщина ионной оболочки которая окружает в электролите каждую заряженную молекулу.
Слайд 29Влияние концентрации ионов на взаимодействие заряженных ММ определяется ионной силой раствора
Тогда толщина ионной оболочки Х0:
Т.е., при большой ионной силе раствора (высокой концентрации соли) оболочка ионов становится меньше (тоньше) и все ионы прижимаются к поверхности ММ
Слайд 31В разбавленных солевых растворах, когда ионная сила небольшая, а дебаевская длина
При высокой ионной силе белок осаждается в растворе и это явление называется высаливанием. Оно используется для экстрагирования и очистки белков.
Слайд 32Дополнение:
При взаимодействии заряженных ММ с дипольными молекулами воды происходит образование гидратных
Чем меньше радиус иона, тем больше его энергия и тем больше молекул воды к нему присоединится. Поэтому самые маленькие ионы при гидратации превращаются в большие гидратированные.
В периодах радиусы уменьшаются (Li → Be → B…) = большая оболочка
В подгруппах радиусы увеличиваются (Li → Na → … → Cs) = малая оболочка
Слайд 33Лекция №2
«Конформация макромолекул. Виды конформационных перестроек»
16 февраля 2017 г. ауд.
13.50